基于弹性FA算法的混凝土罐车自适应液压驱动优化控制
2023-04-29徐珊珊赵娜
徐珊珊 赵娜


摘 要: 混凝土罐车在行驶过程中罐内流体晃动引起的非轴对称问题受到复杂路面对车辆的激励影响,使得流体晃动与车身动态出现耦合。传统的液压驱动比例积分微分(PID) 控制方法在应对此类问题时效果欠佳,容易导致倾覆等事故的发生。为提升液压驱动控制系统的精度和稳定性,该文提出了基于弹性萤火虫(FA)算法的优化粒子滤波器PID自适应控制方法,加速控制参数优化的收敛速度,并分析其液压驱动控制特点和结构上的应用。结果表明:提出的自适应控制方法与传统PID 控制相比,能够显著降低液压驱动控制平均速度误差至0.06 km/h,最大速度误差降至0.29 km/h,同时还提高了控制跟踪性能和稳定性,对混凝土罐车液压驱动控制优化的实际应用具有重要的参考价值。
关键词: 自适应控制;液压驱动;混凝土罐车;弹性萤火虫算法(FA)
中图分类号: U 469.65 ;TD 561 文献标识码: A DOI: 10.3969/j.issn.1674-8484.2023.05. 006
工地是建筑生产的主要场地,也是混凝土罐车的主要作业场所。但工地通常包含大量非铺装地面[1-3],路面情况非常复杂多变,且坡路较多,车辆行驶过程中的安全问题十分突出[4]。针对此类问题,可通过结构改进或控制方法优化予以解决。目前,基于独立悬架前双横臂的混凝土罐车可以适应多变的地形情况,并且具有优良的通过障碍和坡面的性能[5-6]。但上述方案仍不足以解决混凝土罐车在复杂环境下的行驶问题,例如上坡路面和斜坡路面。
混凝土罐车在复杂路面行驶时,罐内流体的晃动会导致非轴对称问题,极大影响车身动态特性。当车辆受到复杂路面激励时,流体晃动与车身动态特性会相互耦合,严重情况下会导致车辆倾覆等事故。因此,对罐车受力情况的分析和控制性能效果的优化至关重要[7-8]。刘妤等[9] 建立了履带车辆软坡地面力学模型,并与RecurDyn 模型进行了对比验证,证明了该力学模型的有效性和准确性。何健等[10] 在Baker 公式的基础上进一步改进了履带车辆软泥路面力学模型,实现了对软土路面上车辆行驶更精确的建模分析。李楠等[11] 针对液压驱动控制中存在的控制误差较大问题,采用优化粒子群方法实现了比例积分微分(proportionalintegral differential,PID)控制参数的在整定,以达到液压驱动精确控制的目标。石瑶等[12] 将自适应控制与粒子群优化模型结合,对比分析了在粒子群优化整定下的控制效果,优化后的控制算法对自适应控制动态特性的改善具有很大的作用。徐正玉等[13] 在非线性系统中采用萤火虫算法(firefly algorithm,FA)进行计算处理,与粒子群算法进行了对比,发现FA 在精度和稳定性方面表现更好。
为了优化混凝土罐车的液压驱动控制,本文采用萤火虫滤波补偿优化自适应控制算法,并加入弹性机制来加速优化过程;建立了混凝土罐车驱动优化控制系统模型,并与传统PID 控制方法进行对比仿真;最后分析了混凝土罐车在软泥坡路运动时采用优化驱动控制的效果。
1 混凝土罐车动力学模型
1.1 混凝土罐车工地软坡行驶力学模型
为研究混凝土罐车在软坡行驶时的运动状态,对车体进行受力分析,如图1 所示,L1,L2,L3 分别表示混凝土罐车质心与前、中、后轮胎与道路坡面接触点间沿斜坡方向的距离,H 为质心垂直与坡面的法向距离。
2.3 利用弹性萤火虫算法(FA)优化PID 参数建立了混凝土罐车静液压驱动系统弹性FA 算法优化滤波自适应PID 控制结构后,接下利用弹性萤火虫算法对PID 参数进行优化,具体的优化步骤如下:
1) 根据工程方法确定PID 控制器中各参数的取值范围kp∈ [0,100],ki∈ [0,1],kd∈ [0,1],选择初始种群规模N = 50, 初始荧光亮度I0 = 5,最优粒子吸引力初始值β = 0.4,最优粒子和随机函数的增益系数α 和β 分别为0.08,0.04,判断半径rjudg = 0.04,高似然粒子的最大比率prmax = 0.95,最大迭代次数为100。
2) 依据2.2 中的粒子吸引力和粒子密度计算进行迭代。
3) 计算是否满足截止条件,若满足截止条件(达到最大迭代次数或高似然粒子的比率大于最大比率prmax)则输出最优解。
通过上述步骤,上面的初始化结果优化过程中在67 步率先达到了高似然粒子的最大比率prmax 超过0.95的截止条件,经弹性FA 算法优化后的PID 参数整定结果: kp = 58.982, ki = 0.629,kd = 0.876。
3 控制仿真系统实验
MATLAB 具备强大的数值仿真能力,在車辆动力学、机械运动学和控制学等研究领域得到了广泛的应用。本文运用MATLAB/Simulink 仿真工具库建立了集成罐车动力学模型、静液压驱动系统模型、软泥坡面模型和弹性FA 算法优化滤波自适应PID 控制器模型的多因素仿真模型,如图5 所示。
在仿真模型的控制器模块中,本文集成了传统PID和弹性机制的FA 算法优化粒子滤波器PID 控制2 种控制算法, 并使用这2 种算法对混凝土罐车身进行稳定控制,其中,弹性FA 算法优化滤波自适应PID 控制机构框图如图4 所示。为验证所提出的弹性FA 优化滤波自适应PID 控制算法的效果,进行了2 种算法的仿真试验。
为验证所提弹性FA 算法优化滤波自适应PID 控制具备限制控制误差,减小控制超调的性能,首先在时间t = 1 s 时给控制器一个幅值为5 km/h 的阶跃速度信号,通过传统PID 控制和弹性FA 算法优化滤波自适应PID 控制进行液压驱动控制,试验结果如图6 所示。
由图6 可知,在阶跃信号下,采用弹性FA 优化滤波自适应PID 控制算法在时间t = 5.4 s 时就能达到稳定运动状态,稳态误差控制在0.01 km/h 以内,且罐车速度无超调,与传统PID 控制相比,稳定时间提前了约1.6 s,速度稳定控制精度提高了约0.03 km/h。仿真证明了所提控制算法的指标相比传统PID 控制算法更好。
同時,为了证明所提弹性FA 算法优化滤波自适应PID 控制策略在软泥坡面行驶时具备较强的鲁棒性,在速度达到稳定后,让罐车驶上角度为30° 的软泥坡面,测试软坡路面的控制效果,仿真数据如图8 所示。
当时间t = 10 s 时,罐车驶上坡度为30° 的软泥坡面;当t = 16 s 时,罐车驶离软泥坡面。经分析图7 可知,当罐车驶上30° 软泥坡面后,采用传统PID 控制策略,罐车的速度受到沿坡面的分重力影响,出现了一定程度的速度下降和约为0.19 km/h 的稳态误差。直到罐车驶离坡道后,稳态误差才逐渐减小,恢复平地行驶状态。而采用具备更强鲁棒性的弹性FA 优化滤波自适应PID 控制算法时,罐车仅在驶上和驶离坡面时产生大小约为0.04 km/h 的瞬态误差,速度误差在非线控制律的控制作用下能迅速收敛,恢复至稳定行驶状态。可见,即使在软泥坡面上,所提算法依然能将罐车速度控制在稳定行驶状态,并能有效保证罐车的速度跟踪控制精度,相较于传统PID 控制,弹性FA 优化滤波自适应PID 控制算法具备更强的鲁棒性。
为了综合对比传统PID 和弹性FA 算法优化滤波自适应PID 控制对罐车液压驱动控制性能,本文在平路和30° 软坡的连续路面进行匀速和加减速行驶控制仿真,并且在在反馈信号中添加白噪声干扰,以验证所提方法在噪声干扰下的鲁棒性。其中,时间t = 70 s 时,罐车驶上坡度为30° 的软泥坡面;当t = 250 s 时,罐车驶离软泥坡面。总仿真时间为350 s,速度误差为ev,罐车行驶速度跟踪、速度跟踪控制误差和扰动观测结果数据分别如图8 所示。
对试验结果进行分析,见图8a 和图8b 所示,采用弹性FA 优化滤波自适应PID 控制算法的罐车速度控制性能更好,超过了传统PID 控制算法。在整个试验中,传统PID 控制算法的平均速度控制误差为0.13 km/h,最大速度误差为0.39 km/h,均方根误差为0.11 ;而弹性FA 优化滤波自适应PID 控制,其平均速度控制误差为0.06 km/h,最大速度误差为0.29 km/h,速度误差均方根为0.09。并且,由图8c 可知,采用FA 算法优化的扰动观测器能准确观测系统扰动,并实现对系统扰动的精准补偿,提高了系统抗干扰能力。因此,优化的控制模型效果比传统PID 控制模型更好。
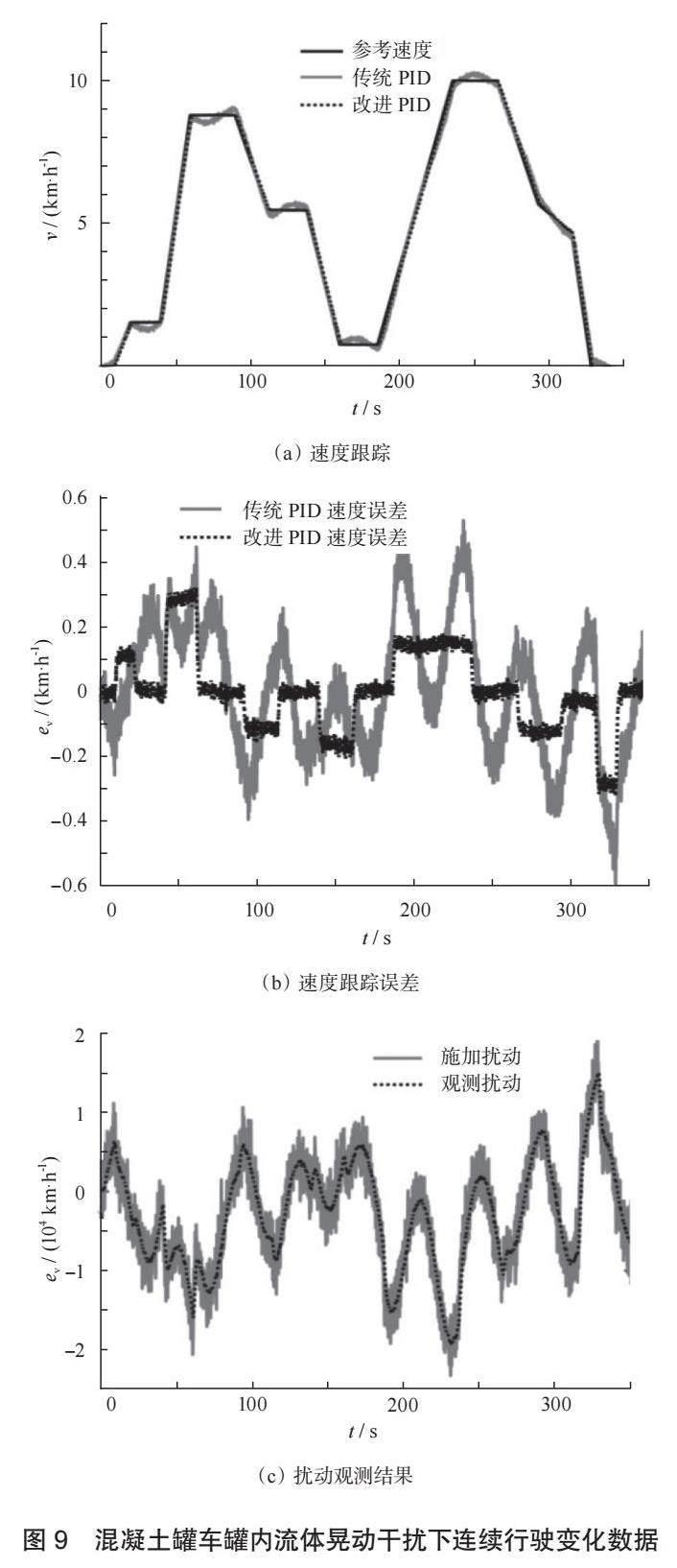
在仿真中加入模拟罐内流体晃动的动态扰动,并在平路和30°软坡的连续路面进行匀速和加减速行驶控制仿真试验,以验证弹性FA 算法优化滤波自适应PID 控制的鲁棒性。罐车行驶跟踪速度、速度跟踪误差和扰动观测结果如图9 中所示。
由图9a 可知,在罐内流体晃动干扰下,采用传统PID 控制方法罐车行驶速度跟踪控制性能明显降低, 尤其在罐车驶入30°(t = 70 s)软泥坡面和驶离30°( t = 250 s) 软泥坡面时段, 速度跟踪误差达0.46 km/h,而采用弹性FA 算法优化滤波自适应PID 控制的罐车速度跟踪误差始终保持在0.3 km/h 以内,如图9b 所示。对比研究表明,采用所提控制方法的混凝土罐车速度跟踪精度与没有干扰情况的跟踪精度基本保持一致,显示了所提控制方法具备更强的鲁棒性。这主要得益所提控制方法一方面能通过弹性FA算法优化机制自动PID 控制参数,适应各工况实现高精度速度跟踪控制行驶的能力更强;另一方面采用扰动观测器能实现系统扰动的在线补偿( 观测结果如图9c所示),进一步提高了系统的抗扰能力。
5 结 论
通过建立混凝土罐车在复杂路面行驶的地面力学模型和静液压驱动系统模型,本研究充分考虑了沉陷量对混凝土罐车受力情况的影响,使研究结果更符合实际作业情况;为了提升控制算法的性能,本文提出了一种集合扰动观测器和标称模型滤波补偿后基于弹性萤火虫(FA) 算法优化滤波自适应PID 控制算法,并使用MATLAB 建立混凝土罐车多因素仿真模型,在阶跃信号、软泥坡道和变速情况下进行仿真。仿真结果表明:提出的弹性FA 算法优化滤波自适应PID 控制算法对混凝土罐车速度控制具有较好的效果,所提算法比传统PID 稳定时间减小1.6 s,稳态精度提高约0.03km/h ;同时30° 软泥坡面加减速鲁棒实验得到,即使在流体晃动、白噪声干扰下,所提自适应PID 控制方法依然能将速度误差控制在0.29 km/h 以内,比传统PID减小0.1 km/h,证明了其有效性。
研究结果表明,与传统PID 控制相比,所提出的弹性FA 优化滤波自适应PID 控制算法对混凝土罐车进行速度控制能够显著提高行驶控制效果,对混凝土罐车的生产和控制具有参考价值并提供有效的支持。
参考文献(References)
[1] 胡素云, 王窈惠, 宋友发. 混凝土搅拌运输车行驶稳定性分析[J]. 筑路机械与施工机械化, 2010, 27(11): 78-81.
HU Suyun, WANG Yaohui, SONG Youfa. Stabilityanalysis of concrete mixing transport vehicle driving [J].Road Mach Construct Mech, 2010, 27(11): 78-81. (inChinese)
[2] 何烈云, 刘强. 非满载液罐车侧倾稳定性的准静态等效力学模型[J]. 力学与实践, 2020, 42(3): 294-299.
HE Lieyun, LIU Qiang. A quasi-static equivalentmechanical model for roll stability of partially-filledtanker trucks [J]. Mech Engineering, 2020, 42(3): 294-299. (in Chinese)
[3] 李显生, 孟祥雨, 郑雪莲, 等. 非满载罐体内液体冲击动力学特性[J]. 吉林大学学报( 工学), 2017, 47(3): 737-743.
LI Xiansheng, MENG Xiangyu, ZHENG Xuelian,et al.Dynamic characteristics of liquid sloshing in partiallyfilledtank [J]. J Jilin Univ (Engi Tech Edit), 2017, 47(3):737-743. (in Chinese)
[4] 崔希海, 朱爱香. JC3型防爆柴油机混凝土罐车的研制[J].矿山机械, 2015, 43(1): 28-30.
CUI Xihai, ZHU Aixiang. Development on JC3 concretemixer truck with flameproof diesel engine [J]. MiningProcess Equip, 2015, 43(1): 28-30. (in Chinese)
[5] 许文超, 成云海, 赵国金. 矿用混凝土搅拌运输罐车关键部件设计与分析[J]. 山东理工大学学报( 自然科学版),2016, 30(5): 7-11.
XU Winchao, CHENG Yunhai, ZHAO Guojin. Designand analysis of key components of mining concrete mixingand transporting tanker [J]. J Shandong Univ Tech (NatuSci Edit), 2016, 30(5): 7-11. (in Chinese)
[6] 卢玫. 槽罐车事故成因分析与安全防范[J]. 中国公安大学学报( 自然科学版), 2020(4): 42-47.
LU Mei. Analysis of the causes of tanker truck accidentsand safety prevention [J]. J China Pub Sec Univ (NatuSci Edit), 2020(4): 42-47. (in Chinese)
[7] 庄继德. 计算汽车地面力学[M]. 北京: 机械工业出版社,2008: 30-40.
ZHUANG Jide. Computational Vehicle Ground Mechanics[M]. Beijing: Machinery Industry Press, 2008: 30-40. (inChinese)
[8] 胡晓明, 李万莉, 孙丽. 液体晃动降低半挂液罐车行驶稳定性[J]. 农业工程学报, 2013, 29(6): 49-58.
HU Xiaoming, LI Wangli, SUN Li. Liquid swayingreduces driving stability of semi-trailer liquid tankers [J].J Agri Engi, 2013, 29(6): 49-58. (in Chinese)
[9] 刘妤. 履带车辆软坡地面力学建模及行驶性能分析[J].机械设计, 2021, 38(3): 110-118.
LIU Yu. Mechanical modeling and driving performanceanalysis of crawler vehicles on soft slope ground [J]. MachDesi, 2021, 38(3): 110-118. (in Chinese)
[10] 何健. 基于改进土壤承压模型的履带车辆行驶振动特性仿真研究[J]. 振动与冲击, 2020(39): 57-77.
HE Jian. Simulation study of driving vibrationcharacteristics of tracked vehicles based on improvedsoil bearing model [J]. Vibr Shock, 2020(39): 57-77. (inChinese)
[11] 李楠. 基于改进PSO 的起重机双马达同步模糊PID 控制研究[J]. 机电工程, 2022, 39(5): 700-704+712.
LI Nan. Synchronous fuzzy PID control of crane doublemotorsbased on improved PSO [J]. J Mech Elect Engi,2022, 39(5): 700-704+712. (in Chinese)
[12] 石瑶, 陈美玲, 张云, 等. 粒子群优化的磁轴承自适应反演滑模控制[J]. 机械设计与制造, 2021(11): 37-41+47.
SHI Yao,CHEN Meiling,ZHANG Yun,et al.Application of adaptive backstepping sliding modecontrol based on particle swarm optimization in magneticbearings [J]. Mach Desi Manufact, 2021(11): 37-41+47. (inChinese)
[13] 徐正玉, 付能翼, 周洁, 等. 瞬变电磁法非线性优化反演算法对比[J]. 吉林大学学报( 地球科学版), 2022, 52(3):744-753.
XU Zhengyu,FU Nengyi,ZHOU Jie,et al. Comparisonof nonlinear optimization inversion algorithms of transientelectromagnete [J]. J Jilin Univ (Earth Sci Edit), 2022,52(3): 744-753. (in Chinese)
[14] 周如意, 丰文浩, 邓宗全, 等. 轮地力学模型参数灵敏度分析与主参数估计[J]. 航空学报, 2021, 42(1): 253-265.
ZHOU Ruyi, FENG Wenhao, DENG Zongquan, et al.Sensitivity analysis and dominant parameter estimationof wheel-terrain interaction model [J]. Acta AeronautAstronaut Sinica, 2021, 42(1): 253-265. (in Chinese)
[15] 曹洁, 王振莹, 李伟. 抗遮挡的鸡群优化粒子滤波目标跟踪方法[J]. 微電子学与计算机, 2019, 36(6): 40-44.
CAO Jie, WANG Zhenying, LI Wei. Anti-occlusionparticle filter target tracking method based on chickenswarm optimization [J]. Microelect Comput, 2019, 36(6):40-44. (in Chinese)
