基于二进制粒子群优化算法的封装式特征选择研究

周晶喆 侯能 宋成龙

关键词： 封装式特征选择；二元粒子群优化算法；转换函数；预测准确率

0 引言

在机器学习和数据挖掘中，特征选择是一种重要的数据预处理手段技术。所谓特征选择，指从原始数据集的特征集合中，通过设计算法，找到一组特征子集，该特征子集能使给定机器学习模型的评价指标到达最优[1]。

根据流程的不同，特征选择分为过滤式、嵌入式和封装式[2]。3种特征选择各有其优势和局限性，本文主要讨论封装式特征选择。封装式特征选择方法常用在监督学习中，由目标学习算法和搜索策略两部分构成。其中，目标学习算法用于评判特征子集的优劣。而搜索策略关注如何高效地从所有特征子集中找到使监督学习算性能最优的子集。假设一个数据集的样本由N个特征组成。根据每个特征的选择与否，可能的所有特征子集组合数有2N个。封装式特征选择中就是通过设计搜索算法，从所有的2N个可能组合中，找到最优特征组合。

已有文献指出，封装式特征选择是一种NP难问题[3]。求解该问题的搜索方法包括穷举法、启发法和群体智能算法。其中，穷举法需要评价所有的候选方案，不适合特征数较多的数据集；启发式方法虽然能高效地得到近似解，但解的质量离最优解差距较大；群体智能算法是目前求解该问题的常用方法[4-5]。然而，群体智能算法在提出时，主要用于求解连续的函数优化问题，解的表达在每个维度上是浮点数。本问题中，解的表达只有0和1两种取值。当使用群体智能算法方法求解特征选择时，需要考虑将解的表达离散化后，原始算法仍然能够在二元离散问题中起作用。

因此，本文以经典的粒子群优化算法作为起点，探索了二元粒子群优化算法中的不同转换函数对求解质量的影响。在实验阶段，通过在不同的数据集上进行测试，分析了二元粒子群算法在特征选择问题中的性能表现。

1 提出方法

1.1 标准粒子群算法

标准的粒子群优化算法（Particle Swarm Optimiza⁃tion， PSO）最初由Kennedy和Eberhart于1996年提出的一种群体智能算法[6]。算法用多个粒子模拟鸟群的社会行为的方式寻找最优解。在搜索空间中，粒子以迭代的方式四处飞行。寻优时，每个粒子会更新各自的寻优轨迹。不仅如此，粒子在移到下一个位置时，既考虑自身已有的最佳解，也要考虑种群其他粒子已找到的最佳解。最终，整个种群找到全局最佳解。

PSO中，每个粒子在寻优中更新各自的位置时，要考虑自身的当前位置、当前速度、自身的历史最佳位置、全局最佳位置。更新位置的过程可形式化描述为如下两式：

以上两式中，xit和vit分别表示第t 次迭代时，第i 个粒子的位置和速度；pbesti表示第i 个粒子在第t 次迭代时已知的个体历史最优位置；gbest表示在第t次迭代时，各个粒子找到的已知全局最佳位置；r1和r2表示[0，1]之间的随机数；c1和c2都表示加速度系数，通常取固定值2.0；w 表示第t 次迭代时粒子的速度惯性系数，取0.4～0.9之间的数。w 取值越大，粒子探索全局最优的能力越强，但是随着迭代的进行，有可能跳过全局最优解；xit+1和vit+1分别表示在第t+1 次迭代时，粒子更新后的位置和速度。

从以上两式可看出，粒子的位置更新公式（2）取决于速度更新公式（1）的3个部分，即当前速度、自身历史最佳位置与自身位置的距离、全局最佳位置与自身位置距离的合成。位置和速度一般都表示为向量，以上两式作用在向量的每个分量上。

总体来说，用PSO优化待解决的问题时，首先将粒子位置进行随机初始化，速度初始化为0；然后，初始化每个粒子的个体最佳历史位置，根据每个粒子的适应度值初始化全局最佳位置；在每次迭代时，每个粒子使用公式（1）和（2）更新速度和位置、更新历史最佳位置；最后，根據所有粒子的更新位置更新全局最佳位置。迭代过程重复执行，直到迭代次数满足预先设置的次数为止。

1.2 二进制粒子群算法

标准的PSO适用于求解连续空间的优化问题，即每个粒子的位置分量都是定义域范围内的实数；现实生活中，大多数问题都被建模为组合优化问题，即问题的解分量是离散的。典型的组合优化问题有两种解形式：解分量只有0和1两种状态的（01背包问题、特征选择问题）和解分量为从一组数字中无放回取样的（旅行商问题、流水车间调度问题）。对于离散空间的寻优，标准PSO算法无法直接使用。因此，根据标准PSO的原理，Kennedy和Eberhart于1997年进一步提出粒子位置分量只有0和1两种状态的二元粒子群优化算法（Binary Particle Swarm Optimization， BPSO）[7]。对于BPSO，可以将位置空间的所有状态看成是一种超立方体。单个粒子表示超立方体的某一个角点，搜索使粒子在超立方体的角点间移动。尽管BPSO中粒子的位置分量只有0和1两种值，粒子的速度更新公式（1）仍然适用，其结果也仍然是实数。

BPSO与标准PSO的另一个区别在于BPSO舍弃了位置更新公式（2），改用sigmoid转换函数将得到的实数型速度分量值转换到[0，1]区间。然后，用一个随机数与转换后的值进行比较。如果随机数比转换后的值小，意味着随机数位于sigmoid内，位置分量设置为0；否则，随机数位于sigmoid外部，设置为1。将位置转换形式化为如下：

1.3 转换函数

自BPSO 提出后，有一些研究工作提出不同的BPSO算法和原始的BPSO进行比较。这些工作中，文献[8]重点研究了转换函数并总结了S类和V类两大类，共8个转换函数。在实验阶段，对这8个转换函数进行了对比分析。此外，对于粒子的速度更新公式（2）中的系数w，改为迭代中在[0.4， 0.9]范围内线性递减。

在特征选择问题中，除了BPSO外，使用其他群体智能算法求解该问题时也需要用到转换函数。同时，S类和V类两大类转换函数中，s2和v2是该问题中是经常选用的函数，这两种转换函数不需要对定义域设置上下界。然而算法在实际执行时，每个粒子会在更新速度后进行上下界判断，使速度限制在上下界中。当定义域存在上下界时，转换函数除了s1和s2外，也可以是线性的。线性转换函数的表达式如下：

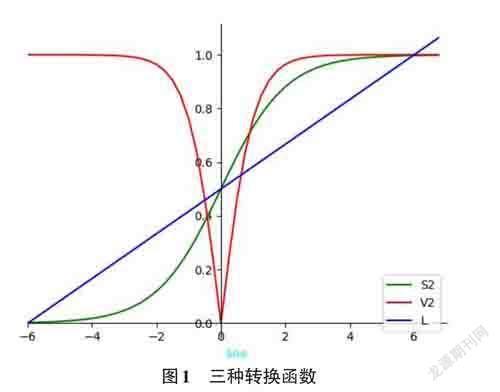
上式中，vmax、vmin分别为速度的上下界。s2、v2和线性转换函数的对比如图1所示：

从图1中可以看出，三种转换函数在图中覆盖区域大小是不同的。这意味着，相同的速度分量，由于转换后的概率值不同，使得产生的随机数被转换为1还是0的结果有所区别，从而影响特征的选择与否。

1.4 适应度函数

本文中，封装式特征选择的目标函数形式化为最小化优化问题：

上式的优化目标由两部分组成，一是监督学习算法的性能，二是被选择的特征数量。具体地，给定数据集S，每个样本的特征数为M，Accuracy（S）表示目标监督学习算法在数据集S上的预测准确率。相应地，1-Accuracy（S）表示目标监督算法的错误率。错误率越低，算法的预测能力越强。第二部分中，m 表示被选择特征的个数，M 为样本数据的全部特征总数，m/M表示选中的特征数量占总特征数量的比重。这两个部分通过权值ɑ调节两个目标的重要程度。本文中，根据文献[9]的建议，ɑ取值0.99。

1.5 粒子表达

BPSO中，每个粒子在每个维度上的取值只有0和1两种，这种表达方式和特征选择问题天然地吻合。粒子的维度等于样本的特征数量，每个维度分量取值为0或者1表明即对应样本特征分量的选择与否。这意味着一个粒子就代表了一种特征选择方案，一种选择方案就对应一个目标函数值，即公式（6）的结果。

2 实验

为了测试BPSO算法求解封装式特征选择问题的性能，本文选用了UC Irvine Machine Learning Reposi⁃tory中的部分数据集。这些数据集在样本、特征以及类别数量上都各不相同。所选数据集的具体参数如表1所示：

实验的软硬件环境为：CPU型号为Intel（R） Core（TM） i5-1035G1，内存大小为8GB，操作系统为WIN10。算法采用Python3 实现，且选用numpy，sklearn第三方库。二进制粒子群算法涉及参数设置为：个体数量为12，维度大小取决于选用的数据集，进化代数为50。

封装式特征选择问题中，通常会用KNN作为监督学习算法来评价提出的搜索算法的性能。KNN无须对样本进行训练，在测试阶段直接计算测试样本和所有训练样本的距离，以距离训练样本的远近程度来预测测试样本所属类别。对于KNN，本文调用sklearn库实现，且采用默认参数（邻域k=5，欧式距离计算样本间的相似度）。

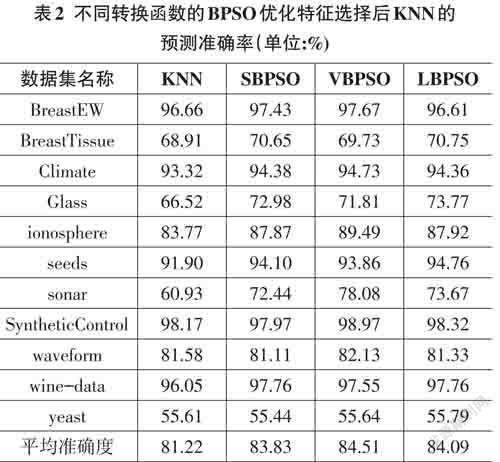
为了更好地评价不同转换函数在本问题中的表现，本文测试了三个代表性的转换函数，即1.3节所述的S2、V2和线性转换函数。三种转换函数对应的BPSO分别命名为SBPSO、VBPSO和LBPSO。三种BPSO在所有数据集上的运行结果如表2所示：

表2中，第1列为数据集名称；第2列表示不采用特征选择，即所有特征都用于监督学习时，KNN的预测准确率；第3列～第5列分别是采用三种转换函数的BPSO优化特征组合方案后，KNN的预测准确率；最后一行表示根据所有数据集的预测结果计算平均值。

与第2列的完全不使用特征选择方案相比，比较突出的结果总结如下：

在Sonar数据集上，SBPSO能将KNN的预测准确率能提高11.51%；VBPSO能够将KNN的预测准确率能提高17.15%；LBPSO能够将KNN的预测准确率能提高12.74%。

在Glass数据集上，SBPSO能将KNN的预测准确率能提高6.46%；VBPSO能够将KNN的预测准确率能提高5.29%；LBPSO能够将KNN的预测准确率能提高7.25%。

在Seed数据集上，SBPSO能将KNN的预测准确率能提高2.2%；VBPSO能够将KNN的预测准确率能提高1.96%；LBPSO能够将KNN的预测准确率能提高2.86%。

在其他数据集上，三种BPSO算法也能不同程度地提高KNN的预测准确率，这也说明了封装式特征选择对于提高监督学习算法性能的有效性。如表2的最后一行所示，通过在所有选定数据集上计算平均值，使用V2转换函数的VBPSO的性能是最好的，即能够将KNN的预测性能平均提升3.29%。

3 结论

本文对二进制粒子群优化算法用于封装式特征选择问题时，不同的转换函数对算法性能的影响展开了研究。在11个数据集上测试了三种转换函数的性能。实验结果表明，采用V2型转换函数的二进制粒子群优化算法，对KNN的预测准确率的提升，在總体上表现是最好的。在今后使用更新的群体智能算法求解特征选择时，将就如何对算法进行二元化展开研究。