三角质心迭代与Bounding-Box的定位算法

程良 张永强 王艳娥 司海峰 李璐

关键词：无线传感器网络；PIT法则；估计矩形；质心迭代

无线传感器网络作为一个应用广泛的技术，具有自组网、健壮性强等特点，备受研究者们关注[1]。现阶段的定位算法主要分为两类：基于测距以及非测距[2]。相比测距算法，非测距算法具有通信开销小、功耗低等优点，得到了广大研究人员的认可，是现阶段研究工作的重点之一[3]。

现阶段较为流行且先进的无线传感器网络定位算法有以下几种。文献[4]对边界盒定位算法进行了改进，该算法主要是通过缩小定位区域来提高精度；文献[5]综合测距与非测距定位算法的特点进行定位，根据RSSI值来计算相关权重来提高定位精度。文献[6]找出锚节点组成的三角形中最小的那一个作为阈值三角形，来进一步确定为未知节点坐标。文献[7]采用极限分割的思想，将Bounding-box算法中形成的估计矩形进行了无限次分割来提高定位精度。本文通过分析基本Bounding-Box 算法原理，将原始矩形进行一次分割后，采用三角质心迭代的方式来极限逼近未知节点，从而减小了平均相对定位误差，提高了定位准确度。

1 Bounding-Box 算法简介

Bounding-Box 算法的基本工作原理：在一个二维区域内，待定位节点接收到周围最近三个锚节点的信号强度，然后以该锚节点为圆心，通信距离为半径画圆，同时将三个圆的外接矩形求出，以它们重合区域的质心作为未知节点的位置[8]，可将该算法分为3个步骤。

1） 在一个二维平面内，随机布置多个锚节点和未知节点，锚节点将自身的位置信息广播至整个网络。在该网络中，锚节点发送的信号能被未知节点接收到的称为最近锚节点。

2） 以未知节点周围锚节点为圆心，它们的通信距离为半径画圆，得到圆的外切正方形。

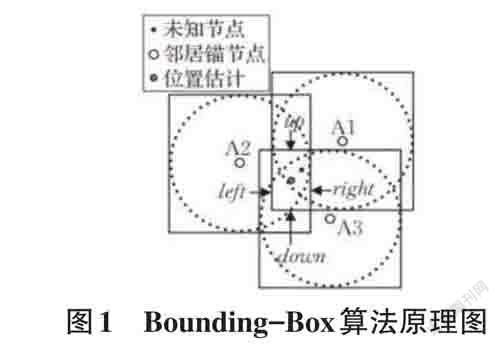
3） 将第二步得到的各外接矩形的重合區域作为初步定位区域，即初步未知节点的预估位置为该重合区域的中心位置。如图1所示，外接矩形的重叠部分区域是一个平行X 轴和Y 轴的矩形，分别将该矩形的左、右、上、下四个边记为left、right、up以及down，并且求出该重合矩形的中心位置，以此作为最终估计位置。

2 算法改进

分析Bounding-box算法可知，只通过邻居锚节点所得到的外切正方形重合区域质心作为未知节点的位置估计会造成较大误差。文中采用分割的思想，将定位区域逐渐缩小，从而降低算法的平均相对定位误差。

改进过程可分为三步：

第一步：估计初始位置坐标

通过定位算法求解的外切正方形所形成的重合矩形可作为初步的定位区域，求出该区域的中心点位置坐标（x0，y0 ），将该坐标作为初步的定位位置。

第二步：找到最近锚节点

对未知节点接收到周围锚节点的信号强度值进行标记：

第三步：三角形质心迭代

1） 一次分割

Bounding-Box算法得到的最初估计区域是根据最近锚节点画通信圆，每个圆的外接矩形形成的重合矩形部分为最初定位区域。将该定位区域的中心位置坐标记为（x0，y0 ），以该坐标为中心，将该重合矩形分成四个子矩形，分别记为B1、B2、B3 、B4且大小分别为式（3）～式（6）。

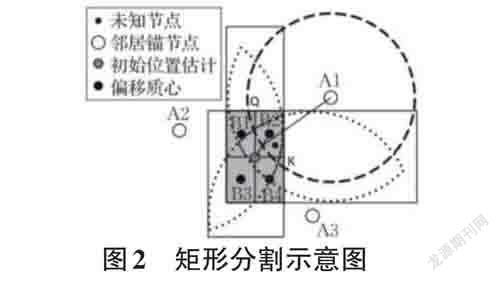
如图2所示，其中（xi，yi ）分别作为邻居锚节点的坐标位置，R为通信半径。由四个子矩形得到的质心称为偏移质心（xes，yes ），其中s 下标代表的是不同的子矩形。采用两点距离公式求出偏移质心到最近锚节点的距离，设为dist，如式（7）所示：

找出最近距离min（dist），假设B2子矩形的质心到最近锚节点A1最近，将B2的质心（xe2，ye2 ）称为待选质心。求初始位置坐标和待选质心的中点坐标GS1为（xs1，ys1 ），再计算该中点坐标到最近锚节点的距离dis，并且以A1为圆心，dis 为半径画圆，交估计矩形于Q，K 两点。将距离dis 带入式（8）求出对应的信号强度RSS （dis），比较RSS （dis） 与max（RSS） 大小关系，若RSS （dis）

2） PIT法则

对于WSN的拓扑网络，各节点都属于静止状态，所以不能采用PIT法则进行未知节点位置的判断。为了达到实验效果，采用近似PIT的方法，因为未知节点和锚节点之间可以进行信号强度的接收，所以利用这种信号强度随距离变化的关系就可以模拟未知节点的运动情况，进而对未知节点的位置进行判断。

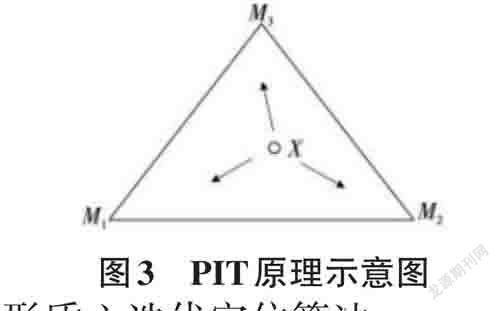
由于未知节点可以探测到周围锚节点的信号强度大小，所以可以读出三个邻居节点M1，M2，M3的信号强度值。假设X 运动到其中一点，就可以认为未知节点的信号强度变成了该点的信号强度，从而判断出移动的过程中未知节点与三个顶点间信号强度的变化关系，同理远离也一样，进而就可以判断出未知节点是否在三角形M1，M2，M3中。

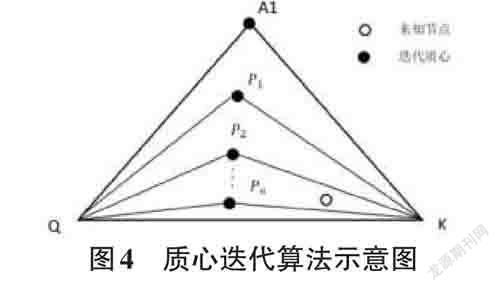
一次分割完成后，以最近锚节点A1 为圆心，A1 到GS1 为半径画圆，得到与B2区域的两个焦点设为Q，K，连接Q，K，A1 构成三角形。通过PIT法则判断，如果未知节点在三角形内部，则求其质心P1，否则以Q，K，P1为三个顶点组成新的三角形继续迭代，直到未知节点不在三角形Q，K，Pn内部，迭代终止。算法流程如下：

步骤1：计算未知节点到Q，K，P1，P2...Pn的距离

如果在一个二维区域内，存在一个未知节点O（x，y ），它周围的邻居锚节点分别为A1，A2...An，设第n 个信标节点的坐标为（xn，yn ），则未知节点到邻居锚节点距离dn为：

通过两点间距离公式可得质心坐标到未知节点的距离，记为ds。

因此，由公式推导可得：若知道dn，则可以求出未知节点O 到质心S的距离ds。以质心S 为圆心，ds 为半径作一个圆MO 的方程。过质心S 分别与Q 和K 连接形成的直线交于圆MO，设交点坐标分别为U 和V，将QU 与KV 之间的距离近似当作Q到未知节点和K到未知节点的距离。

步骤2：三角形质心迭代定位

进行三角形质心迭代定位之前，要先确定未知节点是否在相应的三角形内。由步骤1知道未知节点分别到Q、K的距离后，利用PIT法则判断出未知节点是否处于三角形A1，Q，K 内，因为Q，K 处于未知节点和最近锚节点形成的同心圆内，所以将Q，K 固定不变并且与质心P1 形成新的三角形，然后通过PIT法则判断。若未知节点在三角形QKP1 内，则继续进行迭代运算，直到未知节点不在新构成的三角形Q，K，Pn 内，否则算法迭代终止。

设未知节点到Q，K，P1，P2...Pn的距离为d3。

找出d3 中最小的距离记为min（d3 ），则对应的质心为最终位置估计。随着迭代次数的增加，若未知节点处于Q，K 所构成的直线附近，那么会有无限次的迭代，因此需要设置迭代阈值。

设dpn 与通信半径r 的比值为误差ξ，如果ξ 小于设定阈值，则迭代终止，如式（16）所示。

3 仿真实验

3.1 实验设计

该实验利用Matlab 为仿真工具，来模拟仿真这几种算法分别在不同环境下的平均定位误差精度。文中新设计的算法记作TCIBounding - Box 算法，文献[4-7]中所提到的定位算法分别记为RBounding - Box、RSSI - Centroid、APIT - Minimum 以及DBounding - Box。監测区域设计为100m × 100m，其中设节点数个数为N，锚节点的个数为M，节点通信半径为R，其中设PT=0dB，d0=1m，PT（d0）=55dB，ƞ=4，ξ=0.1。设网络中定位算法的平均相对定位误差为E，计算公式如式（17）。

其中（xr，yr）是未知节点的估计坐标，（xt，yt）是未知节点的真实坐标，k为拓扑次数，nr 参与定位的未知节点个数。

为了使实验结果更具有说服性，将每次实验产生的拓扑场景分别提供给以上算法进行对比。

3.2 节点数对定位精度的影响

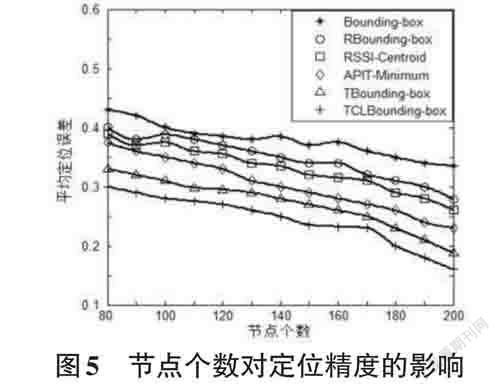
节点总数是衡量一个拓扑网络整体性能的重要参数，节点过多会提高成本，锚节点过少会影响实验精度。因此，本实验设锚节点数为0.2N，通信半径为30m，仿真结果如图5所示。

分析图5可得，随着节点数越来越多，TCIBounding- Box 算法相比于传统算法、RBounding - Box、RSSI - Centroid、APIT - Minimum 以及DBounding - Box 算法的定位误差分别降低了14.12%，6.72%，5.09%，3.53% 以及2.68%。

3.3 锚节点数的影响

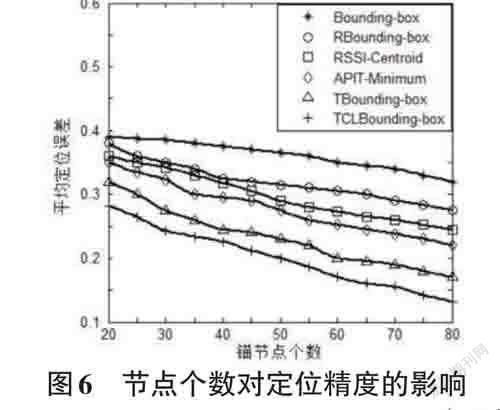
锚节点作为整个WSN网络位置信息的参考点，数量决定着定位精度。实验中设N为100，R为30m，k= 100次。如图6是锚节点数量从20增至80的仿真图。

由图6可得，锚节点越多，算法的平均定位误差越小。文中TCIBounding-Box 分别较传统算法，文献[4-7]提到的算法，在平均定位误差上分别降低了6.19%，5.42%，4.22%，3.77%以及2.68%。

3.4 通信半径对定位精度的影响

由分析得，通信半径对外接矩形区域大小有影响。如果通信半径距离过小，会导致部分节点不能参与定位。实验中节点个数和锚节点个数按照一定比例投放，保证其他条件都不变的情况下，通信半径对实验的影响。图7为仿真图。

分析图7可知，文中提出的TCIBounding-Box 算法相比于传统的算法在平均定位误差上减少15.42%。文献[4]中的算法在平均定位误差上相比于传统算法有所降低，但与文中所提算法相比，定位精度降低了7.15%。文献[5]中的定位算法，在精度上与文中所提算法相比降低了5.25%。文献[6]中的算法降低了3.60%。文献[7]中的算法降低了2.66%。

4 结束语

本文先对Bounding-Box算法进行了研究分析，并在该基础上利用最近锚节点将产生的外接矩形区域进行一次分割，以此进一步缩小定位区域。通过判断未知节点是否在最近锚节点的通信圆内，对定位区域进一步缩小，然后通过三角形质心迭代思路不断缩小定位区域。仿真实验表明，在不同节点个数，锚节点个数以及通信半径下，本文所提出的TCIBounding- Box算法均有效减小了平均定位误差。