反映博物馆展柜瞬态环境温度变化的三维CFD建模与分析

何 纳,唐 欢,袁 泉,赵 卓,曾 檀

(重庆中国三峡博物馆,重庆 400015)

0 引 言

温湿度是评价馆藏文物保存环境的重要因素[1-2]。文物保存微环境温湿度的监控是文物预防性保护工作的重要内容[3]。各博物馆长期以来的温湿度监测已产生大量的文物保存微环境实测数据[4-6]。如何更好地处理、分析并利用现有数据,从中挖掘出更大的价值,是当前文物预防性保护领域的研究热点[7-9]。因此,如果能利用现有的监测数据建立有效的数学分析模型,用以评估并优化现有的文物保存微环境调控措施,将具有很大的现实意义。

计算流体力学(computational fluid dynamics,CFD)是一种细致描述流体行为的计算机仿真建模工具,在模拟流体流动、传热-传质过程等方面有广泛的应用[10-12]。近年来,有研究者开始尝试将CFD应用于文物保存微环境的研究中,如Delia等[13-14]通过CFD建立了稳态边界条件下,保存文物的古建筑内空气流动-传热的模型;王丽娜等[15]通过CFD对展柜进行稳态建模,模拟了不同送风量对展柜内气流分布的影响;刘斌等[16]应用CFD建立了稳态温度边界条件下展柜内温度变化的模型。以上研究证明CFD可被应用于包括博物馆展柜在内的文物保存微环境内温度、流场分布的数学建模,并探索、优化文物保存微环境的控制策略。

上述研究均采用稳态边界条件进行建模,本研究在此基础上,采用瞬态温度边界建模方法,建立能反应展柜所处环境温度实际变化的瞬态三维CFD模型,并利用博物馆实测温度数据[17]进行模型标定,在有效利用监测数据的同时提高了模型的可靠性。具体来说,重点讨论以下几个要点:1)建立可反应展柜所处环境温度瞬态变化的三维CFD仿真模型;2)利用夏季工况实测数据标定模型,并将模型直接应用于冬季工况,以进一步验证模型精度;3)实现瞬态环境温度变化条件下,展柜内温度场、空气流场分布的可视化。

1 实验设计

1.1 研究对象

重庆中国三峡博物馆位于重庆市渝中区,博物馆展厅共四层,本工作选取展厅二层某独立展柜开展研究(图1)。该展柜内无通风换气设备,柜内温度由展厅集中式中央空调调控,通常展厅中央空调系统的开启和关闭时间分别为09∶00和16∶45。

图1 展柜照片

1.2 监测仪器及数据获取

本研究使用两套SWJ-T/H1-1.1型温湿度记录仪对展厅及展柜内温度数据进行监测与记录。仪器的温度测量范围为-30～70 ℃;显示分辨率:0.01 ℃;在15～30 ℃之间,测量精度在±0.3 ℃以内。监测过程中,展厅与展柜内温度数据的采样间隔分别为15 min和10 min。考虑到重庆地区夏、冬两季气候条件的特殊性,本研究选取了夏/冬季工况下两组典型的展柜内-外实测温度数据进行建模与分析,数据选取时间为:2019年8月5日、2019年1月21日。

2 数值模拟

2.1 几何建模

该立式展柜的尺寸为0.6 m×0.6 m×0.85 m,展柜底部铺有一层绝热材料,柜体除底面外,其余五面均为透明有机玻璃制成,如图1所示。依据上述实际尺寸,建立了该展柜的三维几何数模,如图2所示。

图2 展柜三维数模

2.2 物理-数学模型

展柜内气体流动由三维Navier-Stokes方程组(质量守恒方程、动量守恒方程、能量守恒方程)描述。湍流建模选取标准k-ε模型,近壁区流体运动采用标准壁面函数法,离散格式为二阶迎风格式,采用基于速度-压力耦合模型的SIMPLE算法求解。展柜内空气低速流动,因此以不可压缩流体模型描述。模型的控制方程包括连续性方程、动量守恒方程、能量守恒方程、k(湍动能)方程和ε(耗散率)方程,如式(1)～(5)所示。

1) 连续性方程

(1)

2) 动量守恒方程

(2)

3) 能量守恒方程

(3)

4) 标准k-ε方程

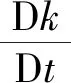
(4)

(5)

式中,k为湍流动能;Pk表示湍流动能k的平均速度梯度引起的生产项;Gk表示湍流动能k的浮力生产项;Dk表示湍流动能k的扩散项;ε为湍流动能k的耗散率;Dε为耗散率ε的扩散项;Cε1、Cε2、Cε3为模型常数,Cε1=1.44,Cε2=1.92,Cε3=0.09。

2.3 边界条件及网格划分

展柜6个表面均设为壁面边界,其中底面采用绝热边界条件,其余5面采用对流换热边界条件,其中对流换热系数由文献值给定[16],环境温度由瞬态实测数据给定。具体来说,将实际测得的24 h展柜外环境温度数据用C语言编写为UDF文件,并编译导入CFD软件中,作为五个对流换热面的瞬态温度边界条件。此五面的有机玻璃厚度由壳层模型(Shell model)进行描述,壳层厚度由实测厚度给定,玻璃导热系数的初始值参照普通玻璃物性,由文献给定,在后续夏季工况的模型标定中作为可调参数,由模型的标定过程最终确定。

网格由六面体组成。为消除网格尺寸对结果造成的影响,本研究建立了不同尺寸的三个网格模型,分别为M1、M2、M3,其单元尺寸依次减小,网格密度依次加大,网格参数见表1。

表1 网格参数设定

对三种不同尺寸的网格进行运算求解,结果如图3所示。不同网格尺寸对计算结果的影响可忽略不计,当网格达到M1的尺寸时,已能满足模拟计算精度的要求,若选择更加精细的网格,将会增加计算时长,故选用网格为M1。

图3 不同网格尺寸对展柜内部温度模拟结果的影响

2.4 瞬态仿真设置

此瞬态模型采用的时间步长为60 s,内迭代次数为20次,单次瞬态分析总物理时间为86 400 s(24 h)。为了将CFD瞬态模拟产生的数据用于后续分析,计算过程中将以10 min为间隔实时保存柜内温度数据,并生成文本文件。

3 结果与讨论

3.1 传热过程分析

传热过程有热传导、热对流与热辐射三种,本研究中展柜模型所涉及的主要有两种,即热对流与热传导。具体来说,玻璃内部的传热方式为热传导,玻璃内壁面与内部空气、外壁面与外部空气之间为热对流。为了更清晰地描述展柜传热过程,这里将其在一小段时间内简化为拟稳态的一维传热过程加以说明,如图4所示。

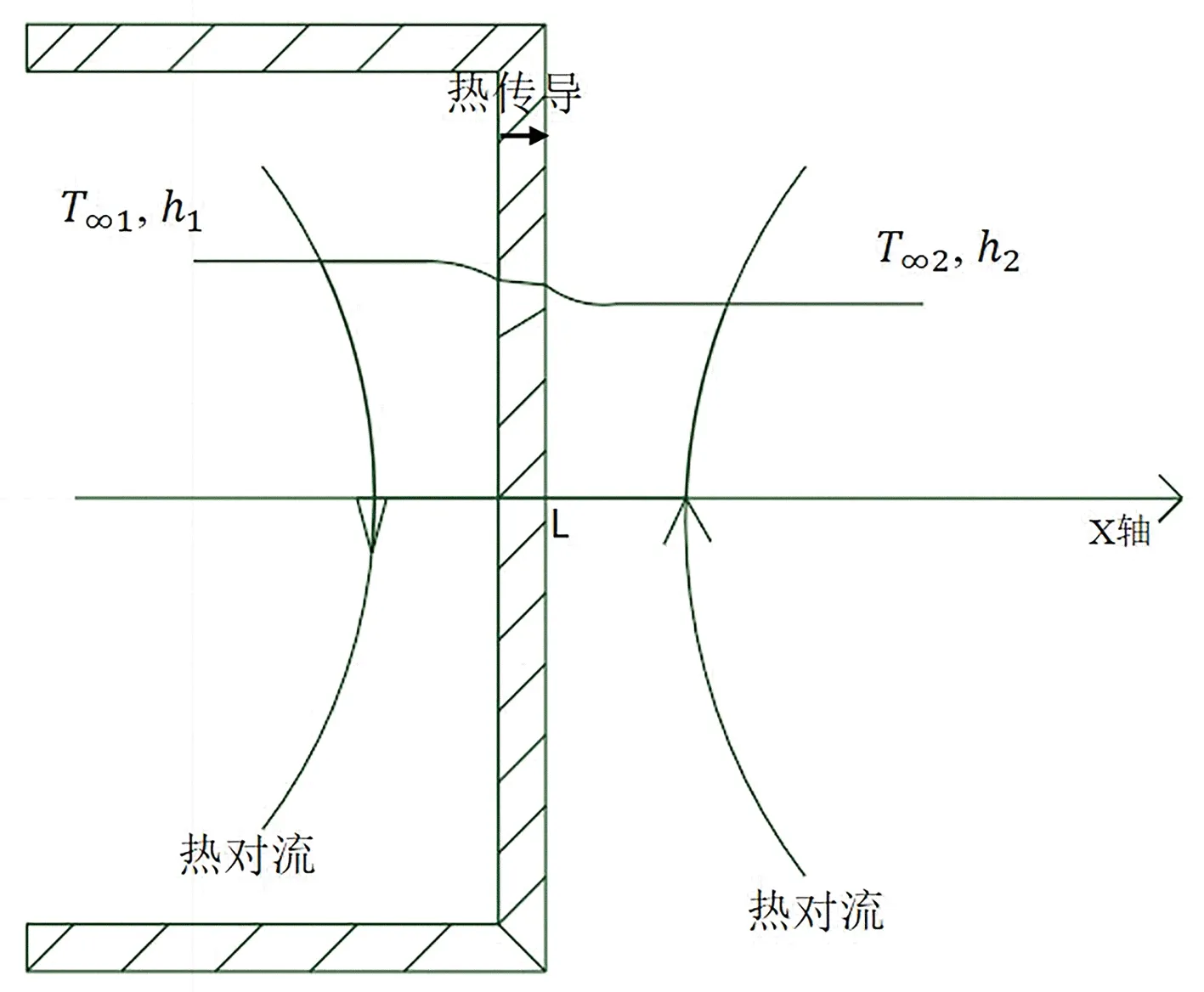
图4 玻璃展柜传热分析示意图

玻璃内部的热传导,满足傅里叶定律:

(6)

式中,q为热量通量密度;λ为玻璃的导热系数;x为温度变化方向的距离。

玻璃壁面与空气流体之间的对流换热的速率方程满足牛顿冷却定律:

q=h(TS-T∞)

(7)

式中,h为对流换热系数;TS为介质表面的温度;T∞为介质表面流体的温度。

如图4所示,选取x方向的一段玻璃壁面,玻璃厚度为L,玻璃的导热系数为λ;T∞1、h1、T∞2、h2分别为展柜内、外空气温度与对流换热系数。

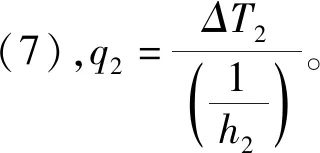
当展厅中央空调关闭,柜外空气温度上升,热量传递方向与上述过程相反,热量通过自然对流→热传导→自然对流的方式由柜外流入柜内。

此处的分析仅起说明用途,因此不考虑玻璃内热量积累,因此总的传热通量Q满足式(8),

Q=q1=q2=q3

(8)

结合上述q1、q2、q3的计算公式,得出总热通量的计算公式,如式(9)所示。

(9)

该式表明,展柜内外传热速率由内-外温差和总热阻决定,其中总热阻由内部热对流、玻璃内热传导以及外部热对流三部分热阻累加得到。

3.2 夏季工况模型标定

为考察模型的预测精度,并通过实验数据标定以提升模型的可靠性,本研究选取了一组典型的夏季工况下展柜外环境温度实测数据作为模型的边界条件,将柜内温度的预测值与实验监测值加以对比分析。通过调节模型参数(展柜玻璃导热系数λ)使得柜内温度的预测值更好地与实测值相吻合,以这种方式标定了模型,提升了模型的预测精度。

具体地说,模型以展厅中央空调制冷开启时间09∶00为模拟起始时间点,模拟了当日09∶00至24∶00间展柜内温度分布变化情况。模型的模拟结果如图5所示,红线代表初始模型对柜内温度的模拟结果,蓝色三角形代表柜内温度变化的实测结果,二者总体变化趋势一致。模拟结果与实测结果的平均偏差为0.29 ℃,最大偏差为0.57 ℃,两者间存在一定的误差。如果能利用实测数据对模型进行标定,可以进一步提升模型精度和可靠性。

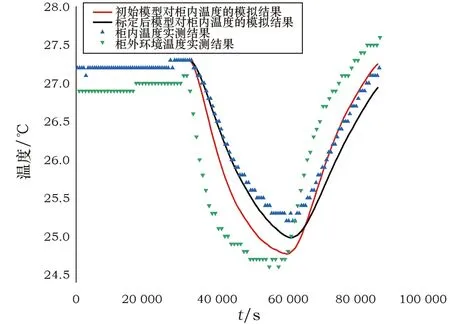
图5 夏季工况下展柜内温度变化实测结果与模拟结果的比较

由式(9)可知,柜内外热量传递过程与温差(ΔT)、对流换热系数(h1、h2)、玻璃厚度(L)、玻璃的导热系数(λ)有关。本研究中,将24 h内展柜外实测空气温度(T∞2)的瞬态变化数据作为计算域的边界条件给定,展柜与环境的自然对流换热系数(h2)根据文献值设定[16],展柜玻璃厚度(L)由实际测量得到,展柜内部空气的自然对流换热系数(h1)、展柜内空气的温度(T∞1)等均由数值分析的方式直接计算得出。以上参数均不能作为模型标定的可调节参数。在初始模型中,玻璃的导热系数根据文献按照普通玻璃的物性给定,但本展柜玻璃的隔热性更好(导热系数更小),造成了初始模型预测值与实验值的差异,因此本研究选取玻璃导热系数(λ)为模型标定的可调节参数,通过调节玻璃导热系数(λ)的数值,使模拟结果(图5中黑线所示结果)与实测结果(图5中蓝色三角形所示结果)总体误差最小,以达到模型标定的目的。

在初始模型中,玻璃导热系数(λ)的数值设定为0.77 W/(m·K)[16],此时模型预测的隔热效果不及实验测量结果,表明所设定的导热系数大于真实数值。为了实现对柜内实测温度曲线的最佳拟合,本研究采用夹逼算法[18],以玻璃导热系数(λ)为变量,在0.01～1 W/(m·K)区间内,以模型预测温度和实测数据的误差平方和为目标函数,求取目标函数达到区间极小值时的λ值,作为标定后的模型参数。此算法得到的玻璃导热系数λ值为0.029 W/(m·K),此时模拟结果与实测结果得到最佳吻合。从图5中可以看出,柜内温度实测值与模拟值之间的平均偏差为0.18 ℃,最大偏差为0.33 ℃,较初始模型均有所改善,说明标定后的模型的精度较初始模型有显著提升。上述结果证明,本研究中建立的CFD数值分析模型经标定能准确地预测夏季工况下展柜内部空气温度的实际变化情况。

3.3 冬季工况模型适用性分析

为进一步验证模型的准确性与适用性,考察标定后的模型是否能够准确模拟出不同工况下展柜内部的温度变化,本研究选取了一组典型的冬季工况下展柜外环境温度的实测数据作为上述模型的边界条件,在不进一步调整模型参数的情况下,直接进行模拟计算。

冬季工况下展柜内部温度变化的模拟结果与实测结果的对比如图6所示。从图中可以看出,模拟值和实测值间误差较小,二者之间平均偏差为0.029 ℃,最大偏差为0.081 ℃。以上计算结果说明,经夏季工况标定的模型能够很好地直接应用于冬季工况中。

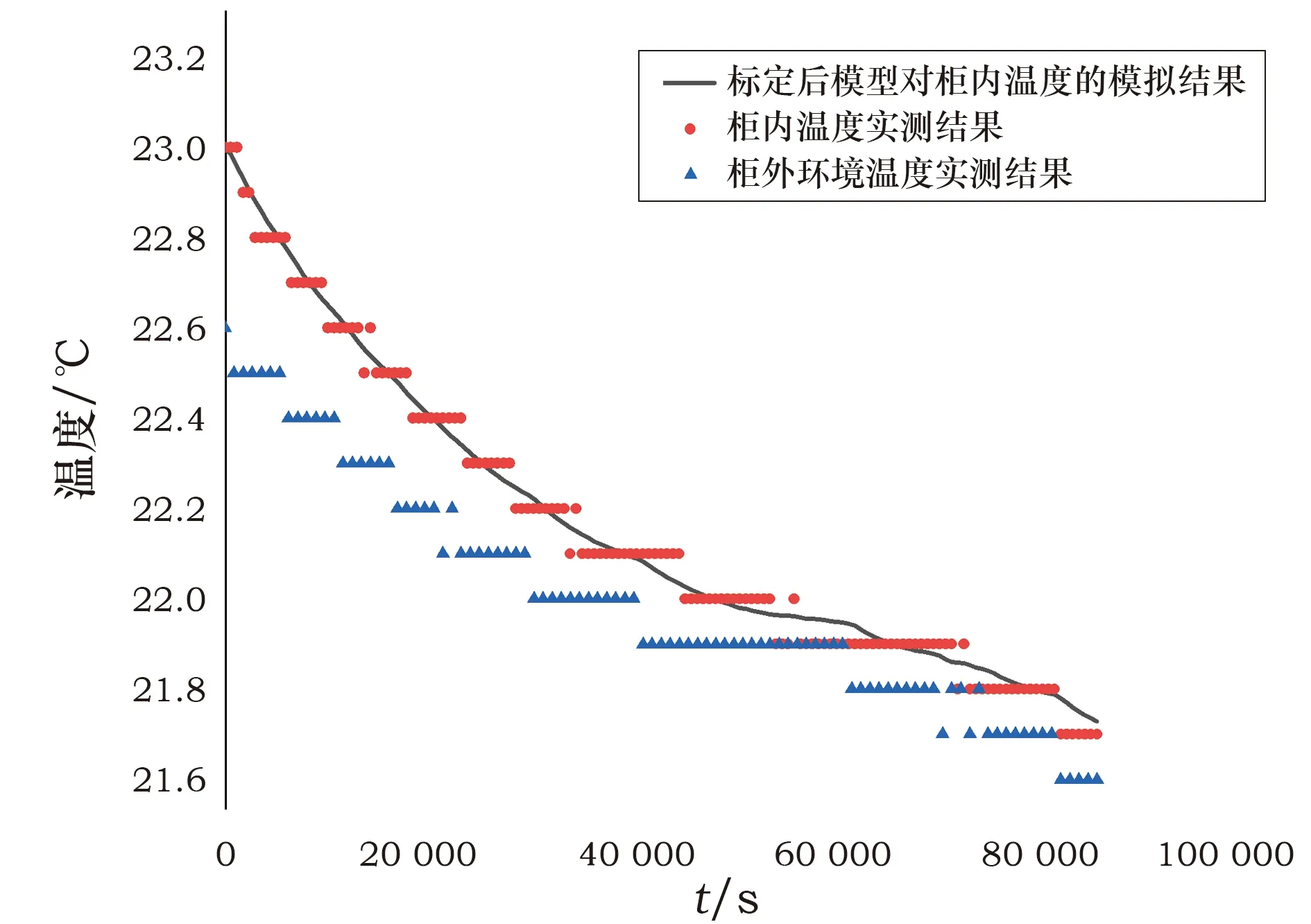
图6 冬季工况展柜内温度变化实测结果与模拟结果的比较

3.4 展柜内部温度场-流场分析

为实现环境温度瞬态变化条件下,展柜内温度、气流分布的可视化,本研究选取了模型在两季工况下不同时刻的模拟结果,对展柜内部温度场、空气流场的变化情况进行了描述。

夏季工况下,在模拟前期,展柜玻璃壁面温度低于柜内空气温度,如图7a、7b所示。展柜内部贴壁处的空气受展柜内壁面冷却,与内壁面间发生自然对流换热。此时,柜内空气流场分布如图7c所示,展柜中央存在上升气流,展柜内壁面附近存在下降气流,整体上形成了由中心向四周循环的自然对流。

图7 夏季工况下当日9∶30展柜内温度、气流的分布

展厅中央空调持续制冷,柜外空气温度持续下降,玻璃外壁面受对流换热的影响,温度随之下降;内壁面由于玻璃的热传导作用,温度也随之下降;在此过程中,展柜内部空气与内壁面也同时发生自然对流换热。17∶30左右展柜内温度分布如图8a、8b所示,此时,展柜底部由于与外界空气绝热,其附近温度略高于其他区域。此时,柜内气流分布如图8c所示,在一侧内壁面附近有垂直上升的气流,在另一侧存在下降气流,整体上形成了一个气流大循环。

当展厅中央空调关闭,柜外空气温度上升,至24∶00,温度分布如图9a、9b所示,此时,内壁面温度高于柜内空气温度,外界向柜内传热。柜内气流分布如图9c所示,展柜中央存在下降气流,展柜内壁面附近存在上升气流,整体上形成了由四周向中心循环的自然对流。

图8 夏季工况下当日下午5∶30展柜内温度、气流的分布

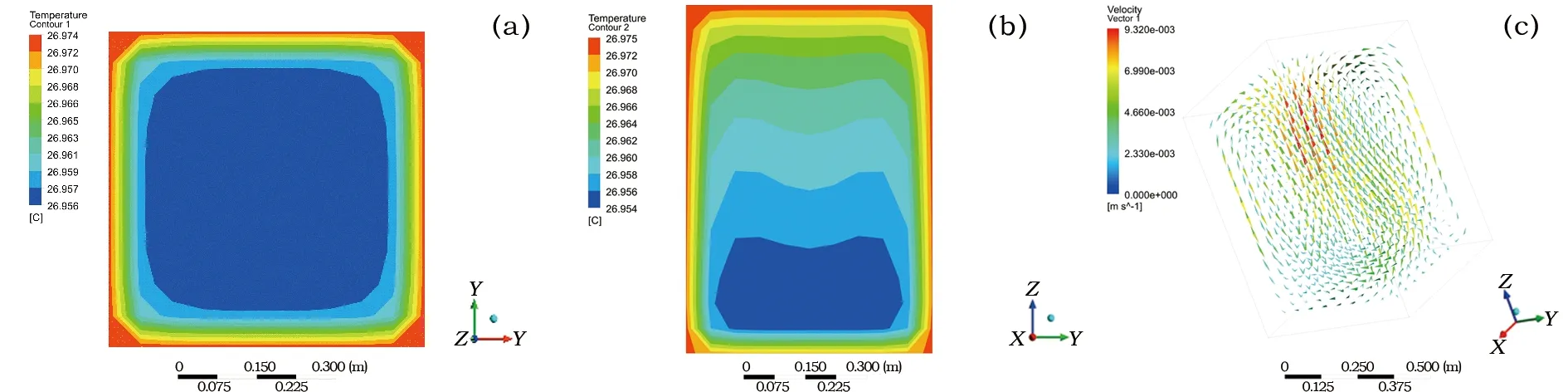
图9 夏季工况下当日24∶00展柜内温度、气流的分布

冬季工况下,展厅当日未开启中央空调制热,柜内空气温度随展厅温度的下降而下降,由图6所示,当日任意时刻柜内温度均高于柜外温度,柜内向外界传热。当日24时柜内气流分布如图10所示,展柜中央存在上升气流,壁面附近空气持续受内壁面冷却下沉,整体上形成了由中心向四周循环的自然对流。

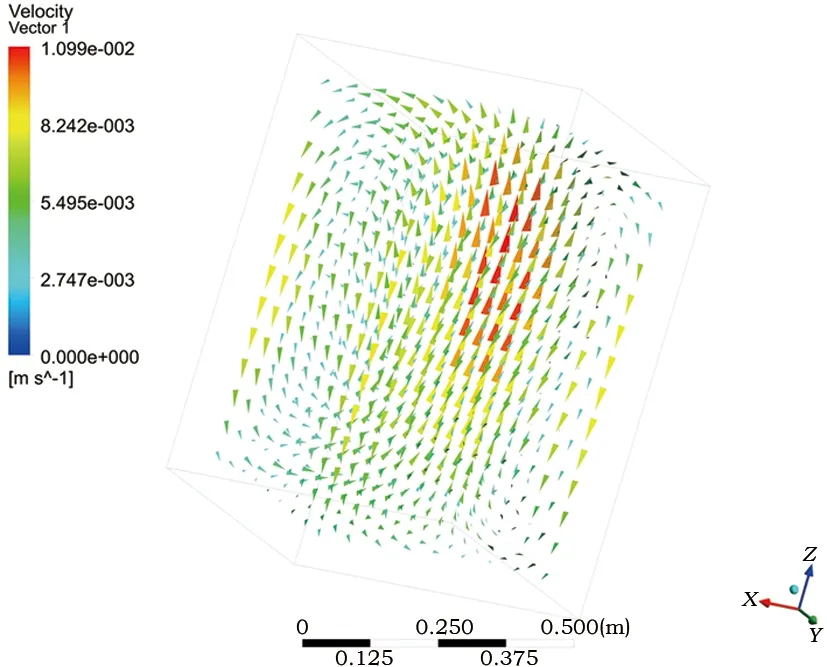
图10 冬季工况下当日24∶00展柜内部气流的分布

4 结 论

本研究使用计算流体力学(CFD)软件建立了能够反应展柜所处环境温度瞬态变化的三维CFD仿真模型,并成功地将展柜外实测温度数据使用UDF(User Defined Function)编译,作为模型的边界条件进行计算,得出以下结论。

1) 本研究利用了展柜外温度监测数据作为边界条件,建立了重庆中国三峡博物馆某独立展柜的瞬态CFD三维模型。该模型运行稳定。

2) 在夏季工况下,使用展柜内温度实测数据成功地对模型进行了标定。通过夹逼算法调整展柜玻璃的导热系数,使模拟结果与实测数据实现最佳拟合。二者拟合时,玻璃导热系数(λ)为0.029 W/(m·K),模拟值与实测值之间的平均偏差为0.18 ℃,最大偏差为0.33 ℃。

3) 在未调整模型参数的情况下,将上述模型直接应用在冬季工况中。模型仍表现出很好的预测效果,与柜内实测温度数据相比,二者平均偏差为0.029 ℃,最大偏差为0.081 ℃。该结果证明了标定后的模型在不同的工况中均有较好的预测效果,进一步验证了该模型的适用性与可靠性。

4) 模型成功地应用于描述展柜内部温度场、空气流场的变化,实现了柜内温度、气流分布的可视化,提升了我馆文物预防性保护手段的定量化与数字化水平。

上述结论证明,考虑瞬态环境温度变化的展柜三维CFD分析模型能够有效利用现有监测数据,以快速、低成本的方式对文物保存微环境温度进行较准确地预测,从而定量地评估并优化文物保存微环境的监控措施。另一方面,展柜的瞬态三维CFD模型实现了展柜内部温度、气流分布的可视化。研究证明CFD仿真建模技术在文物预防性保护领域具有广阔的应用前景。