基于偏微分方程约束的机器人群集运动控制系统设计

董 慧

(西安明德理工学院 通识教育学院，西安 710124)

0 引言

机器人可以从许多不同的角度协助或取代人类，完成危险的工作。在人工智能理论以及控制理论不断发展和成熟的大背景下，机器人的工作范围和复杂性也越来越高，但人们对机器人提出了更多新的要求，而单个机器人能力难以满足这些新的应用需求[1]。为此提出了多个独立机器人相互协调合作的工作模式，即形成机器人群集，使其共同完成给定的任务。相对于单一机器人，机器人群集可以实现一些单一机器人无法完成的工作，因此在完成任务时可能具有更高的效率。

鉴于机器人群集在工作性能方面的优势，目前机器人群集已经应用到军事、工业生产、交通控制等领域，且具有良好的应用前景。然而机器人群集在实际的应用与运行过程中，群集中的机器人会相互碰撞，影响机器人集群的运动效果以及工作效率。为了保证机器人集群的高效运动，设计并开发了机器人群集运动控制系统。机器人群集运动控制是指在控制指令的驱动下，通过执行元件或电机的运行调整单一机器人的运动参数，使机器人群集能够按照既定方案执行运动任务。

从现阶段机器人群集运动控制系统的设计与应用情况来看，当前相关领域学者已经研究出了较为成熟的控制系统。文献[2]提出基于输出反馈线性化的运动控制系统主要应用于单一机器人的运动控制工作中，将其应用到机器人群集的控制工作中，存在部分机器人无法控制的情况，最终影响系统的控制效果。文献[3]提出基于领航跟随的运动控制系统主要是控制机器人群集中的主机器人，在此基础上采用跟随模式控制从机器人，保证从机器人与主机器人的运动参数与路径一致，因此该系统只能应用于重复操作的运动任务中，在应用范围上存在一定的局限性。为了解决上述运动控制系统存在的问题，引入偏微分方程约束理论。

偏微分方程是指未知函数的偏导数或者偏微分的方程。在客观环境下，偏微分方程可以表达为时间坐标和变化规律，往往表现为关于时标的各阶变化率之间的关系式。偏微分方程约束理论的工作内容就是根据时标的各阶变化率之间的关系设置约束条件。本文首先通过改装机器人传感器、运动控制器和驱动电机设备，优化了机器人群集运动控制系统硬件设备。在此基础上将偏微分方程约束理论应用到机器人群集运动控制系统的优化设计工作中，将规划路径作为机器人群集运动的约束条件，以位置和姿态角来计算运动控制量，根据计算结果生成控制指令，实现机器人群集运动控制系统设计。

1 机器人群集运动控制系统硬件设计

机器人群集运动控制系统硬件主要包括通信网络、传感器、运动控制器、驱动电机，硬件整体的组成如图1所示。

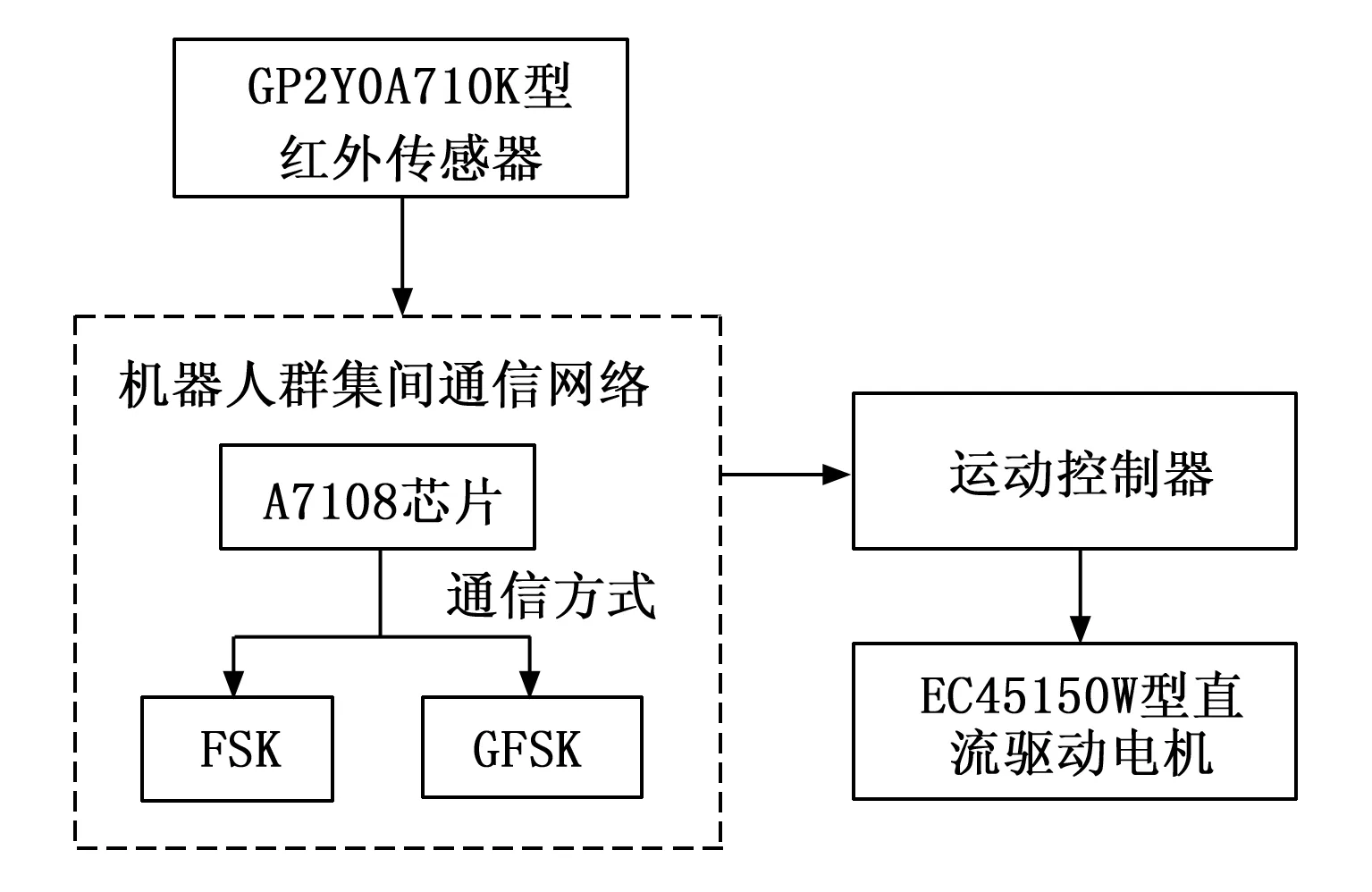
图1 硬件整体组成框图

如图1所示，机器人群集运动控制系统的硬件由通信网络相连，通过GP2Y0A710K型号红外传感器获取机器人的位置信息和运行参数信息，通过通信网络将信息传输至运动控制器，由运动控制器实现计算机器人的位置信息的任务，再将控制信息传输至运动驱动电机，生成不同方向的驱动信号。

1.1 机器人群集间通信网络

通信在多机器人系统的研究中有着重要的作用，借助通信可以获取任务需求、环境信息和邻居状态等，为了提高机器人群集的运动控制效果，通过局部通信来扩大感知范围。在传统通信网络的基础上，将射频芯片替换成A7108，以该芯片为核心部件的通信网络的数据传输速度支持2～250 kbps，支持FSK和GFSK两种通信方式，在10 kbps的工作条件下，其通讯距离能够达到1 600 m。A7108芯片除具备远程传送功能外，还具有检测通道及晶片内部机制的功能，可有效克服半导体制程的变异特性，使其能够在各种恶劣环境下工作，有效地解决因射频频偏而引起的灵敏度下降问题。

1.2 机器人传感器

在各个机器人上安装传感器的目的是获取机器人的位置信息和运行参数信息，从而确定当前机器人的初始状态。控制系统中装设的位置传感器为红外传感器，型号为GP2Y0A710K，该设备不仅能够确定机器人在环境空间中的实时位置，也能够利用红外信号来分辨方向。系统中的红外传感器由发射头和接收头构成，其中接收头内包括内置的增益控制电路、解码电路和带通滤波器。系统中红外传感器的工作电路如图2所示。

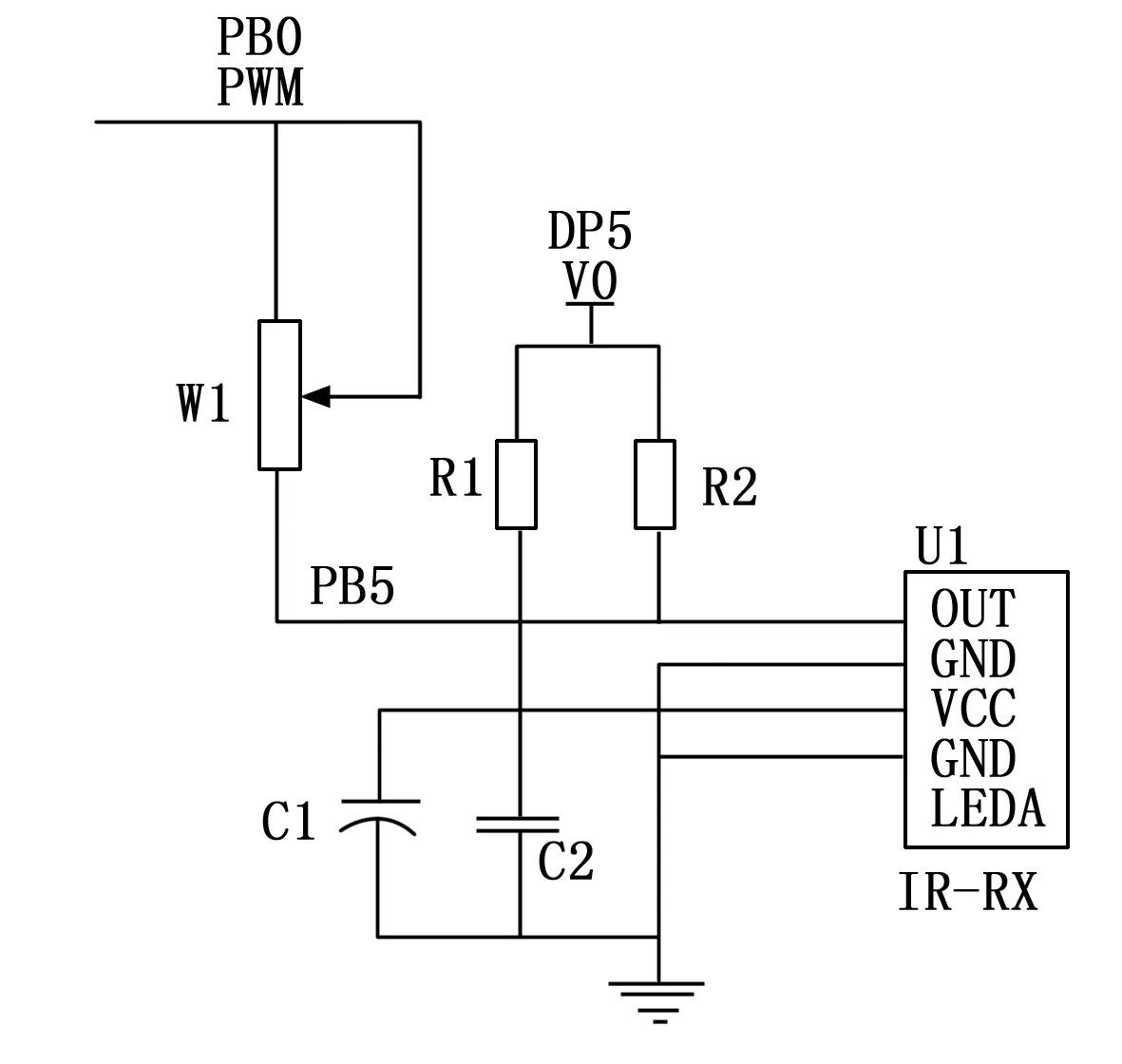
图2 系统红外传感器工作电路图

在运行过程中，发射端可以发出红外线的频率，当红外线碰到障碍时，会被反射回去，而红外线会被红外线接收，而处理器则会根据红外线接收器的电压变化，判断出机器人和障碍物的距离。

1.3 机器人群集运动控制器

机器人群集运动控制系统以控制器作为执行元件，用来生成运动控制任务，同时完成协同通信、实时解算控制数据等功能。另外要求安装的运动控制器需要有精确、稳定地控制时间频率，以保证跟随运动精度[4]。为满足上述要求，在传统运动控制器的基础上进行改装，改装的运动控制器内部结构如图3所示。

图3 机器人群集运动控制器内部结构图

从图3中可以看出，机器人集群运动采用位置、速度、电流驱动并行控制方式，位置控制采用PID控制，而速度和电流驱动采用PI控制[5]。此外，在运动控制器中嵌入复位器、低电压检测等的集成电路，用以支持实时解算控制数据等功能的运行。

1.4 机器人运动驱动电机

在移动机器人的运动中，通过传感器的反馈，可以随时调节电机的转速。在接收到传感器的反馈信息之后，主控芯片会根据输出电压和输出电压的误差，计算出输出电压[6]。机器人的运动驱动装置是EC45150W型直流驱动电机，其输入端可以与主控芯片相连，这样就可以很方便地进行控制。图4为机器人运动驱动电机的驱动电路。

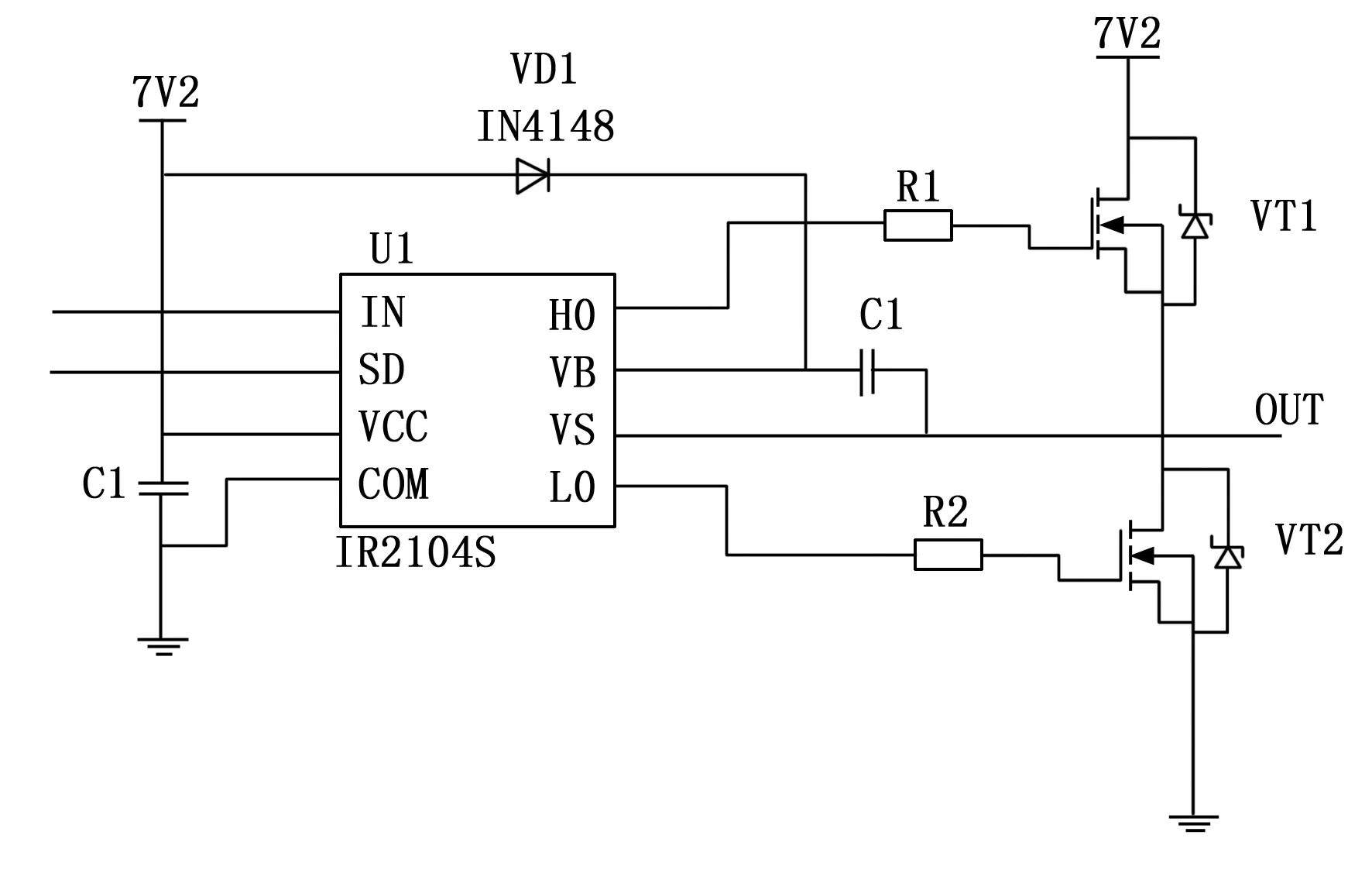
图4 机器人运动驱动电路图

启动驱动电机后，通过改变输入端IO口的逻辑电平，即可实现电机正转和反转的切换，从而生成不同方向的驱动信号。最终利用通信网络连接驱动电机、传感器与控制器，并将其接入到供电电源中。

2 机器人群集运动控制系统软件功能设计

在硬件设备的支持下，通过确定机器人群集运动控制逻辑以及控制程序编写等步骤，完成系统的软件设计[7]。优化设计系统采用集中式控制方式，即具有完整信息和绝对控制权的中央处理器。集中式控制方式是由上至下的分层体系，由规划和决策组成。在具体的实施中，中心处理器对各个独立的个体进行数据的分析，制定出一个整体的计划方案，然后再向机器人群集中的各个机器人发出指令。

2.1 建立机器人群集数学模型

机器人群集由多个单一机器人组成，机器人群集可以量化表示为：

U={ui∣1≤i≤nrobot}

(1)

其中：nrobot为机器人群集中单一机器人的数量，组成群集的机器人可能是同构的，也可能是异构的。机器人之间保持通信交互，在任一时刻任意两个机器人之间的位姿关系可以表示为：

(2)

式中，xi、yi和θi代表机器人i的当前位置和姿态角，dij为两机器人之间的间隔距离，φ表示的是机器人j的偏转角[8]。为了保证系统能够对机器人群集中的所有机器人设备进行精准控制，需要在执行控制任务前对群集中的各个机器人进行匹配。依据 Euler-Lagrangian 原理，将单一机器人的动力学模型建立为：

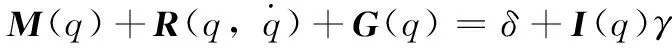
(3)

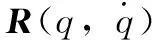
2.2 分配机器人群集运动任务

假设机器人群集待执行的运动任务集合为W，其量化表达式如下：

W={wk∣1≤k≤ntask}

(4)

其中：ntask为运动任务数量。根据运动任务的优先与重要程度，对每个运动任务进行加权，任意运动任务的权值标记为ϖi。那么机器人群集的运动任务分配问题可以描述为：

(5)

式中，变量gik为需要求解的任务分配结果，ψik为机器人对于运动任务的效用值[9]。

2.3 利用偏微分方程规划机器人群集编队运动路径

机器人群集编队运动路径的规划大体可以分为4个步骤，分别为机器人定位、障碍物检测、机器人群集编队以及运动路径生成与平滑处理，在路径轨迹生成阶段利用偏微分方程来反映机器人的实际环境信息，从而得出更符合实际环境的路径规划结果[10]。假设函数h在区域Z内具有方程中出现的各阶连续偏导数，把h代入到Z区，若h能够将Z区转换为恒等式，则h为Z区方程的解。在n+1维中，h为方程的积分曲面。将机器人群集的运动规律用偏微分方程来表示，其数学表达式如下：

(6)

式中，t为机器人群集的运动时间，β为偏微分系数。在实际的路径规划过程中可用从起点到终点波动的二维方程描述[11]。利用硬件系统中的传感器设备，确定机器人的当前位置信息，机器人初始位置的定位结果可以表示为：

(7)

其中：(xKnown，yKnown)为运动环境中的已知节点位置坐标，υinfra-red为传感器产生红外信号在环境中的传输速度，Δt代表信号的传送时间，ϑ为机器人位置与已知节点位置之间的夹角[12]。在此基础上，根据机器人群集运动任务的分配结果，确定机器人群集的编队方案。根据机器人群集的编队结果，确定编队运动路径的终点位置，机器人当前位置与编队运动终点位置之间的连线即为机器人集群运动的初始路径[13]。利用式(8)计算机器人群集初始编队运动路径与运动环境中障碍物的重合度。

(8)

式中，i表示的是初始运动路径上的任意一点，(xobstacle，yobstacle)为机器人运动环境中障碍物的位置坐标。若运动环境中存在的障碍物数量不为1，则需要对重合度进行一一匹配[14]。若初始路径中的节点与障碍物之间的重合度趋近于1，则认为障碍物处于规划的初始路径上，需要对路径上重合节点的位置进行调整，调整结果如下：

(9)

式中，εx0和εy0为位置调整系数。按照上述方式对初始路径上的所有节点进行检测与调整，根据路径节点与初始节点之间的距离，依次连接路径节点，完成路径的更新工作[15]。最终对更新的运动路径进行插补处理，得出机器人的运动步长和步数为：

(10)

其中：υGive和Tinterpolation分别为机器人的给进速度和插补周期，Ps和Pe为更新路径的起点和终点。NSteps取整后确定步长的具体取值。按照上述方式对机器人群集中的所有机器人的路径规划结果。

2.4 设置机器人群集运动约束条件

在偏微分方程约束理论支持下，将机器人群集的实时位置作为机器人群集运动约束条件，保证机器人位置始终处于区间[Pi-0.5，Pi+0.5]内。通过积分、微分运算，把它转化为有约束的对象在真实的空间中的位置[16]。根据全约束体系的特点，可以将其转换成具有较高阶的非约束体系，从而使整个约束体系的研究和应用更为精确和完善。另外设置机器人群集运动控制的完整性约束条件为：

φ(ζ，t)≥0

(11)

其中：ζ为机器人在空间运行时自身的姿态，φ(ζ，t)为t时刻机器人运动状态函数[17]。最终融合位置和姿态约束条件，并输入到各个机器人设备上。

2.5 计算机器人群集运动控制量

在机器人群集的运动过程中，利用传感器设备实时检测机器人的位置和姿态角数据，并与规划的运动路径进行比对，得出任意机器人运动控制量的计算结果。运动控制量的计算过程可以表示为：

(12)

式中，(xi(t)，yi(t))和(xi，P(t)，yi，P(t))分别代表t时刻机器人i的实际位置和规划位置，θi(t)和θi，set(t)表示机器人i姿态角的实际值和目标值。由此完成机器人群集运动控制量的计算工作。

2.6 实现机器人群集运动控制

在规划运动路径和设置条件的约束下，将计算得出的机器人群集运动控制量输入到控制器中，控制器自动生成的控制指令可以表示为：

(13)

式中，κ1和κ2均表示控制参数，其具体取值由控制器的工作方式决定，变量d为规划运动路径的长度，ϑcontrol表示参考框架水平轴和连接机器人运动中心与目标位置向量之间的夹角，ϑf为机器人目标位置在全局环境中的方位角[18]。根据生成的机器人群集运动控制指令，利用公式(14)计算出机器人左右驱动轮的电机转速。

(14)

式中，参数Lwheel为左右驱动轮的中心距离，将式(13)的计算结果代入到式(14)中，即可得出左右驱动轮电机转速υleft和υright的计算结果，并将其直接作用在机器人的驱动电机上。按照上述方式，生成机器人群集中所有单一机器人的实时控制指令，从而完成对机器人群集的运动控制[19]。在实际控制过程中，需要实时更新机器人群集的运动数据以及环境数据，若检测发现当前机器人位置出现偏差需重新生成控制指令，若检测发现环境中出现新的障碍物，且障碍物与规划路径重合，则需要利用偏微分方程生成新的运动路径。

综上可得出机器人群集运动控制系统软件流程如图5所示。

图5 机器人群集运动控制系统软件流程图

3 系统测试

以测试基于偏微分方程约束的机器人群集运动控制系统的控制效果为目的，选择Webots作为系统的开发运行平台，设计系统测试实验。Webots平台能够快速还原环境场景，允许用户通过物理性质建立机器人模型，从而实现控制指令的生成与传输。Webots平台提供了一个传感器库，便于在机器人样机中插入传感器并对传感器的工作参数进行调整[20]。除此之外，Webots平台还支持偏微分方程的运行程序，从而保证基于偏微分方程约束在机器人群集运动控制系统中的正常运行。为体现出优化设计系统在运动控制效果方面的优势，设置传统的基于输出反馈线性化的运动控制系统和基于领航跟随的运动控制系统作为实验的对比系统。

3.1 准备机器人群集样机

此次系统测试实验选择的机器人型号为LS20，属于微型移动机器人，其硬件和软件均完全开放。LS20机器人以双轮作为移动元件、差分电机作为驱动装置，机器人直径约为8.2 cm，重量约为180 g，机器人主要由塑胶零件构成，内置动力电池，并可拆卸，因此不会因充电而发生停机。此次实验共准备5台相同型号的机器人，组成机器人群集。

3.2 配置机器人群集运动环境与初始位姿

为验证优化设计机器人群集运动控制系统的有效性，布置无障碍和有障碍两种室内实验环境，其中无障碍环境保证机器人群集的运动路线上无障碍，而有障碍环境是在无障碍环境的基础上，加设多个纸盒箱作为障碍物，障碍物的设置位置随机。在配置的实验环境中，布设机器人群集，具体的布设情况如图6所示。

图6 机器人群集初始位姿与运动环境示意图

从图6中可以看出机器人群集在初始状态下呈一字横队分布，并将所有机器人的初始工作参数设置成默认值。

3.3 生成机器人群集运动目标路径

按照一字横队的编队方案，结合实验运动环境的布设情况，生成机器人群集运动目标路径，一字横队方案下机器人路径的规划结果如图7所示。

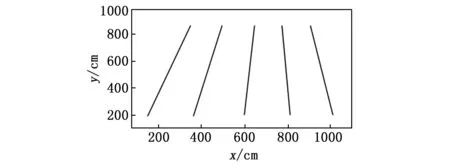
图7 机器人群集运动目标路径规划结果

根据机器人群集运动目标路径的规划结果，生成系统的运动控制任务，并记录任意时刻各个机器人的位置坐标和姿态角，以此作为系统运动控制任务的目标值。

3.4 设置系统测试指标

此次系统测试实验分为两个部分，分别为机器人群集运动路径的跟踪控制和机器人群集的避障控制，其中机器人群集运动路径跟踪控制效果的测试指标为位置控制误差，其数值结果如下：

(15)

式中，xi、yi、xP，i和yP，i与式(12)一致，nrobot为群集中包含的单一机器人数量，系统测试实验中取值为5。计算得出位置误差值越大，证明对应系统的运动路径跟踪控制效果越差。另外机器人群集避障控制的量化测试指标为碰撞次数，其测试结果为：

Ncollision=Nr-r+Nr-o

(16)

其中：Nr-r和Nr-o分别表示机器人之间以及机器人与障碍物之间的碰撞次数。系统控制作用下，机器人碰撞次数越多，证明对应系统的避障控制效果越差。

3.5 系统测试过程与结果分析

将优化设计控制系统的硬件设备安装在机器人设备上，将所有硬件设备调整至运行状态，将其接入到通信网络环境中。将实验系统以及对比系统编写成程序代码，导入到主测计算机中，实现系统的开发。

3.5.1 运动跟踪控制实验

在无障碍物环境下，导入生成的机器人群集运动轨迹，执行运动控制程序，完成运动跟踪控制任务。系统执行运动跟踪控制时的运行界面如图8所示。

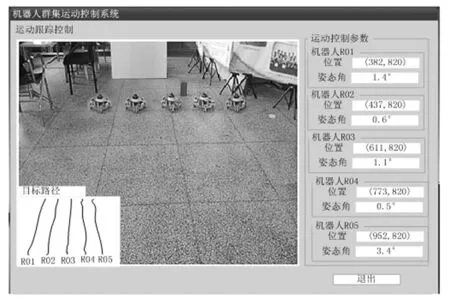
图8 机器人群集运动控制系统运行界面

在完成一次机器人群集运动控制任务后，重置机器人运动数据，将控制系统切换至对比系统，执行相应的控制程序。统计各个机器人的实时运动数据，得出反映系统运动跟踪控制效果的测试结果，如表1所示。

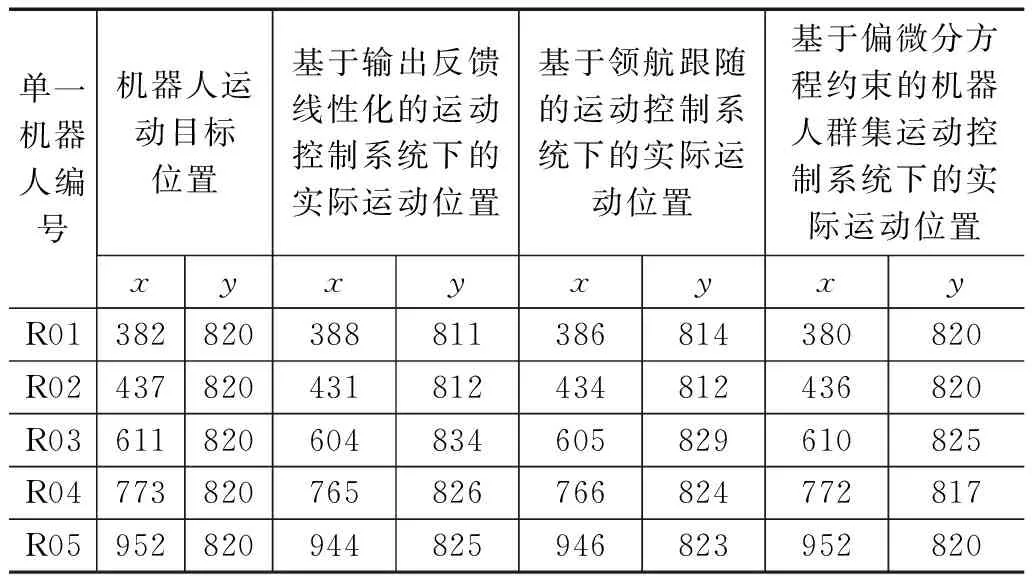
表1 系统运动跟踪控制效果测试数据表

将表1中的数据代入到式(15)中，计算得出传统控制系统下机器人群集的运动跟踪控制误差分别为77 cm和56 cm，优化设计基于偏微分方程约束的机器人群集运动控制系统下的运动跟踪控制误差为13 cm。由此证明优化设计的运动控制系统具有更好的运动跟踪控制效果。

3.5.2 机器人群集避障控制实验

在有障碍物环境下，重复执行运动与控制工作，记录各个机器人的碰撞信息，经过式(16)的计算得出碰撞次数的测试结果，如图9所示。

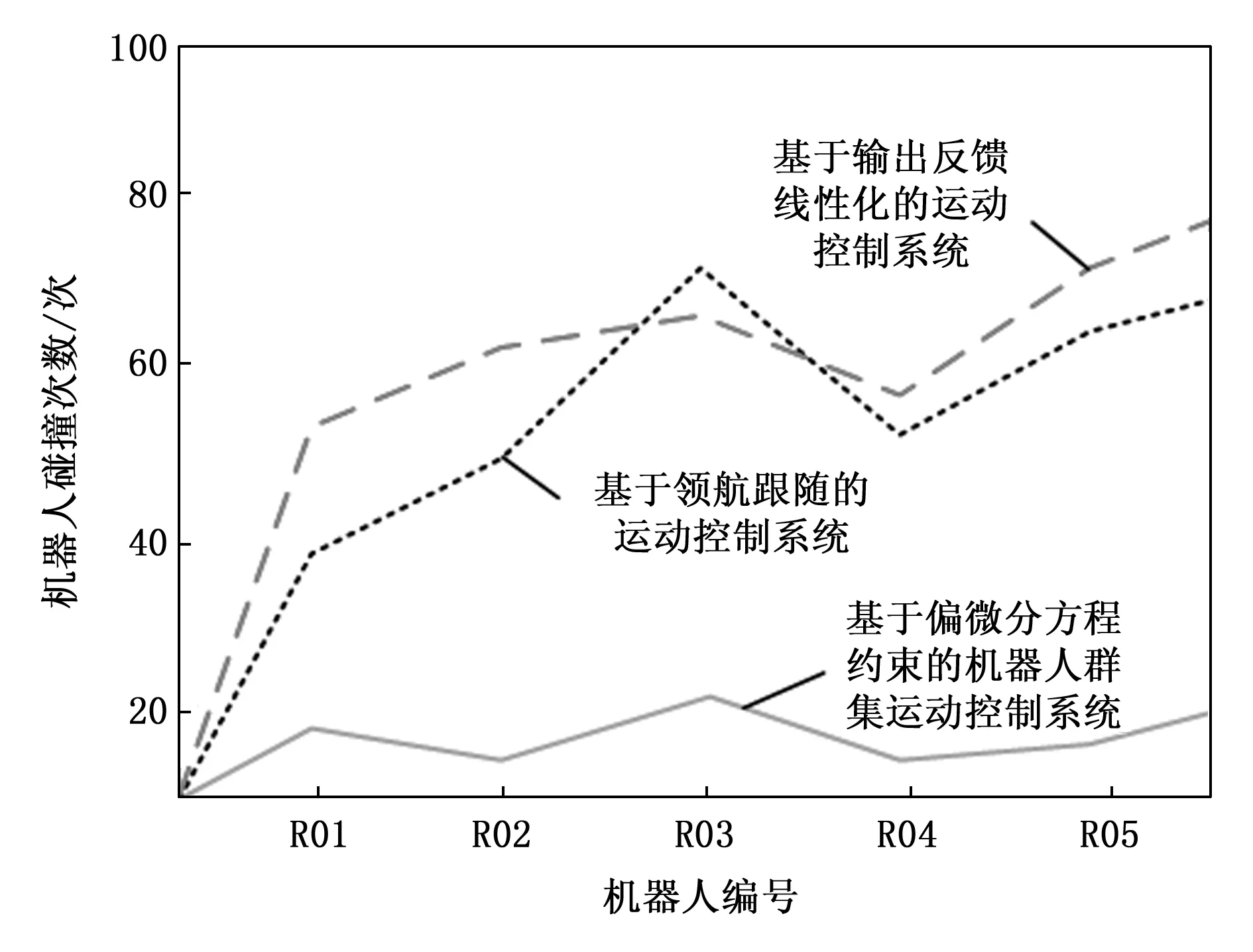
图9 机器人群集避障控制实验结果

从图9中可以直观地看出，与传统运动控制系统相比，在优化设计的机器人群集运动控制系统下机器人的碰撞次数明显降低，其中，基于输出反馈线性化的运动控制系统的平均碰撞次数为60次，基于领航跟随的运动控制系统的平均碰撞次数为53次，基于偏微分方程约束的机器人群集运动控制系统的平均碰撞次数为15次，即优化设计系统的避障控制效果更佳。

4 结束语

机器人群集是机器人工作的最新方式，能够解决单一机器人在大型工作中的局限性。在此次研究中，通过偏微分方程约束理论的支持下，生成机器人群集运动控制的精准约束条件，提高机器人群集在面对同时作业任务时的问题解决能力，从而帮助人们摆脱繁重、重复性高的劳动。从系统测试结果中可以看出，优化设计的机器人群集运动控制系统在运动跟踪和避障方面具有良好的控制效果，运动跟踪控制误差为13 cm，群集运动过程中碰撞次数平均值为15次，对于提高机器人群集的工作效率以及延长机器人的使用寿命具有积极意义。然而受到空间和时间的限制，此次系统测试实验忽略了对机器人姿态角的测试，且设置的测试数量任务数量较少，测试结果存在一定的偶然性，为此在今后的研究工作中还需要对测试数据进行补充。