环北部湾广东水资源配置工程深埋隧洞段初始地应力场反演分析
2023-04-25代志坤游思琴
代志坤,郑 晓,游思琴
(中水珠江规划勘测设计有限公司,广东 广州 510630)
地应力是天然状态下岩体中赋存的应力,是地球发展运动的结果,它是地球历次构造运动产生的。岩浆活动、风化剥蚀、地壳运动等都是地应力形成的重要因素,地应力是以上多种因素的多次综合作用之后的结果。目前还不可能做到根据地应力形成的过程来求解可供工程使用的初始地应力场[1-2]。但是初始地应力是地下洞室设计的主要荷载之一,正确选取地应力的量值和方向是设计工作的关键,且地应力也是工程计算的重要初始条件之一,工程实践中,初始地应力场的确定是岩石力学的一个重要研究内容,准确的查明初始地应力分布规律对地下工程的建设有重大意义[3-4]。获得工程区地应力数据的最直接有效的方式是进行地应力测试,进行大量的地应力测试需要大量的时间及预算,且测量成果受测量误差影响会有一定的离散性,只能反应局部地应力情况[5],尤其是在工程范围较大时,例如大型引调水工程、交通工程及铁路工程等,线路动辄几十、上百千米,地形地貌及地质构造差异较大,通过大规模的地应力测试来确定工程区内的初始地应力场,所耗费的时间和资金是难以承受的,在工程勘察期往往仅能在局部进行有限的地应力测试[6]。随着计算机技术发展,利用数值模拟技术,并结合有限的实测数据,对工程区地应力进行反演分析,是一种获得初始地应力场分布规律的有效方法[7-14]。
目前,常用的地应力反演方法有边界荷载调整法、应力(位移) 函数法、多元线性回归分析法、偏最小二乘法、位移反分析法、快速应力边界法(S-B法)、神经网络、灰色理论、遗传算法、变差函数法、模糊理论等方法[15-21]。
鉴于多元线性回归分析法具有方便快捷、易于掌握、惟一解的优势[9],本文采用多元线性回归分析法,计算结果表明,使用该方法能够得到合理的初始地应力场数据。
本文利用有限差分软件FLAC3D对环北部湾水资源配置工程输水隧洞埋深最大的洞段建立三维地质模型并进行地应力反演计算,结合勘察期地应力测试成果,同时利用多元线性回归分析法对工程区地应力进行回归分析,并建立初始地应力归回方程,最后根据回归分析结果利用FLAC3D重构工程区初始地应力,比对各监测点的反演值及实测值后可知,采用该方法可以有效的反演分析工程区的初始地应力分布,为该工程的深埋隧洞支护设计及施工开挖提供有效的理论及数据支撑,对工程建设实施有重要的指导意义。
1 反演分析的方法及原理
1.1 地应力反演分析思路
基于地形地质资料,结合对工程区地应力场条件的认识,建立三维模型,分析并确定主要的地应力影响因素及边界条件,然后进行数值模拟分析,选择相应的分析方法,建立地应力实测值及模拟观测值之间的联系,进而确定工程区初始地应力场的分布规律,具体流程见图1。
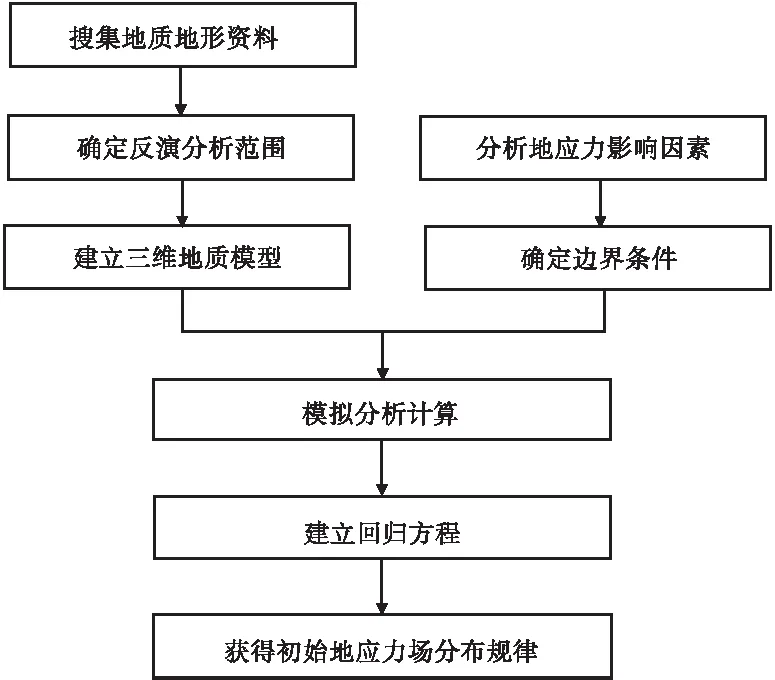
图1 地应力反演思路流程
1.2 模拟分析因素及边界条件
本文选择6种因素作为模拟岩体自重和地质构造力作用的基本因素[1]:①自重应力;②X向均匀挤压构造运动;③Y向均匀挤压构造运动;④水平面内的剪切构造(XY面);⑤垂直平面内的剪切变形构造(XZ面);⑥垂直平面内的剪切变形构造(YZ面)。
对于边界条件,有添加初始应力和初始位移两种方法,本文采取设置初始位移法来模拟地质构造运动。FLAC3D软件无法添加初始位移,可以通过施加节点速度分量的方式来设置位移边界条件。根据计算收敛情况设置在各种工况下的节点速率及计算步数。
工况1:仅考虑自重作用,见图2a。
工况2:仅考虑x轴向挤压构造运动,见图2b,计算时以边界位移为控制对象,控制单位取为1 cm,设置节点速率xvel= 2×10-6m/步,计算步数为5 000步。
工况3:仅考虑y轴向挤压构造运动,见图2c,计算时以边界位移为控制对象,控制单位取为1 cm,设置节点速率yvel=2×10-6m/步,计算步数为5 000步。
工况4:仅考虑xy平面剪切构造运动,见图2d,根据文献[22],长边和短边剪切位移应呈相应比例,长边位移取3.6 mm,短边位移取6 mm;边界节点速率分别为yvel=7.2×10-7m/步、xvel=1.2×10-6m/步,计算步数为5 000步。
工况5:仅考虑xz平面剪切构造运动,见图2e,地形面自由,边界剪切位移取9 mm,边界节点速率zvel=1.6×10-6m/步,计算步数为5 000步。
工况6:仅考虑yz平面剪切构造运动,见图2f,地形面自由,边界剪切位移取9 mm,边界节点速率zvel=1.6×10-6m/步,计算步数为5 000步。
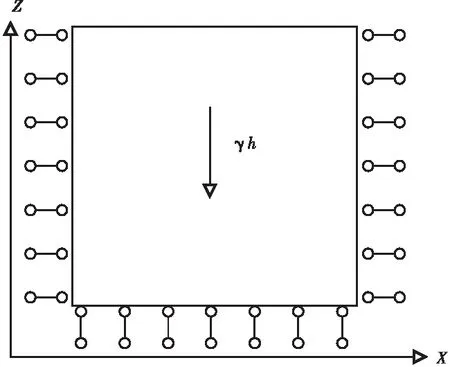
a)自重作用
1.3 多元线性回归分析原理[9]
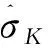
(1)

假设有m个观测点,则最小二乘法的残差平方和为式(2):
(2)

解此法方程式,得n个待定回归系数L=(L1,L2,L3,…,Ln)T,则计算域内任一点P的回归初始应力,可由该点边界荷载工况有限元计算值迭加而得式(3):
(3)
2 工程区地应力反演分析
2.1 工程概况
环北部湾广东水资源配置工程位于广东省西南部,该工程区主体所属一级大地构造单元为华南褶皱系,二级大地构造单元为粤西隆起区(Ⅱ1)、雷琼坳陷(Ⅱ6)、粤北、粤东北-粤中坳陷带(Ⅱ5),其中主干线位于粤西隆起区,分为3个三级大地构造单元:大瑶山隆起(Ⅲ1)、罗定坳陷(Ⅲ2)、云开大山隆起区(Ⅲ3)。该工程自西江干流取水,采用隧洞、暗涵、倒虹吸、渡槽等多种建筑物形式,穿越云雾山山脉、罗定盆地及云开大山,输水干线长约200 km,其中输水隧洞总长占比约80%。该工程干线输水隧洞属于超长深埋大洞径水工隧洞,隧洞单段最长约60 km,埋深一般均超过200 m,最大埋深910 m,开挖洞径将近10 m。
2.2 计算范围及计算模型
本文选取输水隧洞埋深最大的区域进行研究。根据工程区地质条件、水文条件及实测点的分布情况,为了消除人工边界误差在重要结构部位的影响,计算范围确定如下:以实测点为中心区域,垂直隧道走向为X轴,平行于隧洞走向为Y轴,竖直向上为Z轴;X轴及Y轴的计算范围为600 m×1 000 m,Z轴方向从高程-90 m至自然地面。计算区域X轴及Y轴方向分别为S60°E、N30°E。计算区域范围及测点平面位置见图3。共划分六面体单元120 000个,节点128 061个,计算网格划分情况见图4。假设工程区岩体为连续弹性体,采用线弹性本构模型模拟岩体力学行为。FLAC3D线弹性本构模型涉及的力学参数包括弹性模量、泊松比及密度(表1)。
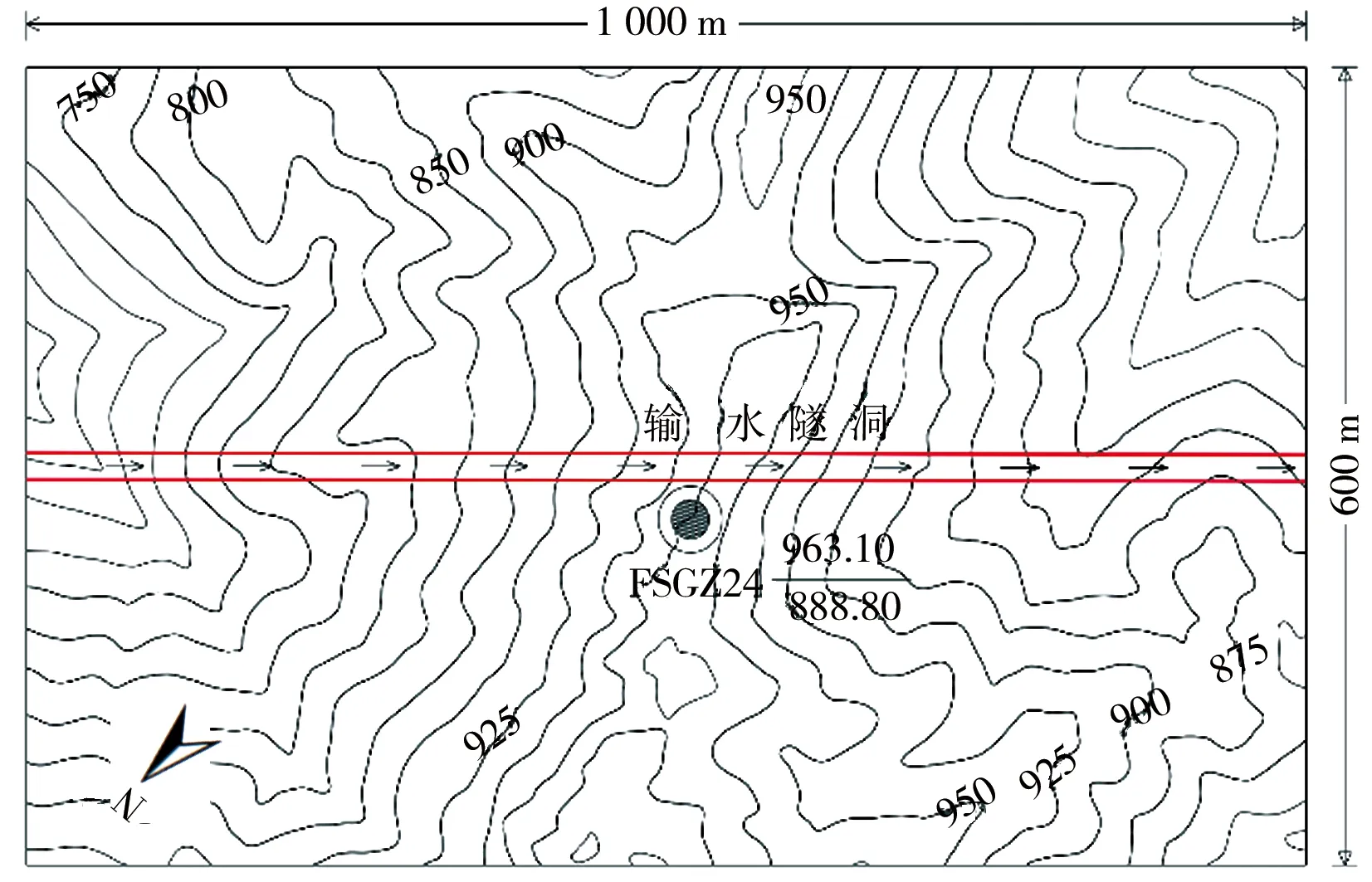
图3 计算区域及测点平面布置

表1 工程区区岩体力学参数
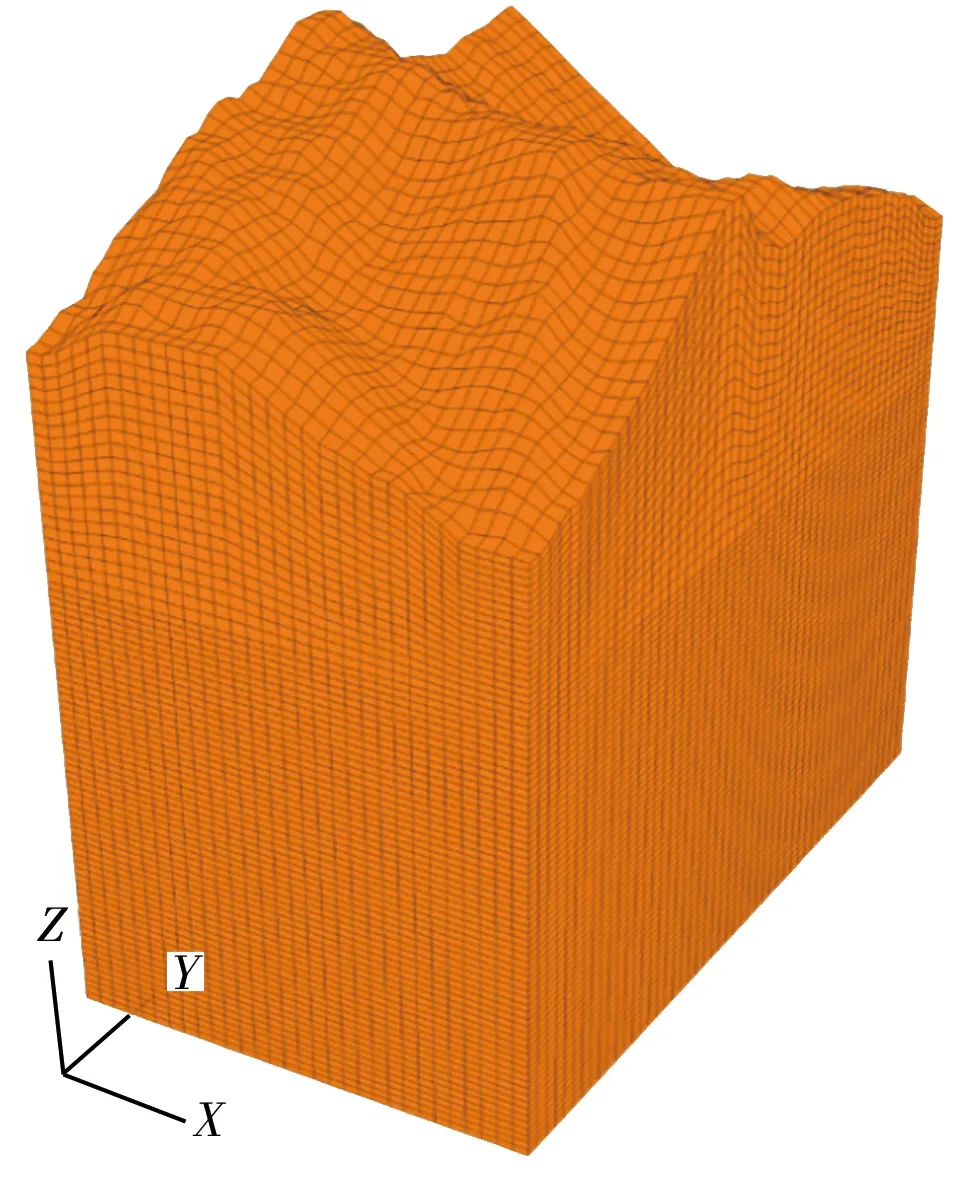
图4 计算网格
2.3 工程区地应力测试成果及初步分析
为了解工程沿线深埋段初始地应力情况,在工程可行性研究阶段,本工程勘察设计单位采用水压致裂法对线路深埋段进行了地应力测量,对输水隧洞深埋洞段的地应力场有了基本认识。计算范围内进行地应力测试的钻孔为FSGZ24号孔,孔口高程963.1 m,孔深888.8 m。根据测孔岩芯判别,在岩体相对完整的深度区间进行水压致裂测试,成功获得18段测试数据,对其中具有代表性的5个测段进行最大水平主应力的方向印模,测试成果见表2。
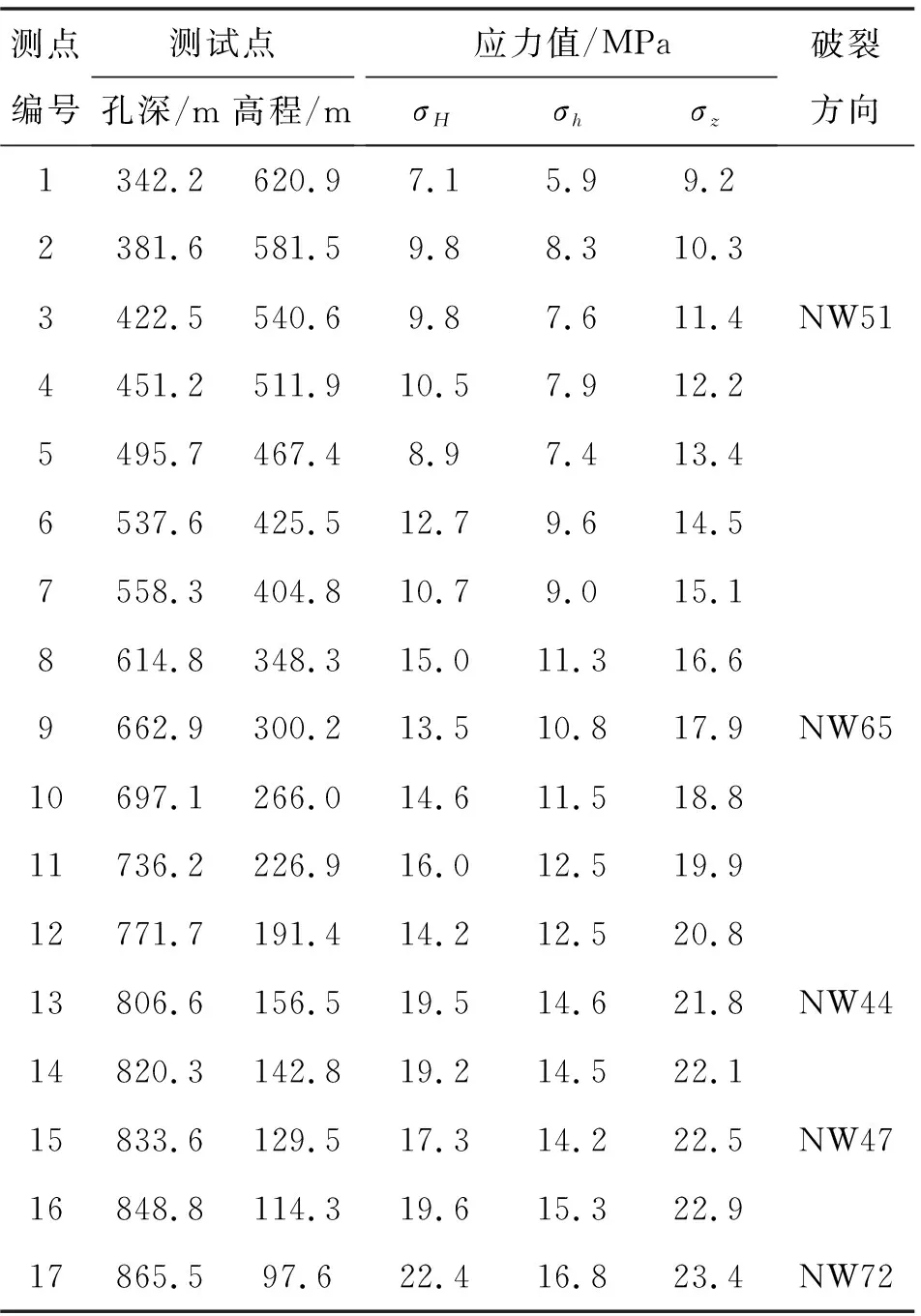
表2 FSGZ-24钻孔水压致裂法地应力测试结果
由实测地应力成果可知,在孔深342.2~882.2 m(高程80.9~620.9 m)范围内,最大水平主应力为7.1~22.4MPa,最小水平主应力为5.9~16.8 MPa,自重应力为9.1~23.4 MPa。最大水平主应力方向的侧压系数(σH/σz)为0.7~1.0,3个主应力主要呈σz>σH>σh特征,说明该区地应力场以自重应力为主。依据压裂缝方向印模结果,钻孔最大水平主应力方向稳定在N44°W~N72°W。测试方向比较一致,主要呈NW—NWW。
水平主应力的大小与孔深关系见图5。可以看出,除了局部测点,测试结果总体沿孔深增加而增大,应力测试数据与深度的拟合关系见式(4):
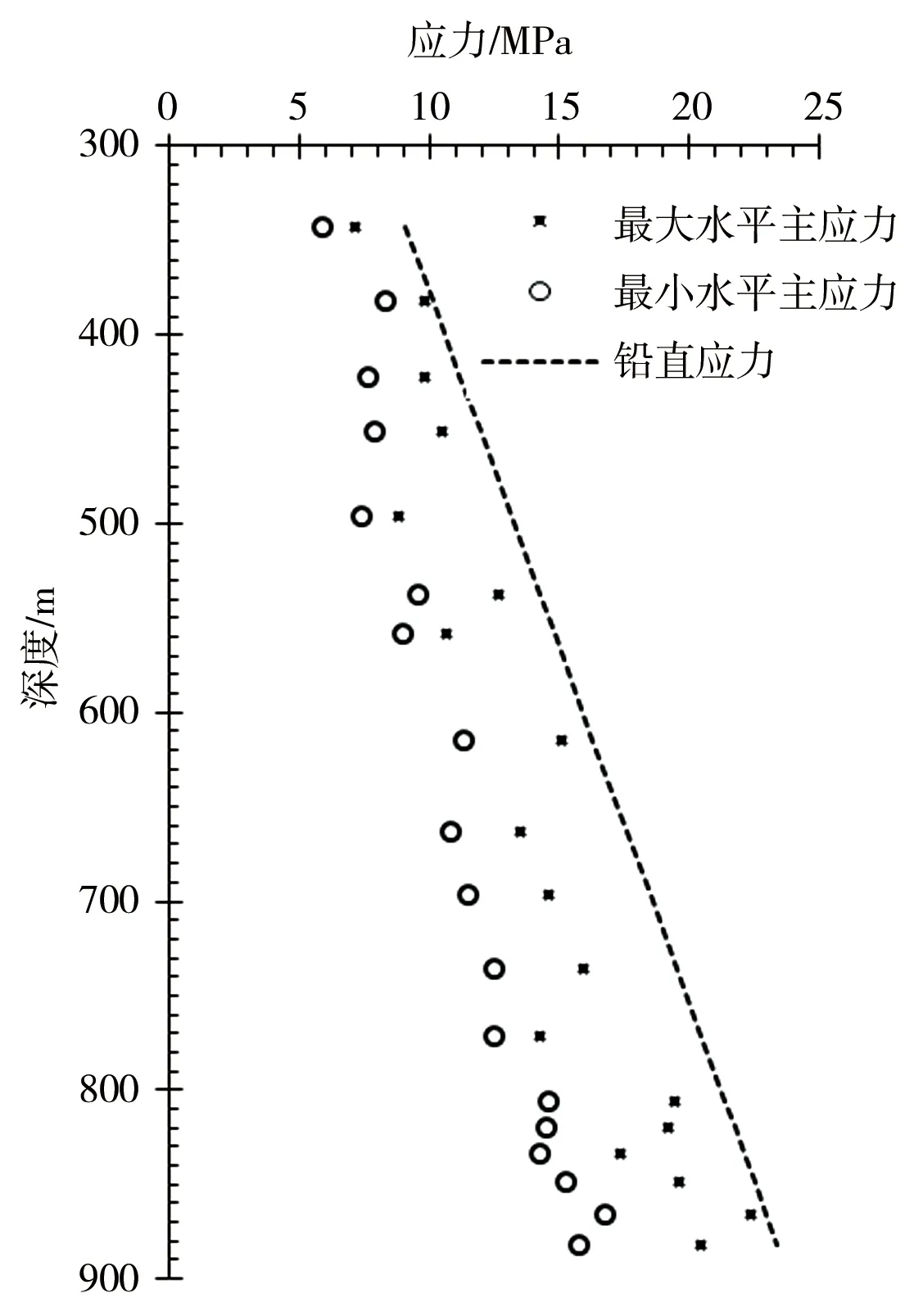
图5 FSGZ-24钻孔的主应力量值与孔深关系
(4)
由于建立模型划分网格的精细程度所限,部分计算监测点与实测地应力位置偏差较大,为确保实测数据的可靠性,剔除与模型计算监测点位置偏差较大测点,选取以下13个点作为反演计算区域内初始地应力场的依据,并根据弹性力学理论,将实测地应力值转成计算坐标系下地应力实测值(表3)。
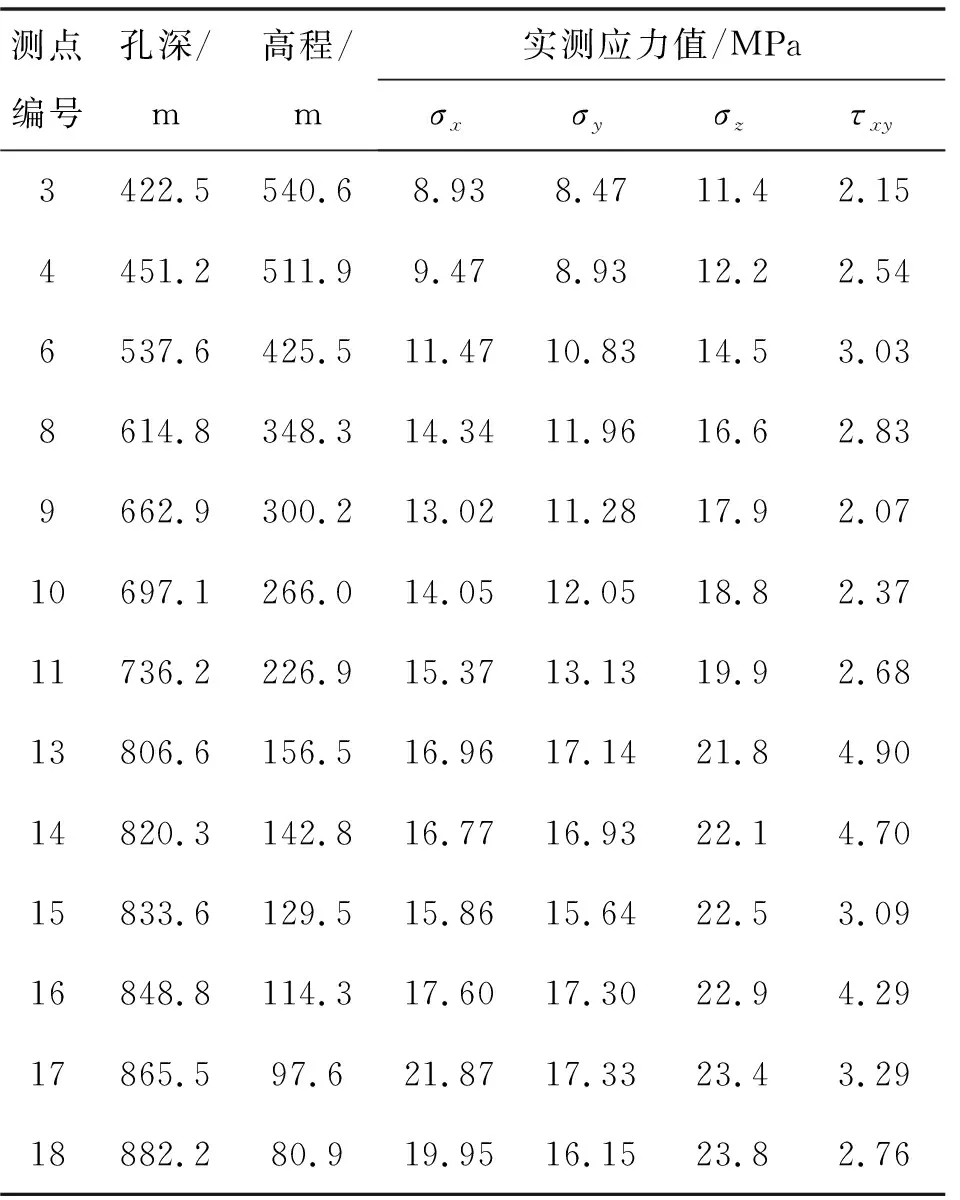
表3 计算坐标系下地应力实测值
3 反演计算及结果分析
三维模型建立之后,按自重作用、X向挤压、Y向挤压、XY平面内水平剪切、XZ垂直平面内剪切、YZ垂直平面内剪切6种因素单独作用分别进行模拟计算,在6种工况下沿隧洞轴线方向垂直剖面上的最大最小主应力情况见图6—11。在计算过程中,在实测地应力点处设置计算监测点,监测在各因素作用下的地应力计算值。
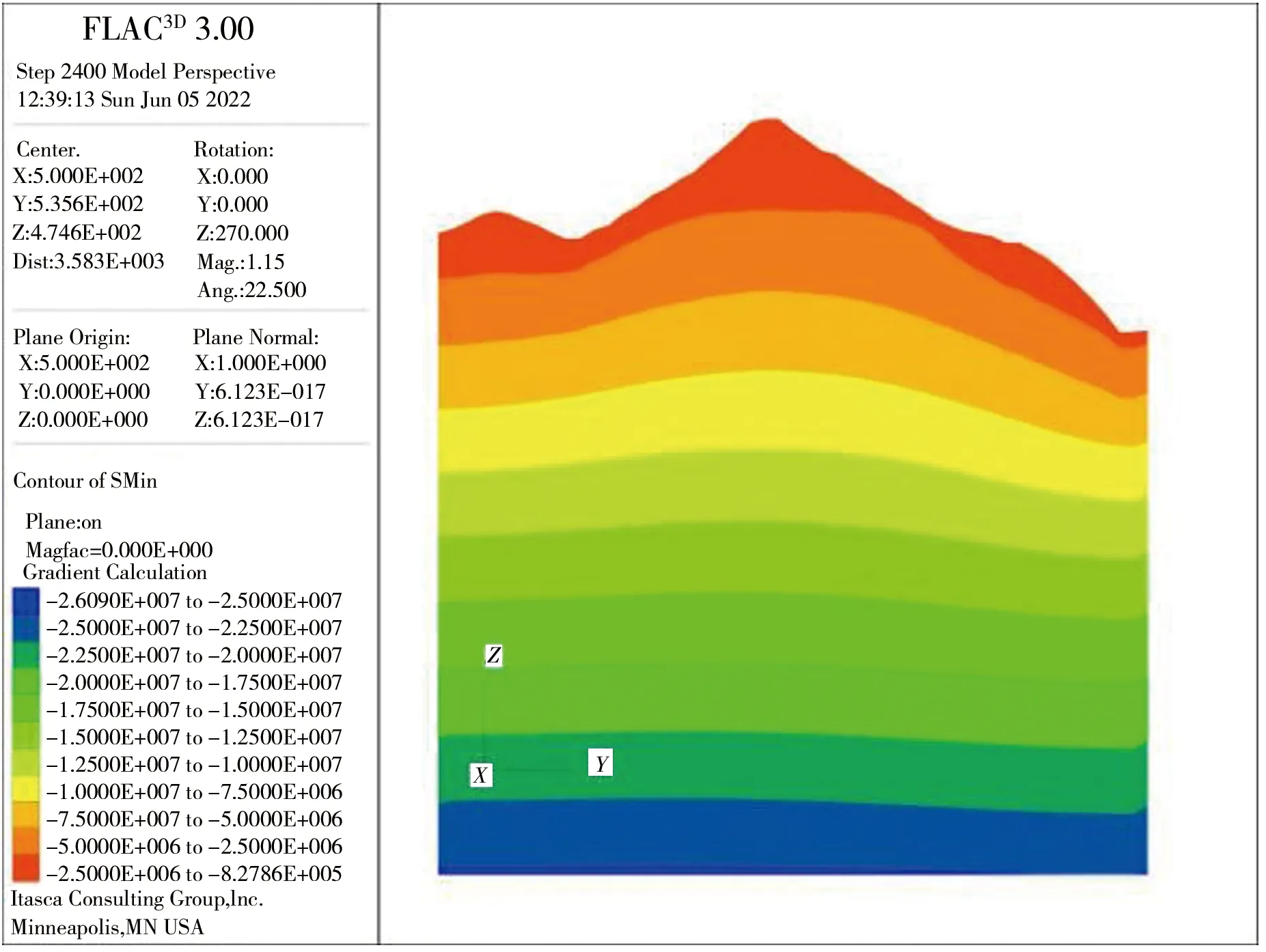
a)最大主应力
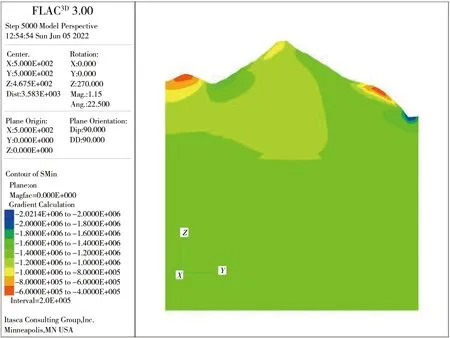
a)最大主应力
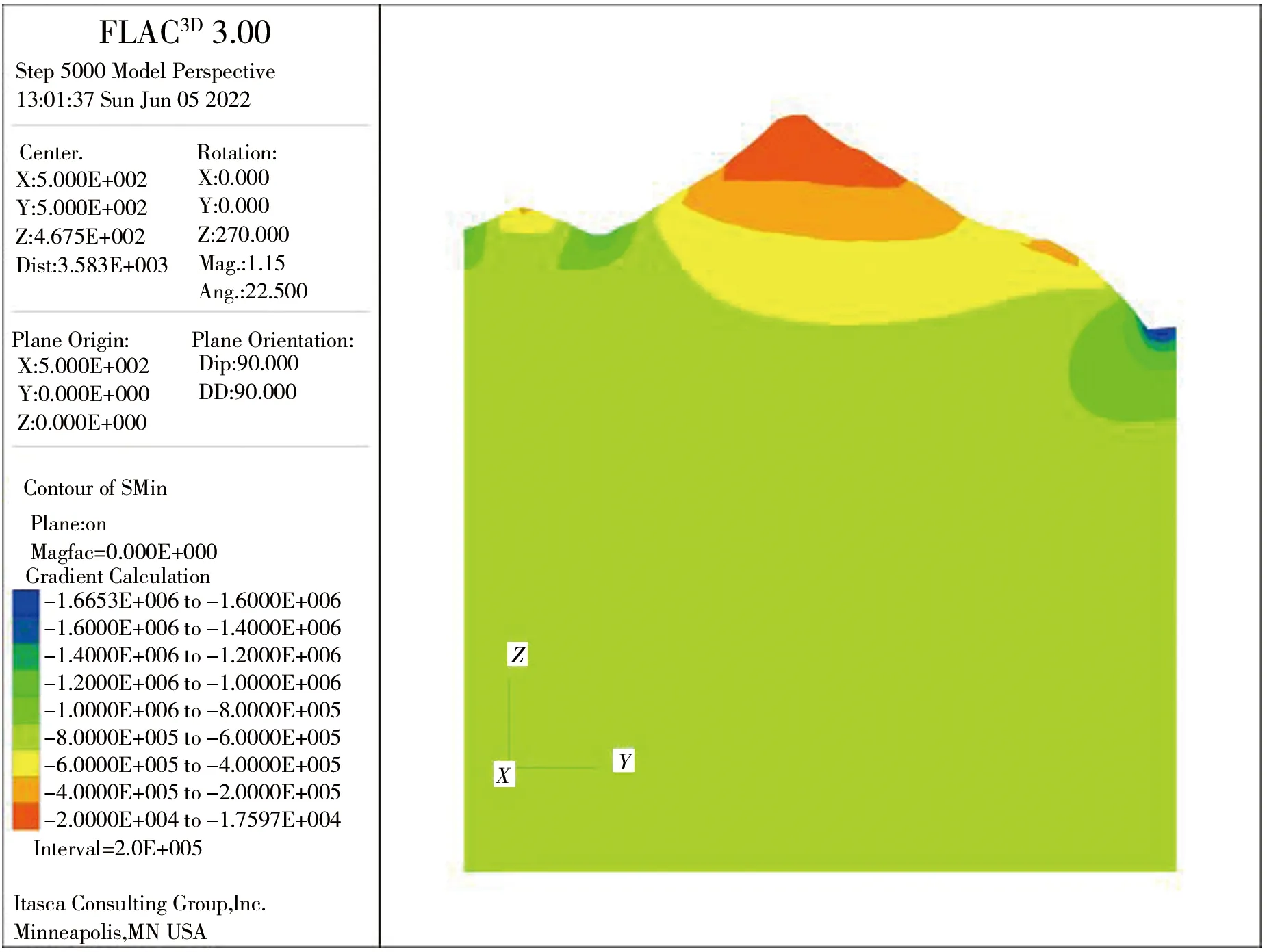
a)最大主应力
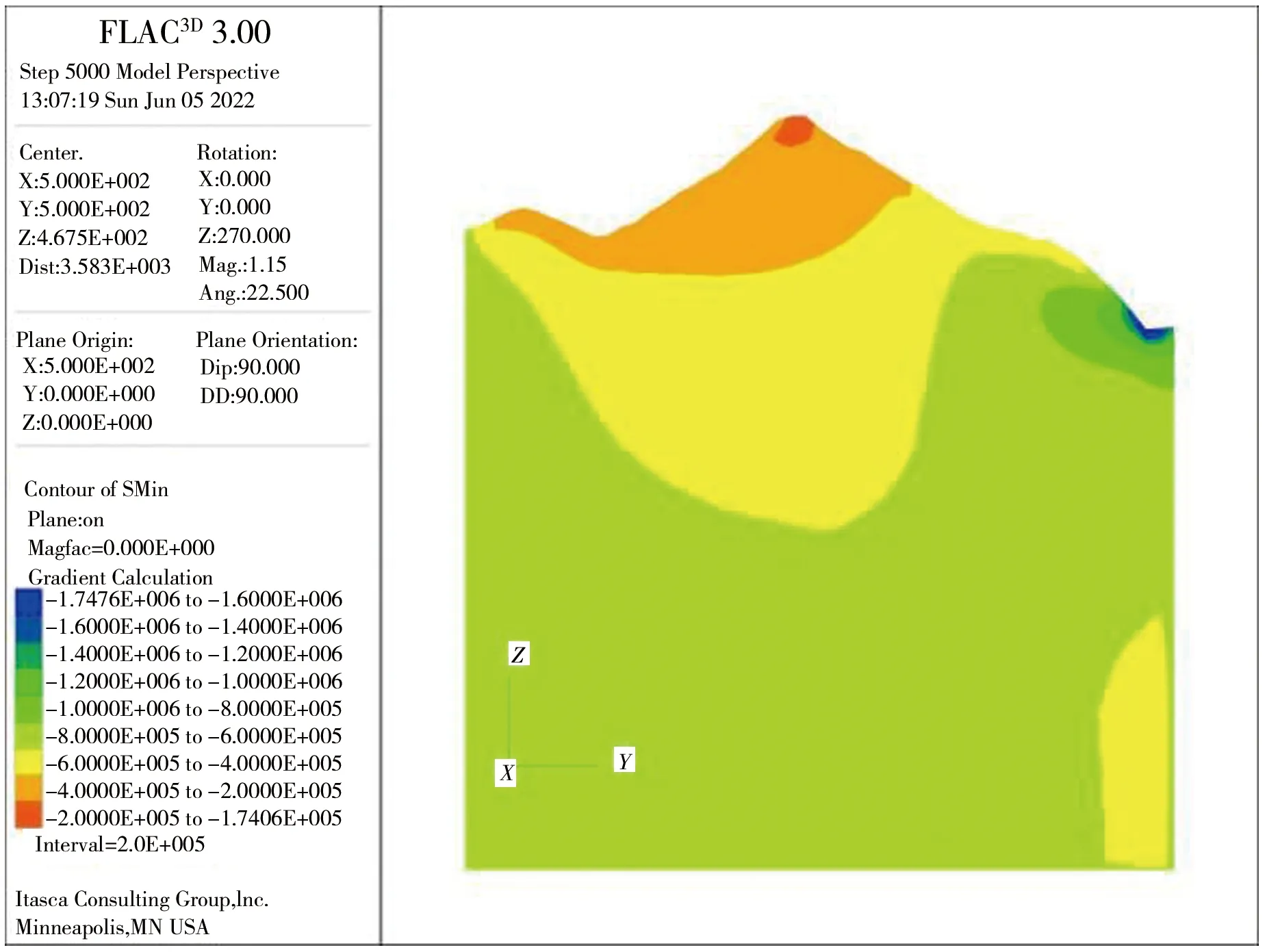
a)最大主应力
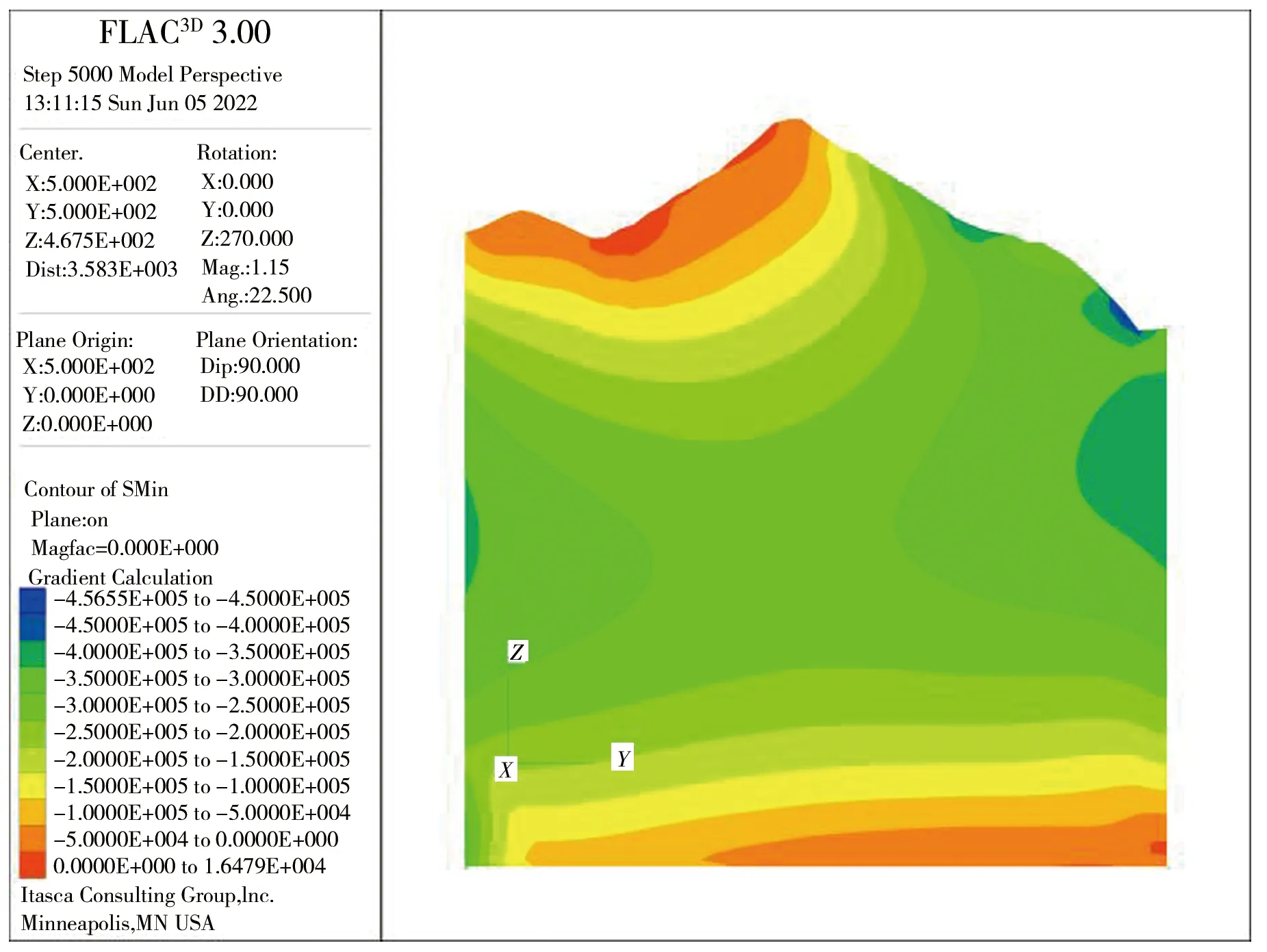
a)最大主应力
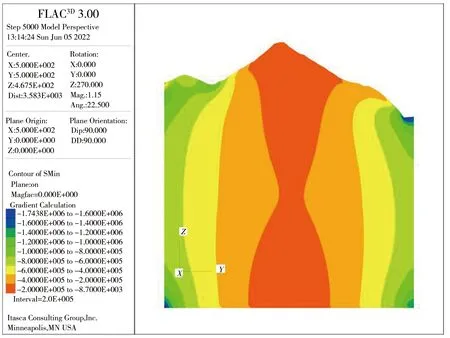
a)最大主应力
3.1 线型回归分析步骤
步骤一:采用最小二乘法进行多元线型回归确定回归方程的系数。
步骤二:通过F检验是判断是否存在显著的线性关系。
步骤三:通过决定系数R2值分析模型拟合情况,同时对VIF值进行分析,确定模型的共线性。
步骤四:分析其显著性。
步骤五:确定模型公式(图12)。
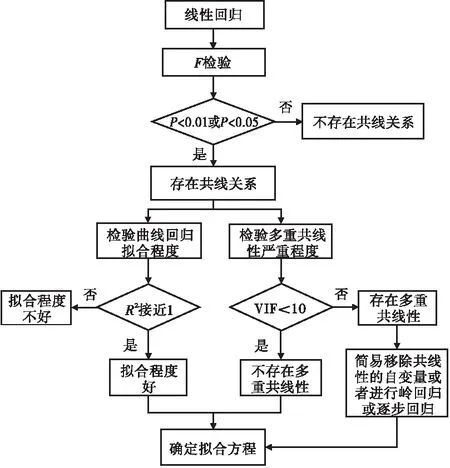
图12 回归分析流程
3.2 线性回归分析结果
对图2中确定的 6 种工况利用 FLAC3D分别进行模拟计算,然后以实测地应力结果(表2)在计算坐标系下的应力分量(表3)为回归目标。利用最小二乘法进行多元线性回归,求得6个自变量的回归系数L1=1.275,L2=8.968,L3=2.247,L4=-7.113,L5=-85.48,L6=185.77,观测误差εk=3.71。曲线回归的拟合程度R2=0.991,表明回归公式的相关性较好。则该工程区初始地应力场回归方程为:
σd=1.275σz+8.968σx+2.247σy-7.113τxy-85.48τxz+185.77τyz+3.715
从F检验的结果分析可以得到,显著性P<0.001,水平上呈现显著性,因此模型基本满足要求,对于变量共线性表现显著度检验观测值F=830.123,可以认为该 6个自变量的总体效果显著。
通过应力场平衡计算,得到计算坐标系下各测点的回归应力值,测点的地应力实测值与回归主应力值对比见图13。
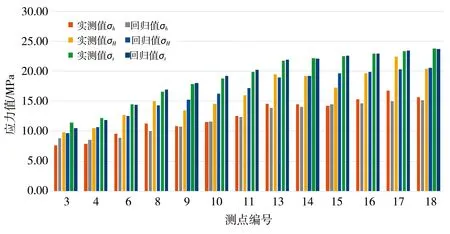
图13 地应力实测值与回归值对比直方
3.3 初始地应力重构
根据线性回归系数及各工况构造相应模型重构研究区域初始地应力模型,从而得到工程区任意一点的地应力状态。各种工况叠加过程中,需要及时调整边界条件。各工况叠加顺序及约束条件如下。
a)自重应力,约束X向两侧边界的X向位移、约束Y向两侧边界的Y向位移、约束底部边界的Z向位移。
b)X向挤压,释放X向一侧边界约束,并添加X向速率。
c)Y向挤压,清除X向速率,重新约束X向侧边界,释放Y向一侧边界约束,并在此添加Y向速率。
d)XY向剪切,清除Y向速率,释放X向及Y向两侧约束,分别在X向两侧添加大小相同、方向相反的Y向速率,在Y向两侧添加大小相同、方向相反的X向速率。
e)X向垂直平面内剪切,释放底部Z向约束,清除X向及Y向速率,在X向两侧添加X向约束,在Y向两侧添加Y向约束,在X向两侧分别添加大小相同、方向相反的Z向速率。
f)Y向垂直平面内剪切,清除Z向速率,在Y向两侧分别添加大小相同、方向相反的Z向速率。
按以上逐步叠加6种工况并进行运算,各测点反演值及实测值对比见表4。
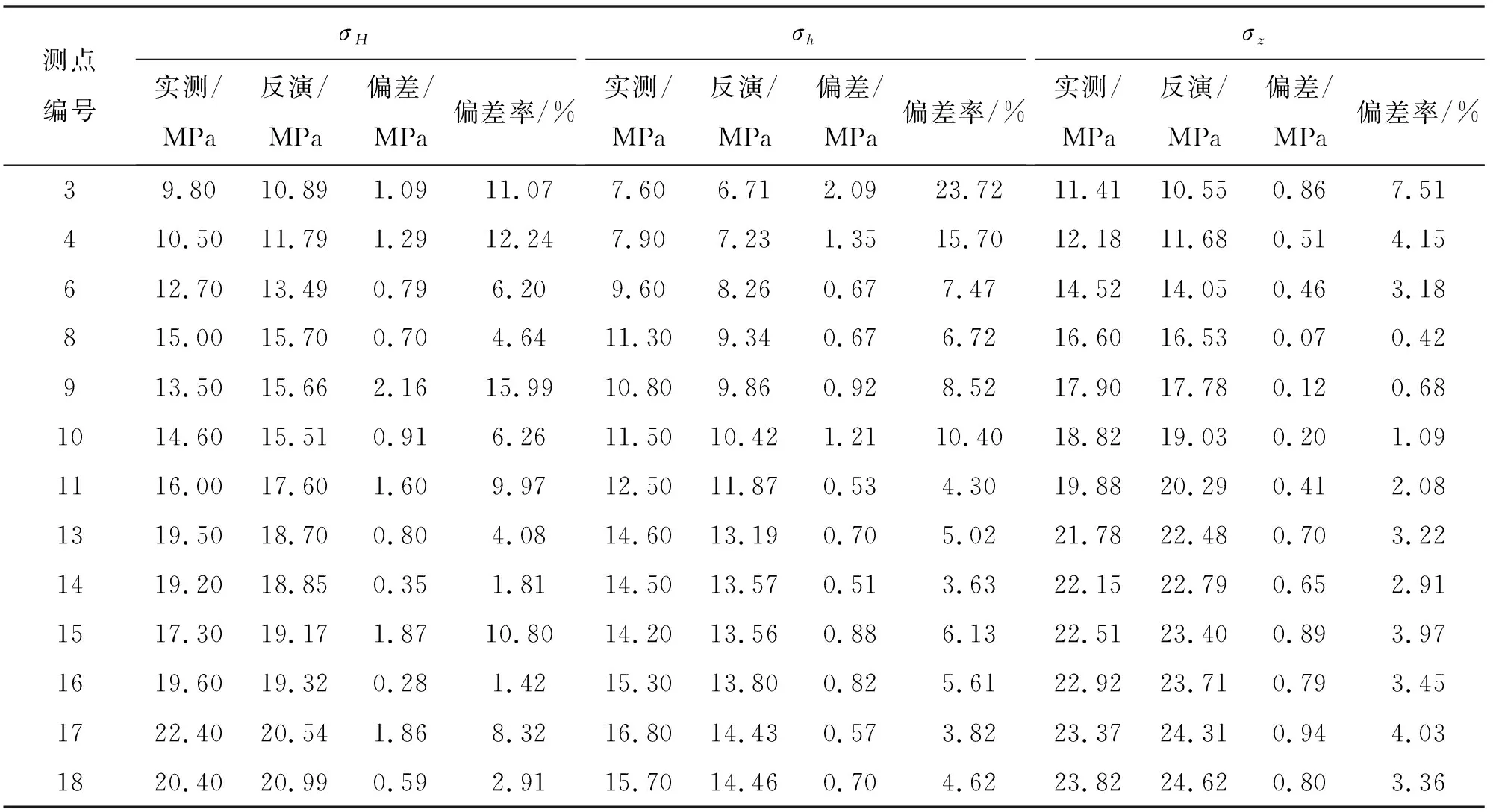
表4 各测点实测地应力值与反演值对比
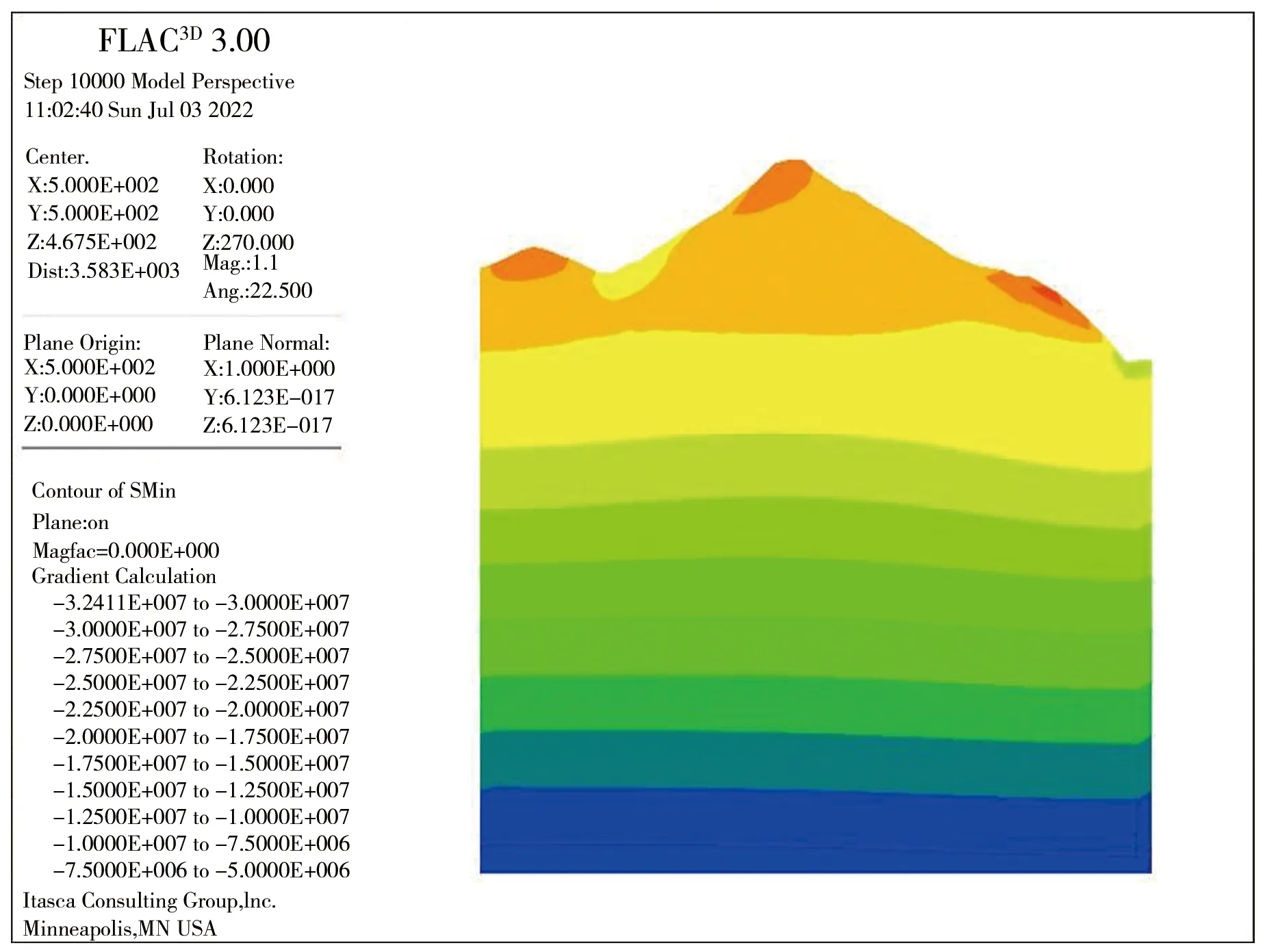
a)最大主应力
3.4 结果分析
由图13、14及表4可以看出,回归结果、反演结果与实测结果基本吻合,反演水平最大主应力方向为N46°W~N54°W,实测地应力最大水平主应力方向为N44°W~N72°W,反演结果与实测结果符合程度较好,说明本次反演较好地模拟了该工程区初始地应力场分布情况。埋深较小处地应力大小受地形起伏影响较大,随着埋深的逐渐增大,初始地应力分布受地形影响越来越小。
4 结论
a)基于最小二乘法的多元线性回归,采用有限差分软件FLAC3D进行反演分析本工程的初始地应力场分布,反演值与实测值拟合程度较好,可为工程设计及施工提供有意义的初始地应力数据。
b)实测最大水平主应力方向的侧压系数(σH/σz)为0.7~1.0,反演分析最大水平主应力方向的侧压系数(σH/σz)为0.81~1.00,且3个主应力均呈σz>σH>σh特征,说明该区地应力场以自重应力为主。
c)实测最大水平主应力方向为N44°W~N72°W,反演水平最大主应力方向为N46°W~N54°W;反演区域输水隧洞走向为S30°W,根据实测成果,隧洞走向与最大水平主应力方向夹角为74~102°,根据反演结果,隧洞走向与最大水平主应力方向夹角为76~84°,均为大角度相交,这对隧洞围岩稳定性不利,隧洞开挖时,两侧洞壁存在较为突出的稳定性问题,支护设计时应予以考虑。
d)由反演成果可知,地表凹陷处应力集中明显(图14),随着埋深的加大,地形起伏对地应力分布的影响逐渐减小,应力集中现象逐步消失,地应力分布趋于平稳。鉴于此种情况,对于自重应力为主的深埋工程,在建立三维地质模型进行数值模拟分析时,可以根据实际情况对地质模型进行适当简化,如不考虑地形起伏对分析成果的影响,可以极大降低模型建立的难度。
