不同导叶张数对双向竖井贯流泵装置影响的受力分析
2023-04-19林鹏程柏周汤方平张烨栋郑彬汪勇
林鹏程,柏周,汤方平*,张烨栋,郑彬,汪勇
不同导叶张数对双向竖井贯流泵装置影响的受力分析
林鹏程1,柏周2,汤方平1*,张烨栋3,郑彬3,汪勇4
(1.扬州大学 水利科学与工程学院,江苏 扬州 225000;2.江苏省沭阳县水利局,江苏 宿迁 223600;3.浙江省钱塘江流域中心,杭州 310020;4.浙江水利水电建设控股发展公司,杭州 310020)
【目的】研究竖井贯流泵装置在不同导叶片数影响下的受力情况。【方法】本文采用CFD方法,以某工程双向竖井贯流泵装置为研究对象,利用TurboGrid和Icem进行网格划分,基于RNG湍流模型,对4、5、6、8片导叶片数的双向泵装置在-2°安装角度下分别取0.85、、1.15的流量工况进行数值计算和试验研究。【结果】正反向运行情况下,导叶片数为4、5、6、8片的情况下泵装置轴向受力平均值接近,当导叶片数与叶片数成倍数关系时,轴向力脉动峰值显著增大,影响装置安全运行;叶轮径向受力均较小,可以忽略对工程的影响。将导叶片数设置为偶数时,可降低导叶受到的径向合力。【结论】在实际设计生产过程中,应当避免使导叶片数与叶片数成倍数关系。
导叶片数;受力分析;双向竖井贯流泵装置;数值模拟;模型试验
0 引言
【研究意义】近年来,由于跨流域调水和农业灌溉等方面的需求[1-2],国内建成了大批的双向竖井贯流泵站,这种泵站同多数水力机械一样为可逆机械,可正反向运行。但在运行过程中,泵站经常受到产生振动等一些问题[3],其中受力不稳定是造成泵装置破坏的直接原因[4]。因此有必要对不同导叶片数泵装置叶轮和导叶所受到的轴向力、径向力和扭矩进行研究。
【拟解决的关键问题】本文探究导叶片数对双向贯流泵装置的轴向受力情况的影响,并分析不同导叶片数对泵装置径向受力的影响。采用小流量(0.85)、设计流量()和大流量(1.15)3种工况下进行非定常数值计算,通过数值模拟计算,分析叶片数在全程流量工况下对泵装置的受力影响。
1 数值模拟
1.1 计算模型
双向竖井贯流泵装置包括竖井流道、叶轮、导叶、导水锥和直管流道,模型如图1所示。其中叶轮的直径=300 mm,叶顶间隙=0.2 mm,叶轮叶片数(ZR)4片,导叶片数()采用4个方案,分别为4、5、6、8片,模型正向转速为1 196 r/min,反向转速为1 303 r/min。
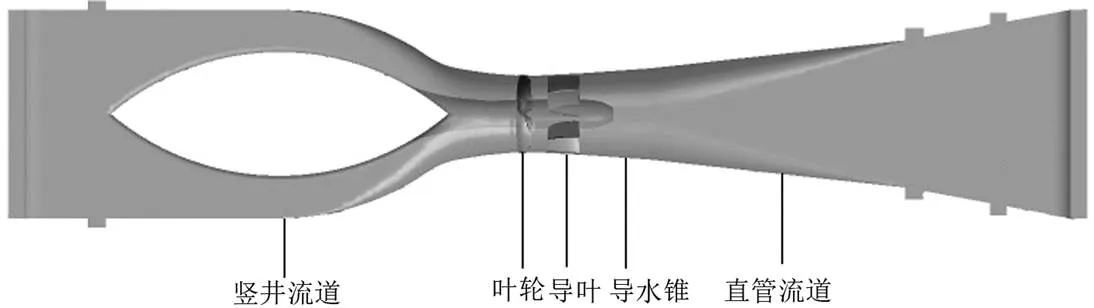
图1 泵装置计算模型
1.2 数值计算与网格划分
由于计算精度受网格质量的影响较大,本文的叶轮室以及导叶体采用ANSYS Turbo Grid软件进行网格划分,网格为结构化网格,如图2所示,其中图2(a)为叶轮网格,图2(b)为=5时导叶体网格。其余部件采用mesh绘制非结构化网格,并保证网格质量在0.3以上,分别如图2(c)和图2(d)所示。边界层附近的流动计算利用近壁面Blasius公式来处理:
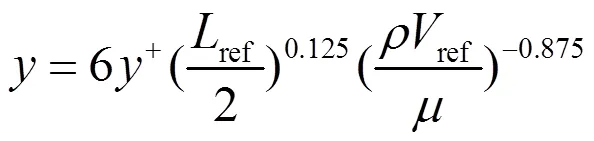
式中:y为固体壁面外第一层网格的厚度(m);y+为无量纲参数;Lref为参考长度(m);Vref为参考速度(m/s);ρ为液体的密度(kg/m3);μ为液体的动力黏度(Pa/s)
现对网格进行无关性分析。以全装置网格数330万作为初始模型,通过增加网格的数量进行网格无关性分析。由于导叶叶片数不同时,导叶的网格数也会有所差异,保持导叶网格数在120万个左右。如图3所示,当装置总网格数在580万个以上时,泵装置效率上下浮动不超过1%,可以认为满足计算精度的要求,因此以网格总数629万为计算模型,详细数据如表1所示。
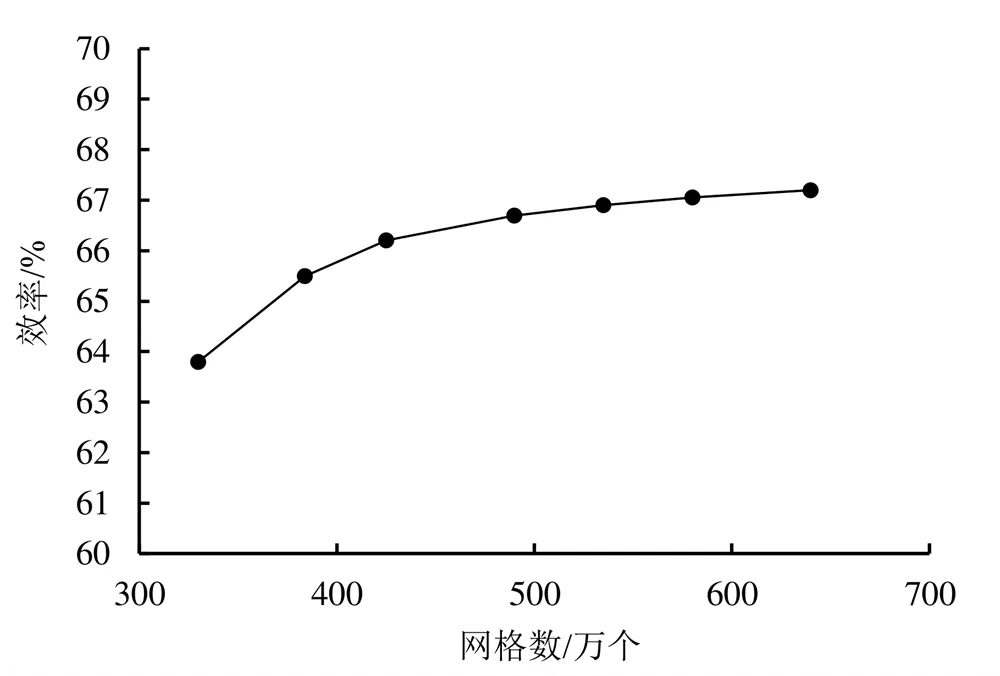
图3 网格无关性分析

表1 泵装置各部分节点数与网格数示意表
1.3 计算设置及边界条件设置
本文在三维网格上通过数值计算求解时间平均的雷诺方程及RNG k-ε紊流模型来得到泵装置的水力性能及内部流场。最大迭代步数为2 000步,收敛精度为1.0×10-5。对于边界条件,进口条件采用压力进口,取1.0×106Pa;出口条件采用恒定质量流量出口,壁面边界条件采用无滑移边界条件(即===0)。进水流道与叶轮进口、叶轮出口断面和导叶进口断面之间的动静交界面采用“Stage”技术来处理。导叶与导水锥之间的静静交界面采用设置为None。
1.4 非定常计算设置
对双向竖井贯流泵装置正反向在小流量(0.85)、设计流量()和大流量(1.15)3种工况下进行非定常数值计算。计算设置中,进口条件采用压力进口,取1.0×106Pa;出口条件采用质量出口,给定出口边界上的质量流量;在固体边壁处采用无滑移边界条件(即===0)。进水流道与叶轮进口、叶轮出口与导叶进口之间的动静交界面采用瞬态冻结转子(Transient Rotor Stator)技术来处理。导叶与导水锥等之间的静静交界面采用设置为none。设置单步步长为叶轮旋转1°所需要的时间,每个时间步长内最大迭代步数设置为20步,单步收敛精度为1×10-5。叶轮旋转一周有360°,共有8个周期,正向所需要的总时间为0.401 34 s,反向所需要的总时间为0.368 38 s。非定常计算模型采用sst模型,以定常结果作为初始条件进行非定常计算。
2 材料与方法
2.1 试验模型简介
根据数值模拟结果,利用钢板将进出水流道加工成型,导叶采用实验室配套导叶。泵装置模型试验及压力脉动试验在扬州大学测试中心的高精度水力机械试验台上进行。该试验台示意图见图4。
2.2 数值模拟的可靠性分析
为了验证泵装置数值模拟是否可靠,采用5片和6片导叶,将泵装置在叶片角度为0°时进行模型试验,并将试验结果与数值计算结果对比,如图5所示。
由图5可知,当流量小于设计流量的情况下,数值模拟的效率略低于试验结果,在大流量的工况下,数值模拟结果与试验结果贴合较好。二者最大差异不超过3%,整体结果吻合较好,说明数值分析结果可以较好反应内部流场情况。
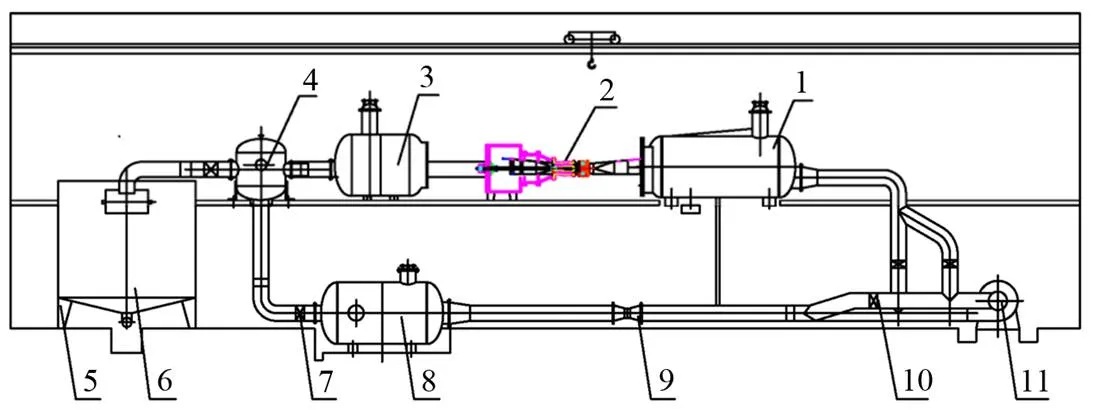
注 1.进水箱;2.受试泵装置及驱动电机;3.压力出水箱;4.分叉水箱;5.称质量传感器;6.原位标定装置;7.调节闸阀;8.稳压整流筒;9.电磁流量计;10.控制闸阀;11.辅助泵机组
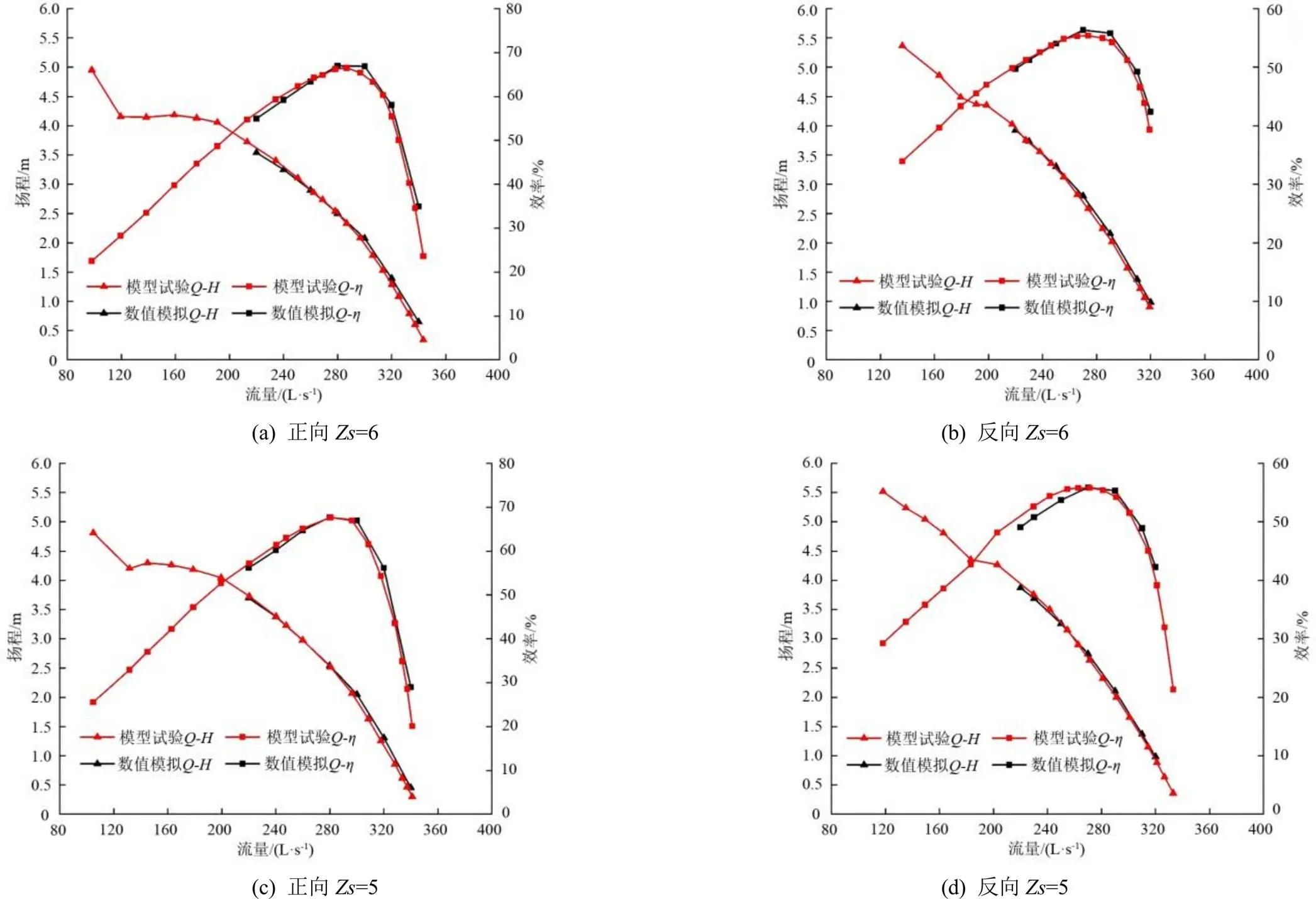
图5 Zs=6与Zs=5时模型试验与数值模拟对比
3 结果与分析
3.1 不同导叶片数正向运行时泵装置叶轮受力分析
首先定义空间固定坐标系O-XYZ,其中轴与叶轮轴线一致,方向以水流方向为正,如图6所示。
在不同工况下不同导叶片数叶轮所受到的轴向力和径向合力如表2所示(为叶轮旋转1周内轴向力的平均值;为叶轮旋转1周内径向合力的平均值。方向以正向水流方向为正。)。
图6 空间固定坐标系
由表2可知改变导叶片数对叶轮所受到的轴向力和径向合力的影响都不大,在导叶片数相同的情况下,叶轮受到的径向力和轴向力的大小随着流量的增大而逐渐减小,这是由于随着流量增大,叶片的吸力面和压力面之间的压力差逐渐减小,从而使得轴向力的减小。同时随着流量增加,流动变得稳定,径向力也因此减小。在同一工况下,当=5时,叶轮径向合力最大。在泵装置运行过程中,叶轮所受到的径向力远小于轴向力,所以其影响可忽略。

表2 正向运行时叶轮的轴向力和径向合力
仅仅对叶轮受力平均值的研究无法分析出叶轮不同导叶片数下的差异,现分别取出在设计工况下不同导叶片数叶轮瞬态轴向力和径向合力,并将其转换成极坐标下的受力分布,从而进一步了解导叶片数对叶轮受力的影响,
首先,取出设计工况下不同导叶片数叶轮瞬态轴向力变化时域图如图7所示。
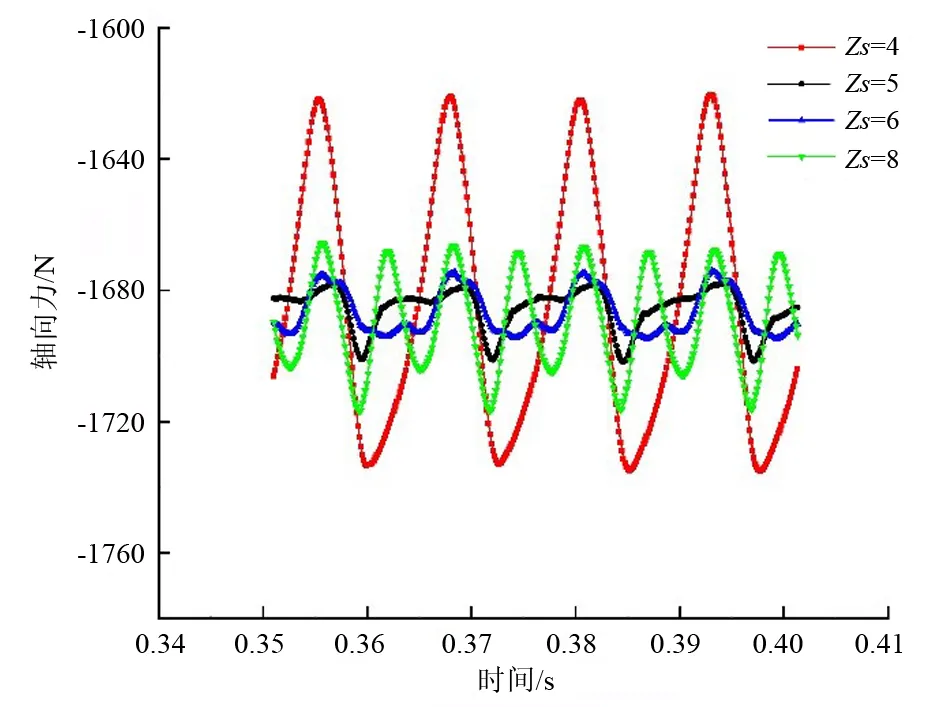
图7 不同导叶片数正向叶轮轴向力时域
虽然叶轮受力的平均值在不同导叶的情况下相差不大,但在时域图中可以明显看出其中差异,在=4时,叶轮所受的轴向力在1个周期内形成了4个标准的正弦波形,波峰与波谷的表现明显;当=5和=6时二者曲线形象比较接近,出现4个波峰,且波形已不再规则;当=8时,出现了8个周期的波形,周期数等同于导叶片数,且波形较规则。可见导叶片数的确对叶轮轴向受力有所影响,当=4时受力变化幅度最大,=8时其次,=5与=6的时候轴向力的变化幅度较小且二者波形相似。
不同导叶片数叶轮所受轴向力脉动峰值进行比较。当=4时,叶轮轴向力脉动峰值为113 N;当=5时,峰值为23 N;当=6时,峰值为20 N;当=8时,峰值为40 N。从理论上来说,当叶轮和导叶互质时,即=5时,能够稳定运行。从数值模拟的结果可以看出,当=5和=6时,叶轮所受轴向力脉动幅度均较小;当=8时,叶轮所受轴向力脉动范围变大,峰值约是=5和=6时2倍;当=4时,叶轮所受轴向力脉动范围明显变大,分别是=5和=6时4.91、5.65倍。脉动幅度变大,会引起装置振动、噪声等不良现象,造成材料的疲劳破坏,影响装置的安全运行,因此,导叶片数不应设置为叶轮叶片数的整数倍。
为了分析引起上述差异的原因,取出每个叶轮叶片所受轴向力()随时间的变化规律,并绘制成时域图进行观察分析。
从图8可看出,当=4的时候,4张叶片的受力几乎是同时达到最大值和最小值,这样就使得整个叶轮在1个周期内会有4个明显的波峰与波谷。当=5和=6的时候,4个叶片各自受力的时域图不再相互重合,每张叶片的波峰交替出现,这就使得叶轮整体的受力时域图没有出现明显的波峰与波谷。=6时也是如此。当=8时,不同叶片的波峰与波谷又一次同时出现且频率变为=4的2倍,但这时每个叶片的峰值较低,这使得其叠加之后整体轴向力脉动情况介于=5和=6与=4之间。
在设计工况下不同导叶片数叶轮瞬态径向合力变化时域图,并将其转换成极坐标下的受力分布图8。
图9(a)可以看出,=4和=8的时候二者的时域图和极坐标图中形状相似,产生的径向力也相对较小,当=6时径向力开始变大,当=5时径向力达到最大值。其原因是当=4和=8时,导叶片数与叶片数成倍数关系,水流能够均匀地从导叶各个通道流出,当=5时,导叶片数与叶片数完全互质,使得水流通过各个导叶间的通道情况都不同,使得整体所受径向力波动更大。
由图9(b)的时域图可以看出,在改变导叶片数后,叶轮所受径向合力时域图均存在4个波峰和波谷,与叶片数保持一致。再从整体的幅度来看,此时=5时脉动幅度较大。当=4时,叶轮所受径向合力脉动峰值为0.76 N;当=5时,叶轮所受径向合力脉动峰值为1.76 N;当=6时,叶轮所受轴向力脉动峰值为0.91 N;当=8时,叶轮所受轴向力脉动峰值为0.66 N。在实际工程运行中,要想保持稳定运行状态,叶轮所受到径向力应尽量趋向于0。从数值模拟的结果可以看出,当=5时,叶轮所受径向合力脉动范围变大,当=4和=8时,叶轮所受径向合力脉动均较小;但叶轮所受径向合力及其脉动大小远小于轴向力合力,对泵装置影响有限,在实际工程中可忽略其影响。
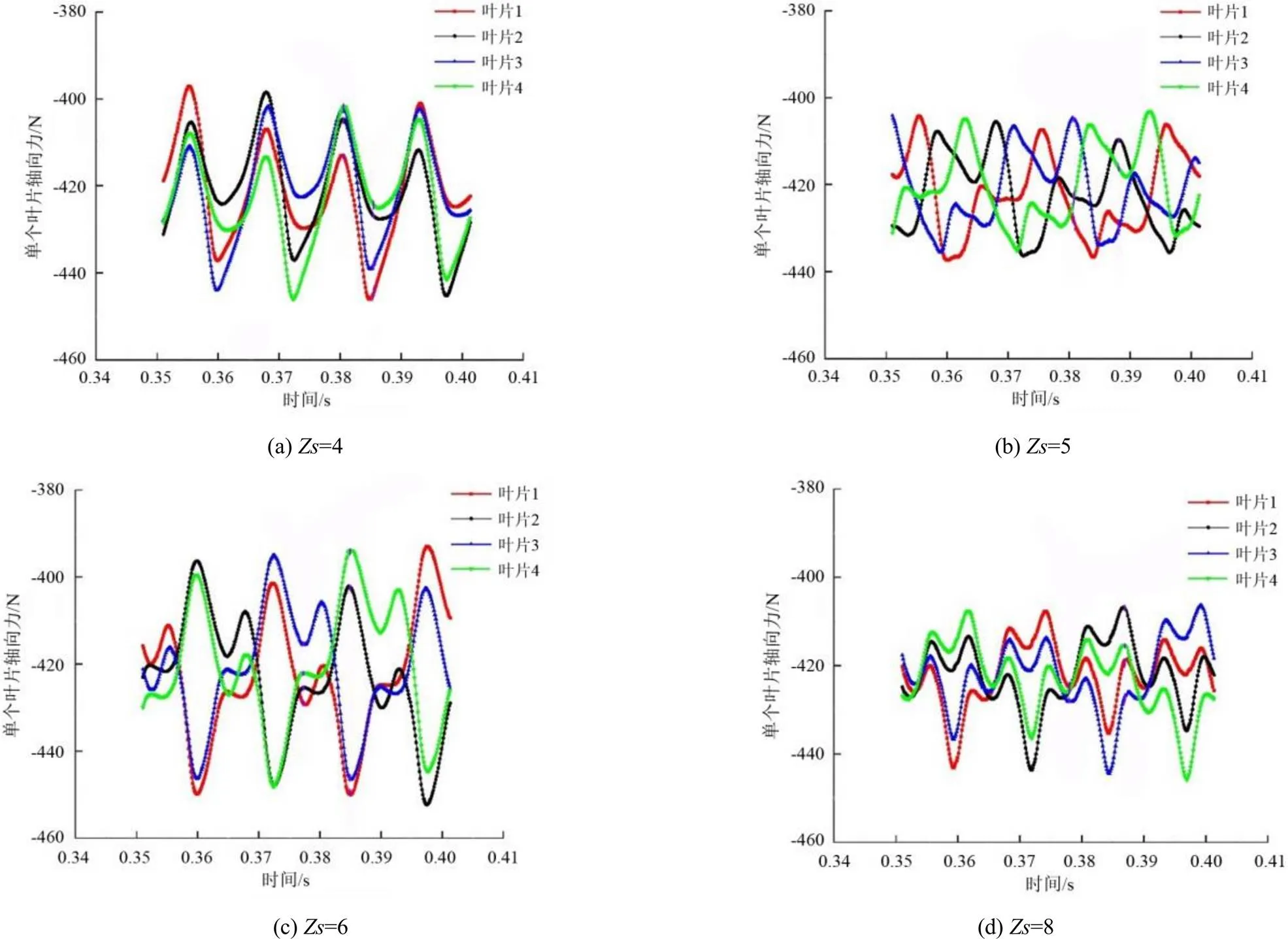
图8 不同导叶片数正向每个叶轮叶片轴向力时域
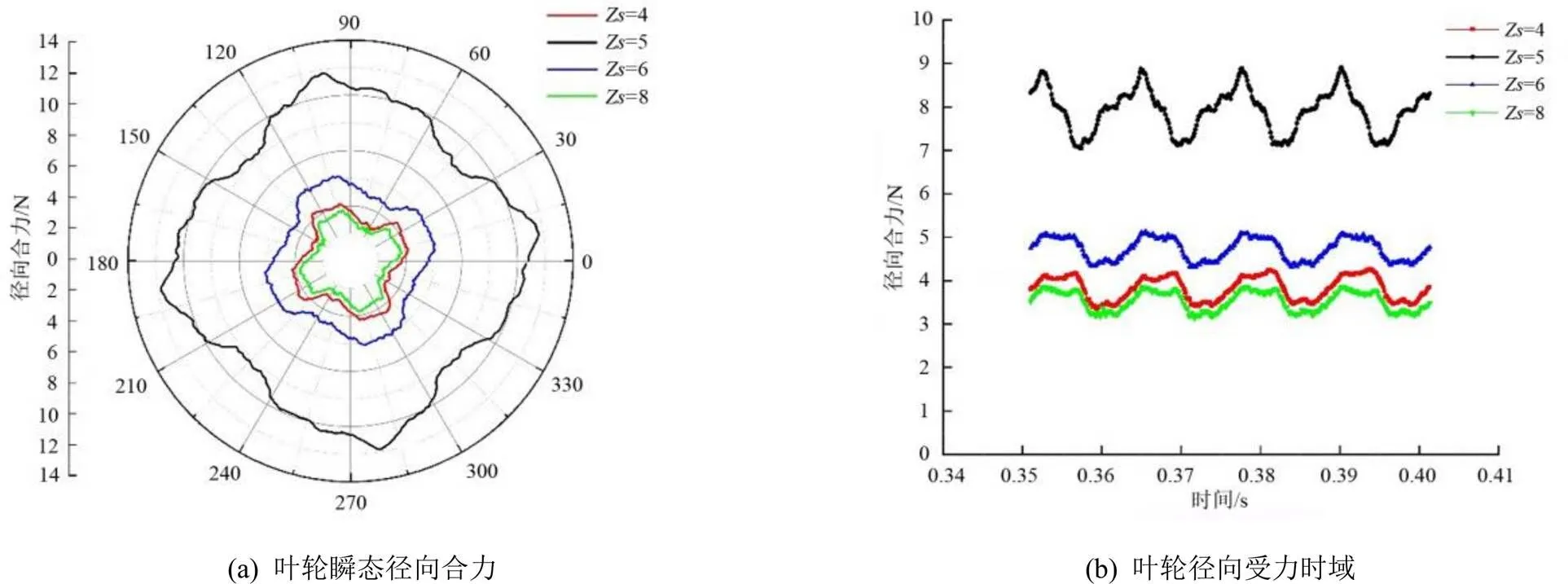
图9 不同导叶片数反向叶轮径向受力分布图
3.2 不同导叶片数反向运行时泵装置叶轮受力分析
不同导叶片数叶轮在不同工况下所受到的轴向力和径向合力从表3可以看出,在同一工况下,随着导叶片数逐渐增大,轴向力逐渐减小。在同一导叶片数情况下,随着流量的增大,轴向力逐渐减小,且不同工况下轴向力差值逐渐增大。在同一工况下,在=5时叶轮所受到的径向合力均最大,说明此时叶轮域内流场压力分配不均,但与轴向力相比,其大小可以忽略。

表3 反向运行时叶轮的轴向力和径向合力
设计工况下不同导叶片数叶轮瞬态轴向力变化时域,如图10所示反向运行时,水流先经过导叶进而流入叶轮,其规律与正向相比有较大差异。
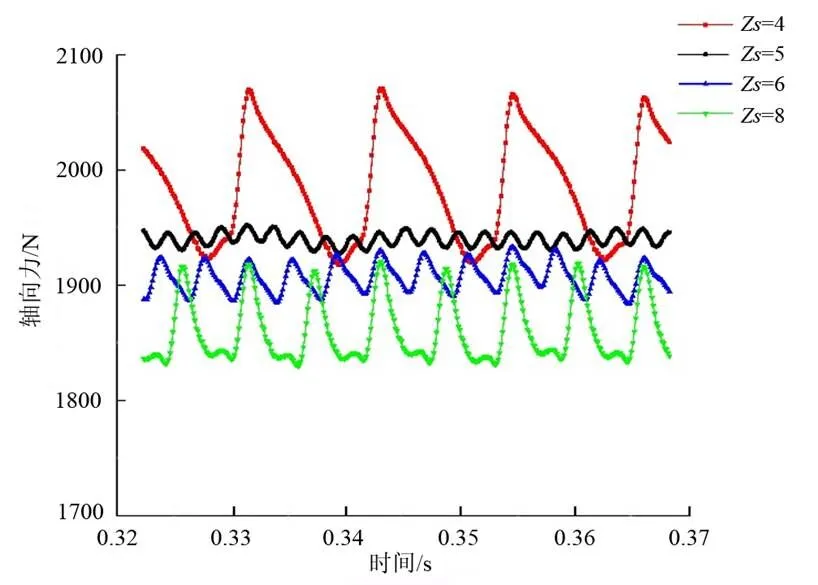
图10 不同导叶片数反向叶轮轴向受力时域
从图10可以看出,当=4时,叶轮旋转1周存在4个周期;当=8时,叶轮旋转1周存在8个周期;当=5时,叶轮旋转1周存在20个周期;当=6时,叶轮旋转1周存在12个周期;叶轮旋转1周其周期数为与的最小公倍数,说明其受到叶轮和导叶的动静干涉的影响。最小公倍数越大,叶轮轴向力脉动频率越高。从图10还可以发现,随着导叶片数增加,叶轮所受轴向力逐渐减小。
当=4时,轴向力脉动峰值为151.2 N;当=5时,脉动峰值为14.3 N;当=6时,脉动峰值为32.5 N;当=8时,轴向力脉动峰值为78.4 N。从数值模拟的结果可以看出,当=5时,叶轮所受轴向力脉动较小;当=6时,峰值约是=5的2.27倍;当=8时,峰值约是=5的5.49倍;当=4时,叶轮所受轴向力脉动范围明显变大,峰值约是=5的10.57倍;当=6时,叶轮轴向力脉动峰值相较于=4和=8较小,而=4和=8时其脉动峰值显著增大,对泵装置会产生不利影响。
由图11可以看出当=4时,不同叶片所受的轴向力的情况相似,叶片所受轴向力的波峰与波谷同时出现,从而使得叠加后生成的轴向力时域图的峰值较大:当=5和=6时,不同导叶所受轴向力的峰值交替出现,从而使得整体受力平稳,=8时与=4时相似,但是各叶片所受的轴向力小于=4时的情况,使得总体受力时域图中的峰值与=4时相比较小。
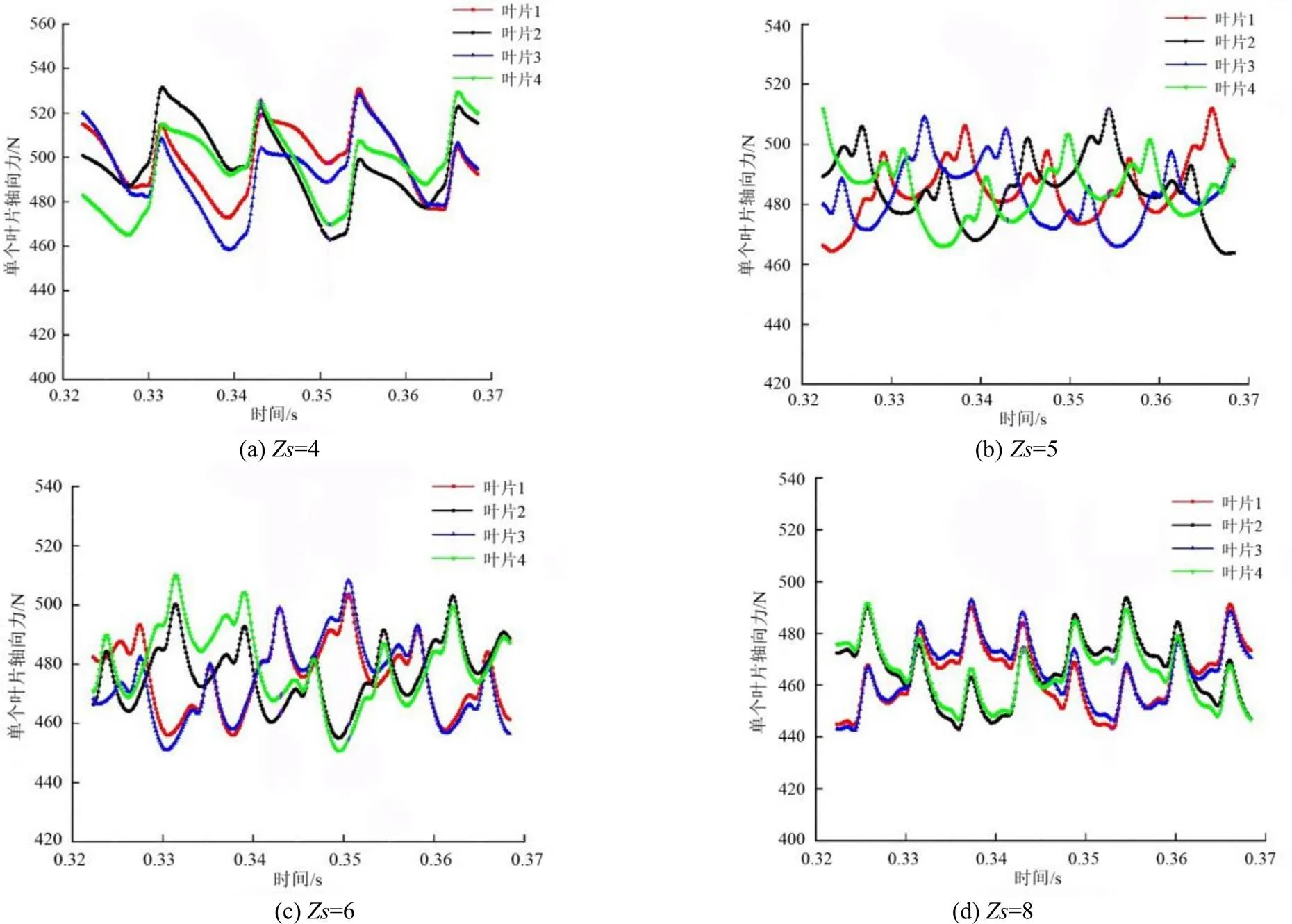
图11 不同导叶片数反向运行时每个叶轮叶片轴向力时域
由图12(a)可以看出,当=4、6、8时,叶轮所受径向合力轨迹相似,大小相近,轨迹线相互重合,与=5的情况有很大区别。=5时,其所受到的径向力相较于=4、5、6时较大,且随着圆周方向出现较大的波动,由图12(b)可以看出,=4、6、8时,三者受径向力规律基本相似,但=5时,径向力叶轮旋转1周的情况下出现了20个周期的波动。
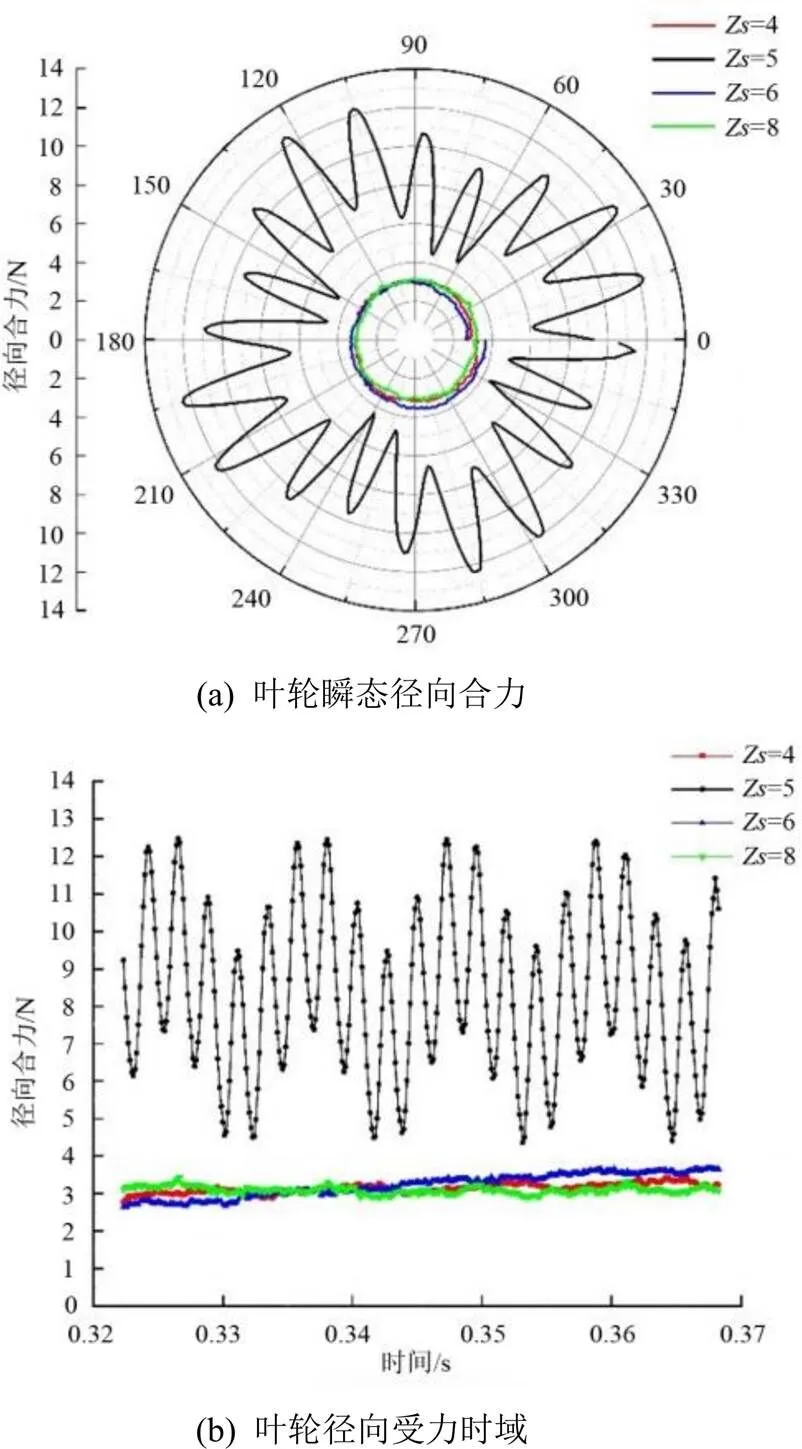
图12 不同导叶片数反向叶轮径向受力分布
从数值模拟的结果来看,当导叶片数为偶数时,泵装置在正、反运行状态下叶轮所受径向合力均比导叶片数为奇数时小。但减小的数值有限,对泵装置的影响可以忽略。
4 讨论
本文通过数值模拟的方式,得到了不同导叶片数双向贯流泵的受力情况,特别是重点分析了轴向力的变化规律和原因。在实际工程应用中,对泵装置受力状态的研究非常重要,因此对于径向力和扭矩的变化原因还有待更深层次的研究。
5 结论
1)数值模拟与物理模型试验的外特性曲线趋势基本一致,数值模拟结果合理可靠,可为相关研究提供参考。
2)正向运行情况下,=4、5、6、8片的情况下泵装置轴向受力平均值接近,当导叶片数与叶片数成倍数关系时,轴向力脉动峰值显著增大,影响装置安全运行。
3)反向运行情况下,泵装置轴向受力平均值随导叶片数增大逐渐减小,当导叶片数与叶片数成倍数关系时,轴向力脉动峰峰值同样显著增大,影响装置安全运行。
4)正反向运行情况下,叶轮径向受力均较小,可以忽略对工程的影响。将导叶片数设置为偶数时,可降低导叶受到的径向合力。
[1] 景瑞, 何希杰. 轴流泵及其应用概述[J]. 通用机械, 2014(9): 86-89.
JING Rui, HE Xijie. Overview of vertical axial flow pump and its application[J]. General Machinery, 2014(9): 86-89.
[2] 刘超. 水泵及水泵站[M]. 北京: 中国水利水电出版社, 2009.
LIU Chao. Pumps &pumping stations[M]. Beijing: China Water Power Press, 2009.
[3] 关醒凡. 现代泵理论与设计[M]. 北京: 中国宇航出版社, 2011.
GUAN Xingfan. Modern pumps theory and design[M]. Beijing: China Space Navigation Press, 2011.
[4] 刘超, 汤方平, 周济人, 等. 大型立式轴流泵装置的性能和稳定性分析[J]. 中国给水排水, 2003, 19(3): 69-71.
LIU Chao, TANG Fangping, ZHOU Jiren, et al. Performance and stability analysis of large vertical axial flow pump[J]. China Water & Wastewater, 2003, 19(3): 69-71.
[5] 郭楚, 郑源, 周大庆, 等. 导叶叶片数及导叶相对位置对低扬程轴流泵装置性能的影响[J]. 排灌机械工程学报, 2019, 37(3): 204-210.
GUO Chu, ZHENG Yuan, ZHOU Daqing, et al. Effects of number and relative position of guide vanes on performance of a low head axial-flow pump device[J]. Journal of Drainage and Irrigation Machinery Engineering, 2019, 37(3): 204-210.
[6] 吴晨晖, 汤方平, 石丽建, 等. 导叶相对距离对S形轴伸式贯流泵压力脉动特性的影响[J]. 水利水电科技进展, 2019, 39(1): 63-69.
WU Chenhui, TANG Fangping, SHI Lijian, et al. Effect of relative position of guide vanes on pressure pulsation characteristics of a S-shaped extension tubular pumping system[J]. Advances in Science and Technology of Water Resources, 2019, 39(1): 63-69.
[7] 李琪飞, 张正杰, 权辉, 等. 水泵水轮机空化流及转轮轴向受力分析[J]. 太阳能学报, 2020, 41(3): 192-198.
LI Qifei, ZHANG Zhengjie, QUAN Hui, et al. Analysis on cavitating flow and axial force in pump-turbine[J]. Acta Energiae Solaris Sinica, 2020, 41(3): 192-198.
[8] 李琪飞, 李光贤, 权辉, 等. 水泵水轮机在泵工况的导叶水力矩特性[J]. 工程热物理学报, 2018, 39(10): 2 193-2 199.
LI Qifei, LI Guangxian, QUAN Hui, et al. Hydraulic torque characteristics of guide vane at pump mode in a pump turbine[J]. Journal of Engineering Thermophysics, 2018, 39(10): 2 193-2 199.
[9] 孙壮壮, 张友明, 夏鹤鹏, 等. 不同工况下轴流泵转子径向力及其压力脉动分析[J]. 灌溉排水学报, 2019, 38(1): 122-128.
SUN Zhuangzhuang, ZHANG Youming, XIA Hepeng, et al. Analysis of rotor radial force and pressure fluctuation of axial flow pump water different flow conditions[J]. Journal of Irrigation and Drainage, 2019, 38(1): 122-128.
[10] 杨帆, 刘超, 许旭东, 等. S形贯流泵装置水力模型非定常水动力特性分析[J]. 应用基础与工程科学学报, 2016, 24(3): 442-453.
YANG Fan, LIU Chao, XU Xudong, et al. Unsteady hydrodynamic performance of hydraulic model in S-shaped shaft extension tubular pumping system[J]. Journal of Basic Science and Engineering, 2016, 24(3): 442-453.
[11] 江伟, 李国君, 张新盛, 等. 离心泵蜗壳进口边对叶轮径向力影响的数值模拟[J]. 水利学报, 2014, 45(2): 248-252.
JIANG Wei, LI Guojun, ZHANG Xinsheng, et al. Numerical simulation of radial force on impeller in a centrifugal pump with different volute inlet edges[J]. Journal of Hydraulic Engineering, 2014, 45(2): 248-252.
[12] 肖若富, 吕腾飞, 王福军. 双蜗壳式双吸泵隔板结构对叶轮径向力的影响[J]. 农业机械学报, 2011, 42(9): 85-88.
XIAO Ruofu, LYU Tengfei, WANG Fujun. Influence of rib structure in double-volute centrifugal pumps on the impeller radial force[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(9): 85-88.
[13] 李琪飞, 张正杰, 李仁年, 等. 水泵水轮机泵工况空化特性与转轮受力分析[J]. 农业机械学报, 2018, 49(1): 137-142.
LI Qifei, ZHANG Zhengjie, LI Rennian, et al. Analysis of cavitation performance and force on runner of pump-turbine in pump mode[J]. Transactions of the Chinese Society for Agricultural Machinery, 2018, 49(1): 137-142.
[14] 商邑楠, 罗灿, 夏臣智, 等. 竖井贯流泵进水流道的数值模拟研究[J]. 江西水利科技, 2019, 45(4): 241-246.
SHANG Yinan, LUO Can, XIA Chenzhi, et al. Numerical simulation of shaft tubular pump inlet duct[J]. Jiangxi Hydraulic Science & Technology, 2019, 45(4): 241-246.
[15] 杨帆, 刘超, 汤方平, 等. 竖井贯流泵装置内部流动数值模拟与性能分析[J]. 水力发电学报, 2014, 33(1): 178-184.
YANG Fan, LIU Chao, TANG Fangping, et al. Numerical simulation of 3D internal flow and performance analysis of the shaft tubular pump system[J]. Journal of Hydroelectric Engineering, 2014, 33(1): 178-184.
[16] 阎超, 于剑, 徐晶磊, 等. CFD模拟方法的发展成就与展望[J]. 力学进展, 2011, 41(5): 562-589.
YAN Chao, YU Jian, XU Jinglei, et al. On the achievements and prospects for the methods of computational fluid dynamics[J]. Advances in Mechanics, 2011, 41(5): 562-589.
[17] DEVALS C, VU T C, GUIBAULT F. CFD analysis for aligned and misaligned guide vane torque prediction and validation with experimental data[J]. International Journal of Fluid Machinery and Systems, 2015, 8(3): 132-141.
The Influence of Guide Vanes on Force Imposed to Bidirectional Shaft Tubular Pump
LIN Pengcheng1,BAI Zhou2, TANG Fangping1*, ZHANG Yedong3, ZHENG Bin3, WANG Yong4
(1. School of Hydraulic Energy and Power Engineering, Yangzhou University, Yangzhou 225000, China; 2. Shuyang Water Conservancy Bureau of Jiangsu Province, Suqian 223600, China; 3. Qiantang Basin Center of Zhejiang Province, Hangzhou 310020, China;4. Zhejiang Water Conservancy and Hydropower Construction Holding Development Company, Hangzhou 310020, China)
【Objective】Bidirectional shaft tubular pump is a device commonly used in hydraulic projects. The aim of this paper is to study the impact of guide vane numbers on the force imposed to the pump when it is under different working conditions.【Method】The investigation was based on computational fluid dynamics (CFD) and experiments conducted in a real engineering project. Water flow in the pump was turbulent and described by the RNGturbulence model. The experimental data was used to calibrate the model, and the validated model was then used to analyze the impact of guide vane numbers on the pump under different working conditions.【Result】Under back and forth operation condition, the average axial force imposed to the pump by different guide vane numbers was comparable. Making the ratio of guide vane numbers to blade numbers an integer increased the peak axial force pulsation significantly, risking pump operation. The radial force imposed to the impeller was minimal and can be neglected in design. It was also found that setting the number of guide vanes even can reduce the radial force imposed to the pump by the guide vane.【Conclusion】The number of guide vanes and the number of blades combined to affect the force imposed to the pump. Our results indicated that design should avoid the ratio of the guide vane numbers to the blade numbers being an integer.
guide vane number; force analysis; Two-way shaft tubular pump device; numerical simulation; model test
1672 - 3317(2023)03 - 0082 - 08
TH312
A
10.13522/j.cnki.ggps.2021445
林鹏程, 柏周, 汤方平, 等. 不同导叶张数对双向竖井贯流泵装置影响的受力分析[J]. 灌溉排水学报, 2023, 42(3): 82-89.
LIN Pengcheng, BAI Zhou, TANG Fangping, et al. The Influence of Guide Vanes on Force Imposed to Bidirectional Shaft Tubular Pump[J]. Journal of Irrigation and Drainage, 2023, 42(3): 82-89.
2022-08-03
国家自然科学基金项目(51376155);江苏省自然科学项目(BK20190914);江苏省高校自然科学研究项目(19KJB570002);扬州市自然科学项目(YZ2018103);江苏省水利科技项目(2017031);江苏省高校优势学科建设项目(PAPD)
林鹏程(1998-),男。硕士研究生,主要从事轴流泵研究。E-mail: 649315792@qq.com
汤方平(1964-),男。教授,主要从事轴流泵研究。E-mail: tangfp@yzu.edu.cn
责任编辑:赵宇龙
