单侧大帆板卫星对日姿态轨迹优化及跟踪控制
2023-04-19于铭晗贾英宏
于铭晗,贾英宏
北京航空航天大学, 北京 100191
0 引 言
近年来,由于各类商业需求,近地小卫星得到广泛关注.此类卫星平台较小,且由于发射空间和有效载荷的限制,卫星有时仅单侧带有尺寸较大的太阳帆板,在轨飞行过程中长时间保持对日巡航以满足星载能源需求.SpaceX的“星链”卫星即是一个典型的例子[1].由于近地轨道特性和单侧太阳帆板构型的影响,在轨飞行时卫星受到的气动力矩和引力梯度力矩相对较大,容易引起较大的三轴角动量积累.而受限于较小的卫星平台,用于姿控的角动量交换装置的角动量吸收能力有限.因此,对于此类卫星,空间环境干扰力矩引起的三轴角动量积累是需要考虑的问题.
常见的对日巡航基准坐标系是太阳黄道对日基准坐标系[2],该坐标系的定义如下:以日地连线方向作为Z轴,以黄道平面的法向方向为Y轴,X轴的方向由右手法则确定.由于太阳位置在短时间内可以视为常值,因此太阳黄道对日基准坐标系的运动规律比较简单.由于对日巡航只要求卫星太阳帆板的法线方向指向太阳,此时卫星的姿态并不是固定的,卫星可以绕该法线方向进行旋转.在轨道的任意位置,卫星能保持对日巡航模式的姿态都有无数种.如何找到一条期望的姿态轨迹,在保持对日巡航的基础上,使卫星运行一个周期三轴角动量积累最小是问题的关键.
对日巡航的效果与太阳帆板的自由度有关,自由度越大,太阳帆板的指向限制就越少,对日巡航的效果也就越好,但每增加一个自由度,就会降低整个卫星的稳定性.文献[3]对一种低轨道的对地观测卫星固定太阳帆板的最佳的对日指向问题进行了研究,最终得到了解析表达和最优结果.该文献以某一段时间的平均功率最小为优化目标,建立了固定太阳帆板指向和轨道高度,太阳方向和轨道平面夹角的函数,最终得到了上述几个参数变化时,固定太阳帆板的最优指向.LANDIS[4]研究了一种低轨道太空站的单自由度太阳帆板的对日定向问题,主要考虑了帆板指向带来的气动干扰问题并提出了一种对日定向的方案,对低轨道航天器具有很大的参考意义.而对于双自由度太阳帆板卫星,HABLANI[5]提出了简单模型的双自由度太阳帆板对日定向的方案,并设计了对应的跟踪规律.由于双自由度太阳帆板可活动范围较大,卫星在轨运行期间经常会遇到遮挡问题,文献[6]针对上述方案,综合考虑了双自由度太阳帆板大范围转动带来的遮挡问题,提出了一种改进方案.
目前,关于卫星对日巡航控制问题已有大量相关研究.李庆军等[7]提出了一种能跟踪太阳运动的准对日定向姿态方案.首先给出了准对日定向姿态数值的构造方法,然后设计了PD控制律,使太阳能阵列在任意姿态初始条件下收敛到准对日定向姿态;谭永光[8]研究了变参数模型的太阳帆板卫星的姿态稳定和驱动机构驱动帆板对日定向的控制问题,提出了一种滑模变结构控制,提高了卫星姿态控制的精度和稳定度;朱军年[9]研究了太阳同步轨道卫星太阳帆板的对日定向控制,针对单翼、单自由度、匀速驱动的太阳同步轨道卫星帆板的对日定向控制问题,分别研究了轨道偏心率、地球非球形摄动、日月引力、大气阻力、太阳光压等因素对卫星帆板对日定向精度的影响作用规律;季浩然等[10]提出一种平稳的以对地指向偏差为约束的对日定向方法,此方法能够大幅度降低卫星期望角速度的峰值和能耗,同时又能够满足对日指向和对地指向的需求.但上述文献在对日巡航的研究中均未考虑角动量积累的问题.
本文针对单侧大帆板卫星长时间在轨运行期间的角动量积累问题,利用GPOPS-Ⅱ[11]得到期望的对日姿态轨迹,并设计了控制器对该姿态轨迹进行跟踪控制.建立了单侧大帆板卫星的姿态动力学模型;根据建立的卫星模型优化得到期望的对日姿态轨迹;考虑惯量矩阵不确定和未知干扰力矩的影响,设计了自适应滑模姿态跟踪控制律,通过自适应律调节控制增益,无需已知系统不确定性上界;通过仿真验证了所得姿态轨迹的正确性以及控制器的有效性.
1 单侧大帆板卫星的建模
本文研究的单侧大帆板卫星的结构示意图如图1所示.文中主要针对帆板与星体固定安装,无驱动机构的情况下进行研究.由于卫星为非对称结构,质心不在卫星星体上,先根据卫星尺寸及质量分布计算质心坐标,以质心为坐标原点建立本体坐标系,进而计算出惯量矩阵,在此基础上对卫星进行动力学和运动学建模.
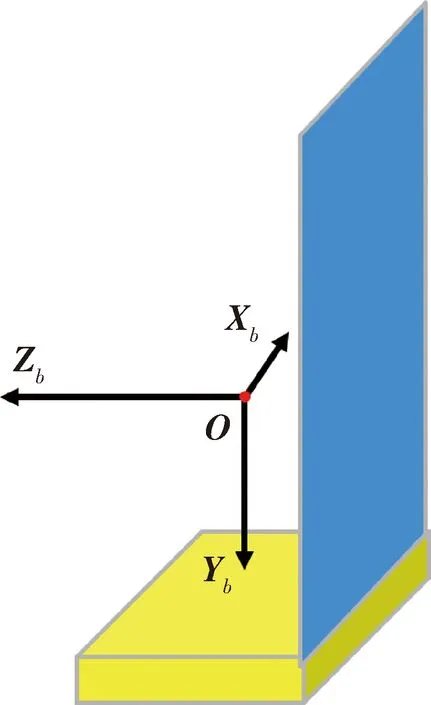
图1 单侧大帆板卫星结构示意图Fig.1 Schematic diagram of the satellite with single-sided solar panel
为了避免欧拉角奇异问题,采用四元数来描述卫星姿态.卫星本体系相对于惯性系的四元数记为
Q=[q0q]T
(1)
式中,q=[q1q2q3]T为矢部,q0为标部.
卫星本体系相对于惯性系的三轴角速度记为
ω=[ωxωyωz]T
(2)
则姿态运动学方程可以写为
(3)
式中,右上标“×”表示列阵的叉乘反对称阵.
不考虑帆板振动,则卫星的姿态动力学方程为
(4)
式中,I为卫星的惯量矩阵,Cw为飞轮组的安装矩阵,hw为角动量交换装置的角动量向量,Tc为角动量交换装置输出的控制力矩,Tg为引力梯度力矩,Ta为气动力矩,Td为其它未知干扰力矩.
卫星受到的引力梯度力矩可表示为
Tg=3n2R×IR
(5)
式中,n为轨道角速率,R为地心到航天器质心的矢径的单位方向向量.
在气动力建模方面,气动力及气动力矩计算公式[12]
(6)
式中,Cd为气动系数,ρ为大气密度,Ap为有效迎流面积,V为来流速度大小,V为来流方向的单位矢量,Cp为质心压心距,文中取卫星每个面的形心为该面的压心,而卫星的质心在建立本体坐标系时已给出.
气动力的求解关键在于大气密度和有效迎流面积的计算.本文中大气密度的计算采用SA76大气模型[13].考虑到该单侧大帆板卫星形状比较规则,各个面之间遮挡关系容易判断,因此没有用常见的“微元法”,而采用“直接法”.
2 对日巡航模式下的姿态轨迹优化
如图2所示,对日巡航模式的任务是使卫星本体系-z轴指向太阳方向,以满足星载能源的需求.
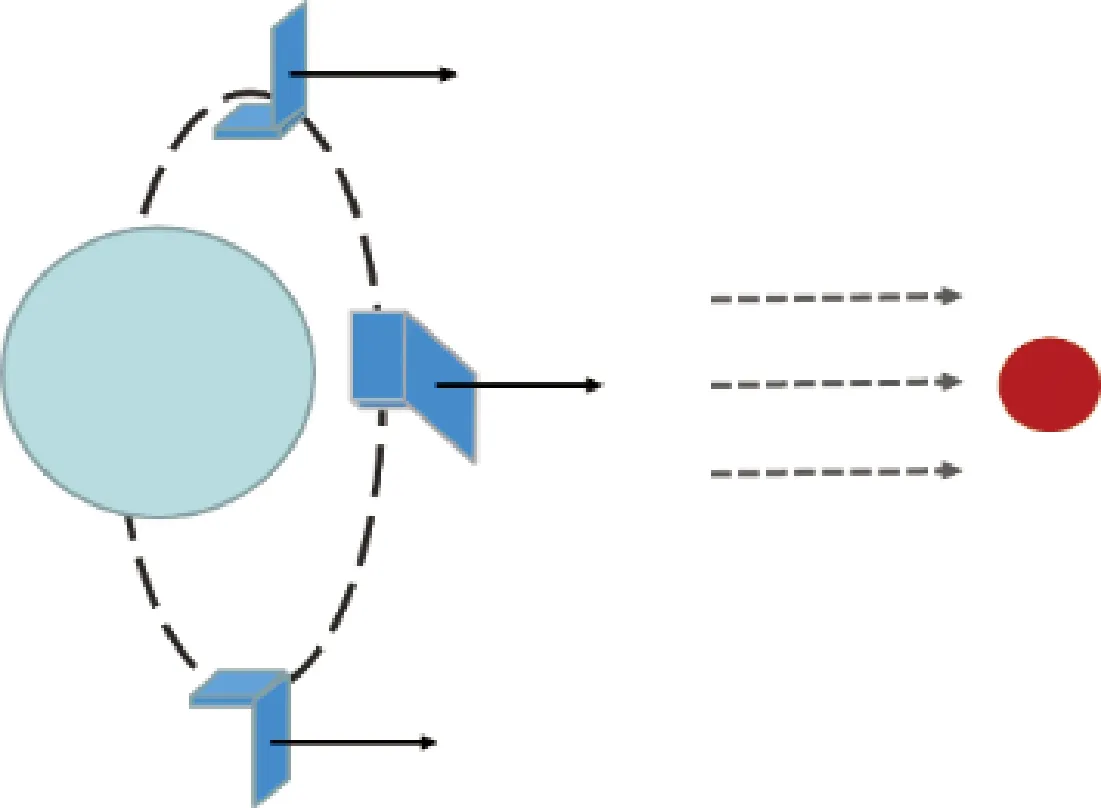
图2 对日巡航模式示意图Fig.2 Schematic diagram of sun-pointing mode
对日巡航是一个长期的在轨工作状态,由于环境力矩的存在,会产生角动量的积累.而大部分卫星对日巡航模式只需要保证一个轴对准太阳,对其他2个轴的指向没有要求.本文的目的是要得到使卫星三轴角动量积累最少的姿态轨迹,因此需要在对日的基础上对姿态轨迹进行优化.
本文采取的优化方法是高斯伪谱法[14].利用以高斯伪谱法为原理的第2代通用最优控制问题求解软件GPOPS-Ⅱ进行求解,该软件是用于解决非线性最优控制问题的通用MATLAB软件包[15],由美国佛罗里达大学的RAO等人编写完成[16-17].利用该工具包,能解决上述单轴指向确定条件下角动量积累最小的姿态轨迹轨划问题.
根据优化模型的要求,对上述姿态轨迹优化问题进行描述.首先将以状态方程的形式描述单侧大帆板卫星的姿态动力学方程表示如下:
(7)
(8)
u=Tc
(9)
式(8)中,F(ω)为姿态运动学相关表达式,由式(3)获得.优化时把控制力矩Tc视作状态量,以保证一个轨道周期的初始和终止的角加速度一致,进而保证一个周期的初末状态一致,详细的初末状态约束条件将在下文给出.鉴于所研究的卫星受到的气动力矩和引力梯度力矩占干扰力矩主导地位,其他干扰力矩Td一般较小且未知,因此在优化中未予考虑.
优化指标定义为一个周期内干扰力矩积累的角动量积累最小,这里主要考虑气动力矩和重力梯度力矩的影响,优化指标表示为
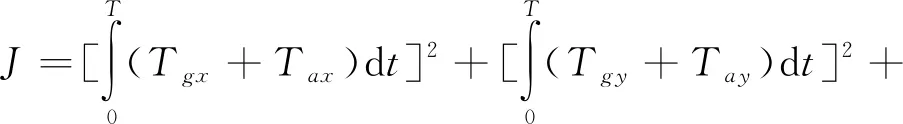
(10)
式中,T为轨道周期.
对于路径约束,该优化问题的路径约束为对日约束,即卫星本体系-z轴指向太阳,具体表示为
(11)

对状态变量的约束要满足以下条件
(12)
式中,qimin、qimax、ωimin、ωimax、uimin和uimax在系统描述函数中合理取值.
如前所述,本文研究的是一个周期的卫星姿态轨迹规划问题,需保证卫星初末状态的一致,因此对于卫星在轨运行的初末状态也存在约束
(13)
式中,qi0、ωi0和ui0分别为初始状态的四元数、角速度和控制力矩分量,qif、ωif和uif分别为终止状态的四元数、角速度和控制力矩分量.
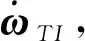
3 控制律设计
尽管姿态优化中也可得到优化控制量,但其中并未考虑各种模型不确定性.实际控制中,仍需设计反馈控制律,以实现优化的姿态轨迹.在姿态控制律设计过程中,本文主要考虑的不确定因素为惯量参数不确定和未知外干扰力矩.
首先定义如下的误差姿态四元数和误差角速度
(14)

式(14)所定义的误差四元数和误差角速度符合如下的运动学关系:
(15)
容易证明,当误差四元数的矢部qe=0时,卫星本体坐标系与期望坐标系指向一致,因此将qe作为姿态跟踪误差.控制器设计目的即是要使姿态跟踪误差qe和角速度跟踪误差ωe均收敛于零.
考虑到惯量矩阵的不确定性,令I=I0+ΔI,I0为惯量矩阵的标称值,ΔI为惯量矩阵的不确定部分,这里假定ΔI相对于I0很小.由于惯量不确定,姿态轨迹优化仅能基于标称惯量进行;但由于惯量不确定部分相比标称值一般为小量,因此姿态轨迹优化仍具有重要意义.由式(14)中误差角速度的定义以及惯量不确定描述,姿态动力学方程式(4)可写为如下误差动力学方程的形式:
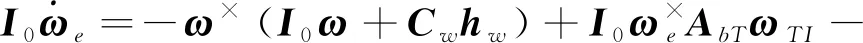
(16)
式中,Tg0为以标称惯量计算的引力梯度力矩,d为系统的聚合扰动[18],可表示为

(17)

(18)
由以上描述可见,系统惯量参数不确定和未知外干扰使得系统具有上界难以确定的聚合扰动,这要求所设计的姿态跟踪控制律具有较好的鲁棒性,因而本文采用鲁棒性较好的滑模控制方法;同时由于聚合扰动上界不易获得,本文在滑模控制的基础上设计自适应律以保证系统的稳定性.
选取滑模面
s=ωe+Kqe
(19)
式中,s=[s1s2s3]T∈R3,K∈R3×3为正定对角矩阵.由四元数运动学关系可知,当s→0时,有qe→0和ωe→0.
基于上述滑模面,设计姿态跟踪控制律如下:
Tc=ueq+uN+uh
(20)


(21)
设计uN为
(22)
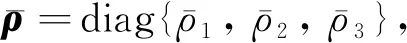
(23)

该文采用的数据资料主要包括2017年1m分辨率正射遥感影像(DOM)、荣成市第二次全国土地调查数据、生态红线划定资料、永久基本农田数据、土地坡度等级数据、耕地利用质量等级数据、耕地后备资源数据、水资源、地质灾害分布图等。所用数据大部分为矢量数据,其余图件资料经矢量化后作为后续数据统计分析的基础资料。利用遥感影像,将荣成市第二次全国土地调查数据更新至影像获取时相,提高数据的现势性。
(24)
式中,qi0、qi1和qi2为正的控制参数.
最后,设计uh为
uh=-KDs
(25)
式中,KD∈R3×3为对角矩阵.
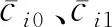
记uN=[uN1uN2uN3]T,将uNi改进为
(26)
式中,ξi是比较小的正数.
自适应参数估计率(24)改进为
(27)
式中,ψi0、ψi1和ψi2是较小的正实数.
下面给出系统的稳定性证明.
证明:选取正定无界的Lyapunov函数为
(28)

Lyapunov函数的时间导数为
(29)

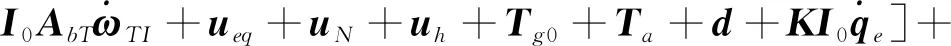

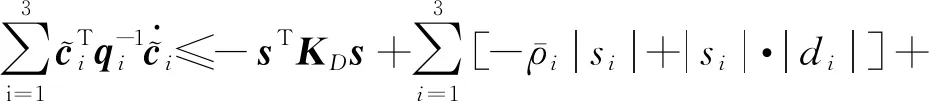

(30)
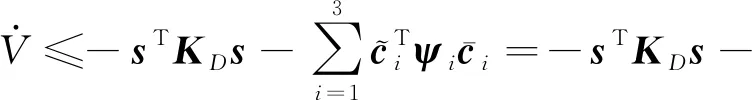
(31)
式中,ψi=diag{ψi0,ψi1,ψi2}.


(32)
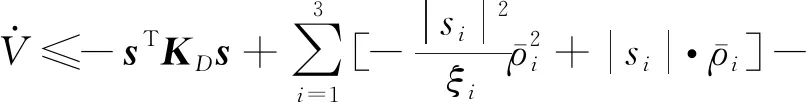
(33)

(34)
注意到ci、ξi和ψi均为常值,因此由式(31)、式(34)及文献[22]的结论可知,系统是最终一致有界稳定的.
4 数值仿真与结果分析
本文以“星链”卫星为背景,研究一种单侧大帆板卫星,该卫星的本体尺寸为2.8 m×1.4 m×0.2 m,太阳帆板尺寸为2.8 m×10 m,卫星的总质量为229 kg.另外,计算得到仿真时刻太阳在惯性系的位置为[0.223 4 -0.894 2 -0.387 7]T,卫星的轨道相关参数如表1所示,后面优化以及姿态控制仿真,均采用该卫星参数.
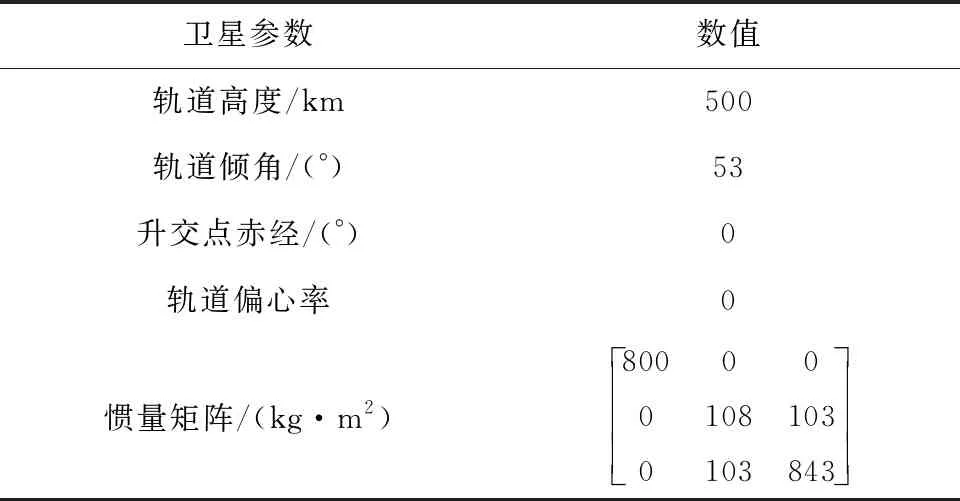
表1 卫星轨道相关初始参数Tab.1 Initial parameters of the satellite orbit
4.1 姿态轨迹优化仿真结果
针对该姿态轨迹优化问题,以角动量积累最小为优化指标,以对日定向为约束,利用MATLAB中高斯伪谱法相关软件包GPOPS-Ⅱ进行求解,基于MATLAB R2019b平台进行仿真,仿真时长为卫星在轨运行的一个周期,卫星轨道相关信息如上所示.得到优化后的姿态轨迹如图3~4所示.
从图3~4可以看到,优化得到的对日姿态轨迹能满足卫星在轨运行一个周期的初末状态一致.从图4可以看到,仅卫星本体系的z轴有角速度,而其他两轴的角速度大致为零,这也符合对日姿态轨迹优化的过程.实际上,当卫星本体系-z轴指向太阳后,要得到期望的对日姿态轨迹,仅需卫星绕本体系z轴旋转,仅在z轴上有角速度.因此,得到的对日姿态轨迹符合实际的物理意义.而能否满足在轨运行一个周期后干扰力矩积累的角动量最小,需要进一步对其进行姿态跟踪并对比验证.

图3 优化的姿态四元数Fig.3 The optimized attitude quaternion

图4 优化的角速度Fig.4 The optimized angular velocity
4.2 姿态跟踪控制仿真结果
仿真中卫星的轨道初始参数同上,仿真中卫星的初始状态参数如表2所示.

表2 卫星初始状态Tab.2 The initial state of the satellite
干扰力矩取为
为充分验证所设计的控制律的有效性和优越性,在姿态跟踪仿真中,将本文设计的自适应滑模控制律和常用的PID控制律仿真结果进行对比.由卫星误差动力学和运动学模型,PID控制律的设计如下:

(35)
PID控制器的参数如表3所示.

表3 PID控制器参数Tab.3 Parameters of the PID controller
本文所设计的自适应滑模控制律控参数如表4所示.

表4 自适应滑模控制器参数Tab.4 Parameters of the adaptive sliding mode controller
姿态跟踪控制仿真时长为卫星的一个轨道周期.图5~6分别给出了PID控制律和自适应滑模控制律得到的姿态跟踪误差.图7~8分别给出了PID控制律和自适应滑模控制律得到的角速度跟踪误差.图9~10分别给出了PID控制律和自适应滑模控制律得到的卫星三轴力矩.
在自适应滑模控制律的作用下,姿态跟踪误差能够在200 s内收敛在10-5量级,误差角速度也能在200 s内收敛到10-4(°)/s量级,姿态跟踪控制精度较高.图6中之所以存在静差,是因为设计控制律时,为了避免颤振,将非连续控制力矩改进为连续的控制力矩(平滑处理),此时系统不具有渐近稳定性,是一致有界稳定的,所以会有静差存在.与PID控制进行对比,当存在未知干扰和惯量不确定影响时,特别是随着干扰增大,本文设计的控制律控制精度要更高一些,而且调参过程更加简单.

图5卫星姿态跟踪误差(PID控制)Fig.5 Attitude tracking error of the satellite (PID control)

图6 卫星姿态跟踪误差(自适应滑模控制)Fig.6 Attitude tracking error of the satellite (adaptive sliding mode control)
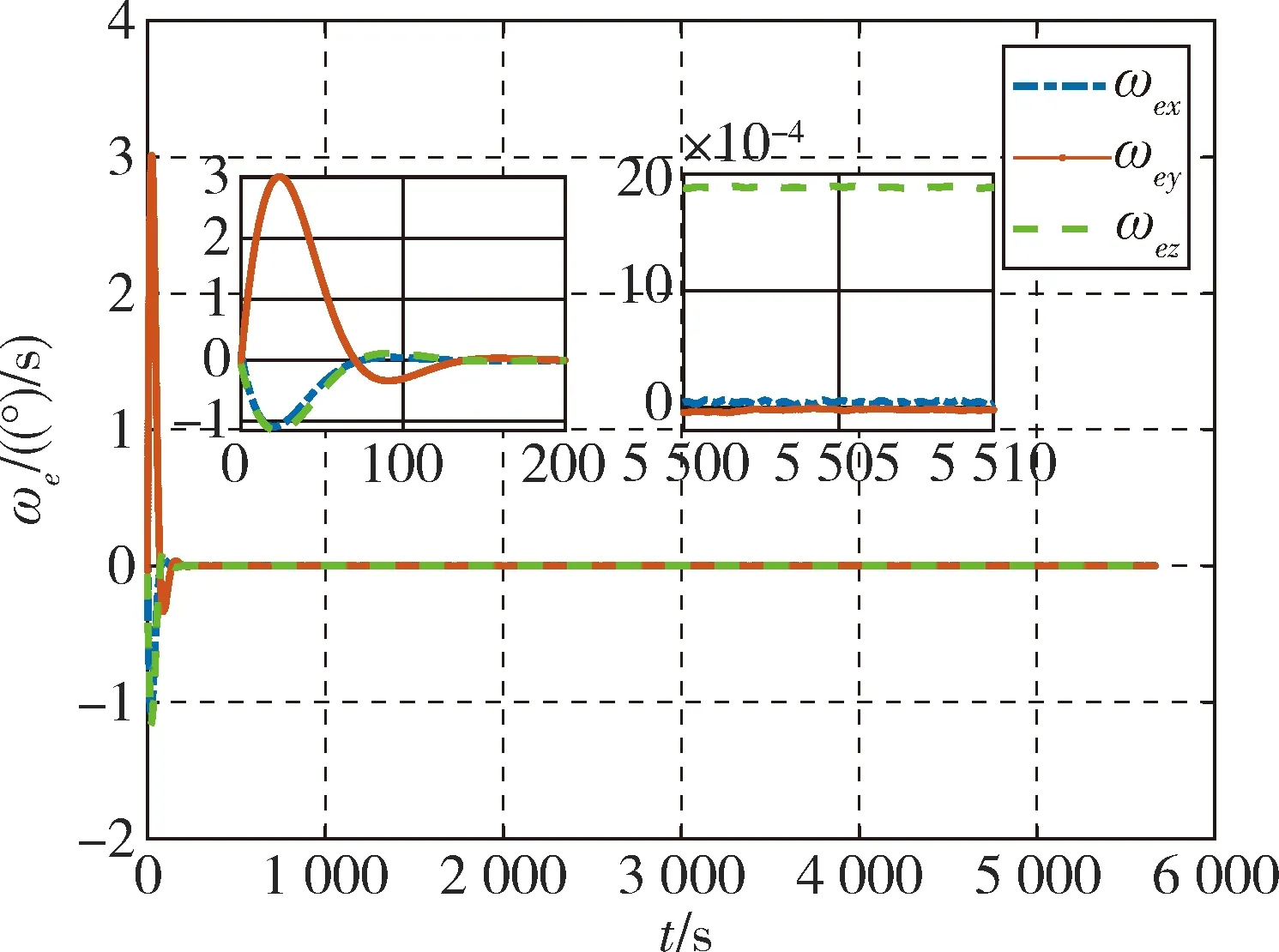
图7 卫星角速度跟踪误差(PID控制)Fig.7 Angular velocity tracking error of the satellite (PID control)
图11是卫星本体系-z轴与太阳方向的夹角,最终也收敛到零附近,验证了对日巡航姿态的正确性.为验证姿态优化对减小三轴角动量积累的有效性,仿真中将本文所研究的优化后的姿态轨迹与未优化的太阳黄道对日基准坐标系在相同的控制律下进行比较,仿真得到的优化前后角动量积累的平方如图12所示.可见姿态轨迹优化后,卫星三轴角动量的积累得到了大幅降低,优化效果显著.

图9 卫星三轴控制力矩(PID控制)Fig.9 Three-axis control torque the of satellite (PID control)

图10 卫星三轴控制力矩(自适应滑模控制)Fig.10 Three-axis control torque the of satellite (adaptive sliding mode control)
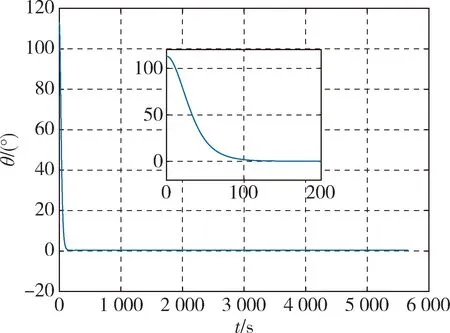
图11 本体系-z轴与太阳方向夹角Fig.11 The angle between the -zaxis of the body coordinate system and the direction of the sun

图12 优化前后卫星三轴角动量的平方对比Fig.12 Comparison of the square of the three-axis angular momentum of the satellite before and after optimization
5 结 论
本文建立了单侧大帆板卫星的动力学模型,并在该模型的基础上,利用以高斯伪谱法为原理的MATLAB工具包GPOPS-Ⅱ进行对日姿态轨迹优化,得到了一个周期内使卫星三轴角动量积累最小的对日姿态轨迹.在所得到的卫星姿态轨迹的基础上进行了姿态跟踪控制器的设计,并与PID控制器对比,所设计的自适应滑模控制器在卫星具有惯量不确定和未知外干扰的情况下是最终一直有界稳定的,且控制器设计无需已知系统不确定性上界.数值仿真结果表明,所设计的姿态跟踪控制器可以准确跟踪优化姿态轨迹;相比常用的太阳黄道对日基准坐标系,优化后的姿态轨迹可以显著降低卫星三轴角动量积累.
