远距离逆行轨道上的近距离自然及受控编队
2023-04-19杨驰航符弘岚张皓
杨驰航,符弘岚,张皓
1.中国科学院 空间应用工程与技术中心 太空应用重点实验室,北京 100094
2.中国科学院大学,北京 100049
通过多个航天器之间的协同合作,编队飞行技术可以完成很多单个航天器难以完成的任务。特别是近距离编队飞行,已经深入应用至多种航天任务场景,包括交会对接、伴飞卫星、近距离操控等。实际上,近距离编队飞行即起源于Clohessy 和Wiltshire[1]对 航 天 器 交 会 对 接 的 研究,它为交会对接过程提供了相对运动动力学基础,而交会对接是实现空间站搭建与维持、载人登月等大型空间任务的基础技术之一[2]。对于这些大型空间任务,常常设计伴飞卫星用于舱外观测、空间科学研究等,中国空间站的伴飞巡天空间望远镜是其中的典型代表[3]。另外,随着在轨补给与维修技术的发展,近距离操控也逐渐成为编队飞行技术的重要应用场景,2019年,ViviSat公司成功发射了MEV-1,用于在轨卫星的位置校正,以延长卫星寿命[4]。
受限于航天事业的发展,目前近距离航天器编队的研究主要集中于地球轨道[5-6]。而由于地球轨道较为拥挤的轨道资源以及一些天然的动力学限制,地月空间的重要性逐渐凸显。作为深空与近地空间的交界区域,地月空间轨道具有独特的位置优势。远距离逆行轨道(Distant Retrograde Orbit,DRO)是地月空间中一族大尺度、绕月逆行的周期轨道[7],具有良好的轨道稳定性,不需要频繁的位置保持。距离地球及月球距离适中,便于实现去地球轨道及月球轨道的转移,适用于深空空间站[8]、小行星预警与防护[9]等长期空间任务。因此有必要研究DRO 上的近距离编队飞行,以为DRO 主任务提供必要的辅助。
目前,地月空间的近距离编队研究主要集中于Halo 轨道。Halo 轨道由于其不稳定性,其上的研究多偏重控制设计。大多数研究采用连续控制的方式使Halo 轨道上的近距离相对运动保持稳定,或维持期望的构型,常用的控制方法包括哈密尔顿结构保持控制[10-11]、线性反馈控制[12-13]、非线性最优控制[14-15]等。也有学者采用脉冲控制维持Halo 轨道上的近距离编队[16-17]。除此之外,为设计自然编队或减小控制燃耗,有少数学者研究了Halo 轨道附近的近距离自然相对运动动力学。 Gómez[18]和Héritier[19]等分析了Halo轨道附近的动力学结构,得到了发散速度较慢、适宜于设计编队的区域。Howell 和Marchand[20]基 于Floquet 理 论 给出了Halo 轨道线性化相对运动模型的不同模态,Simanjuntak[21]和周敬[22]等对每个模态做了进一步的具体分析,并据此给出了线性化相对运动模型的半解析解。
相比于Halo 轨道,DRO 上的近距离相对运动的研究非常少,目前仅有少数学者做了相对运动模型相关的研究。Franzini 和Innocenti[23]相 对于三体动力学中的周期轨道建立了通用的线性化相对运动模型,可用于DRO 上的近距离相对运动研究。 另 外,Conte 和Spencer[24],以 及Ueda[25]等简单分析了DRO 上的线性化相对运动模型的误差。
不同于Halo 轨道,DRO 轨道不仅支持近距离受控编队,还支持近距离自然编队。因此,本文对DRO 上的自然与受控2 种编队一起,做了较为详细的分析与设计。为设计编队,首先基于Floquet 理论得到了DRO 附近线性化相对运动模型的通解,并对解做了分类与分析。并以相对运动通解中的周期解为基础,设计了自然伴飞编队。为打破自然编队的动力学限制,引入了脉冲控制,设计了圆形绕飞受控编队,并分析了不同参考轨迹对应的燃耗,另外还针对两点之间的转移问题设计了参考轨迹,实现了两点之间的安全转移。
1 圆型限制性三体问题与DRO
圆型限制性三体问题是研究地月空间轨道的常用模型。在圆型限制性三体问题中,假设地球与月球绕二者的共同质心沿圆轨道相互旋转。为研究一个相比于地球及月球质量可忽略的卫星在二者引力场中的运动,建立以月球质心为原点的旋转坐标系M:X轴由地心指向月心;Z轴沿月球相对于地球的角动量方向;Y轴与前两者构成右手直角坐标系,如图1 所示。月心惯性系I的3 个坐标轴X'、Y'及Z'的定义与月心旋转坐标系M类似,但其依据的并非实时的地月位置,而是某个固定时刻的地月位置。

图1 月心旋转坐标系Fig.1 Moon-centered rotating coordinate system
为方便起见,采用无量纲的归一化单位进行分析,归一化的质量、位置与时间单位分别为
式中:REM为地月距离;G为引力常数;mE及mM分别为地球及月球的质量。
在月心旋转坐标系中,卫星运动的动力学模型为[23]
式中:X、Y、Z分别为卫星的位置;RE及RM分别为卫星至地球与月球的距离;μ为
DRO 为圆型限制性三体问题中的一类平面周期轨道,其绕月逆行,轨道稳定,适用于地月空间长期任务。通过庞加莱界面选取初值,再采用打靶算法优化迭代[26],可得到平面DRO。
定义在坐标系M中DRO 附近的一个微小扰动从0 时刻至t时刻的状态转移矩阵为ΦM(t),则其从0 时刻至一个周期之后的状态转移矩阵ΦM(T)为单值矩阵。单值矩阵的特征值可以彰显出周期轨道的稳定性。通常,采用如式(4)所示的稳定性指数来表征DRO 的稳定性[26]:
式中:λi表示ΦM(T)的第i个特征值,且若所有特征值对应的稳定性指数均等于1,则周期轨道是线性稳定的;当存在模大于1 的稳定性指数时,周期轨道是不稳定的,且模越大,周期轨道不稳定性越强。
不同周期的DRO 对应的稳定性指数s如图2所示。可以看到,除周期非常大的少部分DRO的稳定性指数略大于1 之外,其余DRO 均是稳定的。

图2 DRO 稳定性指数Fig.2 Stability indexes of DRO
在众多的DRO 中,周期位于10~20 d 左右的DRO 距离地球和月球均距离适中,稳定性强,可工程化应用。这里以周期为日月会合周期(29.5 d)一半,也即14.75 d 的DRO 为例,其轨道如图3 所示。

图3 2∶1 DROFig.3 2∶1 DRO
图3(b)中,月球位于坐标原点,可见DRO 是一种大尺度的月球周期轨道。由于该DRO 的周期为14.75 d,与月球公转周期(27.28 d)不共振,因此其在地月质心惯性坐标系中存在进动,不是闭合的周期轨道。
2 线性化相对运动动力学及其解
2.1 相对运动动力学
考虑DRO 上2 个卫星,其中主星(Chief satellite)位于一条DRO 周期轨道上,副星(Deputy satellite)位于主星附近。为研究DRO上的相对运动,定义以主星为质心的LVLH(Local-Vertical-Local-Horizontal)相对运动坐标系L:x轴由月球指向主星;z轴沿主星相对于月球的角动量方向;y与前两者构成右手直角坐标系。
在坐标系L中,线性化的相对运动动力学方程为[23]
式中:x=[rTvT]T=xrel=xd-xc为副星相对于主星的相对运动状态,下标d 与c 分别表示副星与主星。且有:
式中:rc与rEM分别为主星位置矢量以及地月矢量;ΩL/I为由坐标系L至惯性系I的角速度矩阵,即
其中:ωL/I为从坐标系L相对于惯性系I的角速度;ML/I则为从坐标系L到惯性系I的矢量转换矩阵。
2.2 相对运动方程的解
由于主星轨道在月心旋转坐标系中为周期轨道,且式(5)中的系数矩阵A由主星轨道决定,因此矩阵A为周期矩阵,表示为
式中:T为主星所在DRO 的周期。
定义在坐标系L中DRO 附近从0 时刻至t时刻的状态转移矩阵为ΦL(t),则从0 时刻至一个周期之后的状态转移矩阵ΦL(T) 为单值矩阵。Floquet 理论可根据周期系数线性化方程的单值矩阵的特征值分析方程解族的情况[27],2∶1 DRO的单值矩阵的特征值包括2 对互为共轭的特征值与1 对单位特征值,当初始时刻选取为DRO 与坐标系M的X轴负向的交点时(如图3(b)所示),特征值如式(9)所示:
设:
则根据Floquet 理论,系统的一个线性无关的基础解集为[27]
其中:p1、p3、p5分别为λ1、λ3、λ5对应的特征向量;p4则为λ3对应的广义特征向量;Re 和Im 分别表示取实部和虚部算子。
在式(11)中,̂(t)(k=1,2,…,6)的周期为T,cos(α1t/T) 与sin(α1t/T) 周期为2πT/α1,cos(α5t/T) 与sin(α5t/T)周期为2πT/α5。因此x1(t)、x2(t)、x5(t)、x6(t)为相对运动拟周期解,x3(t)为周期解,而x4(t)则为发散解。当初始时刻选取为DRO 与坐标系M的X轴负向的交点时(如 图3(b)所 示),̂(0)(k=1,2,…,6)的具体值为
可以看到,̂(0)(k=1,2,3,4)对应的是地月平面内的解,而̂(0)与(0)则对应地月平面法向的解。且相对运动保持有界的充分必要条件为:初始时刻的副星相对于主星的相对运动状态r(0)为的线性组合,也即xrel(0)=-2.042 4(0)。
当初值选取为1×10-5̂(0)时,对应的基础解xk(t)在5 个周期内的轨道如图4 所示。可以看到,仿真结果与分析结果相符。2∶1 DRO 附近的相对运动解可以分为以下4 类:
1)x1(t)与x2(t)为地月平面内的拟周期运动,二者均保持有界,且会自然规避开主星,在非线性动力学上对应于附近的平面拟周期轨道。
2)x3(t)为周期解,在非线性动力学中对应于同一条DRO 上的前后编队,因此副星的相对运动轨道可以保持周期有界,如图4(c)所示。
3)x4(t) 为发散解,在动力学上对应于该DRO 附近的另一条平面DRO,由于二者周期不同,因此会存在长期漂移,如图4(d)所示,在坐标系L中主要表现为沿切向的单向漂移,以及沿径向的振幅越来越大的振动。

图4 相对运动基础解Fig.4 Fundamental solution of relative motion
4)x5(t)与x6(t)为地月平面法向的拟周期运动,在非线性动力学上对应于附近的法向拟周期轨道。
实际上,稳定的平面DRO 族均具有相似的流形结构,因此它们附近的相对运动基础解集的结构均与2:1 DRO 附近的相对运动相似。
3 近距离自然编队
对DRO 的线性化相对运动解的分析表明,其周期解x3(t)可形成一条小范围的局部伴飞轨道,因此适用于设计近距离的自然伴飞编队。因此本部分针对该周期相对运动解在做进一步分析,以设计自然伴飞编队。
在自然周期相对运动中,副星的相对运动轨迹会发生一次交叉。图5 展示了交叉点在坐标系L以及坐标系M中的位置。

图5 相对运动自然周期轨道Fig.5 Natural periodic orbit of relative motion
在一个周期内,相对运动轨迹以交叉点为界,可分为内圈与外圈2 个部分。图6 展示了不同相对运动初值下副星经过内圈与外圈轨迹所需时间,二者的比例决定了交叉点在相对运动轨迹中所处的相位。横轴y(0)表示初始时刻副星在y方向的相对运动初始值。y(0)越大,表示相对运动的尺度越大。可以看到,在近距离相对运动中,随着相对运动尺度的变化,交叉点的相位恒定不变。副星经过内圈所需的时间比外圈略长。但图5(b)显示,相对运动的外圈的轨迹更长,而内圈的轨迹更短。实际上这是由于DRO本身的形状对坐标系L的扭曲造成的,从而使得副星的相对运动速度在内圈较慢,而在外圈较快。图5(a)表明,当副星位于相对运动轨迹的外圈时,在坐标系M中,主星位于DRO 的右半圈,相比于相对运动轨迹的内圈对应的DRO 的左半圈而言,主星在DRO 的右半圈的运动轨迹更短。因此图6 的分析结果与主星的运动是一致的。

图6 副星经过内圈与外圈轨迹所需时间Fig.6 Duration time in inner and outer circles of deputy spacecraft
图7 展示了副星距离主星的最大距离与最小距离,可以看到,副星距离主星的最大距离与最小距离均随着初始相对位置的增大而增大,且与初始相对位置呈线性关系。图7 表明,只要初始时刻副星与主星存在一定的相位差,则周期相对运动轨道可以避免二者的碰撞。且二者的相对距离可以通过选择不同的相对运动初值而在线性化适用范围内适度调整。

图7 副星与主星的最小与最大距离Fig.7 Maximal and minimal distance between chief spacecraft and deputy spacecraft
为了进一步分析内圈以及外圈的特性,图8展示了内圈与外圈在x轴及y轴方向的振幅。可以看到,相对运动的内圈与外圈的运动范围随运动尺度呈线性变化。y(0)越小,则相对运动轨迹的距离主星越近,相对运动范围越小。而且相对于主星,副星具有相同的可视角度,如图9 所示。因此该编队适用于交会对接阶段的停泊。可以看到,相对运动轨迹的形状始终保持不变,这是由线性化的相对运动模型决定的。

图8 内圈与外圈振幅Fig.8 Amplitude of inner and outer circles

图9 不同初值对应的周期相对运动Fig.9 Natural periodic orbit with different scales
总体而言,DRO 上自然周期的相对运动可以使副星始终位于主星的前方或者后方的几米至几百千米的距离,沿一条周期的相对运动轨道进行运动,在无控的自然动力学作用下可以实现较为稳定的相对运动。
4 近距离受控编队
自然编队虽然可以实现低燃耗的长期伴飞,但受限于动力学,仅能实现较慢的相对运动,且其自然构型非常有限。为应对快速转移、快速绕飞等任务,需对副星施加控制。本节考虑对副星施加脉冲控制,首先对DRO 附近的近距离受控编队的燃耗与构型做了详细的分析,其次实现了两点之间的安全转移编队设计。
4.1 受控绕飞编队
为满足编队对主星进行观测的需求,需实现副星对主星的绕飞。考虑绕飞的参考轨迹为空间圆,在空间圆上选定一定数量的变轨点,在每个变轨点采用脉冲变轨可控制副星沿参考轨迹绕飞。参考空间圆的法向量、圆心与半径可以根据需求而定,示意图如图10 所示。

图10 受控绕飞示意图Fig.10 Schematic diagram of non-natural formation with circular trajectory
为分析不同的绕飞轨迹对燃耗的影响,这里具体分析了在不同变轨时间下,参考轨道法向量、圆心、尺度(半径)对燃耗的影响。在分析过程中,在每条参考轨迹上均匀选择10 个变轨点。相比于普通的绕月轨道,DRO 的周期与尺度均大1~2 个数量级,因此其上的受控编队支持更大时间跨度、以及更大尺度的绕飞。故对每条参考轨迹,我们考虑了较大的时间跨度:从0.01T至2T,也即从3.54 h 至29.5 d;且在分析参考轨道的圆心与半径时,考虑了1~100 km 尺度的绕飞。
4.1.1 参考轨道法向量对燃耗的影响
首先分析了参考轨道法向量法向对燃耗的影响。将参考轨道圆心选定为原点,也即主星所在位置;半径选为1 km。选择4 个不同的法向量方向:[0,0,1]T、[0,1,0]T、[1,0,0]T、[0,1,1]T,分别对应的于xy平面、xz平面、yz平面内的轨道,以及一条倾斜的轨道。不同法向量对应的参考轨迹的变轨燃耗如图11 所示。

图11 不同法向量对应的参考轨迹变轨燃耗Fig.11 Fuel consumption of non-natural formations with different normal vectors
当变轨时间较小时,各参考轨迹对应的总脉冲均较大,且几乎相同。随着变轨时间的增大,各参考轨迹对应的总脉冲均呈现下降趋势。这是因为当变轨时间较小时,变轨轨迹偏向于直线,故变轨脉冲较大。而当变轨时间增大时,变轨轨迹会越来越多地受到动力学的影响,从而变成越来越扭曲的曲线,如图12 所示。

图12 不同变轨时间对应的受控编队轨迹Fig.12 Trajectories of non-natural formations with different transfer time
在图11 中,整体而言,xy平面参考轨迹对应的燃耗最大,其次为倾斜轨迹,而2 条垂直于xy平面的参考轨迹对应的燃耗则相对较小。实际上,z方向的运动与xy方向的运动是相互解耦的,而二者不同的动力学特性带来了不同的燃耗。以上结果说明,在圆型限制性三体模型下,设计任务轨道时应多考虑倾斜或垂直于xy平面的轨道,有助于减少绕飞轨迹的燃耗。
4.1.2 参考轨道圆心对燃耗的影响
为分析参考轨道圆心对燃耗的影响,选定参考轨道法向量为[0,1,1]T,半径为1 km。选择3 个不同方向的圆心:[1,0,0]T、[0,1,0]T、[0,0,1]T,分别对应于x轴、y轴、及z轴方向的偏置。对每个方向的圆心偏置分别叠加0、 1、 10、100 km的大小,则可以得到不同方向、不同大小的圆心偏置对应的燃耗,如图13 所示。

图13 不同圆心偏置对应的参考轨迹的脉冲Fig.13 Fuel consumption of non-natural formations with different centers
可以看到,虽然不同方向的圆心偏置的燃耗不尽相同,但随转移时间的变化展现出相同的趋势。当圆心接近原点时,即对于没有偏置或偏置为1 km 的轨迹,每条参考轨迹对应的变轨燃耗均随时间变化呈明显的下降趋势,而且,在同样的变轨时间下,方位不同但大小相同的圆心偏置对应的变轨燃耗均相差不大。但当偏置的尺度明显大于绕飞轨迹的尺度时,也即对于图中偏置为10 km 及100 km 的轨迹,结果则完全不同。随着时间的下降,最开始燃耗呈下降趋势,但在某个时刻会出现激增。这是因为离原点越远,根据线性化近似的特性,动力学带来的加速度会越大,从而导致相对运动速度的增大,进一步使得变轨点处所需的速度脉冲增大。而另一方面,2 个变轨点之间的直线距离是相同的,因此对于离原点更远的参考轨道,副星会走过更长的路径,从而呈现出更复杂的曲线,使变轨点处前后2 段曲线的速度方向更容易出现更大的角度差,这也进一步增大了拼接速度脉冲。当变轨时间很短时,变轨曲线以直线为主,该现象并不明显,如图14(a)所示。但随着变轨时间的增大,每段的变轨轨迹受动力学的影响逐渐增多,从而显著增大了变轨点处所需要的变轨脉冲,且离原点更远的轨迹的转移轨迹明显更为复杂,如图14(b)所示。
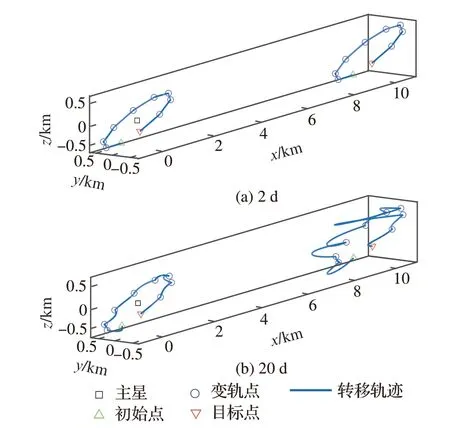
图14 不同变轨时间对应的轨迹Fig.14 Trajectories with different transfer time
因此,在做绕飞轨道设计时,应尽量将圆心放在原点附近,避免圆心有较大偏置的绕飞。该现象也从侧面增强了自然周期轨道的独特性与难以替代性。
4.1.3 参考轨道尺度对燃耗的影响
为分析参考轨迹尺度对燃耗的影响,将参考轨道法向量选定为[0,1,1]T;圆心选定为[0,0,0]T。选择3 个不同大小的半径以得到不同尺度的参考轨道:1、 10、 100 km。燃耗结果如图15所示。

图15 不同半径对应的参考轨迹的脉冲Fig.15 Fuel consumption of non-natural formations with different radii
可以看到,参考轨迹尺度越大,所需燃耗越大。如同4.1.2 节所说,离原点越远,根据线性化近似的特性,副星的速度越大,因此变轨点处所需的燃耗越大。而且,对于不同尺度的轨道,燃耗几乎呈现相同的波动形式,这是因为当圆心位于原点时,不同尺度的参考轨迹实际上彼此之间只是线性化的放缩。而包括位置与速度在内的运动状态之间同样是线性放缩,故优化得到的轨迹亦具有相同的形状,如图16 所示。

图16 不同变轨半径对应的轨迹Fig.16 Trajectories with different radii
因此,可以仅通过计算小尺度参考轨迹的燃耗来推算不同尺度参考轨迹所需的燃耗,如此可以减少燃耗分析所需的维度,从而大大减小计算量。需要注意的是对于圆心位于原点的参考轨迹,仅放大半径即可实现线性放缩;但是对于圆心不位于原点的轨迹,需同时放大参考轨迹上点的三维坐标,方能实现线性放缩。
4.2 安全转移编队
除圆轨道绕飞之外,实现副星从某个初始点至预定目标点之间的安全快速转移也是一种重要的受控轨迹应用场景。传统的安全转移编队,多采用最优控制方法、人工势场法等较为复杂的控制策略。在本节中,为考虑工程实用性,提出了一种解析方法,可直接设计出了安全转移参考轨迹,相比于传统方法结构简单、计算方便、工程实用性更强。具体的,本节将安全转移问题归结为从初始点至末端点的参考转移轨迹设计,当有了参考转移轨迹之后,在其上选取合适数量的变轨点,在变轨点处施加脉冲,从而可通过多脉冲转移沿参考轨迹抵达目标点。为了保证安全,需要使副星与主星(也即原点)之间保持足够的距离。因此这里要求参考轨迹上的所有点距离原点的距离比初始点与目标点中离原点最近的点更远。初始点与目标点的位置矢量分别用r0与rf表示,参考轨迹上的点则用矢量r1表示。
根据r0与rf是否同向共线将转移轨迹的设计分为2 种情况。首先考虑较为简单的情况,r0与rf同向共线时,也即rf=kr0,此时二者之间的夹角为0,参考轨迹可以直接设计为从初始点至末端点的直线。即
式中:p为参考轨迹上参数,决定了参考轨迹上点的位置:当p=0 时,参考轨迹位于初始点;随着p逐渐靠近1,参考轨迹逐渐逼近目标点;当p=1时,参考轨迹位于目标点。通过选定合适的p,可以在参考轨迹上选取合适的变轨点。
对于更一般化的情况,也即r0与rf并非同向共线时,则需要设计一条从初始点至末端点的曲线作为参考轨迹。依次从长度与方向2 个方面设计参考轨迹上的位置矢量r1,其长度从‖r0‖逐渐逼近‖rf‖,这里‖r‖代表矢量r的长度;方向则绕着r0与rf二者所构成平面的法向量由旋转 至,其 中表示矢量r的单位向量,该旋转可以由罗德里戈旋转公式实现。因此有:
式中:θf为与之间的夹角;pθf则为与r1之间的夹角,如图17 所示。同样的,当p=0 时,r1=r0;随 着p的不断增大,r1逐渐从r0靠近rf,直至p=1 时,r1=rf。且在整个过程中,r1的长度‖r1‖的最小值为‖r0‖与‖rf‖之间的较小值,从而可以保证在转移过程中主副星之间具有足够的安全距离。

图17 两点安全转移编队设计示意图Fig.17 Schematic diagram of trajectory design of twopoint transfer formation with safety guaranteed
为验证安全转移轨迹设计方法,这里给出一个两点转移的例子。初始点为[-3, 1, 2]Tkm,目标点为[1, 2, -2]Tkm,根据式(15)可设计出转移轨迹设计,如图18 所示。
在转移轨迹上沿式(15)中的p均匀选取4 个变轨点,总转移时间设定为2 d,各段转移时间相同,可以得到最终安全转移编队如图19 所示,耗费总脉冲为0.097 m/s。可以看到,该方法可以实现从初始点至目标点的安全转移。
进一步分析了图18 中的安全转移轨迹在不同转移时间对应的燃耗情况,如图19 所示。可以看到,其与圆构型编队具有类似的趋势,且最小脉冲0.046 m/s 出现在总转移时间为8 d 处。因此,对于任意两点之间的安全转移,可以通过分析转移时间设计出较小的脉冲,如图20 所示。另外,由线性化特点导致的放缩特性依旧存在,也即通过线性放缩可以直接得到不同尺度点之间的转移脉冲,从而可加速安全转移轨迹的设计。

图18 两点安全转移编队参考轨迹Fig.18 Reference trajectory of two-point transfer formation with safety guaranteed
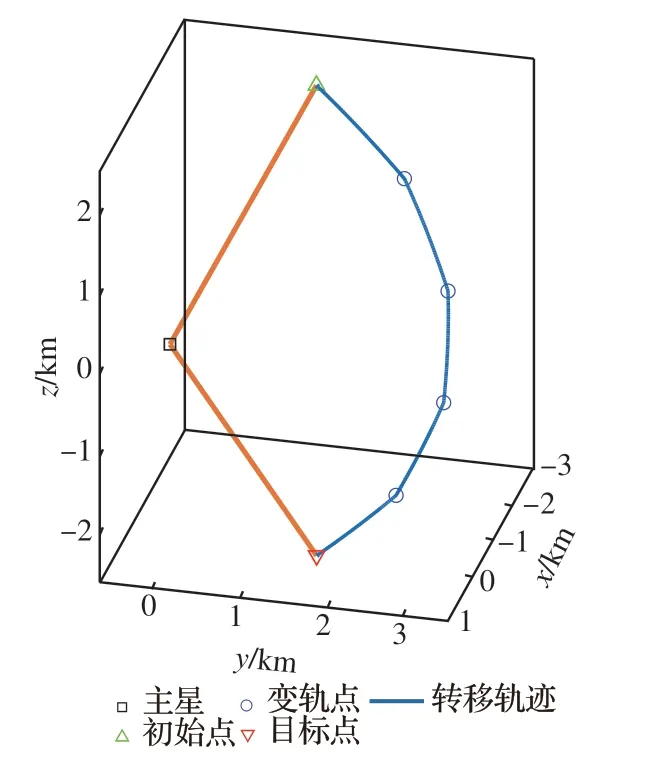
图19 两点安全转移编队转移轨迹Fig.19 Transfer trajectory of two-point transfer formation with safety guaranteed

图20 不同转移时间的两点安全转移编队脉冲Fig.20 Fuel consumption of two-point transfer formation with safety guaranteed with different transfer time
5 结 论
1)DRO 附近的近距离相对运动的通解由以下4 类解构成:地月平面内拟周期解、地月平面内周期解、地月平面内发散解以及地月平面法向拟周期解。
2)基于地月平面内周期解可以设计自然伴飞编队, 从而实现副星位于主星的前方或者后方的几米至几百千米的距离,沿一条局部振动的周期轨迹运动的伴飞。该编队适用于交会对接停泊轨道等自然伴飞任务。
3)设计DRO 附近的受控圆编队时,参考轨道方向应多考虑倾斜或垂直于xy平面的情况,有助于减少绕飞轨迹的燃耗;圆心则应设置在原点附近,以避免产生较大的燃耗;且由于线性化特性的存在,可以通过放缩某个尺度的转移结果得到其他尺度参考轨迹以及所需的燃耗,如此可以大大减小分析过程中的计算量。
4)本文所提出的安全转移编队可以实现任意两点之间的安全转移,在转移过程中可保证参考转移轨道上每一点距离主星有足够的安全距离。
