大跨度混合连续梁桥施工监控参数分析

2023-04-14张猛汤兴

科技与创新 2023年7期

张猛，汤兴

（中铁二十四局集团有限公司，上海 200433）

连续梁桥施工过程是一个复杂的系统工程。在实际施工过程中，桥梁的成桥状态容易受到桥梁自身材料性能差异、预应力损失等原因的影响，导致难以与理想的设计状态保持一致[1-4]。因此，需要了解参数对桥梁结构的影响关系，进而对施工监控关键参数进行敏感性分析，以便为桥梁施工误差的修正提供科学依据[5-6]。

文献[1]研究了拉索弹性模量、主梁重度、主梁刚度及索塔刚度等设计参数对全桥线形、内力的影响；文献[7]采用解析法修正空缆线形和有限元法模拟施工过程，研究分析了张拉前参数和张拉过程参数变化对成桥吊索力的影响；文献[8]研究了多塔矮塔斜拉桥参数变化对结构内力、变形和自振特性的影响。

由以上分析可以看出，相关学者针对桥梁结构参数的分析研究主要集中在悬索桥及斜拉桥等，针对连续梁桥的敏感性分析较少。因此，依托实际工程，从基础工作入手，开展混合连续梁桥的敏感性分析，对推进钢砼混合连续梁桥技术发展有着积极的现实意义。本文以某大跨度混合连续梁桥为研究对象，对施工监控关键参数采用有限元模型计算的方式进行敏感性分析，分析在相同的变化范围内，桥梁线形及应力受到施工监控关键参数的影响程度。

1 施工有限元仿真模型

1.1 工程概况

某大跨度混合连续梁桥主桥采用（40+80+180+80+40）m 钢砼混合连续梁，主跨180 m，主跨跨中为88 m的钢箱梁拼接，钢箱梁两侧采用钢混结合段与预应力混凝土箱梁连接，其主桥立面布置图如图1 所示。

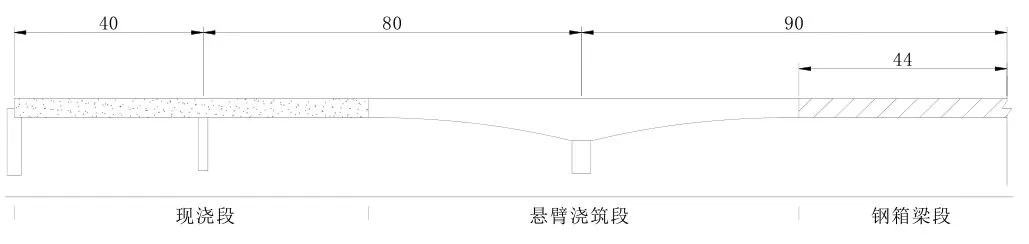
图1 某连续梁桥主桥1/2 桥跨立面布置图（单位：m）

主线桩号为ZK6+445.000—ZK6+865.000 段，在此段设置1 处平曲线，圆曲线半径为870 m。主桥最低点桩号为ZK6+865.000，标高为14.040 m，设计纵坡为1.113%，坡长为420 m。箱梁由预应力砼箱梁和钢箱梁组成，均采用单箱单室断面。主跨箱梁支点处梁高为9.1 m（以梁体中心线为准），跨中为4.1 m，梁底成1.8 次抛物线变化。箱底板宽为7.5 m，双侧对称悬臂为3 m，顶板全宽为13.5 m，桥面设3%单向坡。

1.2 有限元模型

采用有限元软件MIDAS/CIVIL 2019 建立梁单元模型，全桥共142 个单元、155 个节点。2 个0 号块各4 个单元，1—12 号块各1 个单元，中跨钢箱梁离散成29 个单元，如图2 所示。

图2 有限元计算模型

1.3 结构参数选取

在有限元模型中，影响桥梁结构的参数有很多，需要找到关键参数进行对应控制，通过查阅相关文献资料[9-10]，结合工程实际，本文选取考虑混凝土材料参数和预应力损失参数在最大悬臂阶段和成桥状态下对大跨度混合连续梁桥的影响[11-12]。在计算分析时采用控制变量法，即仅给定单一参数的变化幅度，其他参数保持不变，分别取标准状态下设计参数减小或增大10%进行分析。各设计参数的标准取值如表1 所示。

2 混凝土材料参数分析

2.1 混凝土容重分析

本工程采用的是C55 混凝土，按照规范其容重γ应取值为25 kN/m3，但是实际工程中混凝土容重会受到配筋的影响，因此其容重γ取值为26 kN/m3。为得到主梁线形和应力在最大悬臂状态和成桥状态下受到混凝土容重变化的影响，通过MIDAS/CIVIL 软件减小或增大10%的混凝土设计容重来进行分析。

2.1.1 对线形的影响

混凝土容重减小或增大10%时主梁挠度差如图3所示。由图可知，当混凝土容重减小或增大10%时，主梁挠度差分布大致对称，且具有类似的变化趋势。混凝土容重减小会导致主梁上拱，混凝土容重增大会导致主梁下挠，在悬臂梁端部附近挠度差最大，越靠近墩顶位置其数值越小。在最大悬臂阶段下，混凝土容重减小（增大）10%会导致主梁上拱（下挠），挠度差的最大值为8.417 mm，其变化幅度为19.61%；在成桥状态下，混凝土容重减小（增大）10%会导致主梁上拱（下挠），挠度差的最大值为6.403 mm，其变化幅度为15.1%。

图3 混凝土容重减小或增大10%时主梁挠度差

2.1.2 对应力的影响

混凝土容重减小或增大10%时主梁应力差如图4所示。由图可知，当混凝土容重减小或增大10%时，主梁应力差分布大致对称，且具有类似的变化趋势。在悬臂梁端部附近应力差最大，靠近跨中位置其数值逐渐减小。在最大悬臂阶段下，混凝土容重减小（增大）10%会导致主梁顶板产生压（拉）应力，应力差的最大值为0.6 MPa，其变化幅度为4.62%；混凝土容重减小（增大）10%会导致主梁底板产生拉（压）应力，应力差最大值为0.69 MPa，其变化幅度为33.5%。在成桥状态下，混凝土容重减小（增大）10%会导致主梁顶板产生压（拉）应力，应力差的最大值为0.6 MPa，其变化幅度为4.62%；混凝土容重减小（增大）10%会导致主梁底板产生拉（压）应力，应力差的最大值为0.67 MPa，其变化幅度为9.48%。

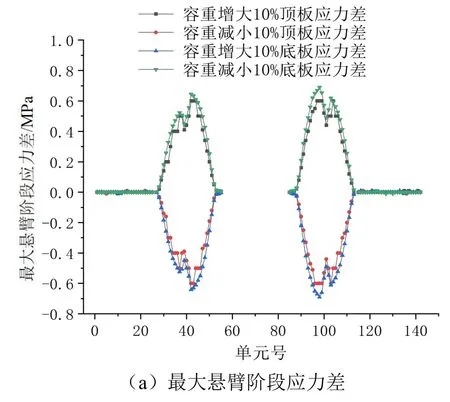
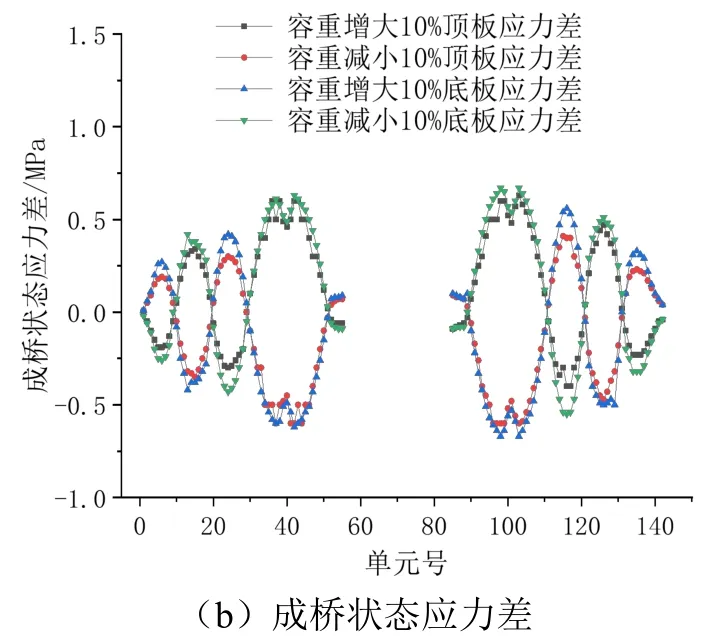
图4 混凝土容重减小或增大10%时主梁应力差

由以上分析可知，混凝土的容重变化对主梁的线形和应力影响都比较大。

抽取我校2012级护理专业一班和二班作为实验对象，均为女生，一班52人，二班53人，两班学生的年龄和基础学科成绩经统计学分析无显著性差异。设一班为对照组，二班为实验组。

2.2 混凝土弹性模量分析

本工程采用的是C55 混凝土，按照规范其设计弹性模量E应取值为3.55×104MPa。为得到最大悬臂阶段和成桥状态下弹性模量的变化对主梁线形和应力的影响，通过MIDAS/CIVIL 软件减小或增大10%的混凝土设计弹性模量来进行分析。

2.2.1 对线形的影响

混凝土弹性模量减小或增大10%时主梁挠度差如图5 所示。

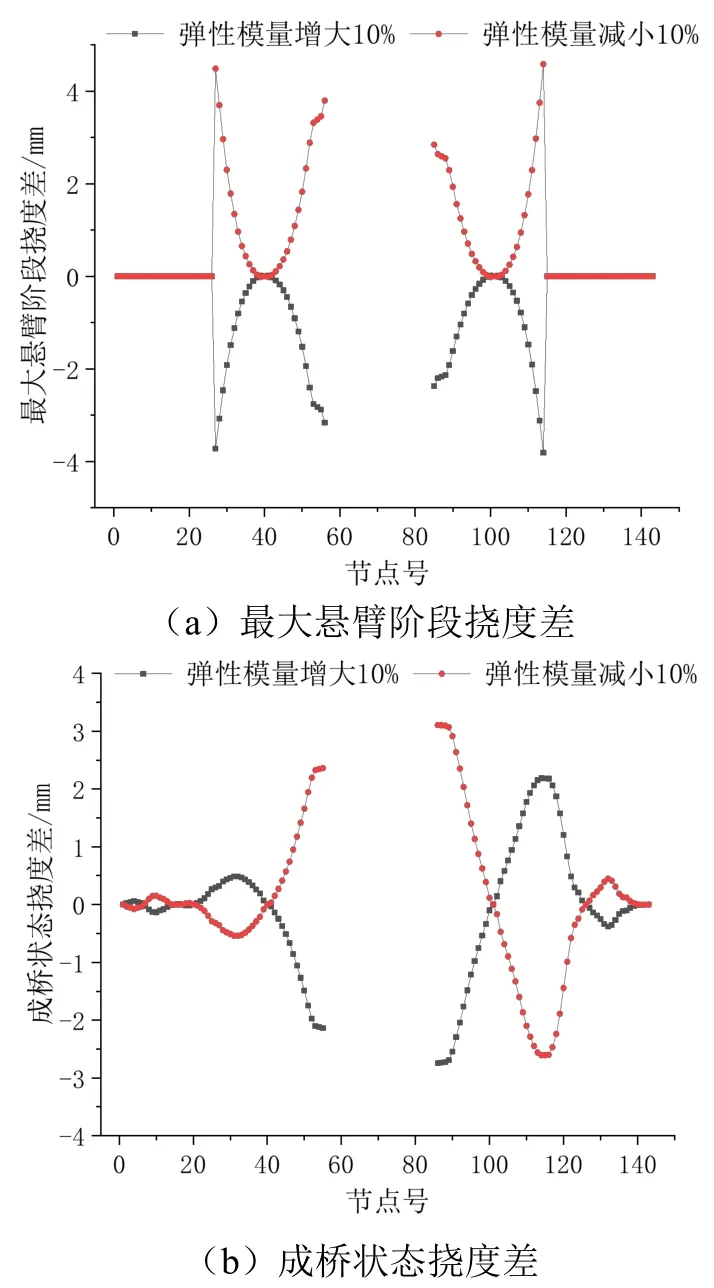
图5 混凝土弹性模量减小或增大10%时主梁挠度差

由图5 可知，当混凝土弹性模量减小或增大10%时，对主梁挠度差分布大致对称，且具有类似的变化趋势。随着混凝土弹性模量的减小主梁会出现一定的上拱现象，反之则会下挠，从墩顶位置到跨中其挠度差在逐渐增大。在最大悬臂阶段，弹性模量E增大10%，主梁挠度下挠变化的最大值为3.81 mm，其变化幅度为5.29%；弹性模量E减小10%，主梁挠度上拱变化的最大值为4.58 mm，其变化幅度为6.36%。在成桥状态下，弹性模量E增大10%，主梁挠度下挠变化的最大值为2.74 mm，其变化幅度为6.46%；弹性模量E减小10%，主梁挠度上拱变化的最大值为3.11 mm，其变化幅度为7.34%。

2.2.2 对应力的影响

混凝土弹性模量减小或增大10%时主梁应力差如图6 所示。由图可知，在最大悬臂阶段和成桥阶段，混凝土弹性模量增大或减小10%时，主梁的顶板和底板的应力变化最大值都小于或等于0.2 MPa，可以得出其变化幅度都小于2%。同时可以看出，顶板和底板的应力差的变化趋势是类似的，表明可以忽略它对主梁的应力影响。

图6 混凝土弹性模量减小或增大10%时主梁应力差

由以上分析可知，主梁的线形不易受到应力的影响，更易受到混凝土弹性模量的影响。

2.3 混凝土材料参数敏感性识别

为了得到桥梁受到不同参数影响程度的情况，采用参数敏感性分析的方法，对混凝土的材料参数进行敏感性分析。通过表格进行统计有限元模型在参数不用变化情况下的变化情况，统计结果如表2 和表3所示。

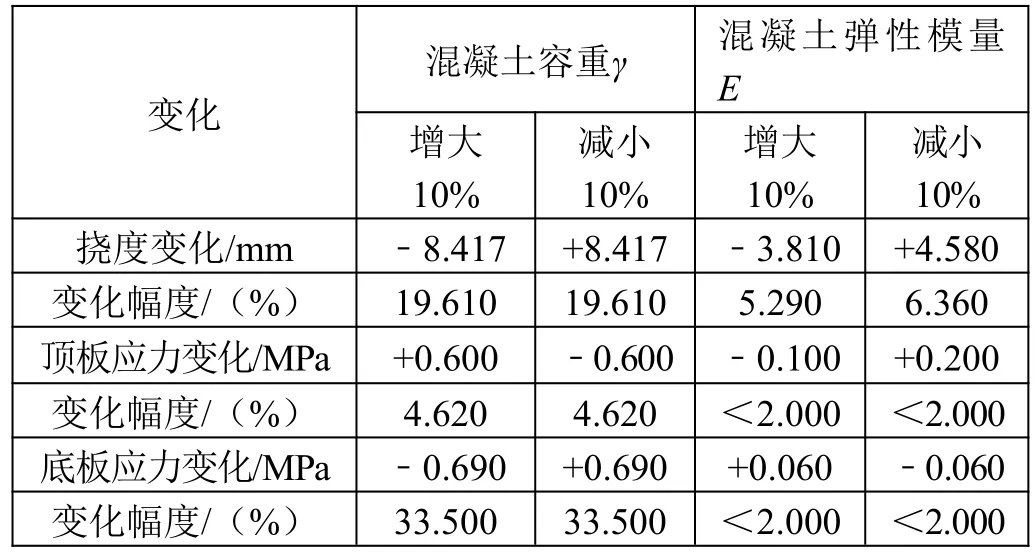
表2 最大悬臂阶段混凝土材料敏感性统计

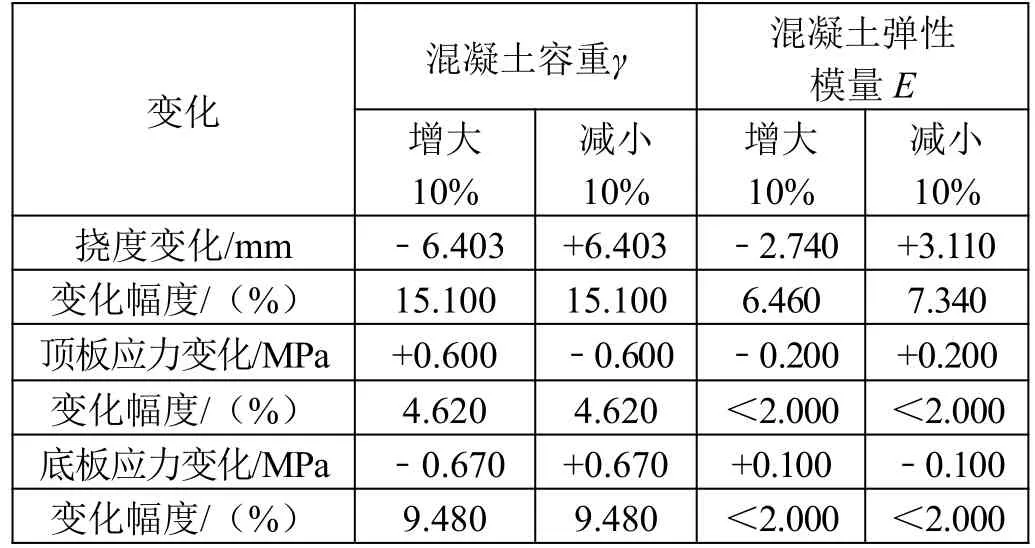
表3 成桥状态混凝土材料敏感性统计

由表2 和表3 的分析结果可知，主梁线形比主梁应力更容易受到混凝土弹性模量E的影响；但相较于受到弹性模量E的影响，主梁的线形和应力都更容易受到混凝土容重γ的影响。因此主梁线形的主要控制参数可以设定为混凝土弹性模量E和混凝土容重γ，主梁应力的主要控制参数可以设定为混凝土容重γ。为了减少施工带来的误差，在实际施工中需要对参数设计值进行及时修正，同时有限元模型也需要根据修正数值来进一步调整计算，因此需要对现场的混凝土试块进行取样实验。

3 预应力损失参数分析

大跨度混凝土桥梁在后期运营阶段，受到如车辆等移动荷载的作用以及混凝土自身收缩徐变的影响是造成跨中下挠情况出现的主要原因，同时预应力随时间变化的损失也是这种情况出现的重要原因[15-16]。在实际运营过程中，预应力损失包括预应力钢束与管道内壁的摩擦、管道局部偏差、钢筋回缩等情况，所以无法对预应力损失进行精确计算。

综合考虑，为了分析主梁线形和应力在最大悬臂阶段和成桥状态下的影响情况，选取并调整预应力筋与管道内壁之间的摩擦系数μ和管道局部偏差摩擦影响系数k这2 个系数大小的±10%。预应力筋与管道壁之间的摩擦系数和管道局部偏差摩擦影响系数的标准取值为μ=0.17，k=0.001 5 m-1。

3.1 对线形的影响

预应力参数减小或增大10%对主梁线形的影响如图7 所示。由图可以知道，μ和k这2 个参数减小或增大10%时，主梁挠度的上拱和下挠情况与参数μ和k的增大或减小成反比，并且具有类似的变化趋势，其挠度的变化值整体呈现对称分布。在最大悬臂阶段，主梁挠度差的最大值受到参数μ的影响的变化幅度小于1%，参数μ增大（减小）10%，主梁下挠（上拱）的挠度差最大值为0.47 mm；主梁挠度差的最大值受到参数k的影响的变化幅度小于1%，参数k增大（减小）10%，主梁下挠（上拱）的挠度差最大值为0.299 mm。

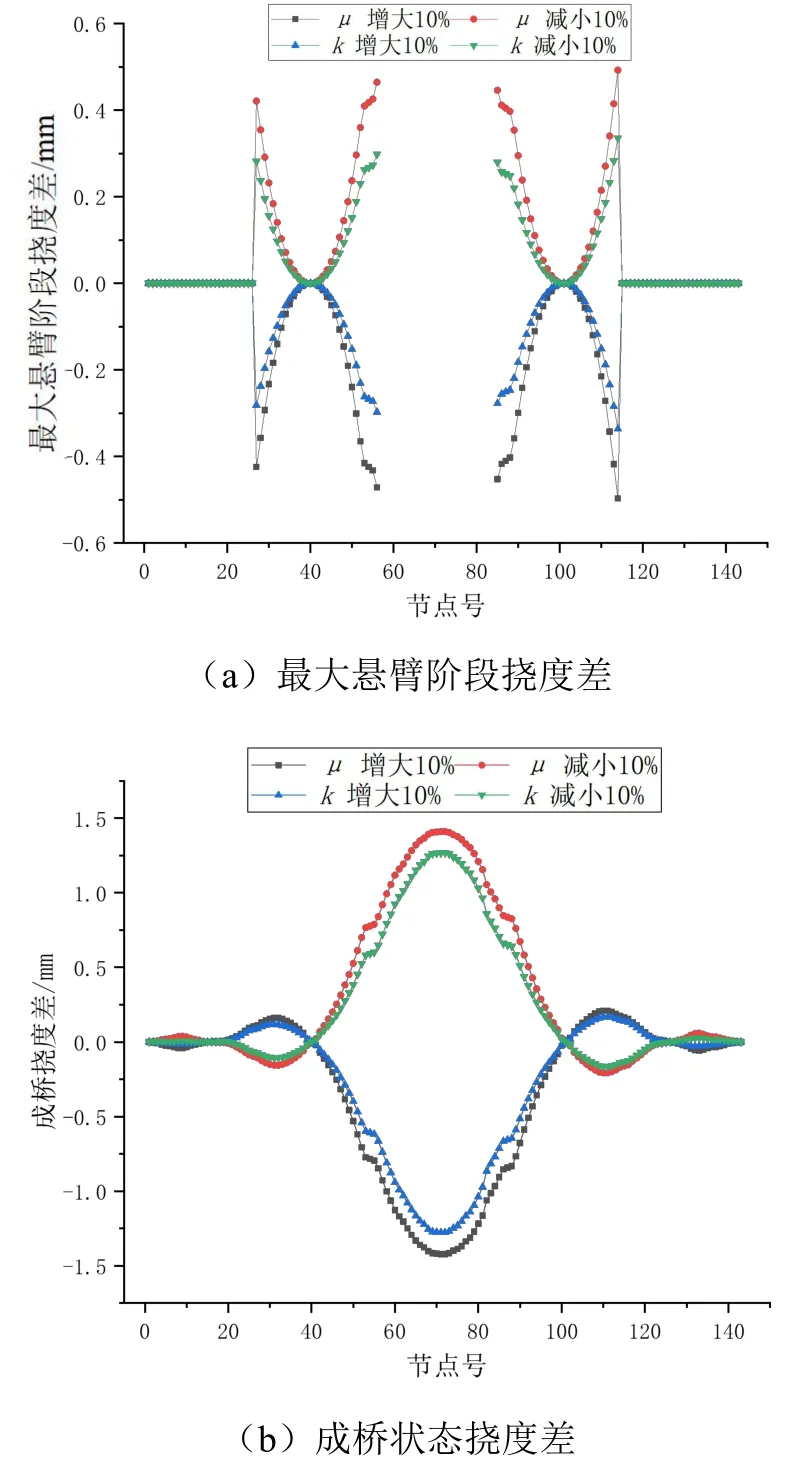
图7 预应力参数μ、k 减小或增大10%对主梁线形的影响

在成桥状态下，主梁挠度差的最大值受到参数μ的影响的变化幅度为3.55%，参数μ增大（减小）10%，主梁下挠（上拱）的挠度差最大值为1.42 mm；主梁挠度差的最大值受到参数k的影响的变化幅度为3.14%，参数k增大（减小）10%，主梁下挠（上拱）的挠度差最大值为1.27 mm。

由以上分析可知，预应力损失参数的变化对主梁线形的影响在成桥状态下比在最大悬臂阶段更大。

3.2 对应力的影响

在最大悬臂阶段和成桥状态下预应力损失增大会导致主梁顶板和底板受拉，减小则会导致顶板和底板受压，应力变化值具有相同的变化趋势且呈对称分布，如表4 和表5 所示。

表4 最大悬臂阶段预应力损失参数变化敏感性统计

表5 成桥状态预应力损失参数变化敏感性统计

在最大悬臂阶段，主梁顶板应力受到参数μ和k的影响的变化幅度接近，为0.7%左右，其变化最大值为0.1 MPa；主梁底板应力受到参数μ和k的影响的变化幅度为0.59%和0.44%，其变化最大值为0.03 MPa。在成桥状态下，主梁顶板和底板应力受到参数μ和k的影响的变化幅度在0.75%～0.96%之间，其变化最大值为0.1 MPa。

由以上分析可知，在最大悬臂阶段顶板应力受到的影响大于底板应力，究其原因为预应力钢束的张拉在悬臂施工阶段的主要部位为箱梁的顶板和腹板，因此顶板更容易受到应力的影响。综合以上可以看出，预应力损失参数μ和k的变化对应力的影响程度均较小，在成桥状态略大于最大悬臂阶段。

综上所述，在桥梁施工阶段，主梁线形和应力受到预应力损失参数μ和k的影响要远小于混凝土材料参数的影响；但是在实际使用阶段，预应力损失对桥梁结构线形和应力的影响会随着桥梁结构使用年限的增长而增大。因此，在实际工程施工控制的过程中，也需要对该参数进行现场测定，采用摩阻实验获得参数实际，代入有限元模型中进行及时修正，以确定最佳的理论值便于指导施工。