基于层次分析法的智能跟车功能评价模型研究

卢迪柯 周毅 何海燕

（同济大学汽车学院，上海 201804）

缩略语

TTC Time To Collision

THW Time To Headway

AHP Analytic Hierarchy Process

HP Highway Pilot

TJP Traffic Jam Pilot

NOP Navigator On Pilot

IVF Intelligent Vehicle Following

ACC Adaptive Cruise Control

FCW Forward Collision Warning

AEB Autonomous Emergency Braking

LDW Lane Departure Warning

BSD Blind Spot Detection

0 引言

随着智能驾驶技术的不断发展，特斯拉、上汽集团、蔚来、小鹏、理想等主机厂已经开发了许多较为完善的高级自动驾驶辅助系统，如高速自动辅助驾驶（Highway Pilot,HP）、拥堵驾驶辅助（Traffic Jam Pilot，TJP）、导航辅助驾驶（Navigator on Pilot,NOP）等。而在日常驾驶过程中，跟车行驶占据整个行车过程70%以上，目前对于智能跟车功能评价尚无统一的标准法规[1]，因此十分有必要开展智能跟车功能测试评价方法的研究，本文围绕智能跟车功能（Intelligent Vehicle Following,IVF）进行深入分析和总结。

（1）本文研究的智能跟车功能（IVF）指具备该功能的车辆在本车道内可跟随前方目标车辆自动调节车辆速度，并根据不同工况与前方目标车辆保持适当距离。

（2）研究国内外自适应巡航（Adaptive Cruise Con⁃trol，ACC）、前端碰撞预警（Forward Collision Warning，FCW）、自动紧急制动（Autonomous Emergency Braking，AEB）、车道偏离预警（Lane Departure Warning，LDW）、盲区探测（Blind Spot Detection，BSD）与跟车功能相关的测试标准[2-3]，基于其评价参数，并结合跟车功能相关实际经验，构建智能跟车功能综合评价体系。

（3）借助Delphi 专家咨询法对评价参数与安全性和舒适性的相关性进行评估。

（4）运用层次分析法设计递阶层次结构，并判断各评价指标的一致性，建立智能跟车综合评价体系模型，并对智能跟车功能测试评价的进一步发展提出研究展望。

1 评价指标体系构建

IVF系统评价一般是基于不同测试工况下的功能表现，即用客观参数对系统进行评分以量化其性能水平，但纯粹的客观参数分析法通常只针对单个参数进行衡量，不能对系统功能的总体表现进行有效评估，本文以主客观相结合的方式对智能跟车功能进行安全性与舒适性的研究。

1.1 评价指标体系框架

本文以智能跟车功能的测试评价为核心开展相关研究工作，一方面关注消费者的主观感受，另一方面也关注研发工程师更为在意的客观数据。为了设计一套可用于主客观评估的测试评价体系，结合消费者实际使用，拟定该评价体系从安全性、舒适性2个维度开展相关研究，所选择的基础评价参数均来自智能汽车功能评测标准，综合分析目标层、准则层和参数层，所建立的智能跟车功能综合评价指标体系如图1所示。

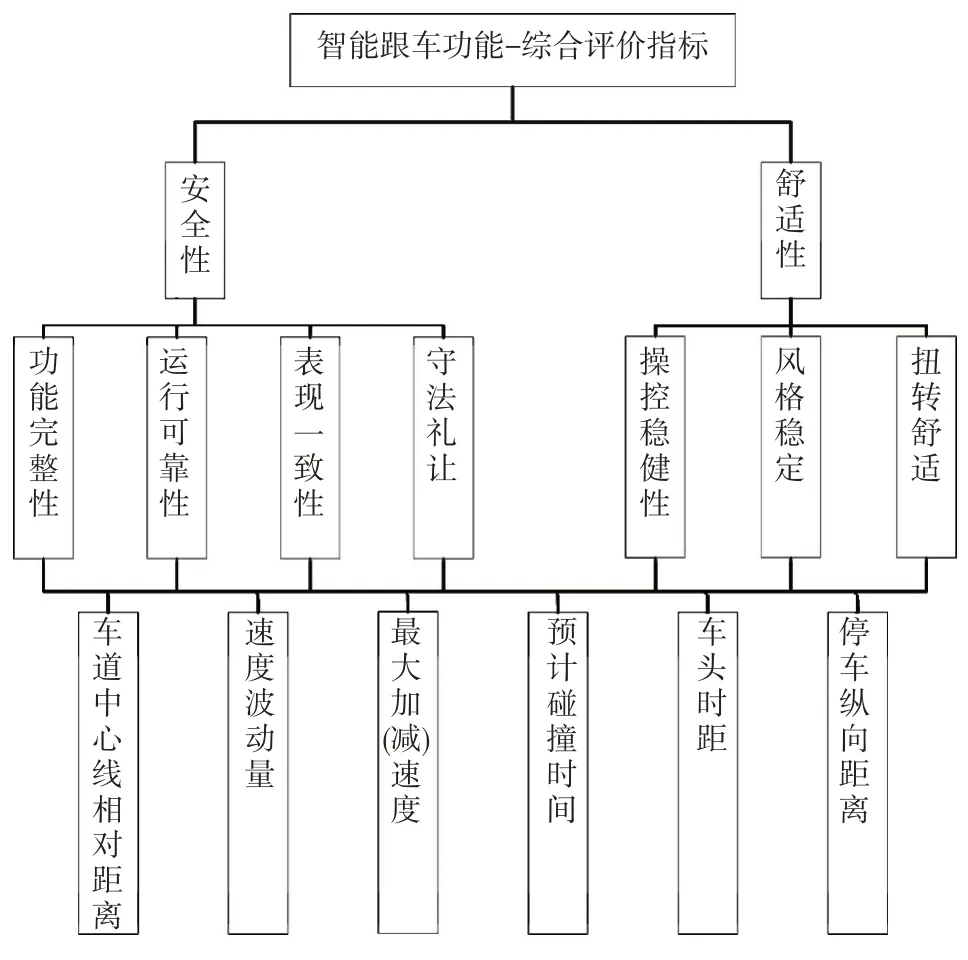
图1 智能跟车功能综合评价指标体系

1.2 评价参数计算方法及内涵

IVF 系统控制性能主要是分为2 方面：稳态性能和动态性能。其中，稳态性能主要分析被测车辆在匀速跟车工况下跟车距离、车速的稳定性。动态性能主要统计、分析车辆在跟车工况下加（减）速度的相关特性以及相关参数的精度。

（1）预计碰撞时间（Time To Collision，TTC）

TTC定义为本车与前车之间的相对距离除以相对速度，为了确保智能车辆运行安全可靠，要求TTC>0 s。

对于相对速度不变的情况，也就是说当2 车都没有加速或减速时，TTC为本车与前车发生碰撞的时间。TTC计算如下：

式中，XT为前车位置；XH为主车位置；LT为车身长度；vH为主车速度；vT为前车速度。

（2）车头时距（Time Headway,THW）

为了更好地评估车辆行驶过程中的跟车距离，引入车头时距作为本文评价模型的一个重要参数。THW是一个表征驾驶员跟车行为的重要参数，定义为前后2 车头部通过道路某一断面的时间间隔[4]。THW值越小，表明主车跟随前车辆行驶过程中，当遇到紧急突发状况时，发生碰撞的概率越高，如跟车距离较小或主车速度较高的情况。THW计算如下：

式中，XT为前车位置；XH为主车位置；LT为车身长度；vH为主车速度。

2 评价参数的相关性评估

Delphi 法又称专家调查法，其本质是一种反馈匿名函询法[5]。根据研究目标，将需要专家进行判断的问题制定成调查问卷，本文通过线上匿名方式进行专家意见征询，充分确保参评专家自由发表意见，并尽可能保证其不受其他权威专家意见影响。

在完成首轮专家意见收集后，经过数据汇总、整理和分析，将分歧较大的问题进行重新梳理，并再度征求意见，直至取得一致意见。经过2轮征询和意见收集后，最终结果较为客观且可信。

2.1 专家遴选

本次调查经过两轮专家咨询，共计遴选了15位具有专业性和权威性的专家组成本研究的Delphi 法专家小组，其中5位来自同济大学相关学科，7位来自汽车主机厂（智己汽车、泛亚汽车技术中心、上汽大众），3 位来自智能驾驶相关零部件企业（舍弗勒、地平线、千顾汽车）。专家小组成员均多年从事智能驾驶技术开发或测试技术研究与实践，工作单位涵盖相关性较强的高校和企业，具有广泛的代表性。

根据评价指标体系框架，编制专家咨询表，内容包括专家的基本情况、对指标相关性的判断依据、熟悉程度。专家采用背对背的形式填写问卷，对初步评价指标体系内各评价参数对“安全性”和“舒适性”的相关性进行打分，评分值用李克特量表（5-Likert scale）进行评定[6]，具体评分见表1所示。

表1 李克特量表相关性

2.2 评价指标相关性筛选

2.2.1 专家积极系数

该系数用于衡量专家对咨询内容的关心程度，以有效咨询表的回收率来衡量，公式如下：

本次调研共计发放咨询表15 份，均在7 天内收回，有效回收率为100%，表明所调查专家对该项目高度支持，积极性较高。

2.2.2 专家权威程度以专家权威系数Cr来衡量，公式如下：

式中，Ca为专家对指标的判断系数，专家基于表2 自评得出；Cs为专家对指标的熟悉程度系数，专家基于表3自评得出。

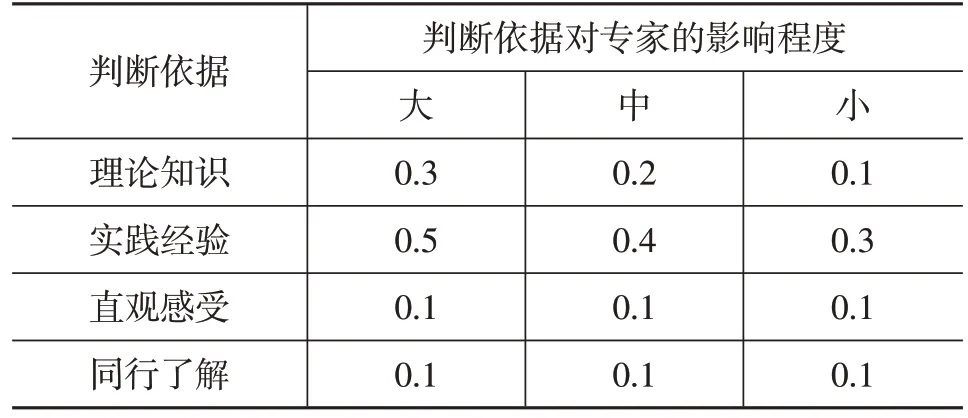
表2 专家判断依据及影响程度

表3 专家熟悉程度

经过对专家自评结果分析，Ca=0.95，Cs=0.88。专家权威系数Cr=0.92，专家权威程度较高，可为本次相关性分析提供可靠的评判依据。

2.2.3 专家意见集中程度

满分频率fj的计算公式如下：

式中，Nj表示参加第j个指标相关性评价的专家数；表示其中打满分的专家数。fj的取值范围为[0,1]，可作为的补充指标。

2.2.4 专家意见协调程度

通常用变异系数CV来衡量，可表示专家对各项指标的认同程度。变异系数CV表示n个专家对第j个指标的协调程度，计算公式如下：

通过2 轮Delphi 法的专家调研筛选，最终调研结果详见表4和表5。

表4 “安全性”与指标相关性专家咨询结果

表5 “舒适性”与指标相关性专家咨询结果

以同时满足重要性赋值均数≥3.5，且变异系数≤0.24 两项条目作为筛选标准，在基础评价参数中，与安全性相关性比较高的参数包括车道中心线相对距离、速度波动、最大加（减）速度、预计碰撞时间和车头时距；与舒适性相关性比较高的参数包括最大加（减）速度、车头时距和停车纵向距离。根据安全性和舒适性相关参数指标，利用层次分析法确定各指标参数与总目标的权重系数。

3 指标权重的计算方法

运用评价指标体系的若干个指标参数对智能跟车功能进行综合评价时，不同指标的重要程度有所不同，为了能够合理地描述各层级不同指标在评价过程中的作用地位和重要程度，需要明确各指标的权重系数，从而能够得到智能跟车功能综合水平。

结合本文建立的智能跟车功能的评价指标体系，借助Delphi 专家问卷调查法已经完成安全性和舒适性相关可量化指标参数，然后将基于专家意见并运用层次分析法确定各指标权重系数。

层次分析法（Analytic Hierarchy Process，AHP）是一种将定性分析和定量计算相结合的、具有层次结构的多目标决策方法[7]。利用层次分析法构建的理论模型将为智能跟车评价指标的选取和评价体系的建立提供完整的方案路线，并为多维度指标的统一化表达提供理论依托，主要步骤包括建立决策问题的递阶层次结构、构造两两判断矩阵、层次单排序及其一致性检验和层次总排序，针对智能跟车功能综合评价指标体系，获取各指标权重的计算方法，主要计算步骤如下。

3.1 构造判断矩阵

基于图1 所建立的递阶层次结构，上下相邻层次间元素的隶属关系即被确定，根据上层目标，在确定下一层不同元素权重时，采用两两比较的方法，指在准则Ck下，对它所支配的元素A1、A2……An中任意2 个元素Ai和Aj进行比较，它们中哪一个更重要、重要性为多少。本文按照9级比例标度，标度值及含义详见表6。基于Delphi 表3和表4的-xj、fj和CV值作为依据，安全性、舒适性及其相对于总目标的判断矩阵分别如下表7、表8和表9所示。

表6 “9级比例标度”标度值及含义

表7 基于标度值的“安全性”判断矩阵

表8 基于标度值的“舒适性”判断矩阵

3.2 层次单排序及其一致性检验

层次单排序是指在目标层或准则层各元素Ck的支配下，n个元素排序权值的计算问题。两两比较判断矩阵的最大特征值对应的特征向量就是该准则支配下的各元素排序权值，设(ω1,ω2…ωn)Tt是判断矩阵最大特征值对应的特征向量，归一化之后就是n个元素A1、A2……An的排序向量[8]。

由定理“n阶正互反矩阵是一致性矩阵的充要条件，它的最大特征根是γmax=n”可知，当判断矩阵不一致时，γmax>n，误差越大γmax-n的差值就越大。本文两两比较判断矩阵，依据多位专家咨询结果给定，但判断的不一致性仍然可能存在，为了更好地避免不一致性问题，引入一致性比例（Consistency Ratio,CR）值作为判断矩阵是否具有一致性的检验标准，其计算公示如下：

式中，RI为随机一致性指标，具体数值详见表10。

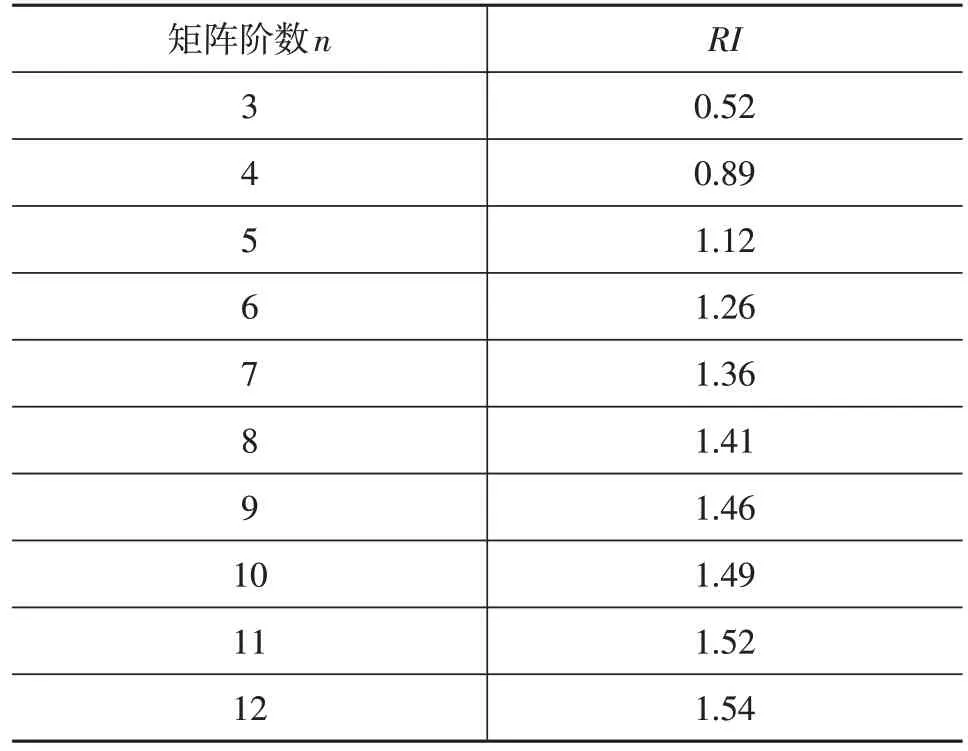
表10 随机一致性指标RI

针对以上表7、表8 和表9 中3 个判断矩阵，分别计算其最大特征值对应的特征向量，并对其进行归一化处理，可计算得出该判断矩阵对应的单排序向量，如表7、表8和表9最后列ωi所示。当计算得到CR值小于0.1 时，认为判断矩阵具有一致性，否则，应当对判断矩阵中的数值进行修正，再进行一致性检验，直到满足CR<0.1的要求为止。经检验，以上3个判断矩阵均满足一致性检验。

3.3 层次总排序

层次总排序是要得到递阶层次结构中，最低层次中的所有元素对于智能跟车功能总目标的相对权重。经计算，各个指标参量相对于智能跟车功能综合指标的权重系数如表11所示。

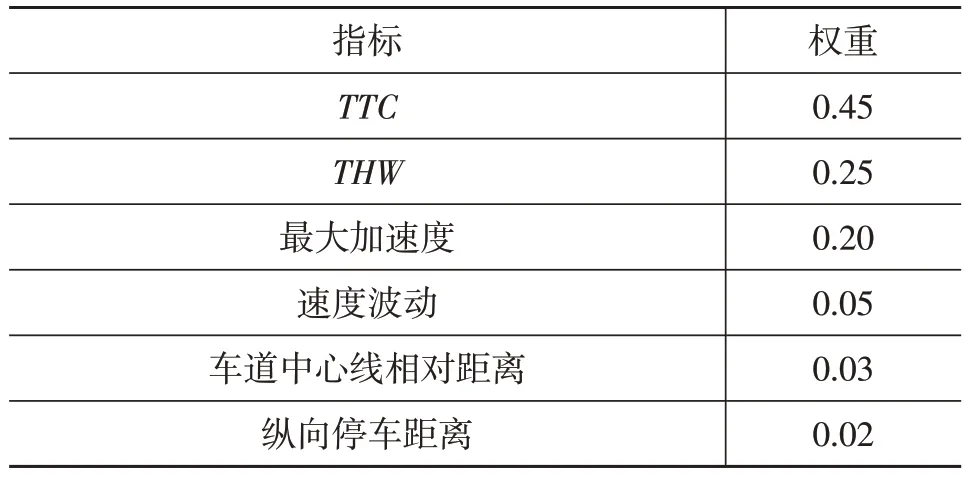
表11 指标权重系数

4 评价模型应用

针对评价模型内各项指标，基于智能跟车功能要求，确定单项指标评分标准及其单项满分值。选定某车型作为被测车型，进行测试并采集数据，借助该模型对其智能跟车功能进行评分。

4.1 指标评分标准

（1）THW

行驶的期望安全距离与车速成正比，为了更好地获取THW阈值，假定车辆遇到紧急情况时，其最大减速度为6 m/s2，分别计算系统在无需反应时间及需要反应时间2种情况下的跟车时距（表12）。

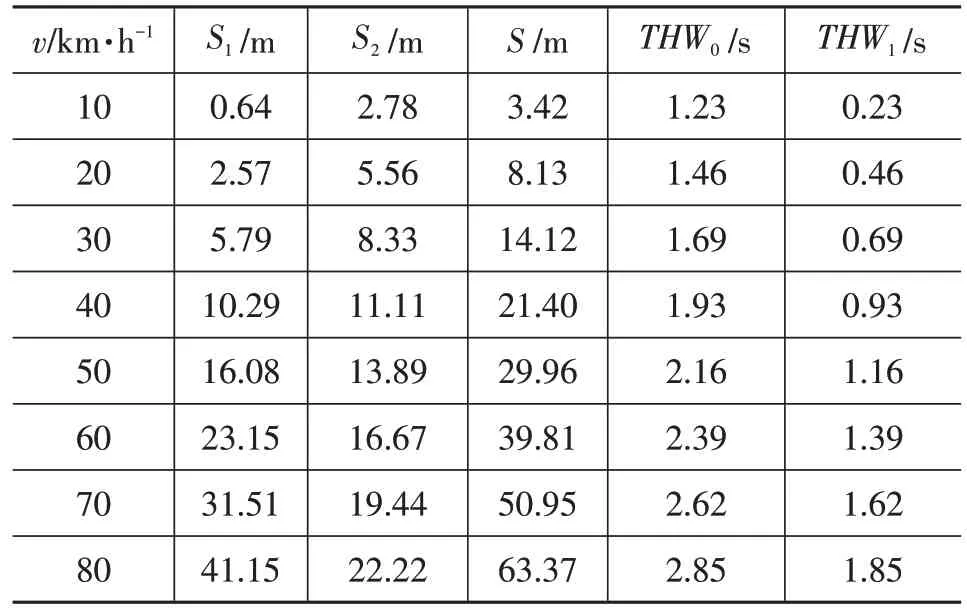
表12 最大减速度为6 m/s2时THW阈值

安全跟车距离S的计算公式如下：

式中S1为不含制动系统反应时间的制动距离；S2为包含系统反应时间的制动距离。

安全跟车情况下（系统需要反应时间）的跟车时距THW0计算公式如下：

式中，v为车速。

假定系统无需反应情况下的跟车时距THW1的计算公式如下：

（2）TTC

TTC直接决定车辆是否发生碰撞，所以在该评价模型中，该值作为“一票否决制”。当|TTC|=0 时，该车跟车功能总评分为0 分。针对不同的车速，其TTC阈值不同，详见表13。

（3）指标评分标准

针对智能跟车功能相关的各项指标，评分体系满分采用100 分，各项指标评分标准及相应满分分值如表14所示。

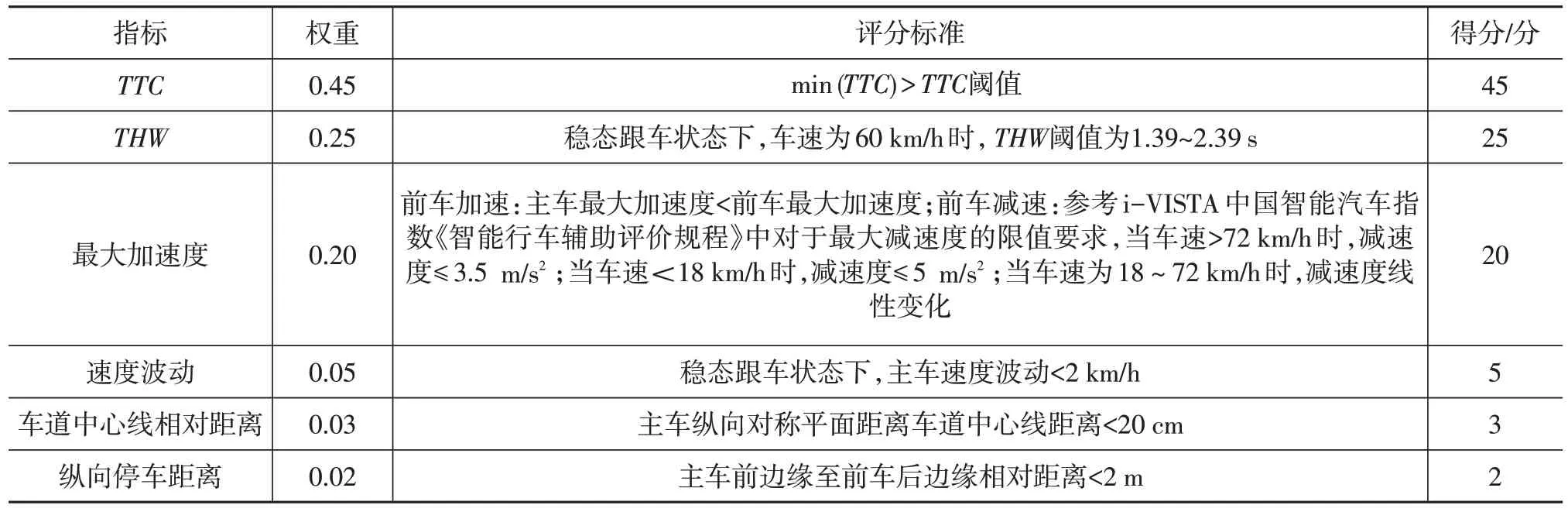
表14 各项指标评分标准及分值

4.2 评价实施

针对跟车过程，前车的纵向运动形态分为3种：匀速、减速和加速。本次测试过程主要选取某车型作为主车，进行了前车“加速—匀速”场景测试，其主要参数如图2所示。

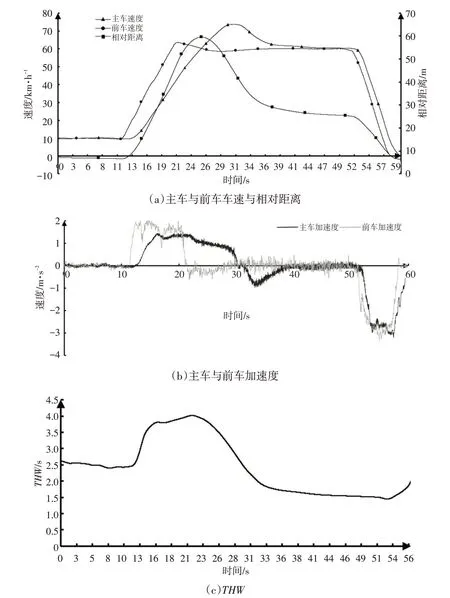
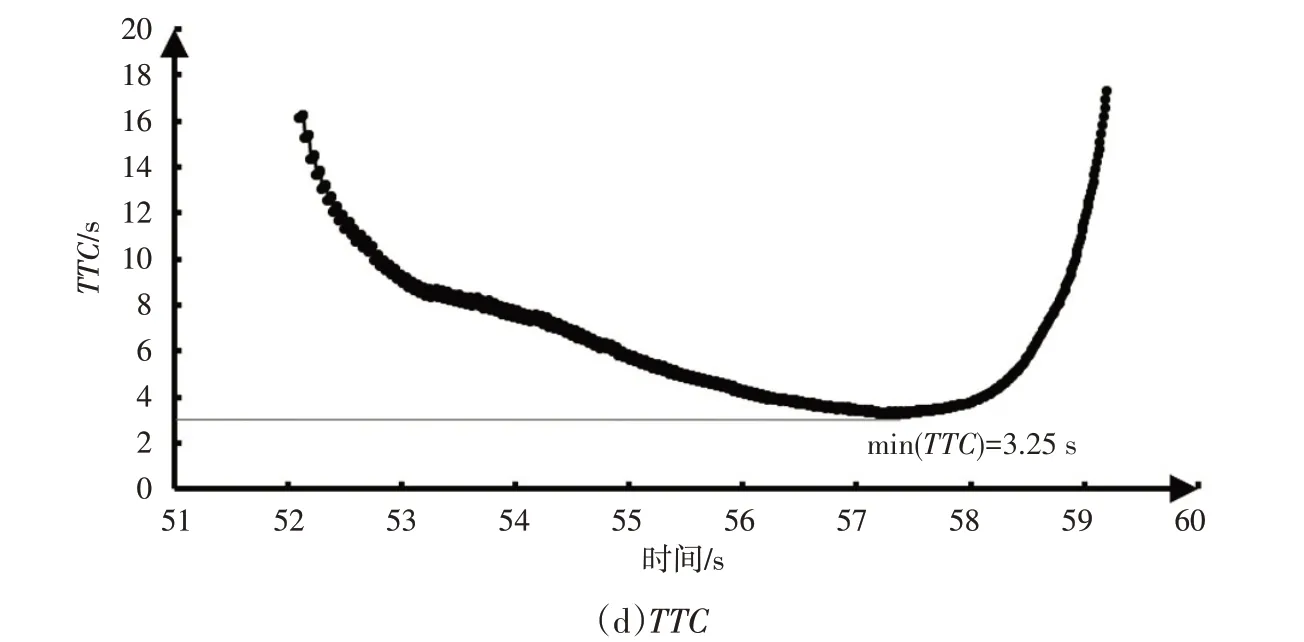
图2 被测车辆主要参数

基于表14各项指标评分标准及分值，并结合该车辆所有参数，其最终得分如表15所示。

表15 被测车辆评分结果

该车型总体得分为91分，该车型智能跟车功能表现良好。

5 结语

高级驾驶辅助功能测试评价是开展技术研发和工程化应用的重要环节，本研究从智能跟车功能的安全性和舒适性方面，并分别选取功能完整性、运行可靠性、表现一致性、守法礼让、操控稳健性、风格稳定和氛围舒适多个评价子维度。基于预计碰撞时间(TTC)、车头时距（THW）、最大加（减）速度、速度波动量、车道中心线相对距离和纵向停车距离作为评价指标参数，利用层次分析法（AHP）和德尔菲法（Delphi），本文设计了一套综合评价模型，主要创新点如下：

（1）评价框架：设计了以智能跟车功能安全性和舒适性为评价准则的递阶层次结构，通过建立智能跟车综合评价指标模型，实现智能跟车功能评价体系的多维度解读。

（2）评价指标：以智能跟车功能相关的标准法规为依托，尽可能多地采用客观参数，构筑评价模型。

（3）赋权方法：通过德尔菲（Delphi）法调研多位业内专家，有效降低了层次分析法在构筑判断矩阵时受人为因素干扰。

声明：本文在进行专家问卷调查时，所邀请的专家均为相关企业内资深工程师，且与本文作者无任何利益关系。