巧用极值法 优化初中物理解题
2023-04-10李文学
李文学
(江苏省南通市崇川初级中学,江苏 南通 226014)
物理知识理论性强、涉及学科广,对学生的知识、思维要求比较高.尤其是“物理核心素养”的提出,要求教师在组织课堂教学时,不再局限于理论知识的灌输,更加关注学生的物理思维、问题解决能力,真正实现学生的全面发展.解题作为初中物理教学的重要组成部分,不仅考查物理理论知识掌握情况,也反映了知识的迁移和应用能力.鉴于此,在日常物理教学中,积极渗透物理解题方法,引导学生在快速准确解题过程中促进知识内化、思维发展,已经成为当前物理教学的重要组成部分.
1 初中物理极值解题法教学概述
极值法又被称之为极端假设法、极限法等.极值法就是将问题中某个变量取最大值、最小值,或者某一个定值时,通过分析所得出来的结论,最终完成问题的解答.在初中物理学习中,伴随着所学内容的增加,以及题目难度的加大,当常规解题方法受限时,可巧妙运用极值法,在打开学生解题思路的同时,也实现了物理题目化繁为简、化难为易,使得物理解题更加高效.同时,在运用极值法解题的过程中,进一步开阔了学生的思维,有助于帮助其形成跨学科思维,使其意识到极值解题法不仅仅局限于物理学科中,还可灵活应用到其他学科中,真正实现了学生的全面发展.因此,从这一角度上来说,积极开展极值法教学,是提升学生物理解能力的必然选择,更是促进学科素养的有力途径[1].
2 极值法在初中物理解题中的应用
2.1 极值法解决液体压强问题
“液体压强”是初中物理中非常重要的知识点,也是考试的重点.针对这一类型的题目,如果按照常规解题思维,将面临着繁琐的步骤.而通过极值法,则可巧妙避开常规解题思路中的诸多物理量分析,直接得到答案,极大地提升了学生的解题效率.
例1如图1所示,有两个完全相同的量筒,其中一个量筒中盛有水,另外一个量筒中盛有酒精.已知酒精和水的质量相同,且两个量筒中M、N到量筒底部的距离也相等.假设两点处的液体压强分别为PM、PN.PM与PN的大小关系正确的是( ).
A.PM
C.PM=PND.无法确定


图1 探究不同液体中同一高度处压强
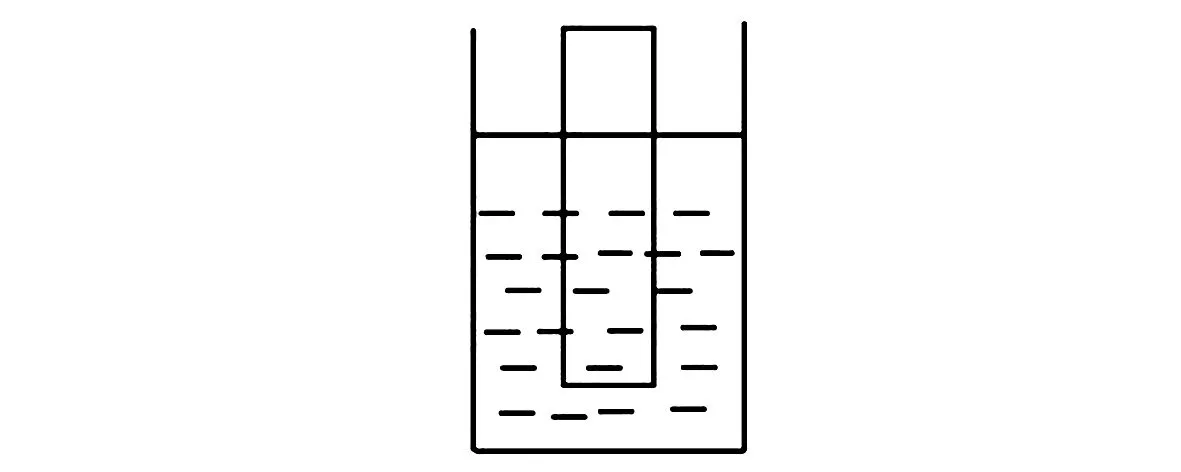
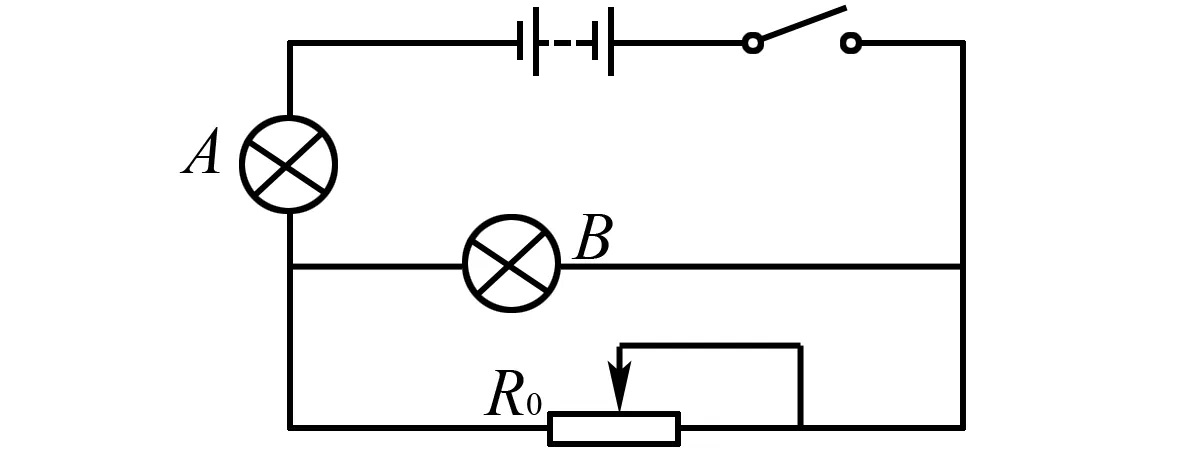
但是巧妙运用极值法,可简化解题过程,避免诸多物理量分析.在极值法解题中,由于题目中没有给出M、N两点的位置,只说明两者到量筒底部的距离相等.此时,即可将M取在水面上,此时水所产生的压强为0;而对于N点来说,由于其到量筒底部的距离与M点相同,则N上方依然存在酒精,此时其压强显然大于0.由此可得出PM 综合上述两种解题思路不难发现,常规解题思路虽然能够获得正确的答案,但学生在解题时,需要围绕液体体积、质量、压强等物理量展开精准地分析,方可得到正确的答案.而通过极值法则可巧妙避开这些繁琐的分析,进一步提升了物理解题效率. “杠杆平衡”是初中物理中一个常见的考点,题目虽然非常多,但基本上都是判断其平衡方向.经解题实践证明,适当运用极值法,使得题目分析更加透彻,解题速度也随之提升. 图2 杠杆平衡示意图 例2如图2所示,杠杆处于平衡的状态下,如果将图中的物体A和物体B分别向支点的方向移动相同的距离,则杠杆会出现的状态是( ). A.杠杆仍然平衡 B.不能平衡,向A端倾斜 C.不能平衡,向B端倾斜 D.条件不足,无法判断 解析按照常规的解题思路,学生需要结合相关的公式进行判断,即:mAgL1=mBgL2,L1 而通过极值法则可有效避免“力矩变化关系”分析,将原本复杂的问题简单化,即:由于题目中并未直接给出规定的移动距离数值,学生可任意取值.此时,即可将物体A直接移动到O点,此时物体A的力臂、力矩为0;而对物体B来说,其力臂和力矩明显不为0.此时杠杆必然会向B端倾斜,选项C正确[2]. “浮力”也是初中物理的重要知识点,也是常考的内容之一.在这一部分知识中,部分问题学生按照常规的思维很难完成.而运用极值法可快速求解. 例3将一个20N的空心铁球浸入到水中,则铁球会在水中出现的状态是( ). A.上浮 B.下沉 C.悬浮 D.以上均有可能 解析这一题目条件比较少,有关铁球体积、空心部分体积都没有提到.此时,如果常规的解题思路,根本无法对铁球的状态进行判断.运用极值法进行分析:由于铁球空心部分体积未知,因此本题目可分为三种情况:其一、铁球空心部分体积比较大,此时铁球一定处于上浮的状态;其二,铁球空心部分体积比较小,此时整个铁球类似于实心状态,必然会出现下沉的状态;其三,空心部分体积恰好位于某一个数值中,此时就可能出现悬浮的状态.因此,综上所述,本题目的正确答案为D选项. 图3 物体在水中状态示意图 例4如图3所示,一个密度均匀的木板漂浮在水面上,如果在水面虚线处将其截掉,则剩余的木块会出现什么样的变化? 解析在本题目中,如果按照常规的思维进行解题,需要先对水中的木块进行受力分析.之后,结合木块截掉前后的受力分析结果,得出浮力与木块的重力相等,即F浮=ρ水gV排.根据这一公式,木块截取之后,木块排水的重力大于自身的重力.截取之后,新木块重力大于浮力,自然会出现下沉现象. 鉴于常规解题中的繁琐步骤,可充分利用极值法,将题干中的信息进行扩大,使其变“将水面以下的木块截去”.此时,木块的排水量体积为0,则木块在水中受到重力的作用,自然会出现下沉的现象[3]. 电学是初中物理的重要组成,在解答这一部分问题时,由于初中生初次接触电学知识,理论知识掌握情况不佳,无法精准把握电流、电阻和电压之间的关系.尤其是当电路问题中出现电阻串联、并联、滑动变阻器时,就给学生的解题带来了极大的困难.面对这些问题,即可巧妙融入极值法进行解答. 例5如图4所示,在本电路中,A、B两盏灯均可发光.如果将滑动变阻器R0的滑片向左移动.此时,对A、B两盏灯的亮暗变化情况进行判断. 图4 等效电路示意图 解析结合电学知识,当滑动变阻器R0的滑片向左移动时,致使B和滑动变阻器构成的并联电路中总电阻逐渐减少,则B灯出现了逐渐变暗的现象.而对于A灯来说,则因为回路中总电阻减少,导致其电流增加,A灯的逐渐变亮.在常规解题思路中,学生必须要按照动态的原则进行分析,对于初中阶段的学生来说,存在一定的难度. 鉴于此,借助极值法进行解答:由于题目中并未明确说明将滑片移动何处,按照极值法的内涵,将其滑到最左边.此时在整个电路中,B灯就会出现短路完全熄灭的现象.而A灯则会变得更亮.如此省去了动态化的分析,使得解题难度降低.可见,在本题目中,通过极值法的应用,直接揭示出问题的本质,在提升学生解题效率的同时,也促进了物理思维的发展[4]. 结合初中物理解题实践证明,通过极值法在课堂上的应用,实现了物理问题由繁到简、由难到易,真正提升了学生的解题效率.鉴于此,教师在组织课堂教学时,应通过有意识地引导,强化学生极值法解题意识,提升极值法解决问题的能力.首先,基于课堂教学引导学生利用极值法.在培养学生运用极值法解题时,不仅要加强基础知识教学,还应为学生提供一些相关的例题,通过带领学生在极值法解决实际问题中,逐渐掌握这一解题技能;其次,加强极值法解题联系.学生的解题能力并非一蹴而就,唯有经过一定的练习,才能在训练中完成极值法解题技巧的内化和应用.在日常解题教学中,不仅仅要在课堂上给学生提供大量的例题,还应在教学之余为学生布置针对性的练习,以便于学生在反复训练中,掌握极值法解题的要领;最后,加强题目类型总结,促使极值法灵活运用.初中物理知识点繁杂,且题目类型比较多,极值法在不同题目的应用也有所不同.在日常初中物理解题教学中,还应充分发挥教师的引导作用,围绕不同题目类型进行归类和极值法解决力学问题、极值法解决电学问题、极值法解决压强问题等,促使学生在归类分析中,真正掌握这一解题技巧的内涵,并促使其灵活应用[5]. 综上所述,极值法是解决初中物理问题的重要方法之一,将其应用到物理解题中,真正促进了物理解题由繁到简、由难到易,有效避免了解题过程中诸多物理量的分析,显著提升了学生的解题效率.鉴于此,初中物理教师在日常教学中,应基于极值法的内涵,将其灵活应用到不同类型的题目中,使得学生在极值法的辅助下,缩短解题时间,并开阔自身的解题思维,真正满足学科素养下的物理解题需求.2.2 极值法解决杠杆平衡问题

2.3 极值法解决浮力问题
2.4 极值法解决电学问题
3 初中物理极值解题法教学启示
