一道教材习题的演变
2023-04-07李梦娜
李梦娜

方程是刻画现实世界数量关系的有效模型,能够解决数学与实际生活中的问题,也是中考重点考查的知识点之一。这类题综合性强,常常由教材习(例)题演变而来,现举一例供同学们参考。
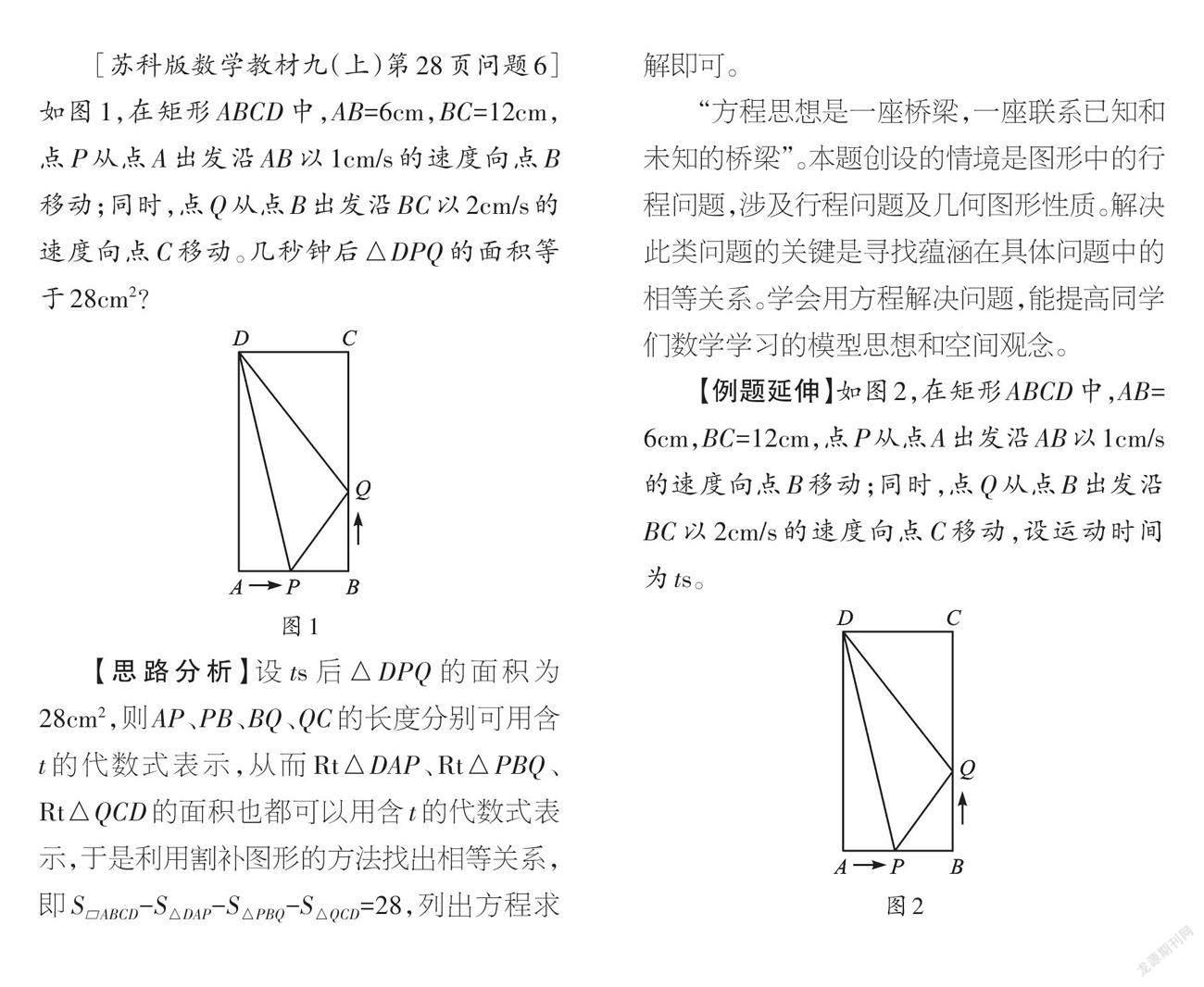
[苏科版数学教材九(上)第28页问题6]如图1,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿BC以2cm/s的速度向点C移动。几秒钟后△DPQ的面积等于28cm2?
【思路分析】设ts后△DPQ的面积为28cm2,则AP、PB、BQ、QC的长度分别可用含t的代数式表示,从而Rt△DAP、Rt△PBQ、Rt△QCD的面积也都可以用含t的代数式表示,于是利用割补图形的方法找出相等关系,即S▱ABCD-S△DAP-S△PBQ-S△QCD=28,列出方程求解即可。
“方程思想是一座桥梁,一座联系已知和未知的桥梁”。本题创设的情境是图形中的行程问题,涉及行程问题及几何图形性质。解决此类问题的关键是寻找蕴涵在具体问题中的相等关系。学会用方程解决问题,能提高同学们数学学习的模型思想和空间观念。
【例题延伸】如图2,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发沿AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿BC以2cm/s的速度向点C移动,设运动时间为ts。
(1)当t=2时,△DPQ的面积为 cm2;
(2)在运动过程中,△DPQ的面积能否为26cm2?如果能,求出t的值,若不能,请说明理由;
(3)运动过程中,当A、P、Q、D四点恰好在同一个圆上时,求t的值;
(4)运动过程中,当以Q为圆心、QP为半径的圆,与矩形ABCD的边共有4个交点时,直接写出t的取值范围。
【思路分析】第(1)问,根据运动速度和时间表示出线段长度,然后计算出三个直角三角形的面积,再用割补图形的方法就能得到△DPQ的面积,这一问与教材上的问题所用方法完全相同;第(2)问,根据(1)中的面积计算方式,列出关于t的方程,通过判断方程有无解即可得出答案;第(3)问,部分同学可能感觉下手困难,我们不难通过△DAP是直角三角形发现,经过点D、A、P的圆的直径就是DP,根据点Q也在圆上,那么∠DQP=90°,先分别表示出DP、DQ、PQ,再利用勾股定理DP2=DQ2+PQ2,列出方程求解即可;第(4)问,我们可通过多画草图,判断出⊙Q与边AD相切和⊙Q经过点D是⊙Q与矩形的边有4个交点变成3个交点的临界情况,再根据半径相等列出关于t的方程求解。
本题考查了矩形的性质、点与圆的位置关系、三角形的面积、圆的切线等知识点,综合性較强,熟练利用勾股定理列出一元二次方程是解题的关键。
【中考题】(2021·山东日照)如图3,在矩形ABCD中,AB=8cm,AD=12cm,点P从点B出发,以2cm/s的速度沿BC边向点C运动,到达点C停止,同时,点Q从点C出发,以vcm/s的速度沿CD边向点D运动,到达点D停止,规定其中一个动点停止运动时,另一个动点也随之停止运动。当v为 时,△ABP与△PCQ全等。
【思路分析】设P、Q两点均运动ts,则BP、PC、CQ的长度分别可以用含t的代数式表示。而△ABP与△PCQ全等有两种情况:
①△ABP≌△PCQ,此时BP=CQ,AB=PC,可得12-2t=8,解出t=2,相应得到v=2;
②△ABP≌△QCP,此时AB=QC,BP=CP,可得2t=12-2t,解出t=3,相应得到v=[83]。
综上可得,v为2或[83]。
本题主要考查了全等三角形的判定和性质、矩形的性质、分类讨论和方程思想的应用。解答本题时需注意三角形全等的对应关系,分情况讨论。
数学大师陈省身先生曾经说过:数学有“好”数学和“不大好”数学之分。方程,就是“好”的数学的代表,它是最基本的解题方法之一,也是同学们解题时重要的抓手。
(作者单位:江苏省泰州市高港实验初级中学)
