一种舰载低信噪比环境下的音频端点检测算法

王中正，王 鉴,韩 焱,韩星程

(1.中北大学 山西省信息探测与处理重点实验室， 太原 030051；2.中北大学 信息与通信工程学院， 太原 030051)

1 引言

在舰船航行的过程中通过音频信号传递信息是不可或缺的，但舰船航行中各种设备产生的噪声会严重降低音频信号质量，影响工作人员或设备对音频信号的获取。因此降低音频信号中舰船噪声的干扰，增强音频信号质量对音频获取的准确性和舒适性具有重要意义。端点检测作为音频信号处理中必要的预处理环节，就是要在含噪信号中找到每段音频信号的首末位置，有效区分音频段与噪声段，为后续音频增强、识别等工作做好前期准备。

在舰载环境下，噪声类型多样，特征各不相同，并且设备工作时噪声巨大，使得信噪比较低[1]。而传统音频端点检测方法一般通过音频信号的统计特征与感知特征判断音频段与噪声段，例如基于短时能量和短时过零率的双门限法[2]、基于倒谱特征的检测算法[3]、谱减法与子带对数能熵积相结合的方法[4]等，此类算法在舰船背景噪声下会出现漏检、虚检率较高、鲁棒性低的问题。近些年基于机器学习的音频端点检测方法发展极为迅速，例如基于支持向量机[5]、BP神经网络[6]、卷积神经网络[7]的检测方法，当传统方法无法取得较好效果时，此类方法具有良好的区分性能，文献[6]研究表明，在15 dB粉红噪声环境下，双门限法准确率为85.37%，基于BP神经网络的算法准确率为93.88%。当信噪比为 0 dB时，双门限法已经无法得出稳定输出结果，而基于BP神经网络的方法准确率为89.32%。同时基于机器学习的方法可以更自然的与音频识别分类系统融合，但是较传统方法计算资源消耗大，且模型泛化能力通常比传统方法差[8]。

朴素贝叶斯算法是一种结构相对简单、参数较少的机器学习算法，相对于其他机器学习模型更容易实现。为了提高算法在舰载环境下端点检测的准确率，同时降低复杂性，提出一种多窗谱谱减法和朴素贝叶斯分类器相结合的音频端点检测算法。首先利用多窗谱谱减法对含噪信号进行处理以提高信噪比，然后将提取到的每帧信号特征输入分类器模型，最终判断出信号种类。仿真实验结果表明，相对于传统音频检测算法，本文中算法在舰船噪声环境下具有较高的端点检测准确率。

2 信号特征分析

噪声即发声体进行无规则振动时所发出的具有一定分贝的声音。舰载环境中的噪声源主要为舰船机舱设备，包括主机、发电机、锅炉等。舰船自身材料、发动机类型等也决定了其噪声特性,噪声特性的不同决定了对信号处理方案的不同。对舰船主要噪声做出以下分类：① 汽轮机声：舰船汽轮机工作因机械运转引起的振动和摩擦形成的噪音。② 海浪声：舰船行驶时海水拍打舰体的噪声。③ 枪炮声：作战时舰炮等武器开火时炮弹从炮筒内部发射出时内部气体振动及炮弹与空气摩擦产生的噪声。④ 人声：舰船内部人员之间的谈话声[9]。

在舰船中多种噪音混合叠加形成复杂的噪音，进而与音频信号进行重叠相加，无论音频信号是否存在，噪声一直存在。图1中上图为NOISEX-92数据集中驱逐舰机舱噪声波形，下图实线与点线分别为噪声信号与美国海军水面舰艇常规警报信号功率谱。驱逐舰机舱噪声能量主要集中在3 000 Hz以下的频段内，频段范围与人类语音信号500～3 500 Hz的频谱情形十分类似。常规警报信号在3 000 Hz以下频段内具有较高的能量分布，与噪声主要能量分布频段存在重叠。图2为美国海军水面舰艇另外3种警报信号的频谱分布特征，在3 000 Hz以下频段内也具有较高的能量分布。

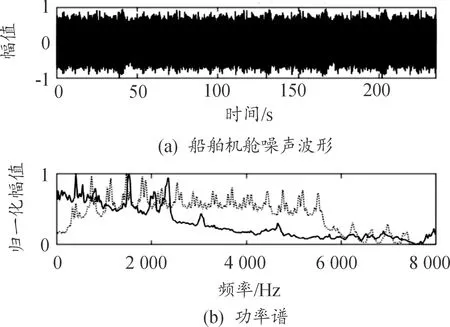
图1 噪声与常规警报功率谱

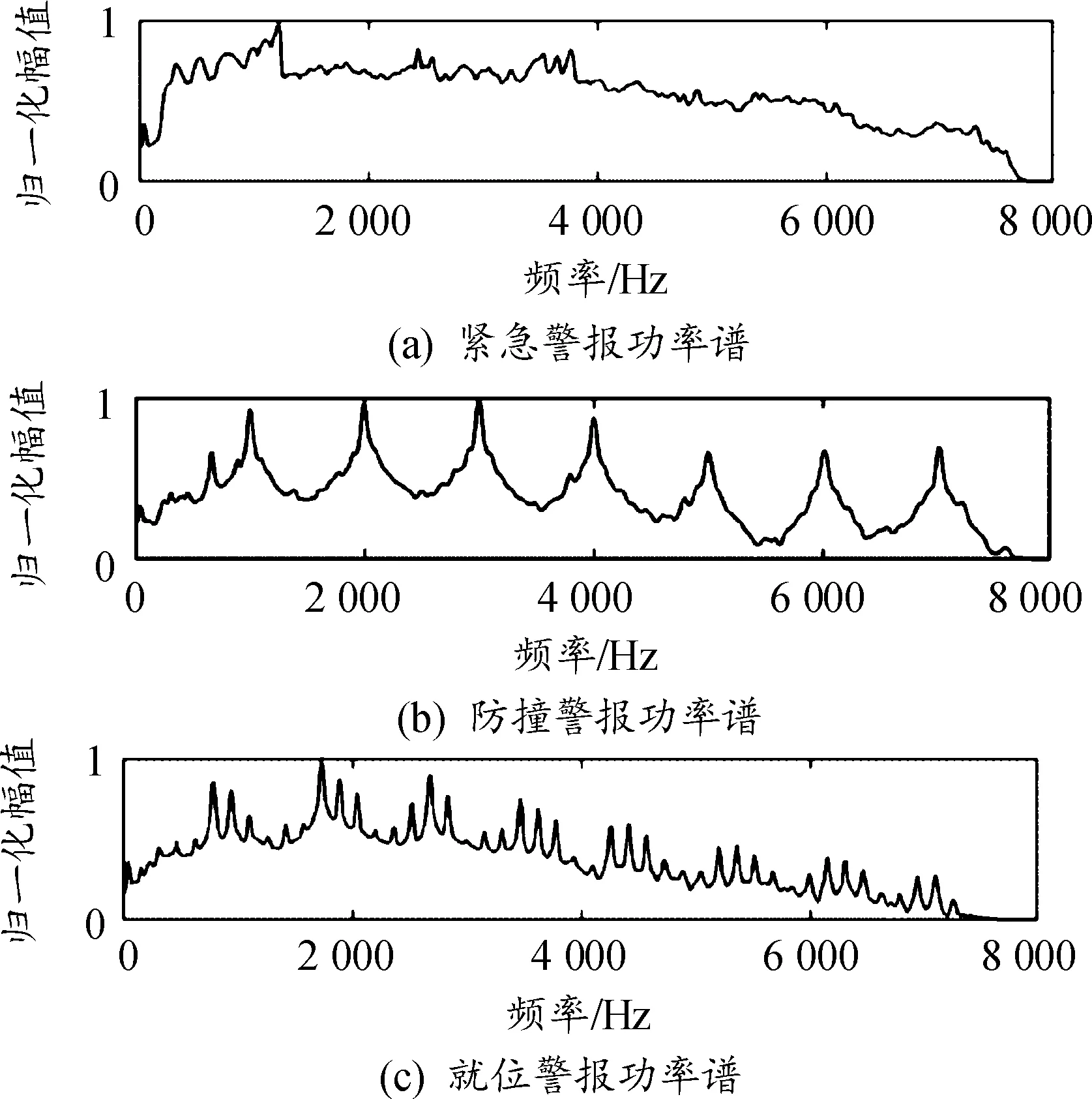
图2 警报功率谱

综上所述，噪声的混杂、噪声与音频信号频谱的重叠会使传统特征参数法在舰船噪声环境下的检测效果大幅降低，特别是在极低信噪比环境下，因此利用谱减法来初步提高含噪信号信噪比可以适当提高检测的准确率。

3 多窗谱谱减法

谱减法[10]是对纯净音频信号的功率谱或幅度谱进行估计重构的一种算法，其计算复杂度低且实时性强。多窗谱谱减法[11]由基本谱减法改进而来，通过使用多个正交窗分别求直接谱，然后对多个直接谱取平均值获取噪声谱值，计算过程如下：

(1)

(2)

式中：i代表第i帧；k代表第k条谱线。

计算噪声的平均功率谱密度值Pn(k)：

(3)

式中:l为前导无音频信号段帧数。

利用谱减关系计算增益因子：

(4)

式中：α为过减因子；β为增益补偿因子。α的取值直接影响到谱减的效果，采用固定α值一般不能得到最优的谱减效果。根据文献[4]的研究，结合舰船机舱环境需求，将增益补偿因子β固定为0.001，α随信噪比的最优变化模型为：

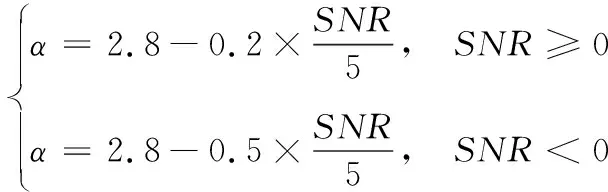
(5)

式中：SNR为含噪信号信噪比。

4 基于朴素贝叶斯分类器的端点检测算法

4.1 音频端点检测特征参数

分类算法检测音频端点效果的优劣与给定特征直接相关，单一特征对噪声的鲁棒性较差，使用多种特征或进行特征融合有利于发挥多类特征各自的优势，有效提高检测的准确率。

4.1.1MFCC0与GFCC0的融合特征

梅尔频率倒谱(mel-frequency cepstrum)是基于声音频率的非线性梅尔刻度的对数能量频谱的线性变换。梅尔频率倒谱系数(mel-frequency cepstralcoefficients，MFCC)就是组成梅尔频率倒谱的系数，因为其具有较好的抗噪性能和计算复杂度较低被广泛用在语音识别、音频分类[12]中。在统计实验中发现MFCC0在有声段上的值远远大于无声段上的值，因此可将MFCC0用于音频端点检测上。MFCC系数提取过程如图3所示。

图3 MFCC系数提取流程

具体步骤如下：

1) 对音频信号进行预加重、分帧与加窗等预处理。

2) 对预处理后的每帧音频信号进行FFT得到Xa(k)，利用该值可计算每帧音频信号的谱线能量Ea(k)：

Ea(k)=[Xa(k)]2

(6)

3) 将Ea(k)通过梅尔滤波器组，计算滤波器组输出的对数能量：

(7)

式中：m表示滤波器组中第m个滤波器；M为滤波器组中滤波器个数；Hm(k)为第m个滤波器的响应。

4) 输出的能量进行离散余弦变换得到MFCC系数：

(8)

式中：M(a,l)为第a帧音频信号的第l维MFCC系数。取每帧信号的第一维系数即为MFCC0特征，记为M(a)。图4为0 dB含噪信号谱减后的MFCC0特征。

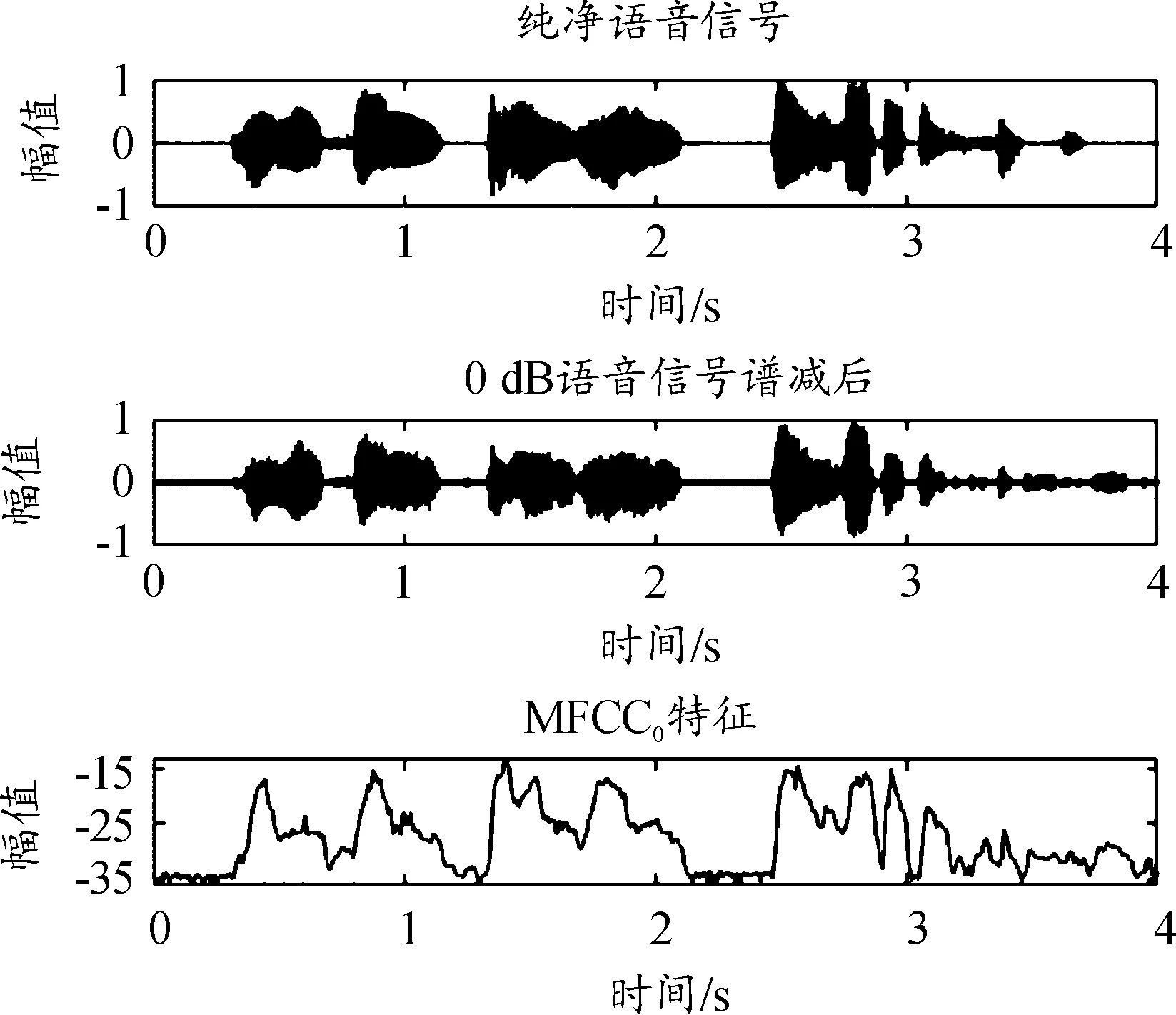
图4 信号MFCC0特征

经过研究发现，GFCC的第一维系数GFCC0相比于MFCC具有更强的噪声鲁棒性[13]。

与MFCC的提取类似，音频信号通过预处理和傅里叶变换后根据式(7)得到谱线能量Ea(k)，用Gammatone滤波器组进行滤波处理后进行指数压缩：

(9)

式中：m为滤波器组中第m个滤波器；M为滤波器组中滤波器个数；Hm(k)为第m个滤波器的响应；z为指数压缩的数值。将输出的能量经过离散余弦变换即可得到音频信号的GFCC系数：

(10)

式中：G(a,l)为第a帧音频信号的第l维MFCC系数。取每帧信号的第一维系数即为GFCC0特征，记为G(a)。图5为0 dB含噪信号谱减后的GFCC0特征。

图5 信号GFCC0特征

单一使用MFCC0或GFCC0会存在对音频段追踪能力不足的问题，对MFCC0和GFCC0进行融合可以有效解决这些问题，提高端点检测的准确率。图6为0 dB含噪信号谱减后的融合特征。

图6 信号融合特征

首先对得到的G(a)和M(a)进行中值滤波处理，然后对2组系数进行平移调整后取绝对值：

(11)

T(a)=G′(a)×M′(a)

(12)

4.1.2能熵比特征

文献[14]提出了一种新的对数能量特征，能够较好的反映信号中不同部分的区别，但在非稳定噪声环境下性能较差，而谱熵特征能够克服能量特征这一缺点，但其在嘈杂噪声中却变得不稳定。能熵比特征结合二者的优点，如图7所示。音频信号段的对数能量波形为上凸形状，谱熵值波形则相反，因此对数能量值除以谱熵值得到的能熵比[15]能够更加突出噪声段和音频段的差别。

图7 信号能熵比特征

能熵比计算过程如下：

计算第k帧信号对数能量：

(13)

式中：a为常数。设子带数为Nb，第i帧中第m条子带的能量为Eb(m,i)，子带能量概率pb(m,i)和子带谱熵计算式分别为：

(14)

(15)

能熵比表示为：

(16)

4.2 朴素贝叶斯分类器

朴素贝叶斯分类器在机器学习中是一种以假设特征之间强(朴素)独立下运用贝叶斯定理为基础的简单概率分类器。其原理如下：

设x={a1,a2,…,am}为一个待分类项，a为x的特征属性。C={y1,y2,…,yn}为类别集合。分别计算P(y1|x),P(y2|x),…,P(yn|x)，若其中最大值为P(yk|x)，则x∈yk。

其中，关键问题在于各个条件概率P(y1|x),P(y2|x),…,P(yn|x)的计算，可通过如下步骤求出：

1) 建立一个训练集，内容为一个已知分类的分类项集合。

2) 统计得到训练集中各类别下各特征的条件概率:

3) 假设特征之间是独立的，根据贝叶斯定理：

(17)

朴素贝叶斯算法逻辑简单易于实现，分类过程中时空开销较小，同时在很多情况下可以得到和相对复杂的分类模型相当的精度[16]。

4.3 基于朴素贝叶斯分类器的端点检测步骤

1) 准备阶段。以语音信号为例，选择一定长度的训练样本进行预处理后分帧，人工将语音帧与非语音帧分别标注为1，-1。然后提取每帧信号的特征值。

2) 训练阶段。这一阶段的任务是生成分类器，分别计算语音段和非语音段在样本中的出现频率及两个特征属性分别对语音段和分语音段的条件概率估计，并记录结果。

3) 应用阶段。含噪语音信号经多窗谱谱减法处理后提取每帧信号的特征作为分类器输入，分类器输出结果作为对每帧信号的检测结果。

5 实验仿真

5.1 实验设计

本实验在Windows操作系统实现,CPU为Intel 酷睿i5 8400,GPU为NVIDIA GTX 1060。仿真实验使用纯净语音信号与噪声信号相结合的方式验证算法，选用NOISEX-92数据集中的驱逐舰机舱噪声，音频信号从清华大学THCHS30数据库中选取，数据库中语音采样频率为16 kHz，采样位数为16 bit。使用Audacity软件读入语音样本，对每帧信号进行标注。在THCHS30数据库中抽取20条语音作为样本，在Matlab平台上对样本语音信号进行预处理及特征提取、完成分类器的训练。为验证算法在低信噪比噪声环境下的性能，随机抽取语音分别按照10、5、0、-5 dB的信噪比合成含噪语音信号。

音频信号具有非平稳性，为了在进行傅里叶变换时输入信号是平滑连续的，需要对信号分帧处理。通常认为音频信号在10～30 ms内具有短时平稳性，故分帧帧长取20 ms(320个采样点)，帧移10 ms(160个采样点)。

使用音频端点检测的正确率R作为算法评价标准，其定义为：

(18)

式中：L1为音频误判为噪音的帧数；L2为噪音误判为音频的帧数；L为信号总帧数。

5.2 实验结果与分析

从语音数据库中随机抽取10段语音与噪声信号叠加后分别使用常规谱减法[17]与多窗谱谱减法进行处理，分别计算信噪比后取平均值，结果见表1。

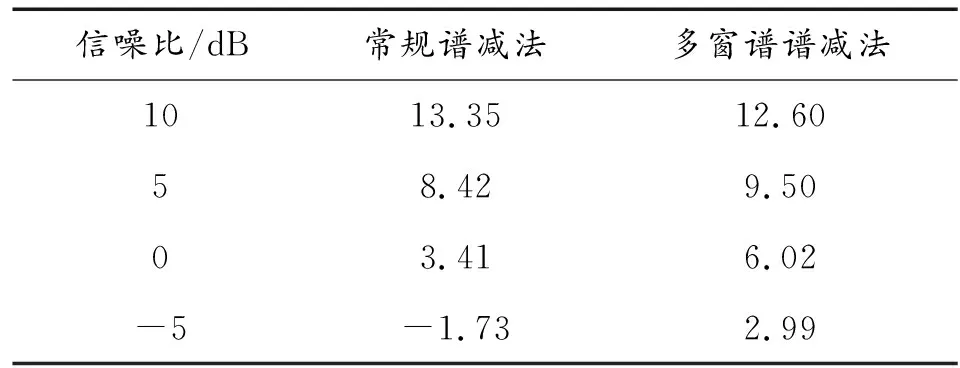
表1 2种谱减法后的平均信噪比(dB)Table 1 Average SNR after two spectrum subtraction(dB)

对比表1数据，常规谱减法在10 dB环境下的平均信噪比优于本文方法，但在5 dB及以下信噪比环境下本文方法优于常规谱减法，特别是在-5 dB极低信噪比环境下，多窗谱谱减法能够有效提高信号信噪比。0 dB信噪比环境下2种谱减法效果对比如图8所示。

图8 0 dB谱减法效果对比

选取传统算法中短时能量与过零率的双门限法和子带谱熵法[18]、多窗谱谱减法+SVM分类器与本文方法进行对比实验，并使用式(18)计算准确率，结果见表2。

对比表2数据，信噪比较高时几种端点检测方法均有较好的检测效果。随着信噪比的降低，2种传统方法的准确率骤跌，在0和-5 dB信噪比环境下的准确率已经低于实际应用的需求。而多窗谱+SVM分类器的方法与本文算法在相同环境下仍然有较高准确率，在10、5、0 dB环境下SVM分类器的检验正确率略低于本文算法，在-5 dB环境下朴素贝叶斯分类器的检测准确率相较于SVM分类器提高了约11%，表现出更强的抗噪性。

表2 不同信噪比端点检测准确率(%)Table 2 Detection accuracy of endpoints with different SNR

图9—图11分别为双门限法、子带谱熵法与本文算法在0 dB驱逐舰机舱噪声环境下的检测结果。

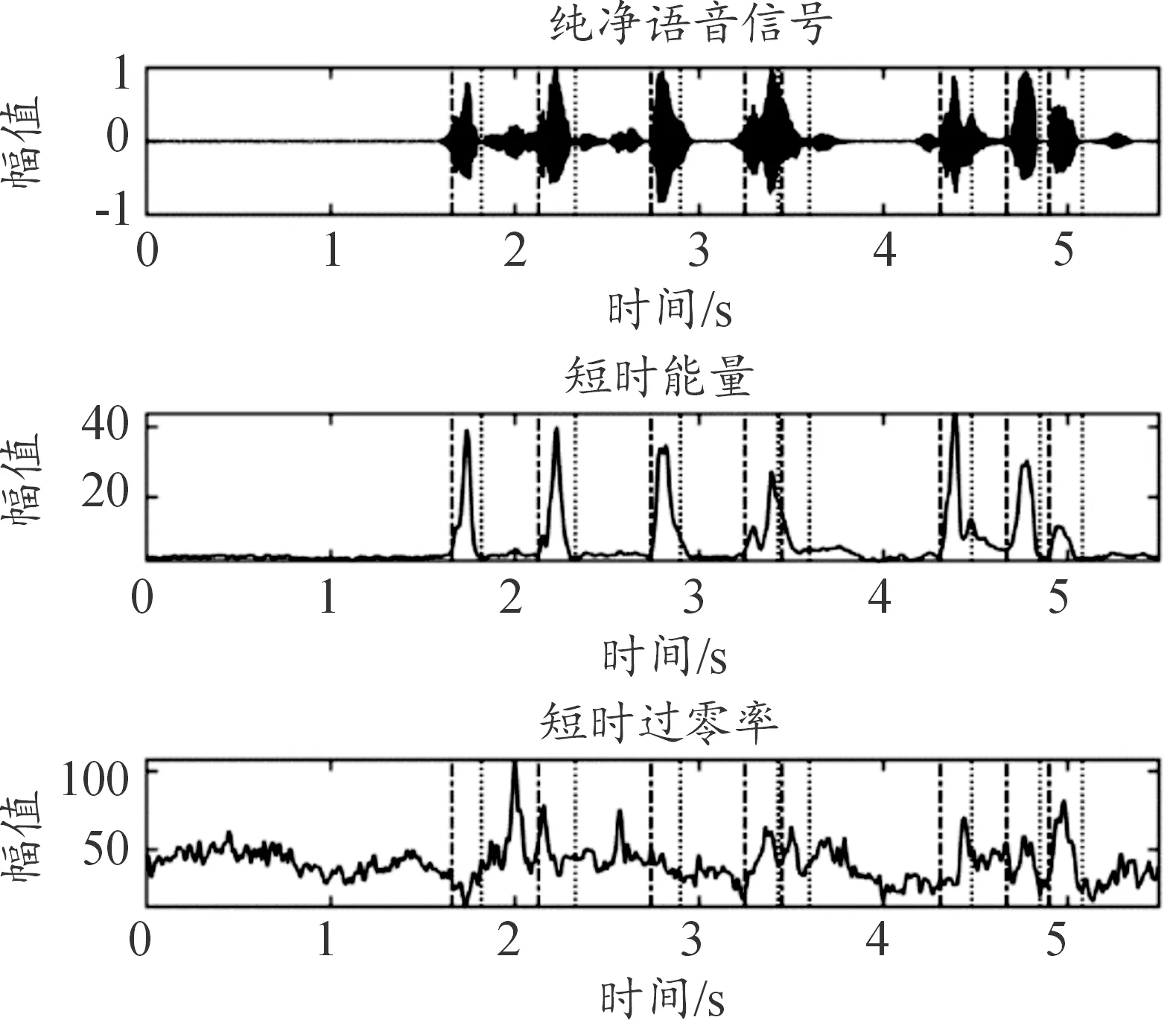
图9 0 dB环境下双门限法检测结果

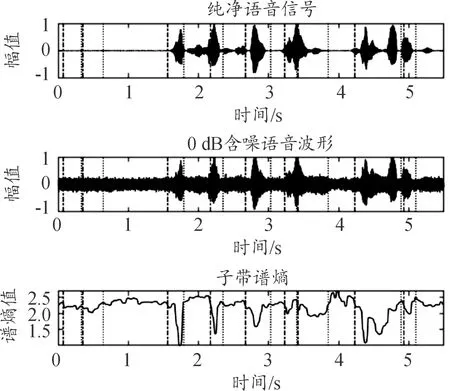
图10 0 dB环境下子带谱熵法检测结果

图11 0 dB环境下本文算法检测结果

计算复杂度是衡量算法性能的重要指标，设训练样本数为n，特征数为f，分类类别为c，支持向量数量为s，则朴素贝叶斯的训练时间复杂度为O(nfc)，预测时间复杂度为O(fc)，支持向量机的训练时间复杂度为O(n2)～O(n3)，预测时间复杂度为O(f)到O(fs)。本次仿真实验中2种算法训练时间与预测速度见表3，对比可得朴素贝叶斯分类器模型的训练时间与预测速度均优于SVM分类器模型。因此采用本文算法进行音频端点检测可以获得较满意的结果。

表3 2种分类器复杂度对比Table 3 Comparison of the complexity of two classifiers

6 结论

针对舰船复杂噪声环境下音频端点检测准确率及鲁棒性较低的问题，提出了一种谱减法和朴素贝叶斯分类器相结合的音频端点检测算法。主要结论如下：

1)利用多窗谱谱减法对含噪信号进行处理，提高了含噪信号信噪比，为在舰船复杂噪声环境下音频端点检测的准确率的提高奠定基础。

2)使用融合特征作为分类器的输入，发挥了多类特征各自的优势，提高了音频端点检测的准确率。

3)本文所使用的朴素贝叶斯分类器算法逻辑简单易实现，仿真结果表明，在驱逐舰机舱噪声环境下得到了较高的检测准确率，具有良好的检测效果。