空间站宏微机械臂动力学建模与零反作用控制

尹旺 王翔 王为 刘冬雨

(北京空间飞行器总体设计部，北京 100094)

空间站舱外机械臂系统一般由大型柔性机械臂和固连在其末端的刚性灵活机械臂组成。如国际空间站上的加拿大2臂和专用灵巧手、日本实验舱的遥控机械臂系统(JEMRMS)和中国空间站上的核心舱机械臂和实验舱小臂[1]。宏机械臂用于实现大范围转移运动，微机械臂用于实现精细化操作。采用行星齿轮减速器的宏机械臂会表现出大挠度的特点，如果不采取措施，微机械臂运动时会在惯性力的作用下激起宏机械臂末端的大幅度振动，从而影响微机械臂末端的精度和效率。另外，为提高机械臂的灵活性和可操作性，微机械臂通常具有一定的冗余自由度，因此此类宏微机械臂最主要的特点是支撑结构的柔性和自由度的冗余性。

抑制柔性基座机械臂弹性振动的方法主要有被动控制方法和主动控制方法。被动控制方法是通过选用各种耗能材料及对机械结构进行优化设计，从而达到降低柔性结构弹性变形、控制结构振动的目的[2]。主动控制方法是通过外部能量的输入以获得期望的阻尼、刚度特性，从而抑制柔性结构的动态响应。主动控制主要有前馈控制(输入整形[3]、轨迹规划[4])和反馈控制[5]两种典型方法，前者应用时只需要建立系统的动力学模型而不用测量基座振动量的传感器设备，在工程中的应用时简单可靠，但是前馈控制的调节时间长、鲁棒性较差，当系统模型存在误差时不再适用。反馈控制是根据系统振动状态的反馈信息来产生作动力/力矩，从而实现柔性机械臂的轨迹跟踪和振动控制。

诸多学者利用冗余机械臂的自运动能力进行了抑振研究。文献[6]基于拉格朗日乘子法和最小二乘推导得到冗余机械臂的反作用最优控制，并从理论上证明了两种控制方法的一致性，试验证实所提方法能减微机械臂运动产生的反作用力矩。文献[7]等人指出由于系统中柔性坐标远多于机械臂的冗余度，基于上述方法求得的只是最小二乘意义上的反作用最优解，故提出一种新的算法，该算法利用机械臂冗余特性可消除在模态空间的低阶模态力，因而具有更好的抑振效果。同时，国内的文献[8]也对自运动优化选择的复模态法进行了研究。文献[9]将反作用零空间的思想应用到柔性基座机械臂中，并提出一种综合控制律，该控制律充分利用逆动力学模型，能同时满足柔性基座的振动抑制、反作用激振最小以及末端轨迹跟踪等任务。文献[10]将JEMRMS/小精细臂(SFA)系统的前三个关节视为柔性关节，后九个关节视为微机械臂，并将文献[9]提出的综合控制算法成功应用到该系统，仿真结果证实了这种综合控制算法对于真实的宏微机械臂系统是有效的。

文献[10]等并没有将柔性宏机械臂等效为柔性基座，为了获取更多的冗余自由度，将宏机械臂的部分关节与微机械臂关节同时控制，这在实际应用时难度较大。为了满足空间站宏微机械臂分时独立控制的任务需求，本文首先将宏机械臂等效为柔性基座，并对微机械臂进行了零反作用运动控制，使得微机械臂在完成任务的同时不对基座产生任何扰动。

1 柔性基座机械臂系统建模

1.1 问题描述

空间站建造完成进入运营阶段后，空间机械臂主要用于舱外载荷照料、在轨可更换单元替换以及航天员转移等，微机械臂末端是相对于空间站运动的，因此在运动学关系上空间机械臂相当于地面机械臂。另外，空间站自身质量远大于机械臂系统，机械臂运动对站的姿态影响很小，因此本文将宏机械臂基座坐标系xIyIzI视为惯性参考系，宏臂和微臂末端的固连坐标系分别为xMyMzM，xeyeze，两者的运动都是相对于xIyIzI而言的，如图1所示。

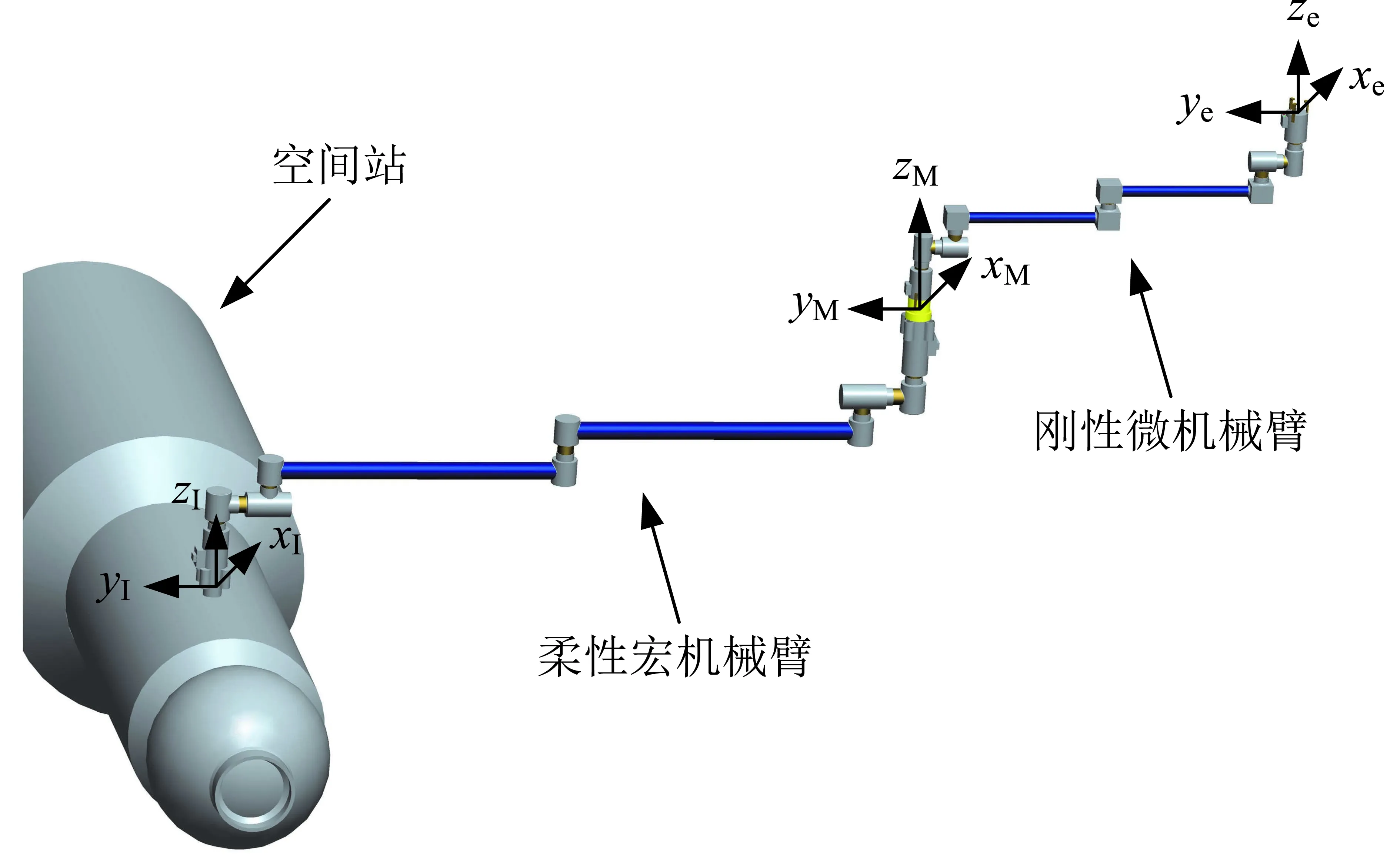
图1 空间站宏微机械臂示意图Fig.1 Macro-micro manipulator mounted on space station

地面实验表明，由碳纤维增强基复合材料制作而成的臂杆刚度远大于关节刚度，宏机械臂的柔性主要来源于柔性关节[11]，因而本文不考虑宏机械臂臂杆柔性的影响。

1.2 柔性基座机械臂运动方程

柔性关节宏机械臂的动力学模型为

(1)

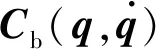
文献[12]中和[13]中分别给出了宏机械臂末端的惯量特性和等效刚度矩阵为

(2)

(3)

式中：JM为宏机械臂末端在固定基下的雅克比矩阵。由此可见，宏机械臂末端的惯量特性和刚度矩阵随其构型的变化而变化，当宏机械臂处于某一固定构型时，A(q)和Ke(q)可近似为常值矩阵。此时柔性宏机械臂等效为六自由度柔性基座与空间站相连，根据拉格朗日方程可求得柔性基座的受迫振动方程为

(4)

式中：xb∈R6×1为柔性基座的位姿矢量；Fb(t)为柔性基座受到的广义外力。

刚性微机械臂的动力学方程为

(5)

式中：Hm为微臂的惯性矩阵；Cm为微臂的哥氏力和离心力；τm为微臂的驱动力矩。式(4)和式(5)分别给出了刚性微机械臂与柔性基座的动力学模型，两个子系统有着各自的动力学特性，当结合在一起后会相互影响。由于两者之间存在动力学耦合作用，因此柔性基座机械臂系统不是柔性基座和刚性机械臂之间的简单结合，而是通过耦合项将两者耦合在一起的。根据拉格朗日方程和牛顿—欧拉法推导得出柔性基座机械臂的动力学方程为

(6)

2 零反作用运动控制

当微机械臂自由度大于柔性基座的自由度时，微机械臂具有反作用零空间，即微机械臂在运动过程中各连杆产生的反作用力相互抵消，从而不对柔性基座产生任何扰动，从而实现微机械臂与基座之间的运动解耦。微机械臂的零反作用运动控制可基于关节加速度的控制律实现。

(7)

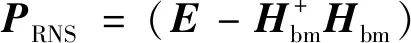
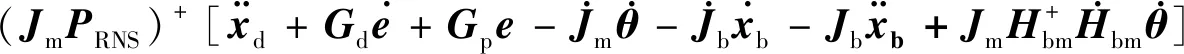
(8)

式中：Jm和Jb分别为微机械臂和柔性基座的雅克比矩阵；xd是期望的跟踪路径；e=(xd-x)为路径的跟踪误差；Gd和Gp为合适的增益矩阵。式(8)代入式(7)即可得到基于加速度的零反作用轨迹跟踪控制律。该控制律应用的前提是微机械臂自由度大于柔性基座自由度，另外惯性耦合矩阵应该行满秩，否则会发生动力学奇异。

3 仿真分析

3.1 等效模型验证

由图1知，宏机械臂具有7个自由度，等效为柔性基座后具有6个自由度(3个平动，3个转动)，为表明等效前后动力学特性不变，首先分析两者的固有频率。宏机械臂肘部关节(关节4)连接的两臂杆跨度最大，因而对宏机械臂末端的动力学特性最大，其他连杆跨度较小，影响较小。为分析宏机械臂肘关节对柔性系统各阶固有频率的影响，设宏臂构型为q=[0,0,-30,θ4,90,90,0]°，其中θ4在-180°～+180°之间变化。计算结果如图2所示，红色虚线代表柔性宏机械臂固有频率，蓝色实线为柔性基座固有频率。

7自由度的柔性宏机械臂等效为6自由度的柔性基座，会丢失1阶固有频率。由图2(e)知当肘关节小于-60°时，柔性基座和柔性宏机械臂的第5阶固有频率对应相同，相当于丢失了第6阶频率；当肘关节大于-60°时，柔性基座的第5阶固有频率与宏机械臂的第6阶相同，相当于丢失了第5阶频率。由于柔性宏机械臂的5、6阶固有频率相差很小且远大于基频，因此，宏机械臂等效为柔性基座后丢失的1阶固有频率对动力学特性的影响很小。

由图2(c)和(d)可知，等效柔性基座模型与机械臂3、4阶频率相差稍大，原因在于当肘部关节位于0°和180°附近时，宏机械臂雅克比矩阵的最小奇异值较小，即宏机械臂接近奇异构型，此时进行动力学等效时会造成一定误差。但出现误差的频率都在3 rad/s以上，而基频在1 rad/s以下，因此该误差对整体的动力学特性影响也可接受。

从图2(a)发现柔性宏机械臂的基频随着肘关节角的变化而变化，当肘关节角度为±180°时基频最高，当肘关节角度为0°时基频最低，表明宏机械臂折叠程度越高，基频越高，等效成的柔性基座稳定性越好；伸展程度越高，基频越低，柔性基座稳定性越差。

为验证所建立模型的正确性，采用ADAMS商业软件进行仿真对比。宏机械臂初始时刻处于静止状态，关节锁定时角度为q=[0,0,-30,-60,90,90,0]°，假设宏机械臂柔性关节刚度为100 Nm/(°)，ADAMS提取的固有频率和基于模型的计算结果如表1所示。刚性微机械臂进行空间点到点的运动，初始时刻关节角度为θ0=[0,0,-90,0,90,0,0]°，终止时刻构型为θf=[90,-90,-90,120,90,0,0]°，仿真时长为10 s，采样周期为0.02 s，各关节角位移采用五次多项式的轨迹，起止时刻的关节角速度、角加速度均为零，如图3所示。对于柔性基座而言，激励载荷即为微机械臂各关节的角位移，如图4所示，柔性基座的振动响应如图5所示。

图3 柔性宏刚性微机械臂仿真模型Fig.3 Simulation model of flexible macro-rigid micro manipulator

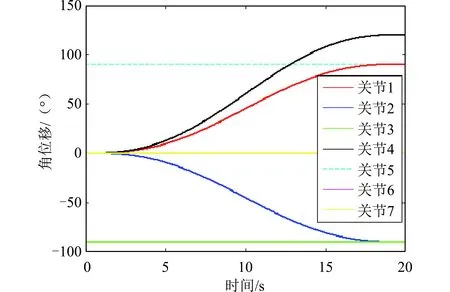
图4 微机械臂关节角位移Fig.4 Joint angle of micro manipulator

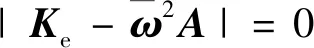
表1 柔性宏机械臂及柔性基座各阶固有频率Table 1 Natural frequencies of flexible macro manipulator and flexible base rad/s

从仿真曲线可以看出柔性基座振动位移曲线完全吻合，分析结果说明了本文给出的柔性基座机械臂动力学建模的正确性和合理性。给出的动力学方程可作为空间站宏微机械臂级联控制的基础模型。

3.2 零反作用运动控制

假设宏机械臂处于完全伸展构型，即q=[0,0,-90,0,90,0,0]°，此时宏机械臂为奇异构型，考虑到各关节的弹性变形沿轴线方向，则宏机械臂末端具有3个柔性自由度，即宏臂末端只能在沿着x轴、绕着y轴和绕z轴的方向发生弹性位移。

微机械臂具有7自由度，此时柔性基座机械臂的反作用零空间是4维的，不考虑姿态的变化，基于式(7)和式(8)所示的控制律，微机械臂末端可跟踪三维空间内任意轨迹而不引起基座的振动。假设微机械臂初始构型为θ0=[0,-90,-60,60,135,60,0]°，末端沿着直线从(1.6，-2.4，-3.1)运动到(1.0，-1.8，-2.5)，该坐标是末端固连系xeyeze相对于惯性系xMyMzM的描述，过程中微机械臂对柔性基座的反作用及弹性位移如图6所示。

图6 柔性基座振动位移及其反作用Fig.6 Vibration deformations and reaction of the flexible base

由图6知，对机械臂采用零反作用的轨迹跟踪控制时，基座在3个柔性自由度方向所受的反作用力/力矩均为零，因此微机械臂能在完全不激起基座扰动的前提下完成轨迹跟踪任务，图7给出了微机械臂在不同视角下的运动轨迹。

图7 基于零反作用的末端轨迹跟踪控制Fig.7 Trace of end-effector based on reaction null-space control

4 结束语

本文将柔性关节宏机械臂等效为柔性基座，经数值仿真证实两者动力学特性的一致性。基于该简化模型能方便地得到柔性宏机械臂在各种构型下的固有频率，宏机械臂伸展程度越高，固有频率越低，反之。将零反作用轨迹跟踪法成功应用于真实结构的柔性基座机械臂的运动控制中，使得微机械臂在不引起基座扰动的前提下完成轨迹跟踪任务，为我国空间宏微机械臂在轨级联操作提供了借鉴意义。本文中的仿真是以大臂位于奇异构型为例进行的零反作用控制，因为奇异构型下的大臂柔性自由度减少，柔性基座机械臂的反作用零空间维度相应增大，因而小臂在完全不引起基座扰动的前提下能完成更高维度的轨迹跟踪任务。对于大臂其它非奇异的构型，可采用模态截断技术略去柔性基座的高频响应，利用文中方法可完全消除小臂在运动过程中激起的低频振动，从而实现基座的抑振控制，提高组合臂末端操作稳定性。