波纹腹板几何参数对轴压比的影响
2023-04-03曹会敏余浩铭刘洪兵
曹会敏,余浩铭,刘洪兵
(1.西北工业大学,陕西 西安 710072;2.西安交通工程学院,陕西 西安 710300)
0 引言
波纹腹板钢是一种在一定条件下相较于普通H 型钢构件受力更优越且更加节省钢材的新型钢材,近年来受到广大科研工作者的关注[1-2]。国内在建筑领域关于波纹腹板钢的研究多集中在力学性能如抗剪、抗弯、疲劳、稳定性等方面,而动力学性能的研究多集中在桥梁领域如孙鹏辉[3]利用ABAQUS 有限元软件研究腹板倾斜角度对主梁动力特性的影响规律。戚伟利[4]采用大型通用有限元软件Midas/Civil 建立模型,通过设置不同位置及不同数量横系梁进行动力特性分析。冯文章[5]根据箱梁截面抗剪能力相等原则,建立了波纹钢腹板连续刚构桥和相应的混凝土腹板连续刚构桥有限元模型,对二者的动力特性和抗震性能进行了对比分析。基于此,笔者与其他研究人员从2016 年展开了对波纹钢在建筑领域动力特性的研究,并于2018 年发表了波纹腹板H 型钢框架结构动力特性分析[6],通过对比波纹腹板钢结构和普通钢结构的动力特性及分析地震波作用下两种结构的反应特点发现波纹腹板钢框架结构的刚度与抗震性能都优于普通H 型钢。由于构件的动力性能与构件的轴压比密切相关,本文将继续研究波纹腹板H 型钢构件几何参数对轴压比的影响,为后期此类构件在动力特性方面的进一步研究提供理论依据。
1 模型及假定
1.1 模型创建
模型基于ABAQUS软件创建,采用C3D8R实体单元,钢材本构模型见图1,材料参数见表1,图2 腹板波折参数示意图,表2 为构件参数对照。模型构件一端施加荷载一端完全固定,加载方式见图3 与图6。
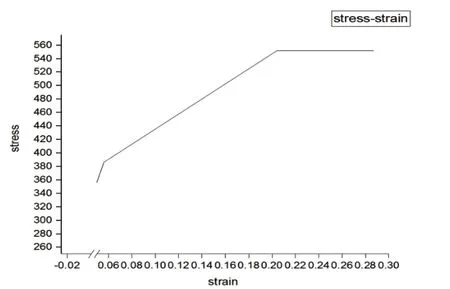
图1 材料本构模型
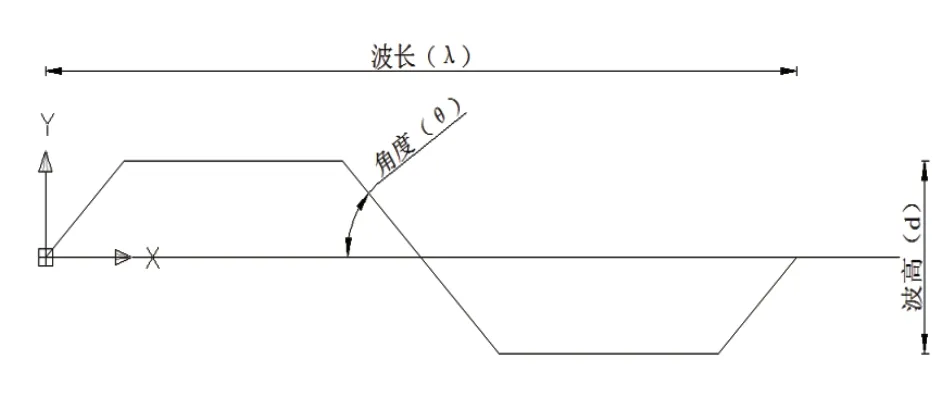
图2 腹板波折参数
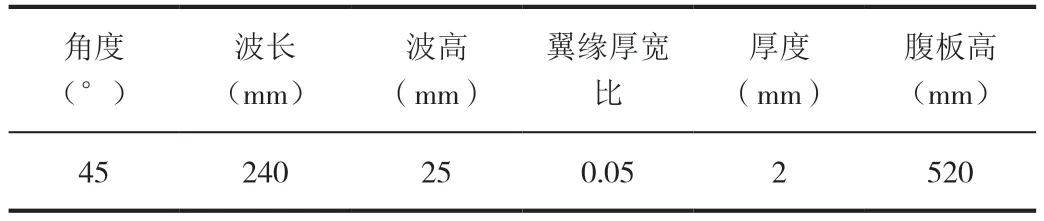
表1 材料参数

表2 构件几何参数对照表
1.2 计算假定
由于波纹腹板构件在轴压力作用下翼缘承担了几乎所有的力,而腹板基本不起作用,因此本文轴压比计算假定抗剪满足要求,不考虑腹板发挥的作用,利用n=计算,其中N 为轴向压力值,Af为翼缘净面积,f 为钢材抗拉强度设计值。
2 荷载作用下轴压比对构件的影响
在讨论几何参数对轴压比的影响前,先来观察结构在不同轴压比时结构的破坏特点与规律,以下给出了构件在不同轴压比时的破坏云图、荷载位移曲线和应力应变曲线。
2.1 轴压荷载作用
由于轴压力作用时,若荷载直接加载在腹板上可能会导致局部应力集中使变形较大,因此,将梁的两端封闭起来作为刚性加载板如图所示,加载方式如图3 所示。

图3 轴心荷载加载图
由表3 可知,波纹腹板H 型钢构件两翼缘的应力随着轴压比的增加逐渐增加,直到构件达到强度极限值而无法再承担荷载的增加时破坏。此时腹板应力值的增加较为缓慢,直到翼缘出现塑性铰发生破坏时腹板的应力值依然很小,说明在轴压比达到某一值之前构件的腹板不会破坏。由PEEQ 云图可以看出,构件腹板与翼缘连接处的应变值偏大,与Mises 应力图结论基本一致,构件的破坏主要是翼缘和翼缘与腹板的连接点附近的破坏。

表3 各轴压比作用下构件的破坏形式
当轴压比为0.8 时材料单元开始屈服,但未达到构件的破坏应变0.204。随着轴力的增加塑性区逐渐增大,当轴压比在1.6与2 之间的某个值时构件发生破坏。此变化过程中,腹板与翼缘接触附近区域破坏较严重。
由图4 荷载位移曲线可知:荷载达到1 388kN 附近时,荷载位移曲线是一条直线,因此可知1 388kN 附近的某个值是该构件的弹性极值点,此时近似认为1 388kN 为构件的弹性极值点。图5 得出的应力应变曲线完整地反映了构件整个破坏过程,该曲线符合一般应力应变曲线的变化规律。弹性段为符合胡克定律的直线段,由各轴压比值对应得出的弹性极限值求平均值可得到弹性极限值约为1 313.557kN,此时弹性极值点对应的轴压比为1.059。因此,轴心压力作用时,构件的轴压比值已超过了1。此时荷载位移曲线弹性极值点对应的轴压比n=1.12。两种曲线得出的轴压比值相差很小,说明荷载位移曲线与应力应变曲线得出的结论一致。
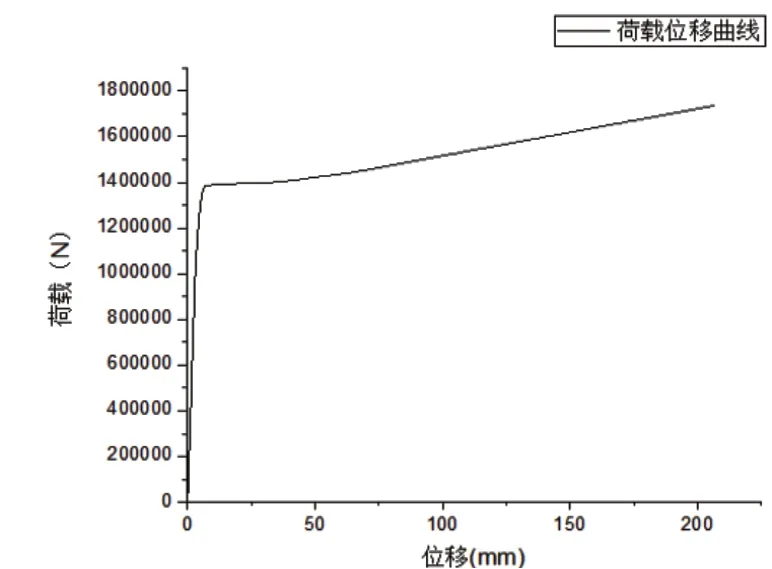
图4 荷载位移曲线
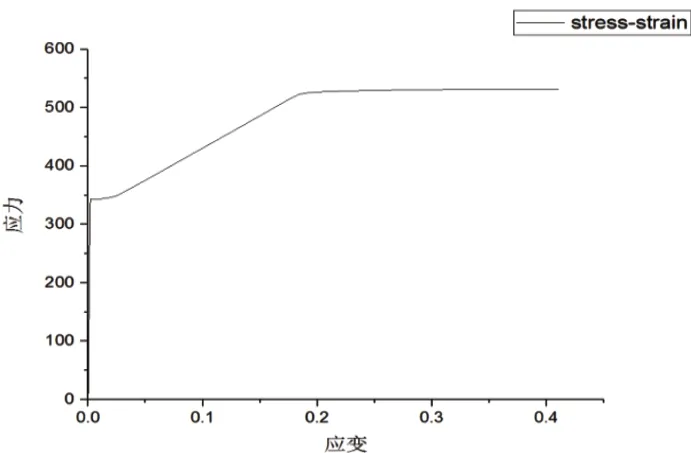
图5 应力应变曲线
2.2 偏压荷载作用
由轴压荷载作用分析可知,轴压作用下荷载的弹性极值约为1 313kN。经过大量分析可知,当结构构件受偏压荷载1 300kN 时可出现结构破坏的整个过程,因此构件施加此荷载便可得到本节研究所需的数据。加载方式如图6 所示。

图6 偏心荷载加载图
此处设:a=偏心距/腹板高度
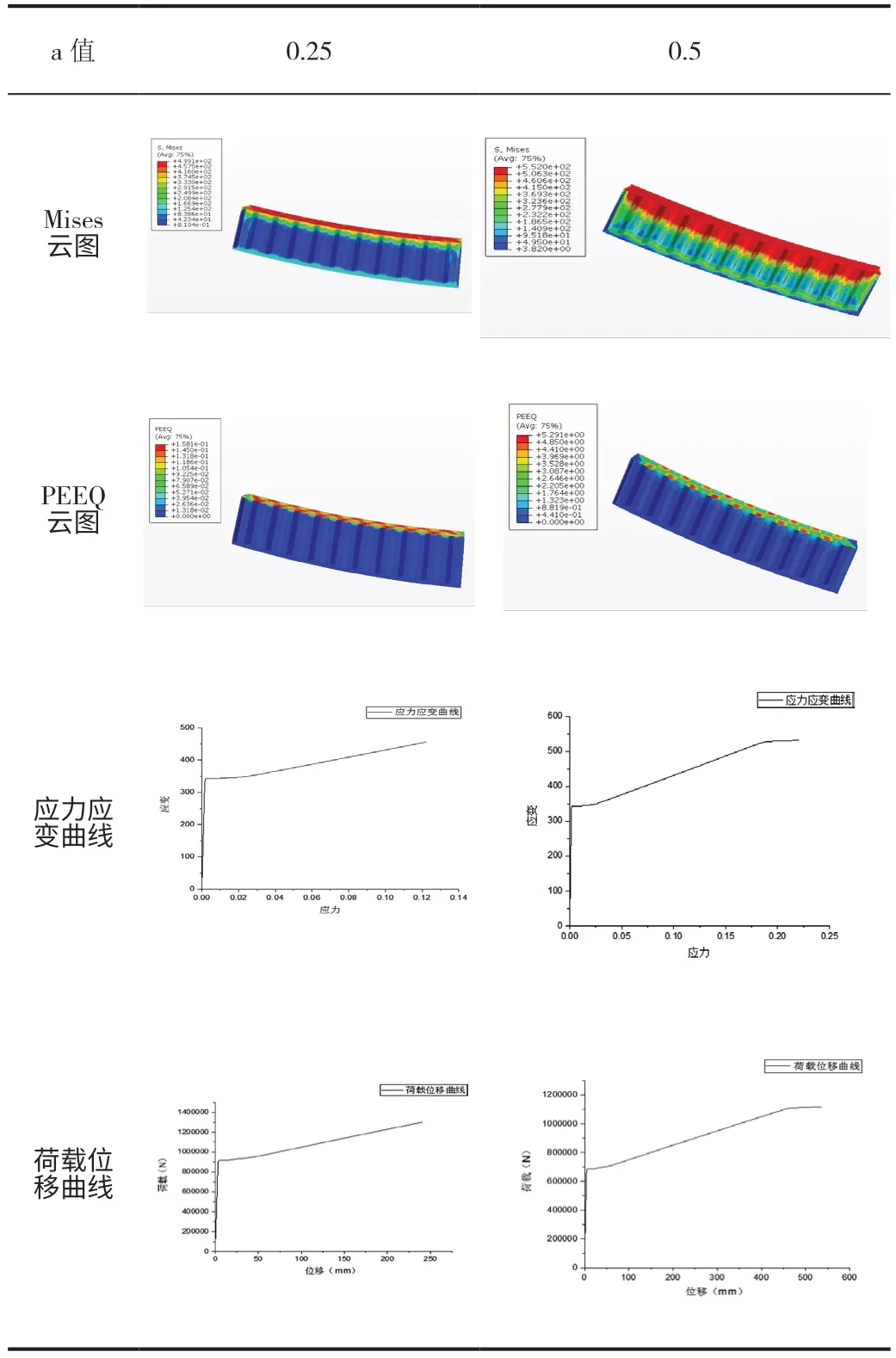
表4 偏心荷载作用下构件的破坏
通过比较a=0.25 与a=0.5 时构件的Mises 云图、PEEQ云图与位移云图可得,结构构件在荷载作用位置不同时的破坏特点基本一致。首先是离荷载较近一侧的翼缘应力值急剧增加,随后另一侧翼缘的应力也开始增加,随着荷载不断增加,离荷载较近一侧的翼缘首先破坏,紧接着腹板也逐渐不能承受荷载的增加而破坏,但此时离荷载较远一侧翼缘的应力反倒不再增加。说明此时构件已不能再承受荷载的作用。
当a=0.25 时,由荷载位移曲线与应力应变曲线可得,构件的弹性极限承载力值约为872kN,此时对应的轴压比n1=0.703。当a=0.5 时,同样的偏心力值作用下构件的应力应变曲线已达到了强度极限值,由荷载位移曲线与应力应变曲线可得,构件的弹性极值约为635.748kN,此时对应的轴压比n2=0.5127。
3 波纹腹板几何参数对构件轴压比的影响规律
利用控制变量法,对照表2 分别改变构件的波折角度、波长、波高、翼缘宽厚比、腹板厚度来观察构件轴压比的变化规律。
3.1 波折角度的影响
基于表2,保持其他参数不变,通过改变构件的波折角度来观察轴压比的变化情况,角度取值分别为22.64°、30°、45°、60°、75°、90°。
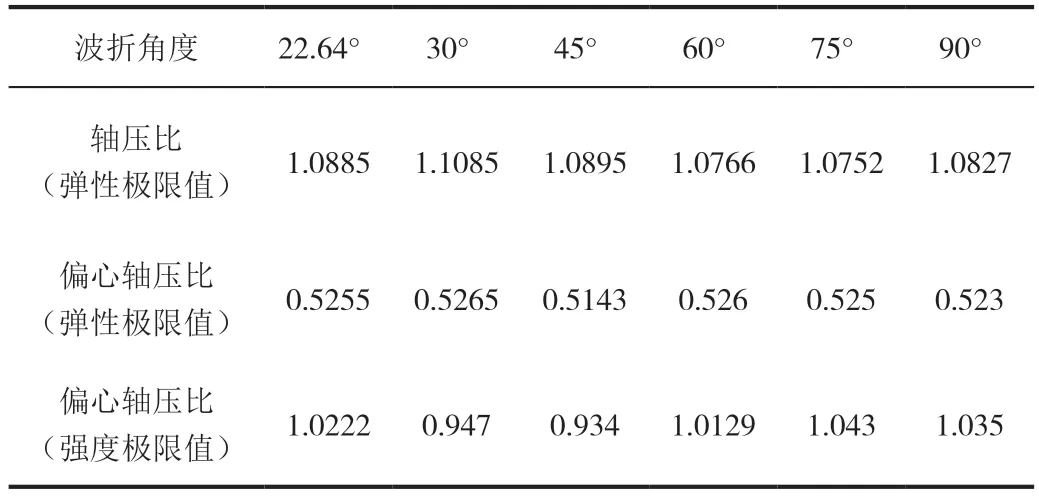
表5 波折角度对轴压比的影响
3.2 波长的影响
基于表1,保持其他参数不变,通过改变构件的波长来观察构件轴压比的变化情况,波长值分别为150mm、180mm、210mm、240mm、270mm、300mm。
3.3 波高的影响
基于表2,保持其他参数不变,通过改变构件的波高来观察构件轴压比的变化情况,构件波高值分别为10mm、20mm、30mm、40mm、50mm、60mm。
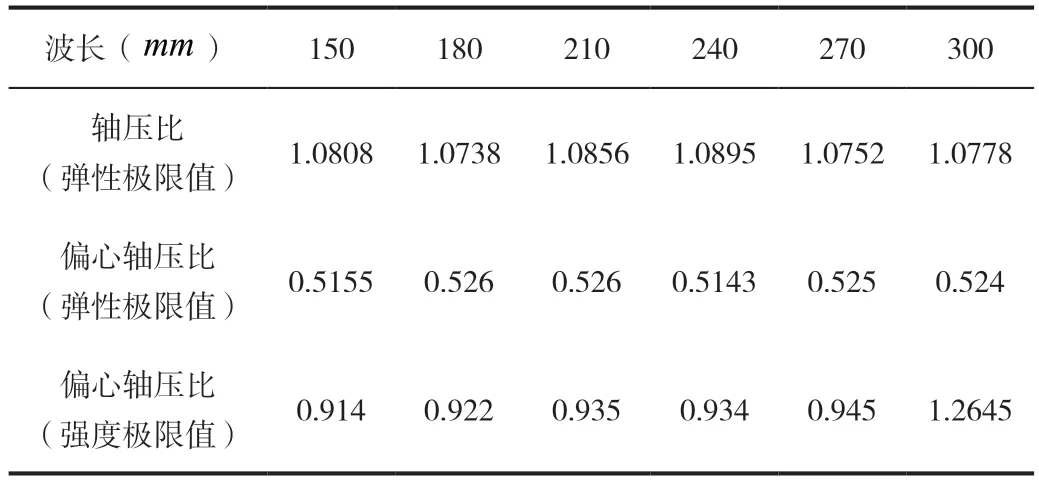
表6 波长对轴压比的影响
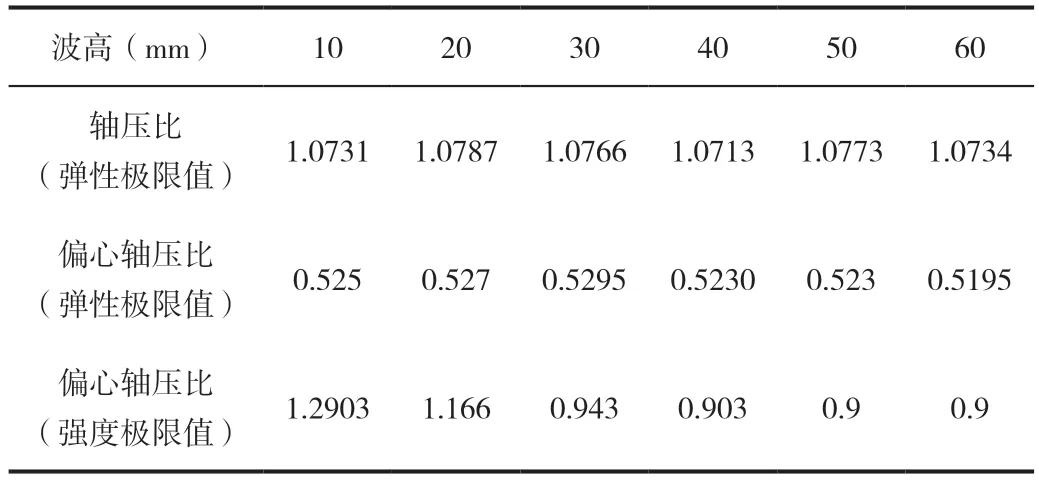
表7 波高对轴压比的影响
3.4 腹板厚度的影响
基于表2,保持其他参数不变,通过改变构件的腹板厚度来观察构件的轴压比变化情况,构件腹板厚度值分别为2mm、3mm、4mm、5mm。
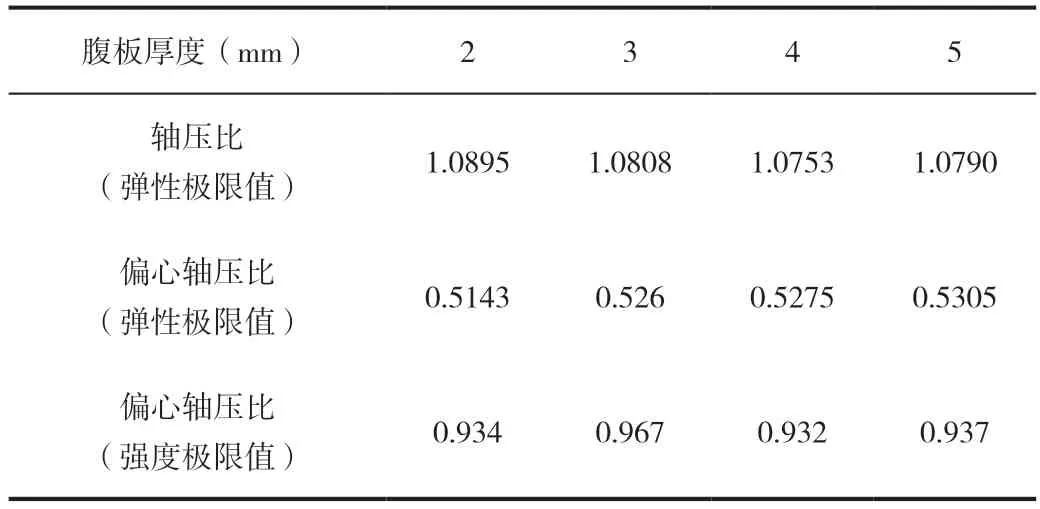
表8 腹板厚度对轴压比的影响
3.5 翼缘尺寸的影响
基于表2,保持其他参数不变,通过改变构件的翼宽比来观察构件的轴压比变化情况,翼缘厚宽比分别为0.025、0.05、0.075、0.1。
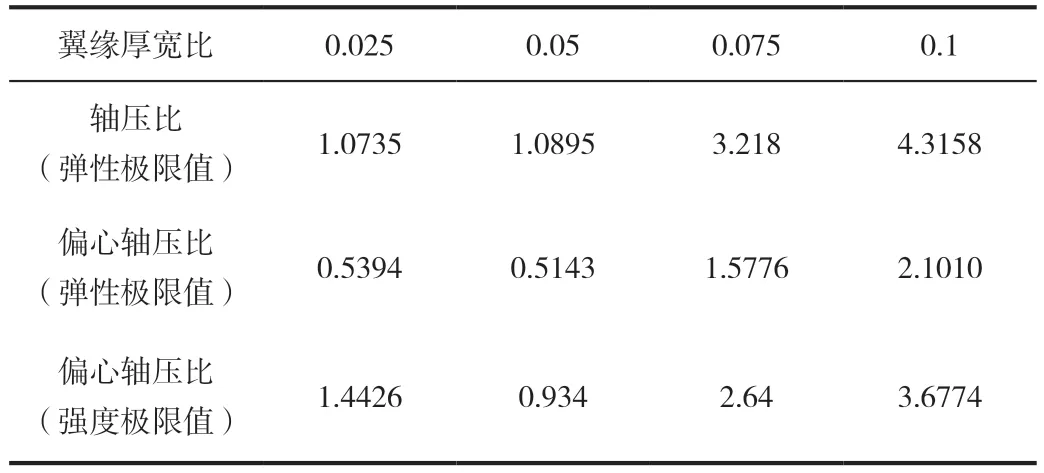
表9 翼缘宽厚比对轴压比的影响
4 结论
(1)波纹腹板H 型钢构件波长的变化仅会影响构件在偏心荷载作用下的强度极限值,波长太大时会使构件的延性变差;
(2)构件的延性随波高的增加而增加;
(3)波纹腹板H 型钢构件的腹板厚度对轴压的影响较小;
(4)翼缘尺寸对构件的轴压比值的影响较大;
(5)若将构件控制在弹性阶段则轴压比值可以0.51 为限值,但若以强度破坏作为构件破坏的控制标准,则轴压比的值要视构件的各项几何参数综合而定。
