航空发动机涡轮流场仿真与涡轮功计算

徐学文， 盛 沛， 陈黎明

(海军航空大学, 山东 烟台 264001)

航空发动机涡轮是燃气膨胀做功带动压气机及附件旋转的核心部件，涡轮性能是影响发动机功率、效率的关键因素[1-3]。其中，标度涡轮做功大小的主要指标之一涡轮功是指每千克燃气在涡轮中膨胀后在涡轮轴上实际输出的功，是涡轮的有效功。如果不考虑轮盘的摩擦损失和机械损失，涡轮功等于每千克燃气对涡轮(转子)所做的功——轮缘功；如果考虑轮盘的摩擦损失和机械损失，涡轮功小于轮缘功。当前对航空发动机涡轮功的计算通常采用热力分析法[4-5]，即根据涡轮进口燃气总温和涡轮出口燃气总温，计算出燃气在涡轮中等熵膨胀条件下的焓降值，再乘以涡轮效率，得出涡轮实际输出功率。这种结果完全从热力学角度分析得出，未考虑涡轮转速、几何结构特点和受力特性，无法进一步开展涡轮特性分析[6]。

本文从力学角度[7-8]出发，首先通过计算机仿真技术计算出导向器-涡轮叶片周边流场参数分布，通过有限体积法计算出涡轮叶片上圆周力，由此推导出每千克燃气在单位时间内对涡轮所做的功——轮缘功，再根据涡轮效率计算出涡轮功。这种方法为进一步开展航空发动机涡轮特性分析提供了更方便、更经济的途径。

1 仿真计算模型

1.1 流场模型

本文仿真计算的某型航空发动机涡轮为单级轴向涡轮。从燃烧室出来的高温高压燃气首先经过导向器叶栅通道高速膨胀，在出口处获得足够速度后，直接冲击在涡轮转子叶片上，推动涡轮旋转做功，并在流经涡轮叶栅通道过程中持续做功。涡轮带动压气机等部件旋转。燃气在涡轮叶栅通道流动过程中，速度、压力与温度不断变化。涡轮叶片沿轴向受力变化比较大，而沿径向受力变化比较小。为简化计算，假设叶片沿径向受力均匀一致，选取导向器、涡轮各一叶片作为研究对象，建立导向器-涡轮二维流场仿真模型，如图1所示。

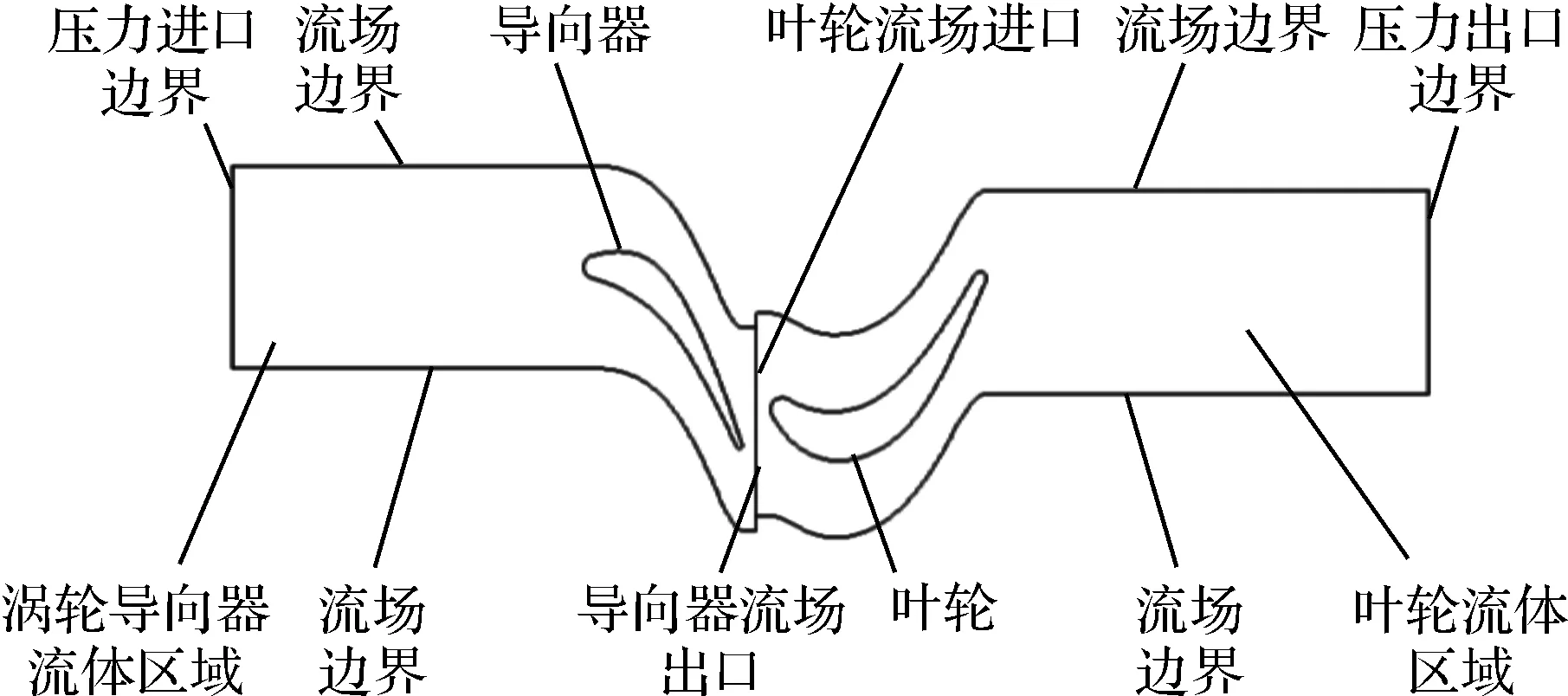
图1 航空发动机涡轮二维流场仿真模型

1.2 计算方程

流场仿真控制方程[9]采用二维可压粘性方程。

质量守恒方程：

(1)

动量守恒方程：

(2)

能量守恒方程：

(3)

式中：ρ、ui、p、E和xi分别是流体的密度、速度分量、压力、能量和Eulerian坐标分量；t为时间；qi为热流量；τij是切应力分量。

湍流模型采用计算精度比较高且应用比较广泛的k-ε二方程模型。

k控制方程：

(4)

ε控制方程：

(5)

另外，为使方程组封闭，这里采用完全气体状态方程：

p=ρRT

(6)

1.3 边界条件

本文选取发动机在地面冷态运转时稳定转速410 r/min进行仿真计算，仿真模型边界条件[10]如图1所示。

(1) 进口边界条件

(2) 出口边界条件

(3) 叶片壁面条件

假设气体与涡轮叶栅通道壁面之间均为“无滑移”条件，壁面粗糙度为常数0.5。

(4) 转子-静子界面条件

在导向器出口与涡轮进口之间采用转子-静子间滑动边界条件，即在转子流场区域与静子流场区域的边界重合区域定义为内部区域，边界上其他区域(非重合区域)为周期区域。转子与静子间滑动速度为Vst=29.445 m/s。

涡轮中气体流动守恒就是从转子与静子间重叠区域界面计算得到。

(5) 周期边界条件

不管是导向器还是涡轮，其上叶片均为均匀分布，因此这里选取各自一个叶片及其周边流场区域作为仿真模型，在叶片周边流场两侧边界设定为周期边界。

2 流场仿真结果

本文采用有限体积法[11]的无结构化网格离散导向器-涡轮叶片周边流场区域[12]，流场网格如图2所示，网格单元数为7 917，最小单元面积为6.554×10-4m2，最大单元面积为2.709×10-2m2。

图2 流场仿真网格

仿真过程分两步：第一步，设定滑动边界条件的滑动速度为0，用二阶迎风格式耦合算法求解流场控制方程，得到流场稳态仿真结果，作为第二步瞬态流场仿真的初始化值；第二步，启动转子-静子间滑动边界条件，采用二阶隐式耦合算法计算瞬态流场控制方程，时间步长为0.000 1 s，计算时间为 0.1 s。

在计算迭代过程中，文中除了监控流场主要变量的收敛性外，还监控了涡轮叶片升力系数随时间步长变化情况，如图3所示。在仿真过程中(1 000个时间步长)，转子叶片经历15个力高-低峰变化周期，也就是转子15次叶栅通道变化周期，从变化曲线看出，流场在第12个变化周期后趋于周期性稳定，计算结果收敛。

从图4中看出，涡轮运转至不同位置(不同时间)，叶片壁面受力分布不一样，并且叶盆上面的压力比叶背上高得多，压力分布如图中所示。在涡轮叶片一个变化周期内(通过一个导向器叶栅通道)，叶片上压力与粘性摩擦力的合力的分力——圆周力Fu变化如图5所示，它推动涡轮叶片高速旋转。

图4 涡轮壁面(叶盆和叶背)上压力分布

图5 涡轮上圆周力一个周期内变化曲线

3 涡轮功计算

气体在流经涡轮叶栅通道过程中，单位时间内燃气对涡轮所做的功为：

Lu=Fu×u

(7)

式中：u为叶片圆半径为r的切向线速度，u=ω×r。

在涡轮叶片一个变化周期T内，燃气对涡轮所做的平均功为：

(8)

每千克燃气单位时间内对整个涡轮叶片(n个叶片)所做的功——轮缘功为：

(9)

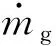
根据式(9)计算出该型航空发动机在地面冷态运转时稳定转速为410 r/min下轮缘功为lu=47.2 kW/kg。

4 结论

(1) 从力学角度出发，通过流场仿真计算出涡轮流场参数分布，通过有限体积法计算出涡轮叶片上圆周力，由此推导出每千克燃气单位时间内对涡轮所做的功，流场仿真精度直接决定了涡轮功的计算精度，如果在流场仿真中考虑摩擦损失和传热损失等，将大大提高涡轮功计算精度。

(2) 文中推导的涡轮做功的计算公式，不仅与燃气流场参数有关，还与涡轮转速、叶片几何结构有关，该公式更适合于涡轮特性分析与结构设计。