基于直觉模糊贝叶斯网络的HUD 系统多阶段任务可靠性分析

张帆，孙紫荆，肖国松，刘嘉琛，王鹏，*

1．民航航空器适航审定技术重点实验室，天津 300300

2．中国民航大学 安全科学与工程学院，天津 300300

平视显示器（Head Up Display，HUD）是一项航行新技术，能够将飞行所需数据信息集成显示在飞行员前方显示面板上，使飞行员能够以平视状态获取必要飞行及导引信息，及时修正飞行状态，实现精细化飞行［1］。中国民航局《平视显示器应用发展路线图》提出，未来我国主要干线航空飞机制造商，对其新设计的机型均需提供HUD 安装选项，其中部分制造商要将HUD 设备作为标准配置［1］。

目前，中国自主研发的国产HUD 系统尚在起步阶段，部分关键模块及元器件缺乏服役经验、可靠性数据积累不足，难以为可靠性分析提供可信的底层数据支撑，存在亟待解决的认知不确定性问题。此外，HUD 系统在工作中存在多阶段运行特点，各工作阶段系统构成存在差异而元件状态相互关联。同时可能存在的共因失效问题及其相关的概率数据模糊，也使得可靠性分析中的不确定问题愈加严重，作为可靠性分析领域的典型问题，忽视共因失效可能造成最终的分析结果的较大偏差。

在底层可靠性数据缺失问题方面，模糊理论是处理系统认知不确定性的有效方法，在解决概率数据不完全、不确定等问题上成果显著。模糊理论在应用中多与专家启发式技术相结合，用于专家意见的聚合，能够有效处理专家共识不足或意见偏颇带来的不确定性问题。文献［2］将模糊理论与故障树分析相结合的模糊故障树分析（Fuzzy Fault Tree Analysis， FFTA）方法应用于风险评估分析技术，文献［3］将FFTA 方法应用于储油罐失效概率分析，文献［4］对FFTA 方法进一步扩展改进，用于评估储油罐火灾风险，文献［5］将模糊集的概念扩展到直觉模糊集，提出了一种基于直觉FFTA 的方法，并将其应用于油罐系统部件的失效评估。

而在多阶段任务系统的可靠性模型建立及共因失效的表征问题上，基于概率论与图论的贝叶斯网络（Bayesian Network， BN）在事件逻辑关系描述与概率推理方面具有更大优势，在安全风险分析与可靠性分析领域应用广泛［3，6-9］。在贝叶斯网络与模糊理论的交叉研究方面，文献［10］将模糊贝叶斯网络纳入人为因素分析框架，处理事故中人为错误和组织失误的相互依赖性、不确定性和数据不足等问题，文献［11］提出基于模糊贝叶斯方法的不确定环境下易燃液体罐车实时风险分析。文献［12］利用考虑专家权重的方法对模糊数进行综合，进一步进行BN 计算得到瓦斯泄漏发生概率。基于以往研究，模糊贝叶斯网络在可靠性分析领域有很强的适用性，而在HUD 系统可靠性分析中还未得到应用。

以模糊理论支撑HUD 系统多阶段任务可靠性分析的过程，关键即是以模糊理论对系统多阶段任务的贝叶斯网络模型的输入数据进行处理的过程。依据前述研究，这一过程需要经过专家语义评价、评价模糊化、模糊聚合、解模糊处理等步骤。在语义评价阶段，对于复杂系统，评价人员往往无法直接给出模糊对象的隶属度进行直接准确的评估，即专家评价本身也存在不确定，而前述研究工作很少将专家评价本身的准确性纳入考虑。在模糊数聚合阶段，多重模糊数据处理存在不确定性积累问题，即聚合后模糊数的区间范围大于最初定义的模糊区间，模糊累积会降低最终解模糊结果的准确性。在解模糊处理阶段，需要将聚合所得的直觉模糊数转换为具体的失效数值，文献［13］提出的转换方法已经在多个行业中有诸多应用［14-17］，但考虑到不同行业、不同类型设备的概率空间分级标准不同，该方法无法适用于各种模糊数的转化，采用不适当的模糊区间可能导致计算结果与实际情况有明显的偏差。

针对专家评价准确性问题，直觉模糊理论作为模糊集的拓展，包括隶属度、非隶属度和犹豫度的模糊概念，能够更好地表达专家意见的模糊性和不确定性［18］。对于多重模糊数据处理中不确定累积问题，文献［19］在FFTA 模型中引入了Tω 算子，用于天然气运输船机械推进系统的可靠性评估。文献［20］将基于Tω 的模糊算法进行扩展，提出了直觉模糊故障树分析（Intuitionistic Fuzzy Fault Tree Analysis， IFFTA）方法，并将该方法应用于某武器系统可靠性评估。依据前述研究，提出将Tω 算子引入模糊贝叶斯网络的分析，以减少模糊性积累带来的计算偏差。而在模糊数转化方面，结合民机领域适航当局与工业界普遍接收的定性概率术语，提出更适用于航电设备的模糊区间分级与转化算法。

综上，针对国产HUD 系统可靠性数据积累不足、难以为可靠性分析提供底层数据支撑的问题，提出基于直觉模糊贝叶斯网络的航电设备多阶段任务可靠性分析方法，并将可能出现的共因失效纳入考虑，能够实现系统基本事件概率数据模糊与共因事件概率数据模糊条件下的可靠性分析。

1 基本理论

HUD 系统的可靠性分析工作存在2 方面关键问题，即系统多阶段任务的表征与底层可靠性数据确定。系统任务表征方面，需要构建能够反映系统多阶段运行行为以及可能出现的共因失效影响的综合贝叶斯网络模型。而在可靠性数据确定方面，对于数据模糊的底层事件，依据直觉模糊理论进行模糊数据确定，以Tω 算子降低模糊累积影响。

1.1 贝叶斯网络

贝叶斯网络（Bayesian Networks， BN）是以概率论和图论为基础的不确定推理模型，包括有向无环图及相应的条件概率关系。一个n节点的贝叶斯网络表示为，其中，E为网络各节点之间的有向边，Ω={X1，X2，…，Xn}为网络中的变量，则即表示具有n个节点的有向无环网络结构；P为与网络中节点所对应的条件概率分布（Conditional Probabilities Distribution，CPD）或条件概率表（Conditional Probabilities Table，CPT）。

对于网络中的节点Xi与Xj，有向边由Xj指向Xi则节点Xi为Xj的子节点、节点Xj为Xi的父节点。没有父节点的节点称为根节点，没有子节点的节点称为叶节点。以pa（Xi）表示Xi的父节点集合，以A（Xi）表示Xi的非后代节点集合，若给定pa（Xi），则Xi与A（Xi）条件独立，即

则基于贝叶斯网络的条件独立性，条件概率分布可以表示为P{Xi|pa(Xi)}。设定网络中各节点对应的CPD 或CPT，即可得所有网络节点的联合概率分布：

贝叶斯网络推理已有诸多成熟算法进行概率推理与最大后验概率解释［21-26］，在构建系统贝叶斯网络模型后可以依据网络节点联合概率分布计算系统可靠度：

1.2 多阶段任务系统

多阶段任务系统（Phased-Mission System，PMS）包含多个不重叠子阶段，系统在各个子阶段中依次执行指定任务。在不同阶段中，系统配置形式、失效标准等可能不同。在后续研究中，PMS 系统遵循以下基本假设：① 系统遵循二态假设，即系统与组成元件都只有“正常”与“失效”2 种状态；② 元件失效不可修复，一旦某元件在运行中失效，则在后续任务中都不可用；③ 系统各阶段间具有连续性，元件在某一阶段开始时的状态与上一阶段结束时状态相同；④ 系统各阶段间的切换过程不存在失效；⑤ 所有阶段任务成功则认为系统整体任务成功。

1.3 直觉模糊理论

直觉模糊集（Intuitionistic Fuzzy Set，IFS）理论是传统模糊集理论的扩展，相比传统模糊集理论，IFS 理论考虑了模糊数隶属度、非隶属度以及犹豫度，直觉模糊集即表示为一个三元有序集。

式 中：：X→[0，1]与νA͂：X→[0，1]分 别为隶 属度与非隶属度。满足：

(x)∈定义为x∈的直觉模糊指标，即x对的犹豫度，表示为

式中：0 ＜(x)＜1，∀x∈X。实数R 的IFS 如图1 所示，(x)为凸模糊曲线，上半连续，而(x)为凹模糊曲线，下半连续。当x取x0时，(x0)即为x0对A的犹豫度。当(x)=0，IFS 即为传统的模糊集。

图1 实数R 的IFSFig. 1 IFS of R

作为最常用的三角模糊数的扩展，三角直觉模糊数（Triangular Intuitionistic Fuzzy Set，TIFS）表示为=(a，b，c；a'，b'，c')，其隶属度函数与非隶属度函数如下：

1.4 基于Tω 的模糊集运算

Tω 范数是T 范数的经典形式之一，它能够减少模糊性的积累，是不确定情况下复杂系统评价算法中常用的算子。

对 于2 个TIFN，=(a1，b1，c1；a'1，b'1，c'1)和=(a2，b2，c2；a'2，b'2，c'2)，其基本运算规则如表1所示，其中λ为系数。

表1 基于Tω 的2 个TIFN 运算规则Table 1 Two TIFN operation rules based on Tω

2 基于直觉模糊贝叶斯网络的多阶段任务系统可靠性分析模型

提出基于直觉模糊贝叶斯网络（Intuitionistic Fuzzy Bayesian Networks，TIBN）的可靠性分析方法，包括3 大步骤，即贝叶斯网络模型构建、对模糊可靠性支撑数据的处理、基于贝叶斯网络的可靠性分析，分析流程如图2 所示。

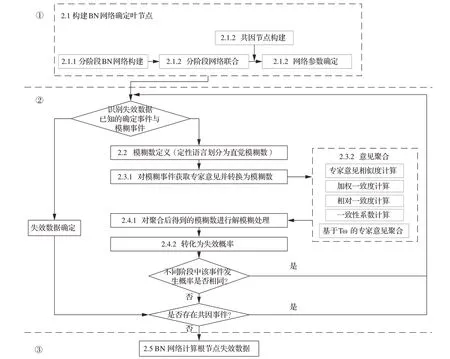
图2 基于TIBN 的可靠性分析方法Fig. 2 Reliability analysis method based on TIBN

首先依据待分析系统及其任务，建立多阶段任务系统的贝叶斯网络模型，明确网络中的叶节点。其次依据所提基于直觉模糊理论的分析方法对系统中难以判定失效数据的模糊节点进行分析，其中包括对失效数据模糊的系统元件以及共因失效事件的定量数据估计。最后依据贝叶斯网络推理算法对系统任务可靠性进行计算。

2.1 考虑共因失效的多阶段任务系统贝叶斯网络模型构建

2.1.1 多阶段任务系统贝叶斯网络模型构建

多阶段任务系统的贝叶斯网络模型由不同阶段各自的分阶段模型整合而成。各阶段中系统的贝叶斯网络模型构建与常见的不考虑阶段划分的系统BN 模型构建过程相同，首先需对系统组成以及运行中各元件/模块的逻辑关系进行分析，划分元件、组件、模块、子系统、系统等不同层级，确定合理的分析粒度以及各层级的网络节点，而后以有向边对各层级节点进行连结。此外，如某一层级中存在节点间因果或依赖关系，也应根据BN 网络构建规则进行连结。

在得到各运行阶段的BN 网络模型后，依据运行次序对各BN 模型进行整合，形成PMS-BN 模型。当某一元件/模块在不止一个运行阶段中发挥作用，该元件节点在整合的BN 模型中不能合并，仍应以不同的节点表示。而后以有向边顺次连结在不同阶段中重复出现的元件对应的各个节点。

需要注意的是，以有向边连结重复出现的元件对应的节点，是仅对所有根节点而言的，对于中间层节点，即使某一模块或子系统对应的节点在不同阶段中都出现，也不需要将其与上一阶段该模块节点直接连接。

2.1.2 共因失效事件模型

在PMS-BN 模型基础上，考虑共因失效问题对模型进行扩展，形成PCCF-PMS（Probabilistic Common Cause Failure-Phased Mission System）模型。首先构建共因空间节点，将其作为所有可能受到共因事件影响的元件节点的父节点引入网络中，即网络结构的扩展。其次对共因空间节点及可能受到共因事件影响的元件节点进行条件概率关系的更新，即网络参数修正。

1）共因空间节点构建

构建一个多状态节点CCE（Common CauseEk）表征所有可能出现的共因事件，包含各个共因事件发生或不发生的不同组合状态。若系统运行中可能受n个共因事件CCi（i=0， 1， 2，…，n）的影响，则共因空间包含2n个子空间且互不相交，记为CCEk（k=0，1，…，2n-1）。则：

将CCE 节点引入网络中，所有可能受到共因事件影响的元件节点均由PMS-BN 网络中的根节点变为CCE 节点的子节点。

2）网络参数更新

系统运行中可能出现的多个共因事件之间可能存在独立、互斥、相关等不同统计关系，因此在CCE 节点的CPT 参数确定时需要考虑其不同的统计关系。

对于各个共因事件的不同关系，CCE 节点的发生概率如表2 所示。对于CCi=1，有集合S=

表2 CCE 节点概率分布Table 2 Probability distribution of CCE

在可能受共因事件影响的元件节点CPT 确定方面，计算某一元件的总条件失效概率。

若在共因空间CCEk下，阶段j中元件X被m个共因事件（CCj1（X），CCj2（X），…，CCjm（X））影响，则元件X在阶段j之前都未失效的条件下，在阶段j中失效的总条件概率QjkX为

式中：qjX为元件X在j中的独立失效概率；qjiX为在阶段j中影响元件X的第i个共因事件发生的条件下，元件X的条件失效概率，也可记为qX|CCji(X)。

若某共因事件CCji（X）发生将使得元件X必然失效，则该共因事件为确定型共因事件，令qjiX=

2.2 定性评价的模糊化

专家以定性的语言描述对数据模糊的网络叶节点的失效可能性进行评估，因此需要将定性评价转化为［0，1］内的失效模糊区间，即直觉模糊失效数（Intuitionistic Fuzzy Failure Number， IFFN）。定性评价越接近0，即意味着该节点失效可能性越小，反之，越接近1，即该节点越可能失效。

文献［27］对人类记忆能力进行了普遍估计，即人类做出适当判断所需的语言表达的正确数量在5～9 个之间［9，28］。在民机适航领域，当使用定性或定量的分析判断对CCAR 25.1309 条款［29］的符合性时，一般被工程接受的概率术语如表3 所示［30］。因此，综合考虑民机适航当局与工业界普遍接收的概率术语，以及专家语言评级区间划分数量的合理性，将失效可能性语言术语定义为5 个级别，分别为 “可能失效”“失效可能较小”“失效可能微小”“失效可能极微小”“极不可能失效”，如表4 所示。

表3 民机系统及设备常用失效概率术语Table 3 Commonly used terms of failure probability for civil aircraft systems and equipment

表4 失效可能性定性分级Table 4 Qualitative classification of failure possibility

采用三角直觉模糊数，依据定义的5 个定性语言分级，以归纳推理方法量化相应的失效可能性数值［5，31-32］，如图3 所示，则失效可能性定性语言与IFFN 对应关系如表5 所示。

表5 失效可能性与IFFN 对应Table 5 Failure probability corresponding to IFFN

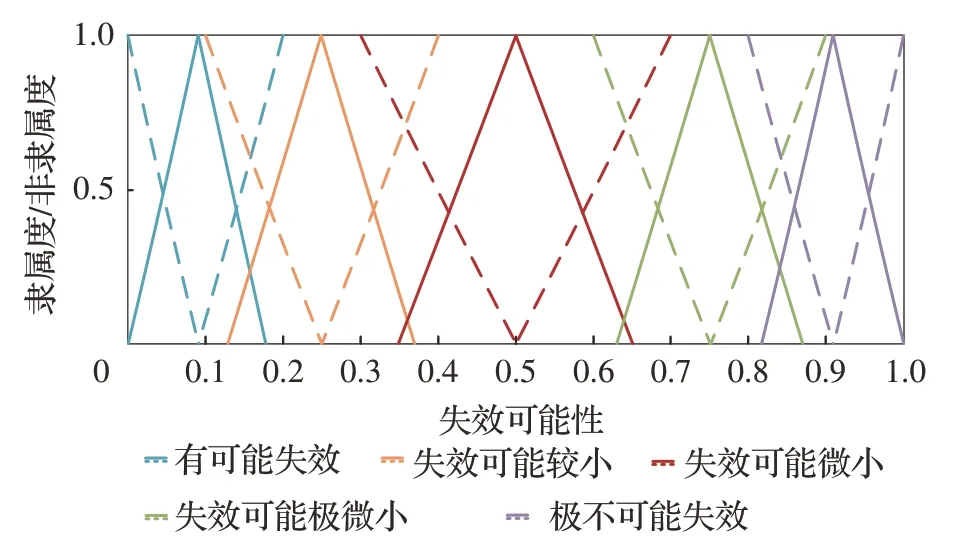
图3 定性评价的量化Fig. 3 Quantification of qualitative evaluation

2.3 专家评价与意见聚合

2.3.1 专家评价

基于贝叶斯网络的定量可靠性分析依赖根节点先验概率与节点CPT，当根节点先验失效率数据缺乏时，通常需要借助专家的知识及经验。专家评价的过程可能因个人经验不同而存在偏差，在进行实际评估分析工作时为避免意见过度趋同，需要选择不同经历、职业等的评估人员，有利于提高评估的客观性与全面性。

此外，专家评价存在偏差，在进行意见聚合时有必要综合考虑评价人员的基本情况。考虑专业职位、工作时间、教育水平3 个指标确定评价人员权重，计算过程如式（12）和式（13）所示。

xij为专家Ei（i=1，2，…，m）在评价指标j（j=1，2，…，n）下的评分，X为所有评价人员在所有指标下的评分矩阵。

式中：W(Ei)为专家Ei的权重。

2.3.2 基于Tω 的专家意见聚合

多位评估人员针对某一事件的评估结果必然会有一定偏差，因此需要对意见进行聚合以取得共识。不同意见的共识程度与评价专家的重要度都是聚合过程的重要参数，相似聚合法能够综合考虑专家权重与意见共识程度，提高汇总结果的可靠性。此外，在意见聚合计算过程中，存在不确定性的累积问题，Tω 范数能够在保持模糊数形态的同时进行模糊运算，减小可靠性区间的宽度，降低模糊累积影响。

综上，采用相似聚合法对多个TIFN 进行聚合，同时引入Tω 范数提升聚合准确性。基本过程如图4 所示。

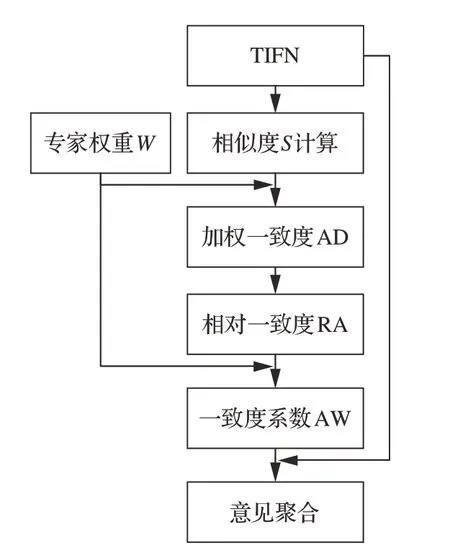
图4 基于Tω 的专家意见聚合过程Fig. 4 Expert opinion aggregation process based on Tω

1）评价相似度计算

专家Es与专家Ek对某一事件的评估结果转化为TIFN 分别为与，则两模糊数的相似度函数S为

2）加权一致度计算

考虑评价人员权重，计算意见一致性。专家Es的加权一致度为

式中：m为专家数量。

3）相对一致度计算

依据加权一致度AD（Es）计算专家Es意见的相对一致度。

4）聚合权重计算

结合专家权重与相对一致度计算专家Es的聚合权重。

式中：β（0≤β≤1）为专家权重与相对一致度的相关因子。

5）基于Tω 算子的意见聚合

基于Tω 算子的专家意见聚合，得到某一事件的综合模糊数。

2.4 解模糊处理

将专家意见聚合得到的综合模糊数转化为失效概率数值包括2 步，即首先将综合模糊数转化为0～1 之间的直觉模糊失效概率（Intuitionistic Fuzzy Failure Probability，IFFP），再将IFFP 转化为失效率数值。

2.4.1 综合模糊数解模糊

采用质心法将综合模糊数转化为直觉模糊失效概率，对于直觉模糊数为隶属度函数，(x)为非隶属度函数：

则直觉失效模糊数IFFP 为

对于三角直觉模糊数=(a，b，c；a'，b'，c')，对应IFFP 为

2.4.2 IFFP 转化为失效概率

文献［13］提出模糊失效可能性与失效率的转化方法，能够实现人的定性感知与适当物理数值的对应并已经在许多领域的研究中得到应用。但不同行业常用的失效概率分级标准差异，使得该方法并不能完全适用。针对民机适航安全领域普遍接受的概率分级方式，保留文献［18］提出的人的感知与物理数值对应的合理趋势，提出相应的改进算法实现IFFP 与失效率（FR）（每飞行小时）的转化算法，如式（23）和式（24）及图5 所示。

2.5 基于直觉模糊贝叶斯网络的定量分析

在构建多阶段任务系统的贝叶斯网络模型并确定数据模糊的叶节点、以融合Tω 算子的IFS理论计算模糊节点失效率之后，依据式（9），结合网络结构及参数进行系统任务可靠性计算。

3 HUD 系统多阶段任务可靠性分析

3.1 HUD 系统

HUD 系统能够将机上各传感器信息处理计算后，经光学成像设备投射至飞行员前方的成像板上，飞行员不需低头查看仪表即能获取必要飞行状态信息，以及告警、故障等提示信息，同时能够实现滑跑起飞指引、拉平指引、进近导引等一系列直观飞行指引信息显示。

HUD 系统的基本架构由平视显示计算机（Head-Up Display Computer，HDC）、平显成像装置（Head-Up Display Imaging Device，HID）、折转显示仪（Foldable Display Device，FDD）组成。其中HDC 接收大气数据计算机、惯性基准系统、无线电高度表、仪表着陆系统、微波着陆系统、测距设备、甚高频全向信标、自动定向仪等诸多传感器信息并进行处理计算，生成显示画面。HID对显示画面进行畸变校正，并经过光学结构进行投影。FDD 接收投射的显示画面并显示飞行员。

HUD 系统在全飞行阶段为飞行员提供飞行状态信息显示与飞行导引。通常，巡航任务在飞机飞行的全任务阶段占比最大，而进近任务则最能够体现HUD 系统的导引功能优势，以巡航、进近两运行阶段为例进行计算。巡航与进近阶段HUD 系统结构如图6 和图7 所示。巡航时长为T1=1.2 h，进近时长为T2=0.4 h。对于巡航阶段，HUD 系统在数据处理环节进行处理结果确认，确认接口数据传输及数据处理结果一致后进行符号画面生成。对于进近阶段，需进行导引能力确认、数据处理结果确认与生成画面确认并得到一致结果，而后输出生成画面。图中蓝色数据流为HUD 系统实现画面显示功能的主数据流，绿色数据流用于数据确认模块实现确认功能。

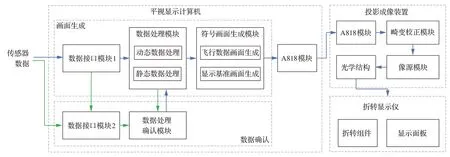
图6 巡航阶段HUD 系统结构Fig. 6 HUD system structure in cruise stage

图7 进近阶段HUD 系统结构Fig. 7 HUD system structure in approach stage

为便于后续分析计算，对上述2 阶段中HUD系统模块、组件及子系统进行编号，如表6 所示。HUD 系统的巡航、进近任务中，元件X13、X14 失效数据模糊，此外还存在CC1、CC22 个共因事件。其他与任务相关的元件/模块的失效率（每飞行小时）如表7 所示。

表6 HUD 系统任务组件编号Table 6 HUD system task components ID

表7 任务相关元件/模块失效率Table 7 Failure rate of mission-related components/modules

3.2 基于直觉模糊贝叶斯网络的HUD 系统可靠性分析模型构建

3.2.1 HUD 系统多阶段任务贝叶斯网络模型

构建HUD 两阶段任务的贝叶斯网络模型，如图8 所示。图中A、B 分别表示巡航阶段与进近阶段，TA、TB 分别为两阶段节点，S 为系统整体任务节点。

图8 HUD 系统巡航-进近阶段贝叶斯网络Fig. 8 Bayesian network in cruise and approach stages of HUD system

3.2.2 考虑共因失效的HUD 系统任务模型

HUD 系统在巡航任务中，元件X13、X15 可能受到共因事件CC1影响，在进近任务中元件X14、X15 可能受到共因事件CC2影响而失效，两共因事件相互独立，且受影响元件皆为确定型共因失效。依据2.1.3 节引入共因空间节点CCE 对网络模型进行扩展，如图9 所示。

图9 考虑共因失效的HUD 系统巡航-进近阶段贝叶斯网络Fig. 9 Bayesian network in cruise and approach stages of HUD system considering common-cause failures

3.3 定量分析

3.3.1 行业专家评审与权重计算

HUD 系统在巡航、进近任务过程中，元件X13、X14 的失效概率模糊，共因事件CC1、CC2发生概率模糊。3 位行业专家对4 个进行评估，评估人员3 项指标量化情况及权重如表8所示。依据表4 中分级编号进行评估，结果如表9所示。

表8 评估人员量化指标Table 8 Evaluators quantification indicators

表9 评价结果Table 9 Fuzzy event evaluation results

3.3.2 意见聚合及解模糊

依据基于Tω 的意见聚合算法及IFFP 与失效 率转换 算法对X13、X14、CC1、CC2等模糊 事件的初步评估结果进行聚合与解模糊处理。以元件X13 为例进行聚合与解模糊计算，如表10和表11 所示，所有模糊事件的计算结果如表12所示。

表10 元件X13 专家评价结果Table 10 Expert evaluation results of component X13

表12 HUD 系统模糊事件的聚合及解模糊计算结果Table 12 IFFR and FR calculation results of HUD system

3.3.3 HUD 系统任务可靠度计算

1）共因失效相关节点参数计算

① 共因空间节点参数。对2 个共因事件组成的共因空间进行划分，形成4 个不相交的共因子空间，并计算其相应概率，形成共因空间节点概率表见表13。

表13 CCE 节点概率表Table 13 Probability table of CCE

② 元件节点参数。对可能收到共因事件影响的元件节点，即X13、X14、X15 进行参数修正。元件X13 在TA 阶段可能受CC1，即共因子空间CCE1、CCE3影 响，元 件X14 在TB 阶 段 可 能 受CC2，即共因子空间CCE2、CCE3影响。元件X15在TA 阶段可能受CC1影响，在TB 阶段可能受CC2影响，即可能受CCE1、CCE2、CCE3影响。以元件X14 为例进行参数计算，TA和TB分别为TA、TB 阶段的持续时间。

依据式（11），在阶段TA 中，对于元件X13，j=1，m=1，则：

对于元件X15，j=1，m=1，则：

在阶段TB中，对于元件X14，j=2，m=1，则：

对于元件X15，j=2，m=1，则：

2）HUD 系统巡航-进近任务可靠度计算与分析

依据表7 和表11 中失效数据及考虑共因失效的节点参数计算结果，计算HUD 系统的巡航-进近阶段任务可靠度（考虑或不考虑共因失效），结果如图10 所示。

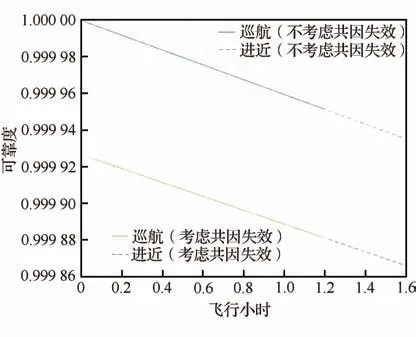
图10 考虑与不考虑共因失效的HUD 系统巡航-进近阶段任务可靠度对比Fig. 10 Comparison of mission reliability of HUD system in cruise and approach stages with and without common-cause failure

表11 元件X13 的聚合及解模糊计算Table 11 Polymerization of element X13 and its de-fuzzification calculation

当不考虑共因失效时，HUD 系统巡航-进近任务进行至1.6 飞行小时，系统任务可靠度为0.999 935 1。考虑共因失效时，任务进行至1.6飞行小时，系统任务可靠度为0.999 865 8。

在模糊评价聚合阶段，如不采用基于Tω 算子的模糊数聚合，上述4 个模糊事件的聚合及解模糊计算结果如表14、表15 所示。

表14 不采用Tω 算子的模糊事件聚合结果Table 14 Fuzzy event aggregation results without Tω

依据表15 中解模糊结果，考虑共因失效影响，计算HUD 系统巡航-进近阶段任务可靠度，当任务进行至1.6 飞行小时，系统任务可靠度为0.955 526 8。采用与不采用Tω 算子进行模糊数聚合的系统任务可靠度对比如图11 所示。其中采用Tω 算子进行模糊数聚合所得的任务可靠度参照左侧坐标轴，不采用Tω 算子所得的可靠度参照右侧坐标轴。可靠度差值趋势如图12 所示，当任务进行至1.6 飞行小时，不采用Tω 算子将使得可靠度降低0.044 34，误差达到约4.4%，由此可见Tω 算子能够一定程度上减轻模糊累积问题带来的计算偏差。

图11 采用与不采用Tω 算子进行模糊数聚合的系统任务可靠度对比Fig. 11 Comparison of task reliability of fuzzy number aggregation system with and without Tω operator

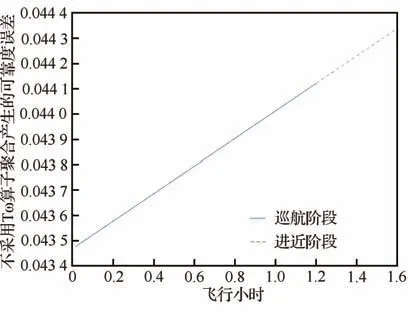
图12 采用与不采用Tω 算子进行模糊数聚合的系统任务可靠度差值Fig. 12 Task reliability difference of fuzzy number aggregation system with and without Tω operator

表15 不采用Tω 算子的模糊事件解模糊结果Table 15 Fuzzy results of solution without Tω

4 结 论

提出基于直觉模糊贝叶斯网络的HUD 多阶段任务可靠性分析方法，能够在底层可靠性数据缺失的情况下进行可靠性分析，并综合考虑了可能出现的共因失效问题。①构建待分析系统任务的贝叶斯网络模型，对于多阶段任务构建PMS-BN 模型，并综合考虑可能的共因失效影响，对PMS-BN 模型进行扩展构建PCCF-PMS模型；②对模型中模糊事件进行定性语言评价并转化为对应模糊数，经过基于Tω 的意见聚合及适当的IFFP 与失效率转化，得到最终聚合结果；③综合模糊聚合结果及其他确定数据，依据PCCF-PMS 模型进行可靠性计算。

基于直觉模糊贝叶斯网络的多阶段任务可靠性分析方法是直觉模糊理论与贝叶斯网络可靠性分析的综合，应用直觉模糊理论对贝叶斯网络中的模糊事件进行评估。提出了适用于航电设备的模糊数定义及IFFP 与失效率转化方法，避免转换算法与航电设备失效概率空间不匹配带来的转换偏差。将基于Tω 的意见聚合应用于贝叶斯网络可靠性分析，降低多重模糊累积带来的聚合误差。

所提方法为缺乏设备服役经验、底层失效数据模糊情况下的可靠性分析提供可行思路，提出适用于航电设备的IFFP 与失效率转换方法。但目前对于该环节转换方法的研究并未深化至模块/组件级别，对电子模块、包含机械结构的模块、光学结构组件等不同模块采用同样的转化方法依然可能带来一定误差。因此，对模块/组件的具体类别及失效特点进一步分析，提出更细化的转换方法以提升模糊分析的准确性将是后续研究的关注重点。