基于小波变换的电力计量数据融合方法

张诗慧，张丰绪

（国网北京海淀供电公司，北京 100085）

0 引 言

随着电网跨越式发展的不断推进，电力设备的规模不断扩大，对于人员配置的需求也逐渐提高[1]。为了缓解由此带来的电力系统管理成本问题，利用现代科学技术实施对电力装置的运维管理是十分必要的[2]。在先进技术手段应用程度逐渐加深的背景下，电力设备对应的状态可以直观地通过具体的计量数据分析计算得到[3]。但是值得注意的是，由设备运行状态形成的电力计量数据链具有多元化、海量化的特点，要实现从不同的层面全面分析电力数据，设计一种更加系统化的数据处理方式必不可少[4]。对于数据处理方法的要求，一方面要能够客观反映设备的实际状态，另一方面要能够对设备的异常情况做出准确判断，这也是保障后续设备运维工作能够具有更强针对性的重要基础[5,6]。考虑到电力系统中的构成设备种类较多、数量也较大，要实现全面掌握设备运行状态，就需要对电力设备的运行数据进行有机整合[7]。在此基础上，本文提出基于小波变换的电力计量数据融合方法，充分考虑了电力计量数据的多样化属性，在利用小波变换对原始电力数据进行预处理后，实现了对数据的有效融合。

1 电力计量数据融合方法设计

1.1 基于小波变换的数据预处理

由于电力计量数据本身具有多样化属性特征，并且数据中也存在一定的噪声，这都在一定程度上影响着最终数据融合的效果。基于此，本文利用小波变换的方式对电力计量数据进行预处理。其中，阈值函数的设置是影响数据预处理效果的关键因素。本文设计阈值函数可以表示为

式中：di,j表示小波变换处理过程中的小波系数参量；ai,j表示原始的小波系数参量；k表示具体的阈值参数；n为正整数；i和j表示小波分解的执行尺度和原始电力计量数据的尺度参数。通过对式（1）进行分析可以看出，本文设计的小波变换阈值函数仍然保留了原有的连续性，这种只有软阈值函数具有的连续性特点能够使得电力计量数据在预处理阶段不会受到数据自身不稳定性的影响。当|ai,j|≥k时，本文设计的阈值函数能够在短区间内实现迅速更新，并且快速逼近硬阈值函数，有效避免了软阈值函数中的固定偏差对于数据处理效果的影响。不仅如此，结合式（1）可以看出，本文设计的阈值函数保留 Garrote 阈值函数的形式，并且引入了参量，通过结合实际电力计量数据的情况对n的取值进行适应性调节，可以保障函数的逼近速度能够满足数据的处理要求，适应大规模电力计量数据的融合需求。当电力计量数据中存在数量较多的尖峰震荡参数时，可以通过增大n值的取值结果，提高小波变换的平滑能力。当电力计量数据中存在数据丢失问题时，可以通过减小n值的取值结果，提高小波变换的信息保留能力。

利用上述设置的阈值函数对原始的电力计量数据进行小波变换处理的方式可以表示为

式中：f(m)表示小波变换处理后的电力计量数据信息；m表示小波变化的尺度因子；x(t)表示原始的电力计量数据参数。

通过式（2）可以看出，本文采用连续小波变换的方式对电力计量数据信息进行处理，在阈值函数范围内将数据分解为多个参量，使得数据的动态发展情况转变为多个相对独立的数据点。

通过这样的方式，完成对电力计量数据的预处理，为后续的数据融合提供基础。

1.2 电力计量数据融合

利用小波变换后的数据，本文对于电力计量数据的融合是根据数据的属性进行的。通过处理，原始的电力计量数据已经转化为分解的独立个体，本文首先对数据进行分类处理，具体的分类方式可以表示为

式中：B(x)表示对分类结果；E表示计量数据对应设备的额定运行参数。按照式（3）所示的方式，电力数据的分类结果共分为2类，其中一类是数值小于E的分类，该类数据表示电力计量数据处于低负荷运行模态，对应的输出低于额定值。另一类为数值大于E的分类，该类数据表示电力计量数据处于高负荷运行模态，对应的输出高于额定值。以此为基础，分别对2类数据进行融合计算，得到的电力系统整体运行状态数据信息可以表示为

式中：F(x)表示融合后的电力计量数据信息；也就是整个电力系统的运行状态参数；B1(x)表示电力计量数据低于额定数值的参数；Bh(x)表示电力计量数据高于额定数值的参数。对应地，∑B1(x)和∑Bh(x)分别表示2类数据的参数之和，也就是不同类型数据的实际规模。

通过这样的方式，实现对电力计量数据的融合处理，为电力系统整体运行状态的分析和判断提供便利。

2 测试与分析

2.1 测试环境

在对本文设计的数据融合方法进行测试的过程中，为了提高测试结果的分析价值和可靠性，为测试设置了对照组。其中，对照组分别采用了文献[2]提出的基于三维时空特性的数据融合方法、文献[3]提出的基于大数据的数据融合方法。在测试数据准备上，本文以某电力企业的电力设备运行数据为基础，采集了所有计量装置的参数信息，具体的采样频率为1个/h。按照这样的方式，单日获取电力数据的样本中包含 24 个样本点。图1为单日采集数据的分布情况。

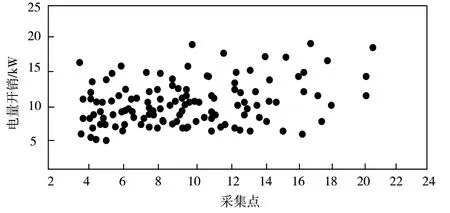
图1 单日采集结果分布图

在此基础上，连续采集7天。分别采用上述4种方法对电力运行数据进行融合处理，分别统计单日电力系统的实际电量供求关系。对于最终融合结果的分析，本文通过单独计算各个电力设备运行数据之间的关系，得到实际的电力系统运行情况。将对应的结果作为评价基准，对3种方法的融合结果进行分析。

2.2 测试结果与分析

以2.1节的数据为基础，分别统计了3种不同融合方法下，得到的电力系统运行情况与实际数据之间的关系，具体如表1所示。

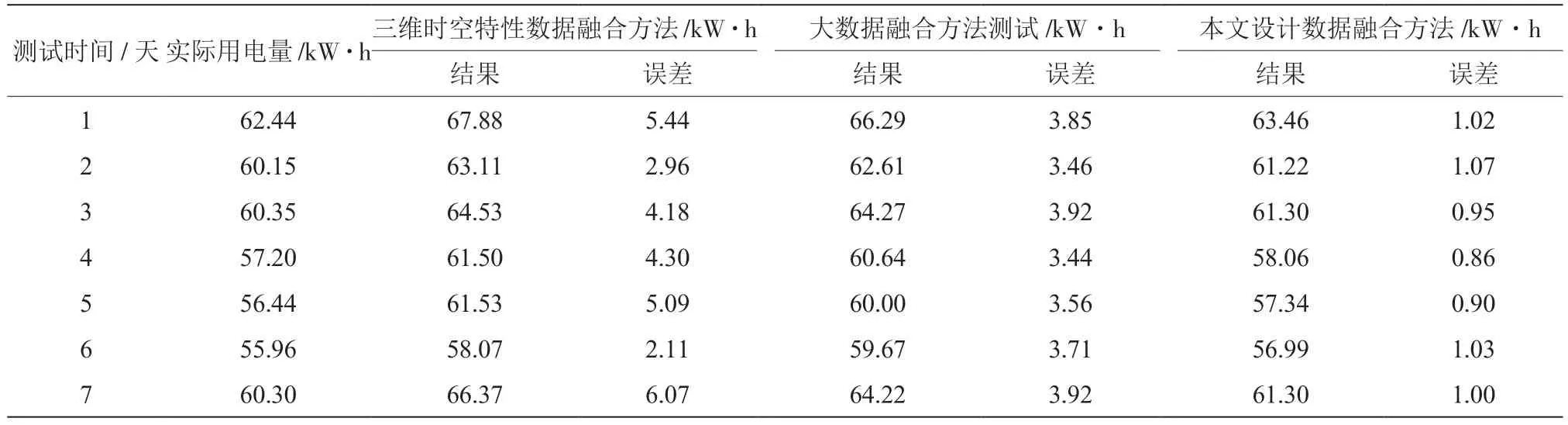
表1 电力系统综合运行数据统计表

通过对表1中的数据信息进行分析可以看出，在3种测试方法中，三维时空特性数据融合方法对于数据的融合结果与实际电力系统运行数据之间的差异最为明显。这种差异表现出了明显的不稳定性，单日最大误差达到了6.07 kW·h，对应的占比为10.07%；最小误差为2.11 kW·h，对应的占比为3.63%。大数据融合方法的测试结果中，实际电力系统运行数据之间的差异虽然具有较高的稳定性，但是整体水平偏高，基本稳定在3.00～4.00 kW·h，对应的占比6.63%。相比之下，本文设计数据融合方法下，得到的电力系统综合运行数据与实际电力系统运行数据之间的差异最小，且稳定性较高，最大值仅为1.07 kW·h，对应的占比为1.78%。通过上述对测试结果的分析不难看出，本文设计的基于小波变换的电力计量数据融合方法可以实现对多源数据信息有效整合，在准确反映电力系统实际运行状态方面具有良好的应用价值。

3 结 论

为了适应电力系统的发展需求，对相关电力数据进行高效管理是极为必要的。本文提出基于小波变换的电力计量数据融合方法研究，借助小波变换对于电力计量数据中噪声的过滤能力，提高了数据融合的质量，使得最终的融合数据能够更加准确地反馈电力设备的实际运行状态。通过本文的研究，希望能够为实际的电力系统管理工作开展提供有价值的参考，助力电力系统实现长期、安全、稳定运行。