初中数学大概念教学中的高阶思维能力培养

李佳嘉

传统的数学教学往往侧重于直接教授概念和解题方法，学生则通过重复练习来掌握知识。然而，这种方法并不足以培养学生的高阶思维能力。为此，现代教育越来越强调以学生为中心的教学方法，更加关注如何提升学生的思考、探究和创新能力。

例如，在教授“一元一次方程”时，教师可以创设实际问题的情境，激发学生探究方程背后的数学原理，而不仅仅是学习如何解方程。通过这种方法，学生可以更深入地理解方程的应用，而不是只停留在表面的符号操作。此外，教师可以鼓励学生提出问题和参与讨论，帮助他们从不同角度思考问题，从而拓宽学生的思维和视野。

在教学中，培养创新思维是一个关键环节。教师可以指导学生尝试多种解题方法，并鼓励他们创造自己独特的解题方法，从而帮助学生发展独立和创新的思维模式。

一、以问题为导向，培养学生的思考能力

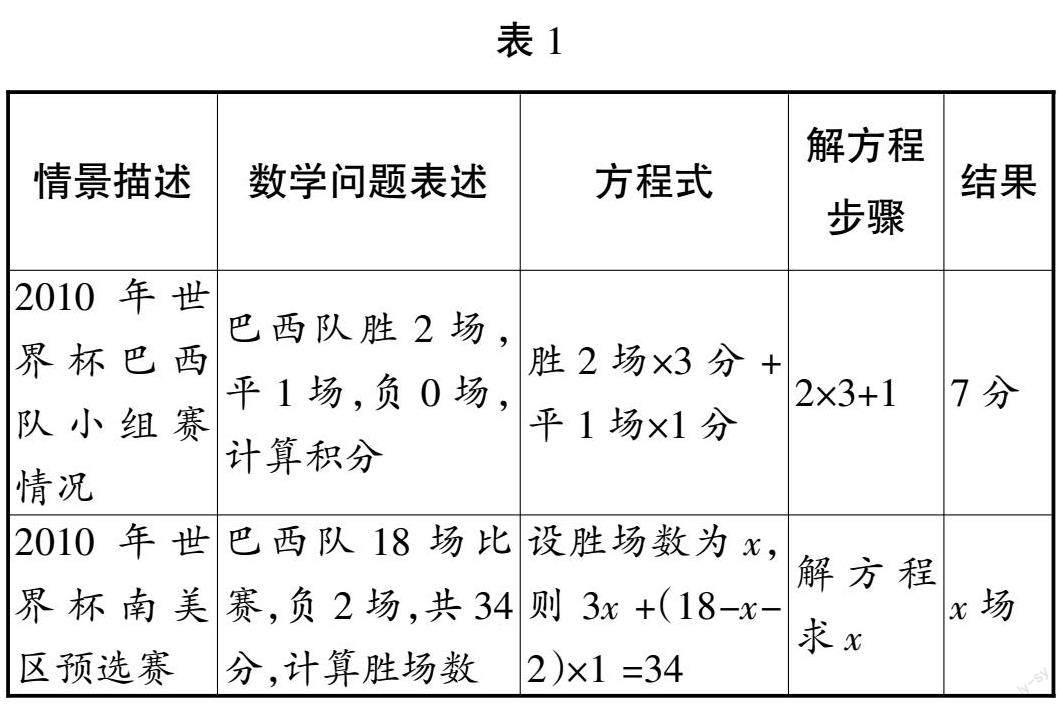
师：（播放2010年南非世界杯宣传曲）同学们，让我们回顾一下2010年南非世界杯。巴西队在小组赛中的表现如何？他们胜了几场？

生1：老师，我记得巴西队胜了2场。

师：很好，那么他们的积分是多少呢？

生2：每胜1场得3分，巴西队是6分。

师：正确。现在让我们看一道更有挑战性的题。在2010年世界杯南美区预选赛中，巴西队共参加了18场比赛，只负了2场，总共得34分。那么，他们胜了多少场比赛呢？

（学生开始尝试解答，但有些困难）

生3：老师，这道题好像不能用简单的算术来解决。

师：观察得很仔细，这就是我们今天要学的内容“一元一次方程”，让我们用方程来解决这个问题。

（教师引导学生通过设方程来解决问题）

师：看，通过使用方程，我们不仅解决了这个问题，还体会到了数学从算术到方程的进步。你们认为在解决实际问题时，使用方程有哪些优势？

学生积极讨论，分享想法。

（设计意图：這一教学活动的目的在于通过实际且富有趣味性的问题来引导学生思考，并展示数学概念如何在现实世界中的应用。选择2010年南非世界杯的相关问题不仅能激发学生的学习兴趣，还能帮助他们理解数学概念在实际情境中的应用。通过这种方法，学生能体会到数学从算术到方程的进步，并理解方程在解决实际问题中的重要性和实用性。）

此外，教师运用这种教学方法，学生的课堂参与度较高，能培养他们的团队合作精神和沟通技巧。通过师生互动和小组讨论，学生不仅学习了数学知识，还锻炼了批判性思维和问题解决能力。这样的教学设计旨在使教学更加生动和实用，同时培养学生的高阶思维能力。以问题为导向的教学方法在初中数学教学中培养高阶思维能力方面具有重要意义。通过实际问题的引导，学生不仅学会了数学概念的应用，还锻炼了团队合作、沟通、批判性思维和创新思维等多方面的技能。这些技能将在他们未来的学术生涯和职业生涯中发挥重要作用，使他们更有能力面对复杂的挑战和问题。因此，教师应积极探索和采用这种教学方法，为学生的综合发展提供更好的支持和指导。

二、创设教学情境，提升学生的探究能力

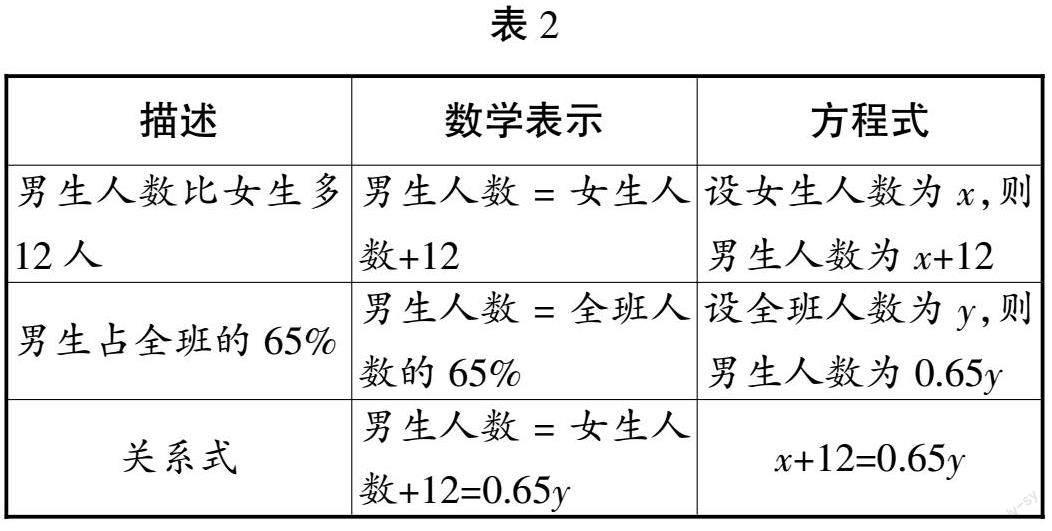
师：七年级（2）班的男生比女生多12人，男生占全班人数的65%。我们该如何得出班级的总人数呢？

生1：这个问题好像和我们之前学的比例有关。

师：非常好的观察，那么我们怎样才能用方程来表示这个问题呢？

生2：我们可以设班级总人数为x，然后建立方程来表示这个关系。

师：很好，那么方程应该是怎样的呢？

（学生2和其他学生在黑板上尝试建立方程。）

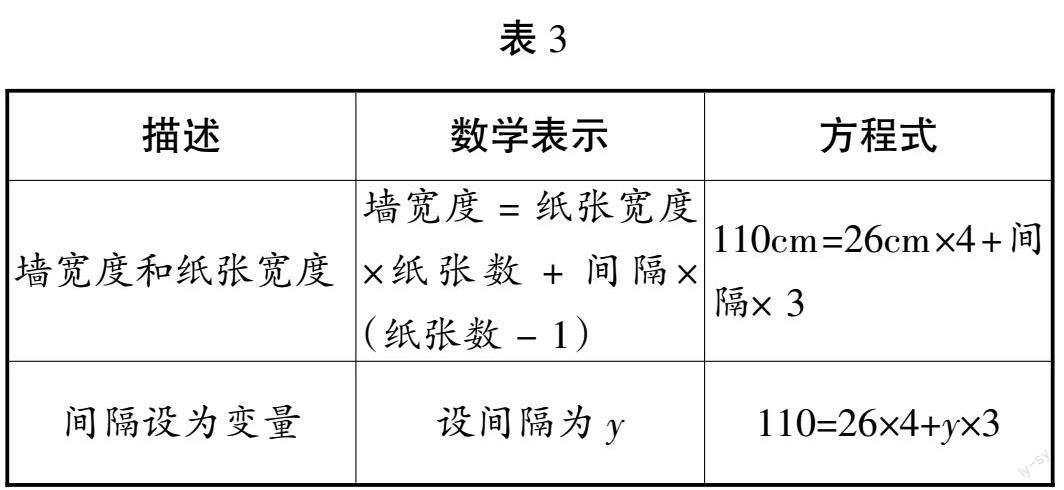
师：现在，让我们用同样的方法来解题。测量一面墙的宽度为110cm，每张纸的宽度为26cm，横向可以放4张纸。我们需要找出相邻两张纸的间隔。这个问题应该怎样用方程来表示呢？

生3：我觉得可以设间隔为y，然后用这个变量建立方程。

师：非常好。请你来尝试一下。

（学生3和其他学生在黑板上探讨并建立方程）

（设计意图：创设教学情境的目的是让学生在解决与实际生活紧密相关的问题时，体会到数学的应用价值。通过这种方法，学生不仅能够理解和运用数学概念，还能提升他们的探究能力和实际应用能力。选择生活中的具体问题作为教学内容，可以更好地吸引学生的注意力，使他们更加投入、积极地参与到学习中。）

此外，这种教学方式鼓励学生合作和交流，有助于培养他们的沟通能力和团队合作精神。通过集体讨论和解决问题，学生能够更好地理解数学概念，并将这些概念应用于具体情境中。这样的教学方法不仅能够提升学生的学习兴趣，还能有效提高他们的思考能力和解决问题的能力。学生不再满足于表面的答案，而是追求深入的理解和更好的解题方法。他们学会了提出问题、思考解决问题的方法、建立方程、分析数据，这些能力在解决日常生活中的各种问题时都非常有用。

三、鼓励学生提问，发散学生的思维

师：我们已经学习了“一元一次方程”的基础概念。有谁对今天讲的内容有疑问吗？

生1：老师，为什么我们要用方程来解这些问题？直接计算不是更简单吗？

师：很好的问题。方程能帮助我们更系统和抽象地理解问题。其他同学呢，还有什么问题吗？

生2：老师，“一元一次方程”除了解这类问题外，还能用在哪些地方呢？

师：这是一个非常实际的问题。方程在许多领域都有应用，如物理、工程等。

生3：老师，我想知道，如果问题变得更复杂，我们还能用“一元一次方程”来解决吗？

师：这取决于问题的具体情况。对于更复杂的问题，我们可能需要用到更高级的数学工具。但“一元一次方程”是一个很好的起点。

学生继续提问，教师鼓励他们思考并解答问题。

师：看来大家都很好奇并且有很多问题。那接下来就通过问题来拓展我们的知识。

（设计意图：鼓励学生提问的主要目的是激发他们的好奇心和思考能力。在教学中，学生提出的问题不仅可以帮助他们理解和巩固新知识，还能促进他们的批判性思维和创造性思维的发展。通过提问，学生能够从不同的角度探索和理解数学概念，从而加深对这些概念的理解。）

此外，这种互动式的教学方式还能提高学生的参与度和学习兴趣。学生在提问和回答问题的过程中，不仅可以表达自己的想法和观点，还能听取其他同学的观点，从而促进知识的共享和交流。这样的教学方法能为学生提供开放和包容的学习环境，鼓励他们自由地表达和探索，最终发展思维的广度和深度。鼓励学生提问是教育中的重要组成部分，可以激发学生的好奇心、培养他们的思考能力、提高参与度和兴趣。因此，教师应积极鼓励学生提问，并给予他们足够的空间和时间来思考和探索，以培养他们全面发展所需的思维广度和深度。

四、创新思维训练，加深学生的思维深度

师：今天，我们将进行一项特别的活动，旨在训练大家的创新思维。我提一个问题，你们提出至少两种不同的解决方案。准备好了吗？

生1：我们准备好了，老师！

师：假设你们需要计算某个商品在打折后的价格，原价是100元，打8折。尝试用不同的方法来解这个问题。

生2：第一种方法，我们可以直接计算100乘以0.8得到80元。

师：很直接的解法。有没有第二种方法呢？

生3：我们可以先计算出不打折的部分，即100乘以0.2，然后用原价减去这部分。

师：很好。现在，谁能再提出一个不同的问题，让我们一起尝试用不同的方法解答？

生4：如果一个人的年龄是另一个人的2倍，总年龄是60岁，他们各是多少岁？

学生开始讨论，提出不同的解法。

师：同一个问题有多种解决方法，每种方法都有其独特之处。这种思考方式可以帮助我们更深入地理解问题，并培养我们的创新思维。这就是今天要学习的——不满足于单一的解题方法，而要不断探索和创新。

（设计意图：创新思维训练的目的是培养学生的创造力和解决问题的多样性。通过鼓励学生对同一问题提出多种解决方案，不仅能加深他们对问题的理解，还能培养他们从不同角度思考和解决问题的能力。这种训练有助于学生摆脱思维定式，提高他们的想象力和创新思维。）

此外，这种教学方法鼓励学生自主学习和探究。在寻找解题方案的过程中，学生需要运用已有的知识和技能，积极思考新的解题方法。这样的学习能够提高学生的参与度，促进他们批判性思维和创造性思维的发展。通过这样的训练，学生可以逐渐养成独立思考和解决问题的习惯，为他们未来的学习和生活打下坚实的基础。这种训练有助于培养学生的自信心，使他們学会在面对复杂问题时不怕失败，而是积极尝试各种可能的解决方案。这样的心态将对他们未来的学习和职业生涯产生积极影响，能使他们更有能力面对各种挑战和问题。

通过以上四个教学环节，我们可以看到，这种多维度、互动式的教学方法对初中数学教学，特别是“一元一次方程”的教学是非常有效的。

首先，问题导向的学习方法激发了学生的好奇心和探索欲，促使他们积极参与到学习中。通过将数学概念应用于实际问题，学生能够更好地理解和记忆这些概念。其次，教师创设与学生生活紧密相关的教学情境，能使抽象的数学知识变得更加生动和具体，提升学生的探究能力。此外，教师鼓励学生提问和思考不同的解决方法，不仅发散了他们的思维，还培养了他们的批判性思维和创造性思维。最后，通过创新思维的训练，学生学会了从多个角度思考和解决问题，这对他们的长期学习极为重要。

这样的教学设计不仅激发了学生对数学学习的兴趣，还发展了他们的创新思维。通过这些教学活动，教师不仅教授学生数学知识，更是在引导他们学会学习、思考和探索，这对他们的终身学习和个人成长至关重要。

（作者单位：昆明市第十中学）

编辑：赵文静