基于KPCA-GWO-SVM 的矿井突水水源识别

2023-03-27华星月邵良杉

煤矿安全 2023年2期

华星月，邵良杉

（1.辽宁工程技术大学系统工程研究所，辽宁葫芦岛 125105；2.辽宁理工学院，辽宁锦州 121000）

矿井突水是威胁煤矿安全生产的重大灾害之一。据统计，“十二五”期间，重大以上水害事故占全国煤矿同类事故起数和死亡人数的23.6%和19.2%，给国家财产和人民生命造成重大损失[1]。因此，快速识别水源类型并采取积极有效措施具有重要的现实意义。

目前，学者提出了众多判别水源方法，包括激光诱导荧光技术[2]、水温水位法[3]、水化学分析法[4]和数理统计分析法[5]等。随着研究的不断深入和机器学习的发展，众多学者以此为基础建立水源识别模型，提高水源识别的精准度。陈绍杰等[6]将水化学分析法与主成分分析-残差分析（PCA-RA）相结合确定梁家煤矿矿井水的补给来源；王甜甜等[7]基于动态权-集对分析建立识别模型，削弱人为因素并确定合理主客观权重比例；周孟然等[8]为识别不均匀分组的突水水源荧光光谱，将飞蛾扑火（MFO）算法与谱聚类（SC）相结合建立模型；纪卓辰等[9]经PCA降维，代入Logistic 回归建立纳林河矿区水源判别模型，进一步提高模型速度；邵良杉等[10]将改进鲸鱼优化算法（IWOA）与混合核极限学习机（HKELM）结合建立识别模型；侯恩科等[11]利用核主成分（KPCA）提取特征，建立KPCA-APSO-ELM 的矿井突水水源判别模型，进一步提高模型的精准度。上述研究一定程度上推动矿井突水水源识别技术的发展，提升水源识别的准确率，但是仍存在局限性；如谱聚类对数据样本要求较高，结果不稳定；极限学习机未考虑结构化风险，易陷入局部最值。

基于此，对突水水源样本数据进行核主成分分析（Kernel Principal Component Analysis, KPCA），消减因素之间的相关性。利用灰狼优化算法（Grey Wolf Optimizer，GWO）对支持向量机（Support Vector Machine, SVM）的惩罚参数与核参数进行寻优，建立KPCA-GWO-SVM 的矿井突水水源识别模型，以快速识别矿井突水水源的类型。

1 理论分析

1.1 核主成分分析

核主成分分析（KPCA）是对主成分分析（PCA）的一种非线性拓展，其基本思想是：通过核函数将在低维空间中线性不可分的数据，通过映射函数将其投射到更高维的空间中去，使之在高维空间中线性可分。KPCA 的具体步骤参见文献［12］。针对因素之间的相关性和数据冗余问题，核主成分分析能有效进行降维。

1.2 灰狼优化算法

灰狼优化算法（GWO）是由SeyedaliMirjalili 等[13]模拟自然界中灰狼群体的社会等级机制和捕猎行为而衍生出的1 种新型群体智能优化算法，主要包括包围、狩猎和攻击3 个阶段。灰狼遵循严格的等级体系，第1 层是狼群中的头狼记为α，负责对捕食、栖息、作息时间等活动做出决策；第2 层记为β 狼，服从并协助α 做出决策；第3 层记为δ 狼，服从α和β，同时支配剩余层级的狼；第4 层记为ω 狼，是等级体系的基础。灰狼种群等级体系如图1。

图1 灰狼种群等级体系Fig.1 Graywolf population hierarchy

在算法进化中，α、β 和δ 分别为历史最优解、次优解、第3 最优解，负责定位猎物的位置，并引导其他个体ω 完成靠近、包围和攻击等行为，最终达到捕食猎物的目的。灰狼搜索猎物时会逐渐地接近猎物并包围它，该行为的数学模型如下：

式中：X 为灰狼位置向量；Xα、Xβ、Xδ分别为当前种群中α、β、δ 的位置向量；X1、X2、X3分别为灰狼向α、β、δ 移动的位置向量；Dα、Dβ、Dδ分别为当前候选灰狼与最优3 狼之间的距离；X（t+1）为移动终点；C1、C2、C3为随机向量；A1、A2、A3为系数向量。

1.3 支持向量机

支持向量机（SVM）是基于统计学习原理的监督学习分类方法，能提供较好的泛化性能和解决高维数、小样本的问题。其基本思想是：通过某种事先选择的非线性映射将输入向量映射到一个高位特征空间中，在这个空间中构造最优分类超平面，从而使得样本之间的分离界限达到最大。SVM 的具体原理参见文献［14］。

1.4 KPCA-GWO-SVM 模型建立流程

针对因素之间的相关性和数据冗余问题，核主成分分析能有效进行降维。灰狼优化算法（GWO）具有较强的收敛性能且参数少，而支持向量机（SVM）的惩罚参数Cp与核参数g 很大程度上影响训练集的学习能力及泛化能力。首先，在迭代过程中保留当前的3 个最优解α、β、δ，对种群进行社会等级分层，为算法的全局寻优能力夯实基础；其次，计算灰狼与猎物的距离，接近并包围猎物，不断更新最优解，集中搜寻使得算法尽快找到全局最优解。以平均均方误差MSE 作为优化的目标函数值，验证算法的鲁棒性。鉴于此，采用灰狼优化算法寻求最优解确定支持向量机的参数，建立基于KPCA-GWOSVM 的水源判别模型，KPCA-GWO-SVM 的水源判别模型流程图如图2。

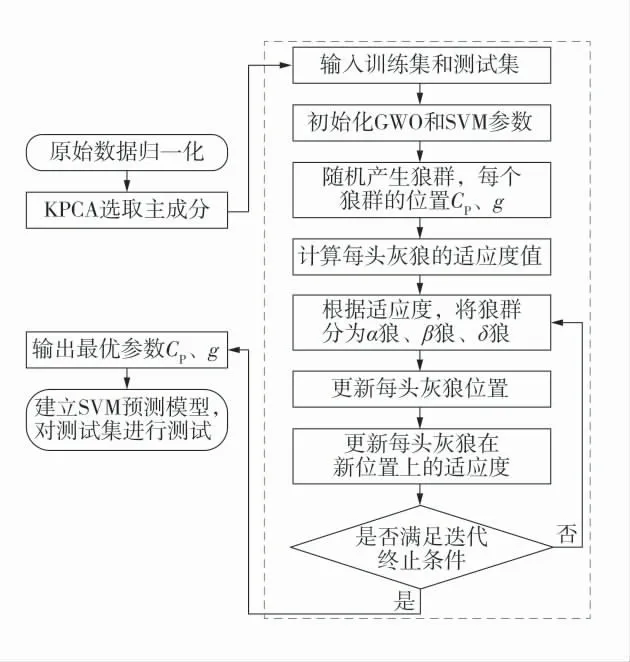
图2 KPCA-GWO-SVM 的水源判别模型流程图Fig.2 Flow chart of KPCA-GWO-SVM water source discrimination model

2 实例应用

2.1 矿区概况

唐山开滦赵各庄矿煤系地层为石炭—二叠系，共7 层可采煤层及局部可采煤层。

矿区的含水层由上到下为：第四纪冲积层空隙承压含水层、A 层以上顶板砂岩裂隙承压含水层、5#煤层-顶板砂岩裂隙承压含水层、5#～12#煤层砂岩裂隙承压含水层、12#～14#煤层砂岩裂隙承压含水层、14#煤层～唐山灰岩砂岩裂隙承压含水层和奥陶系岩溶承压含水层。其中，第四纪冲积层空隙承压含水层以细沙、中砂为主，厚度差异大，水化学类型为HCO3-Ca；煤系地层砂岩裂隙承压含水层的水化学类型主要为HCO3-Na，pH 值在7.04～9.00 之间；奥陶系岩溶承压含水层主要位于古岩溶发育层及构造岩溶裂隙，水化学类型为HCO3-Ca[15]。

2.2 指标选取

以赵各庄矿为研究对象，选取6 种离子作为水源识别的判别指标，分别为：Na+（X1）、Ca2+（X2）、Mg2+（X3）、Cl-（X4）、SO42-（X5）和HCO3-（X6）。根据文献［15］对赵各庄矿1959—2016 年突水类型的分析，选取老空水、奥灰水、13#煤层砂岩裂缝水、12#煤层砂岩裂缝水4 种水样类型，共计67 个样本进行训练与测试。其中老空水记为I，奥灰水记为II，13#煤层砂岩裂缝水记为III，12#煤层砂岩裂缝水记为IV。赵各庄矿样本数据见表1。

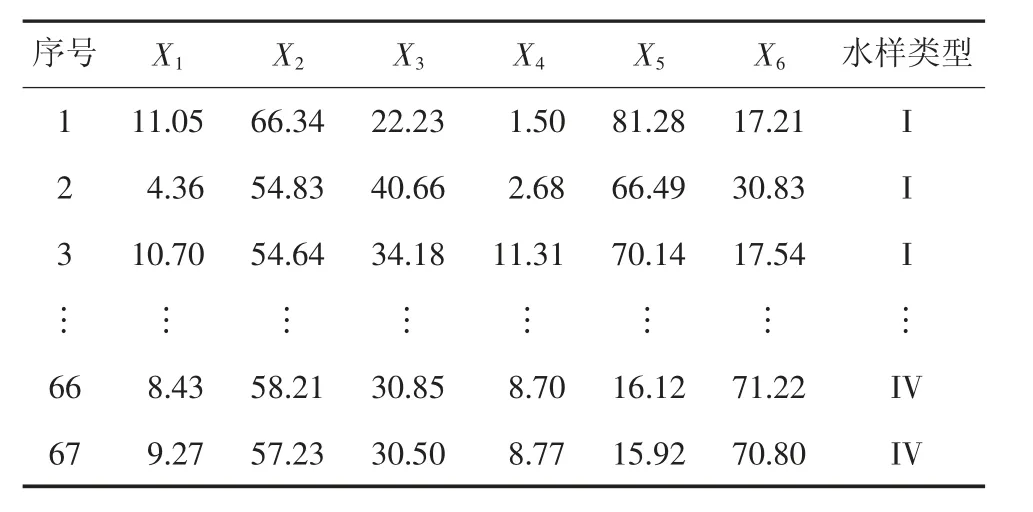
表1 赵各庄矿样本数据Table 1 Zhaogezhuang Mine samples data

2.3 数据相关性分析及KPCA 降维

针对矿井突水原始数据差异较大的问题，进行归一化处理，将原始数据调整到［0，1］之间。随后借用SPSS20 进行相关性分析，指标相关系数表见表2。

由表2 可知：6 种离子之间存在显著程度的相关，其中X5与X6、X4与X5、X4与X6、X2与X3的相关系数分别为-0.987、-0.860、0.800、-0.731，说明存在数据冗余，需要对判别指标进行降维。

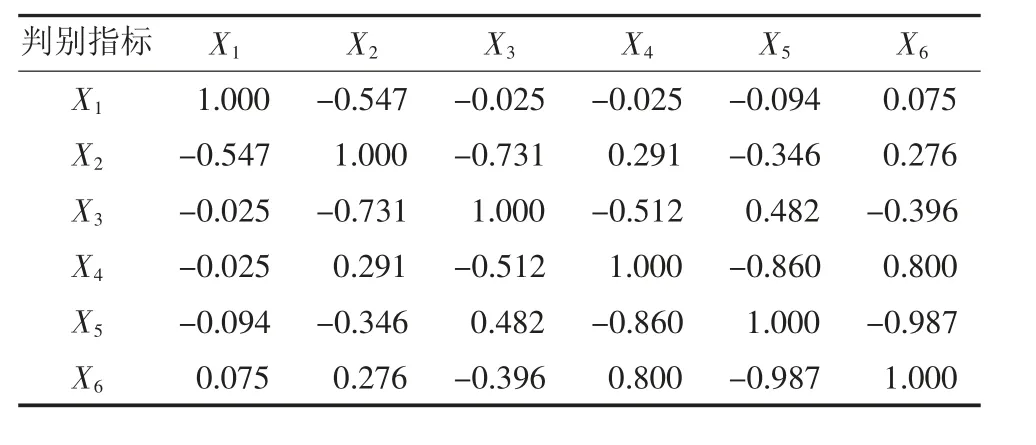
表2 指标相关系数表Table 2 Index correlation coefficient table

利用MATLAB2016 对原始数据进行KPCA 降维，选取标准为累计方差解释大于85%，最终提取3个主成分，分别记为Y1、Y2、Y3（Y4～Y6忽略），对应的解释方差分别为56.96%、24.16%和15.49%，累计解释方差为96.61%，表明提取的3 个主成分可以反映原始6 个离子指标的绝大部分信息。用Excel 绘制特征解释度累计占比图，KPCA 降维后的数据见表3，解释度累计占比图如图3。

表3 KPCA 降维后的数据Table 3 KPCA dimensionality reduction data

图3 解释度累计占比图Fig.3 Chart of cumulative percentage of interpretation degree

2.4 KPCA-GWO-SVM 模型的建立

在矿井突水水源识别模型中，将经由核主成分分析得到的3 个主成分Y1、Y2、Y3作为输入向量，水样类型为模型输出，随机选取总样本量70%为训练集（共47 组），30%作为预测集（共20 组）。利用MATLAB 编写相应程序代码，代入数据，由此建立基于KPCA-GWO-SVM 的矿井突水水源识别模型并对测试集进行预测。同时，将未经KPCA 处理的归一化数据代入GWO-SVM 模型并对测试集进行预测，与经过KPCA 数据预处理数据的KPCA-GWOLSSVM 模型预测结果进行对比。

为进一步验证基于KPCA-GWO-SVM 的矿井突水水源识别模型的精确度和可靠性，在同一个主程序中将KPCA 降维后的数据分别带入建立KPCA-PSO-SVM 模型、KPCA-WOA-SVM 模型和KPCA-SVM 模型，保证对同一测试集进行预测，所得结果与KPCA-GWO-SVM 模型结果进行对比。以平均均方误差MSE 作为优化的目标函数值。模型相关参数表见表4。

表4 模型相关参数表Table 4 Model related parameters table

2.5 结果分析

支持向量机的参数寻优如图4。

由图4（a）和图4（b）可知：在进化代数不到5 次时，KPCA-GWO-SVM 已搜寻到最佳适应度值，此时的最优惩罚参数Cp=1.088 5，核参数g=46.297 2；而未经KPCA 降维处理的GWO-SVM 寻优速度较慢，进化代数20 次左右时才获得最优解，且最佳适应度值较低，分类准确率不高。此时对于随机选取的20个测试样本，KPCA-GWO-SVM 的误判个数为0，分类准确率达到100%，而GWO-SVM 有2 个误判，准确率为90%。由此可见，与GWO-SVM 模型相比，KPCA-GWO-SVM 模型的分类准确率提高了10%。因此，与未经预处理的数据相比，用KPCA 对冗余数据降维，再代入GWO-SVM 模型，能加快模型的寻优速度，是有效而必要的。

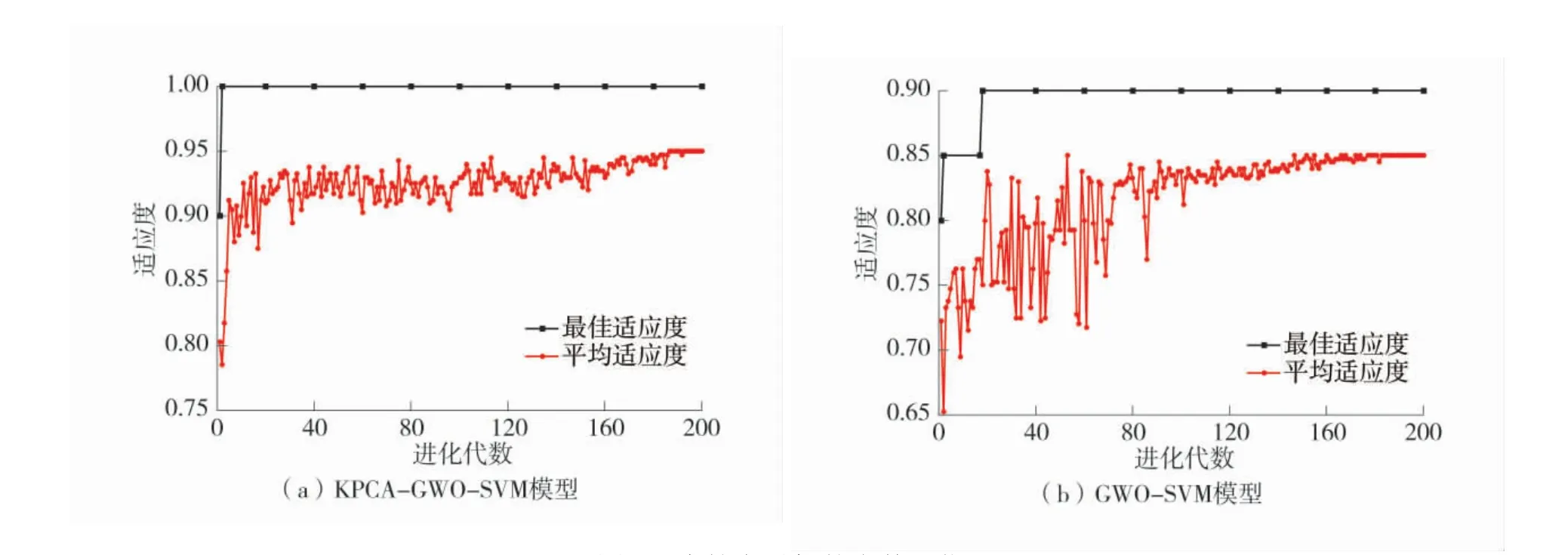
图4 支持向量机的参数寻优Fig.4 Parameters optimization of support vector machine

为进一步验证KPCA-GWO-SVM 模型的优越性，将其结果与KPCA-PSO-SVM 模型、KPCAWOA-SVM 模型和KPCA-SVM 模型进行对比，不同水源判别模型预测结果对比见表5。

表5 不同水源判别模型预测结果对比Table 5 Comparison of prediction results of different water source discriminant models

结果表明：模型的误判率为0，测试集准确率为100%；KPCA-PSO-SVM 模型的误判率为1/5，测试集准确率为80%；KPCA-WOA-SVM 模型的误判率为1/20，测试集准确率为95%；KPCA-SVM 模型的误判率为1/10，测试集准确率为90%；此时KPCAGWO-SVM 模型的平均均方误差为0，KPCA-PSOSVM 模型的平均均方误差为0.2，KPCA-WOA-SVM模型的平均均方误差为0.05，KPCA-SVM 模型的平均均方误差为0.1，因此，模型的均方误差最小，表明所提出的算法具有较好的鲁棒性。由此可见，KPCA-GWO-SVM 突水水源识别模型预测准确率优于其他模型，能准确有效地应用于突水水源类型识别问题。