基于斜抛物线法的空钩下降能力分析研究

聂 宁

上海电气风电集团股份有限公司 上海 200235

0 引言

浮式起重机广泛应用于港口工程、桥梁工程、打捞工程、大型海上军事装备工程、海上风电安装工程、海上油气田开发工程及退役海洋钻井平台拆解工程等，适用于重大件的吊装作业、设备安装作业、水上施工及打捞作业等[1-4]。

在交机验收或现场作业过程中，吊钩组在空载工况下无法顺利下降的情况时有发生。现有文献多以单臂架门座式起重机为研究对象，着眼于吊钩组水平移动轨迹的补偿以及已知挠度条件下吊钩组自重的选取。就钢丝绳最大挠度或悬索长度与吊钩组自重、钢丝绳自重、弦线倾角之间相互关系进行分析，并对吊钩组自重设计不当或钢丝绳挠度过大等情况下可能引发的各类弊端做了论述。但对空钩的实际下放过程，空钩自重设计的合理输入条件，作业循环过程中的下降能力或下放作业效率，下降能力与各主要因素变量的关系，以及所能达到的效果鲜有涉及和探究[5，6]。

本文以浮式起重机为研究对象，从斜抛物线的基本理论入手[7-12]，对起升钢丝绳悬垂段数学模型的线形、张拉力、挠度及弧长方程等进行了详细的理论推导。结合吊钩组的升降运动过程，构建了空钩下降的基本条件，考虑了不同运动状态及其过渡阶段下因速度变化而引起的钢丝绳张拉力差异对悬垂段钢丝绳弧长计算造成的影响。从空钩的下放作业效率出发，将满足下放条件前后悬垂段钢丝绳的弧长变化量即卷筒放绳量以及放绳时间作为表征空钩下降能力的重要参数，论述了变幅下降过程中钢丝绳几何形状的变化特点，总结了钢丝绳张拉力与挠跨比的关系，分析了空钩自重、钢丝绳线密度、速度及加（减）速度等对空钩下降能力的影响。依据求解所得的数据得到有益的结论，获取了较为普遍的规律和趋势，廓清了过往对空钩不下降现象的模糊认识。

1 数学模型

起升钢丝绳作为一个重要的承载部件，广泛与滑轮或卷筒配合使用。通常忽略钢丝绳弯曲刚度，假定其为柔性结构，不承受弯矩和压力，仅能承受拉力。钢丝绳在自重及绳端载荷的联合作用下，一般认为是几何不变的稳定体系，处于平衡状态，其单位长度的质量q沿弦长AB近似均匀分布，如图1所示。

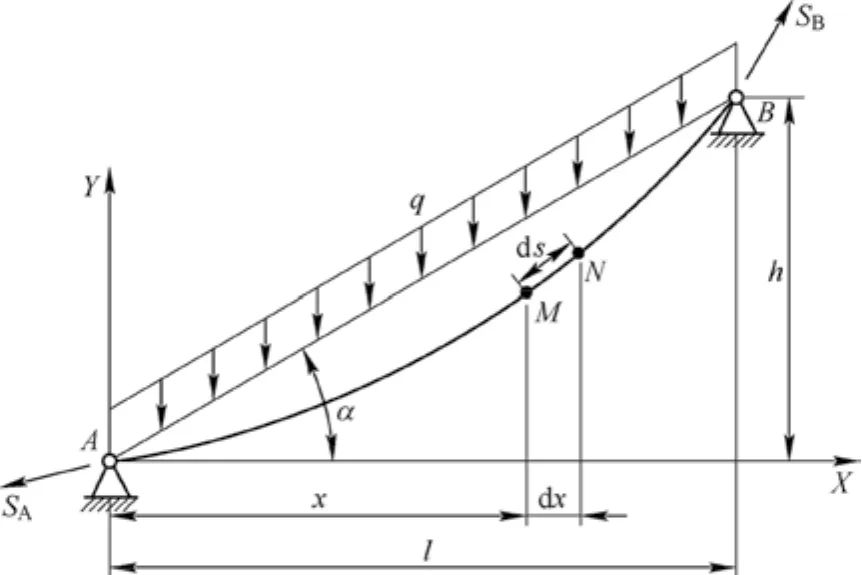
图1 钢丝绳悬垂段的数学模型

由于钢丝绳在滑轮间的水平跨度l较长，吊钩组空载时，在钢丝绳自重的影响下，更容易会产生下挠、悬垂。当滑轮悬挂端A、B高度差值h与水平跨度l之比即弦向斜率k＜15%时，使用平抛物线已足够。而当k≥15%时，应采用更精确的斜抛物线法模拟悬垂钢丝绳的平衡状态，以满足工程精度的需求[7]。

2 理论计算

静态平衡条件下，起升卷筒制动保持，吊钩组空载并位于起升上极限位置，起升钢丝绳保持静止悬垂状态，钢丝绳的内力和结构形状保持不变。

2.1 钢丝绳的线形方程

于钢丝绳悬垂曲线上任取一弧长元素ds，对其平衡形态进行分析求解。弧长段两端张拉力为Si，垂直分量为SVi，水平分量为SHi。将钢丝绳的均布载荷q纳入弧长元素段ds的受力分析中，如图2所示。

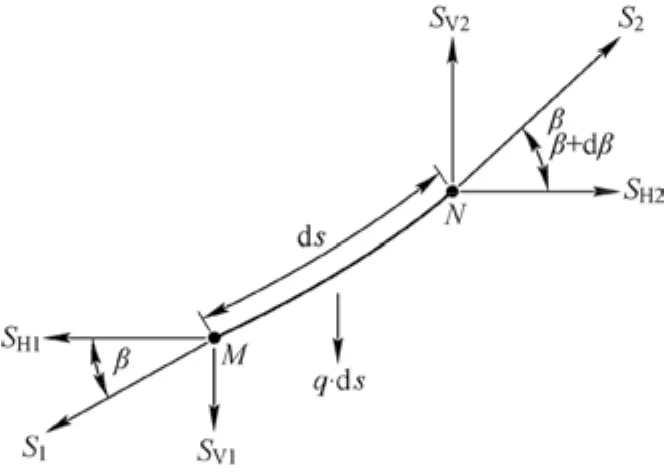
图2 弧长元素ds的受力分析

由平面力系的平衡条件∑X=0可知，钢丝绳的水平张拉力

悬垂钢丝绳AB上各弧段张拉力的水平分力相等，令水平分力恒等于常数SH0，则有

据平面力系的平衡条件∑Y=0，得

又SV2=SV1+dSV1，分离变量换算得

弧长元素段M点处的斜率

对式(3)求导得

将式(3)、式(4)代入式(2)得

联立式(1)、式(3)和式(5)得

进行二次积分

当边界约束条件x=0时，则y=0，代入式(6)得

当边界约束条件x=l时，则y=h，代入式(6)有

将C1、C2代入式(6)，得到钢丝绳的抛物线线形方程

静力平衡条件下钢丝绳的抛物线线形方程最终变换为

2.2 钢丝绳的张拉力

钢丝绳的抛物线线形方程确定后，钢丝绳各节点处的张拉力为

对式(7)求导，得

将式(9)代入式(8)，当x=0时，则钢丝绳在A节点处的张拉力为

将式(9)代入式(8)，当x=l时，则钢丝绳在B节点处的张拉力为

2.3 钢丝绳的挠度方程

沿水平轴x方向抛物线上的任意点至AB弦线上相应点的竖向距离，即挠度为

经过整理，得到静态平衡条件下钢丝绳的挠度曲线方程

令f'(x)=0，得极值点为x=l/2，即跨中挠度最大，代入f(x)得到钢丝绳最大挠度fMAX与水平跨度l的函数关系

2.4 钢丝绳的弧长方程

联立式(9)、式(10)得

弧长元素

取其中前3项并代入式(11)，积分得到[0，l]上的线形近似长度

进一步简化并忽略弹性伸长，得到钢丝绳的弧长方程为

3 空钩下降条件

浮式起重机电控系统通常按照梯形速度时间曲线对启、制动阶段的加减、速时间以及稳定的运行速度进行给定或控制，可根据功能需求和作业过程进行实时调整。电动机的转速按曲线中设定的规律实现增长或降低以满足负载升降作业时的各项性能指标要求，启、制动过程中速度与时间呈线性关系，加速度对时间的函数为a(t)=dv(t)/dt。起升减速制动和下降加速启动过程中的加、减速度为常数，平稳升降运行过程中加（减）速度为零。按该类型曲线运行的效率高，能够在较短的时间内完成加、减速过程，且对执行机构功率及作业循环时间等而言是具有优势的[13-16]。

吊钩组在空载或负载条件下的起升、下降运动过程是通过起升卷筒收绳或放绳来实现的，整个作业循环过程大致分为6个阶段。如图3所示，起升加速阶段oa、起升匀速阶段ab、起升减速阶段bc、下降加速阶段de、下降匀速阶段ef和下降减速阶段fg。在不同的运行阶段，速度的变化会引起各分支钢丝绳载荷的变化。

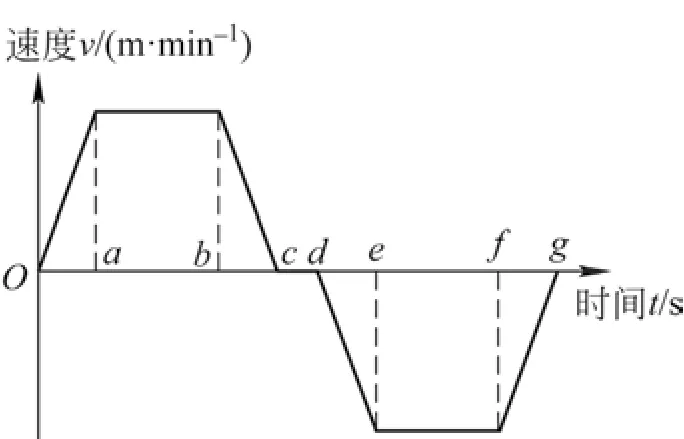
图3 速度与时间波形曲线

忽略系统刚度及惯性效应的影响，起升减速停车阶段，负载通过电气制动实现线性减速，平稳降至接近至零速后，进行无磨损机械抱闸停车，此时钢丝绳处于张紧状态。进入下降加速启动阶段时，制动器打开，PLC向变频器发送速度指令，卷筒开始放绳。放绳过程中，钢丝绳挠跨比ξ逐渐增加并趋于松弛，受力状态及线形特征不断发生着变化。

当空钩自重G0足以克服悬垂段钢丝绳末端张拉力SB、滑轮轴承静摩擦阻力fM及钢丝绳僵性阻力FJ等，即达到空钩下降的临界条件时，吊钩组便可开始下降。

臂架增、减幅过程中做变速运动，计算较复杂，亦会影响钢丝绳的受力状态和线性特征，但总体看对整体影响较小，此处暂不展开讨论。

4 空钩下降能力分析

基于定量分析和研究的需要，将起升减速制动和下降加速启动2种状态模式下进行转换时悬垂段钢丝绳弧长的差值，即起升卷筒放绳量ΔLp、放绳时间Δt作为空钩下降能力及下放作业效率的衡量标准，以实例进行分析其与关联参变量的关系。

图4为3 600 t双臂架浮式起重机主起升缠绕系统的总体布置型式。2个臂架沿船宽方向呈左右布置，整机额定起重量为2×1 800 t=3 600 t。单臂架上2个主钩沿臂架长度方向呈前后布置，额定起重量2×900 t=1800 t，单个主钩额定起重量为900 t。

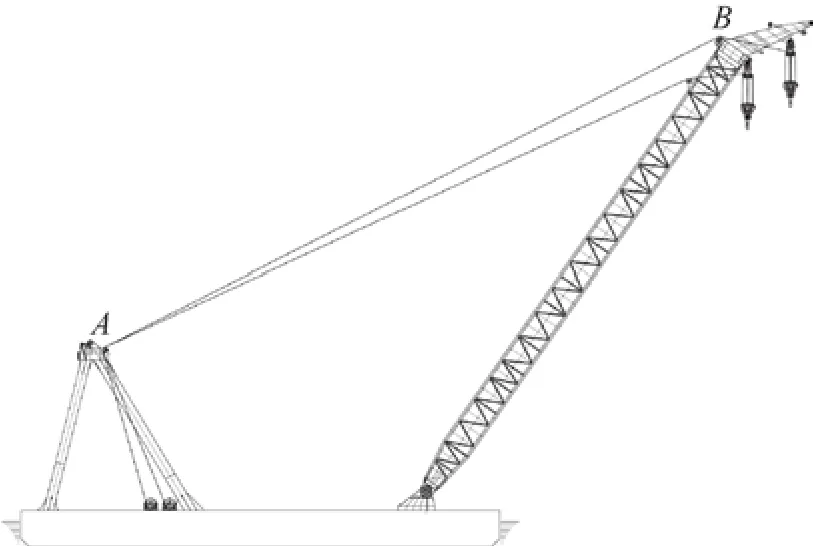
图4 主起升缠绕系统总体布置型式

以前主钩为例，A、B点分别为人字架及臂架上导向滑轮的旋转中心位置，技术参数如表1所示。

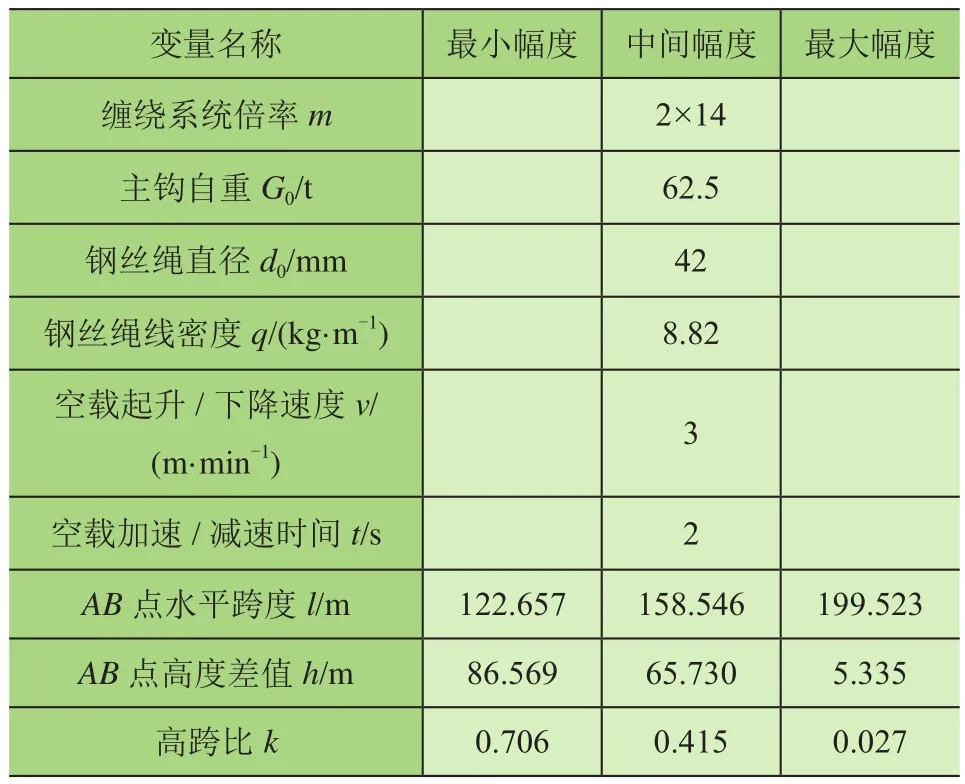
表1 主要技术参数

4.1 空钩下降前后挠跨比ξ的变化特征

电动机驱动卷筒实现吊钩组的升、降运行以及在各运行状态间进行过渡转化的过程中，悬垂段起升钢丝绳AB可通过自身几何形状的调整，达到与当前运行状态相适应的一种新的平衡状态，以消除这种由于跨度条件、运行状态等各种因素的变化而造成的体系不平衡。挠跨比ξ是悬垂段钢丝绳几何形状及内力的重要参数，是较直接的表征方式。如图5所示，全跨度范围内，空钩下降前和开始下降后挠跨比ξ的总体走势相似，随着水平跨度l的增加均呈下降趋势。同类运行状态下，负载及阻力的大小和作用方向保持不变，钢丝绳挠度发生变化以协调并适应跨度的改变。2种状态作比较，负载或阻力的大小及作用方向各异，同跨度位置的挠跨比ξ相差约5%，反映出空钩下降前后悬垂段钢丝绳几何形状的较大差异。

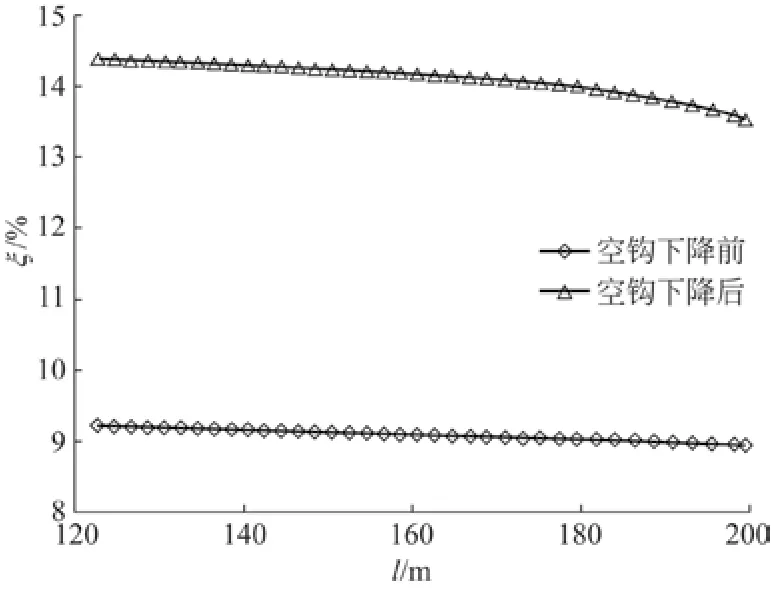
图5 挠跨比ξ的变化特征

4.2 张拉力SB与挠跨比ξ的关系

假定悬垂段钢丝绳B端固定，即认为卷筒放绳过程中吊钩组不上升也不下降，不受钩重、摩擦及僵性阻力等外部载荷的影响。分析3种典型幅度对应的水平跨度下，悬垂段钢丝绳末端张拉力SB随挠跨比ξ的变化趋势。

如图6所示，3种典型跨度数据下得到的曲线走势具有较好的一致性。不同水平跨度l条件下，当挠跨比ξ无限接近于0时，悬垂段钢丝绳末端张拉力SB均趋于无穷大。随着ξ的增加，SB起初急剧下降，随后下降趋势逐渐减缓。当ξ超过10%时，SB-ξ曲线近似趋于平坦。相同水平跨度l条件下，钢丝绳末端张拉力SB与挠跨比ξ成反比，ξ越小，SB也越大。

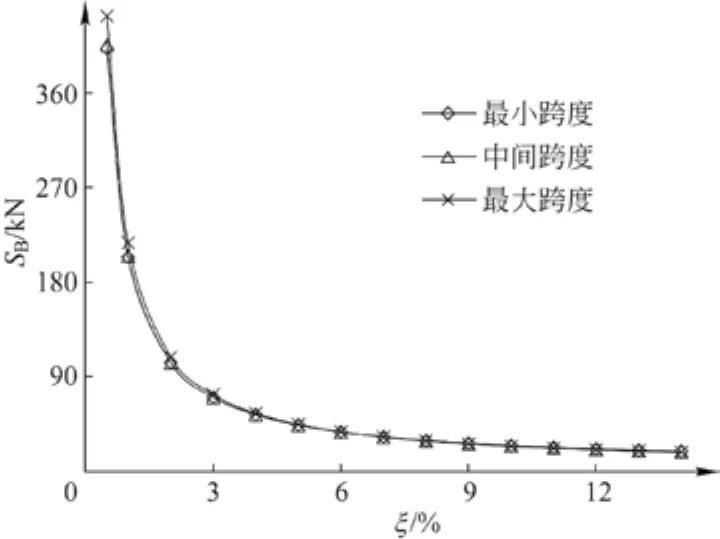
图6 张拉力SB的变化趋势

4.3 空钩自重G0的影响

单个主钩实际自重62.50 t，设计自重48.70 t （不含配重）。按照等差规律对主钩自重G0赋以不同的数值，得到各跨度下空钩下降所需放绳量的变化趋势。

由图7可知，相同钩重条件下，ΔLp随l的增大而增加。在趋近最大跨度位置即锚泊维护工况（k=0.027）时，ΔLp增势放缓，在较小钩重条件下，还伴有下降趋势。不同钩重条件下，空钩自重G0与放绳量ΔLp成反比。

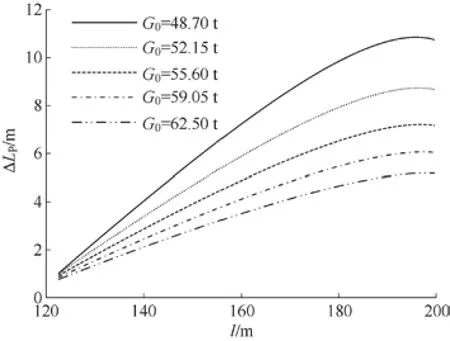
图7 空钩自重G0影响下放绳量的变化趋势

4.4 钢丝绳线密度q的影响

如表2所示，对钢丝绳线密度q赋以不同的数值，其余主参数不变。鉴于应用实践与数据分析比较的需要，求取满载工况钢丝绳的最大静张力并对钢丝绳分别予以选型，所有规格钢丝绳破断负荷的安全系数既不>5也不<3，满足规范设计要求[17]。

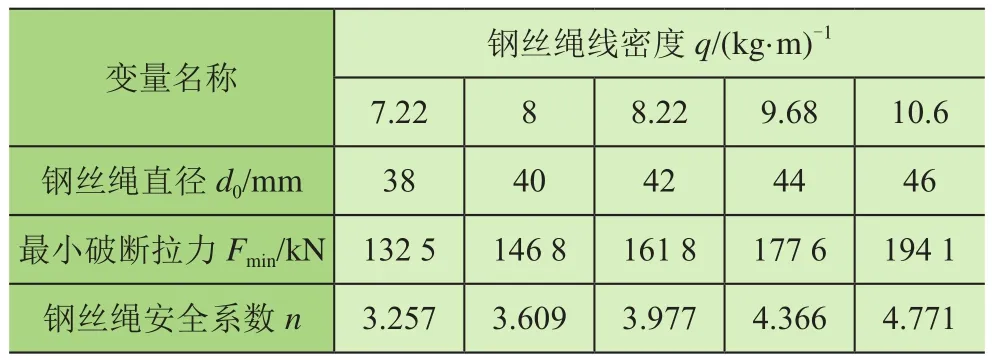
表2 不同线密度方案的参数设计

由图8可知，在全跨度范围内，放绳量ΔLp随着l的增加均呈增长趋势。在趋近最大跨度位置，增加幅度开始收缓。不同线密度条件下，放绳量ΔLp与线密度q成正比关系。

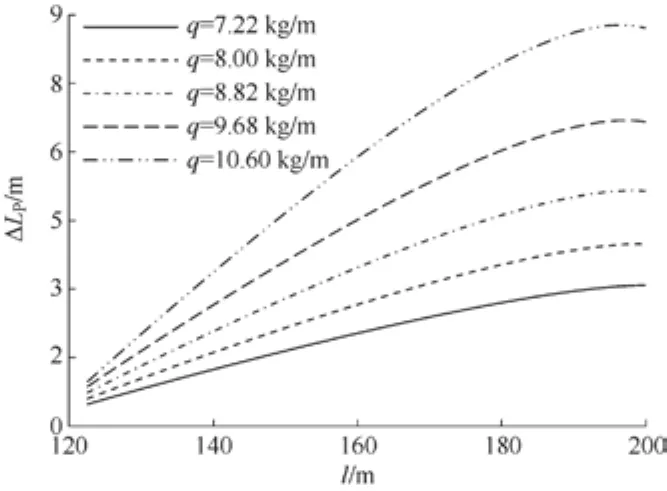
图8 钢丝绳线密度q影响下放绳量的变化趋势

4.5 速度曲线的影响

整机控制电源复位后，通过操作台的主令手柄来控制起升的运行方向及速度给定，起升驱动系统将以最大设定能力来完成加速或减速过程，以达到主令手柄所要求的速度。结合图3对吊钩组空载条件下的性能指标赋以不同的参数，考查其对空钩下降能力的影响。

如表3所示，曲线Ⅰ和Ⅱ的加、减速度a相同，稳定运行速度v不同。曲线Ⅱ和Ⅲ的稳定运行速度v相同，仅调整加、减速时间t以获得不同的加、减速度a。曲线Ⅰ和Ⅲ的各项性能指标均不同。

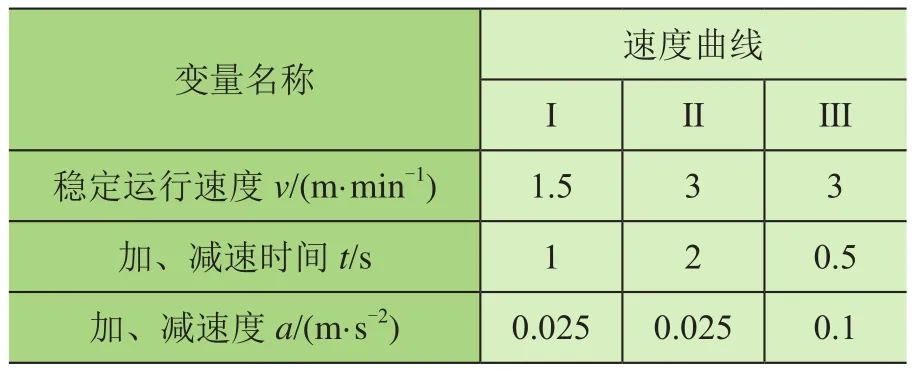
表3 不同速度曲线下的性能指标

由图9可知，在全跨度范围内，放绳量ΔLp随着l的增加均呈增长趋势。其中曲线Ⅲ的放绳量最大，而曲线Ⅰ和曲线Ⅱ却彼此重合，说明ΔLp与加、减速度a有关且成正比关系。但3类速度曲线在不同水平跨度位置的放绳量差距并不显著，曲线Ⅲ的加、减速度a是曲线Ⅰ、Ⅱ的4倍，最大放绳量ΔLp却仅为1.022倍，故可认为ΔLp对加、减速度a的变化并不敏感。

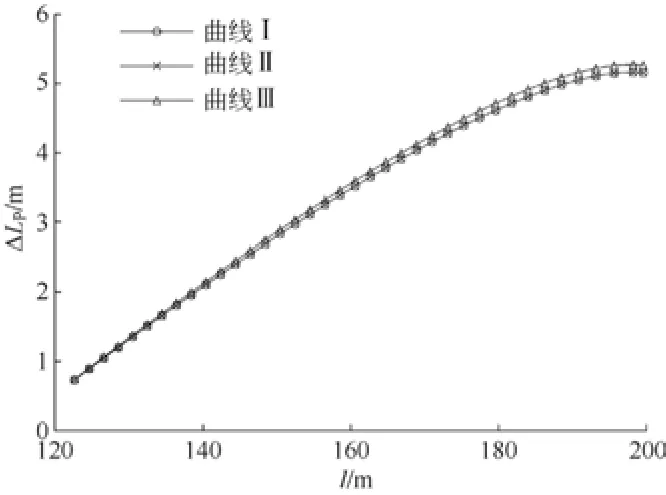
图9 速度曲线影响下放绳量的变化趋势

由图10可知，3类速度曲线的放绳时间Δt随着l的增加均呈增长趋势。曲线Ⅰ的增长速率始终高于曲线Ⅱ和曲线Ⅲ，而曲线Ⅱ和曲线Ⅲ的增长速率相近且保持相对稳定。当接近最大跨度位置时，增长速率趋于停滞。

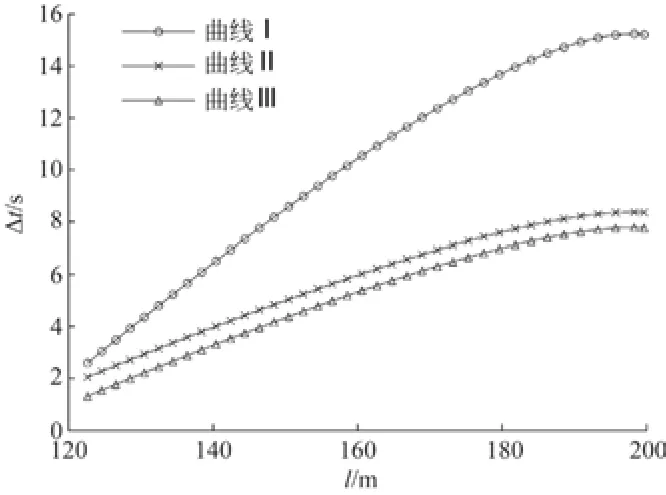
图10 速度曲线影响下放绳时间的变化趋势

5 结论

1)本文分析各跨度下的SB-ξ曲线，当挠跨比ξ不大时，其微小的变化量Δξ将引起悬垂钢丝绳末端张拉力SB的显著变化，反之则变化甚微。说明ξ较大时，通过卷筒不断放绳来增加ξ以降低SB的方法对空钩下降能力的提升作用已不明显。

2)相同钩重G0或相同线密度q条件下，大跨度位置下卷筒放绳量ΔLp较之小跨度位置明显增加，说明在大跨度位置时的空钩下降能力是相对较弱的。以该位置下的相关参数变量作为空钩自重设计的基础输入条件是较为合理的，其结果必然也满足小跨度位置下的使用要求，且大跨度位置高跨比k值较小，工程计算精度易于得到保证。

3)不同钩重G0或不同线密度q条件下，卷筒放绳量ΔLp随着跨度l的增加而呈现出相同的增长趋势，但数值上有差异。G0越大，则ΔLp越小，所需放绳时间Δt会越短，空钩下降能力越强。q越小，ΔLp越小，所需放绳时间Δt也越短，空钩下降能力越强。

4)相同加、减速度a条件下，放绳时间Δt与稳定运行速度v成反比，v越大所需放绳时间Δt越短，空钩下降能力越强。稳定运行速度v相同的条件下，放绳时间Δt与加、减速度a成反比，a越大ΔLp越小，空钩下降能力越强。与加、减速度a相比，提高稳定运行速度v对缩短放绳时间Δt的作用更显著。

研究结果考虑了起升速度控制技术的基本原理，并将定性的指标做了定量化处理，直观呈现了影响空钩下降能力的主要变量及其相互关系，分析所达到的效果并得到了空钩自重设计的合理输入条件，为工程技术人员理解、认识、应对及解决工程实践中的空钩下放等问题提供有益的参考。