基于四元数的轴承载荷分布求解方法

2023-03-27孙芳斌程红梁凌维安

科技创新与应用 2023年8期

孙芳斌，程红梁，凌维安

（1.南京航空航天大学，南京 210016；2.博世华域转向系统有限公司南京分公司，南京 210033）

轴承的载荷分布主要研究轴承变形与承载能力的关系，其中变形主要为滚动体接触变形及由此产生的内外圈相对变形，承载能力则是滚动体受载、轴承整体外载荷等[1]。轴承载荷分布直接关系着轴承的疲劳性能，只有确定了载荷分布才能够研究一些轴承的性能参数，如刚度、变形和接触应力等[2]。由于有限元的发展，轴承接触变形、接触应力可以通过商业软件很好地求解[3]，载荷分布求解十分容易；但有限元计算前处理耗时较多，理论方法仍是不可或缺的。

经典的低速轴承载荷分布求解基于赫兹接触理论得到滚珠——滚道挤压变形和压力的函数关系，通过轴承内外圈相对变形来描述滚珠挤压[4-7]。但涉及轴承内外钢圈的相对倾转，普遍做法是在某一平面内对转动分解到挤压接触点上，例如路春雨等[8]研究的四点接触高速轴承的力学模型，陈龙等[9]研究的四点接触球转盘轴承力学模型等。实际上除了轴承，其他的回转件如滚珠丝杠副也采用将倾转变形通过复杂的三角函数变换到接触点上去，求解滚珠的挤压变形量[10-11]。此类方法思路直观，但推导过程复杂，使用起来并不方便。四元数作为一种可以描述向量空间旋转的工具常被用于计算机几何图形学中[12-13]，其矩阵形式使用更是方便。周江华等[14]对四元数在刚体姿态仿真中的应用进行了分析。王思鹏等[15]应用四元数描述无人机姿态，实现了惯性测量单元信息与单目视觉信息融合以及无人机位姿态修正。董贵荣等[16]则是基于四元数实现复杂障碍物场景下对机器人位姿的精确控制，简化工业机器人逆运动学的求解过程。

为简化倾转变形的处理，本文将四元数应用于角接触球轴承相对变形中的倾转部分的描述，通过滚道圆弧曲率中心参数曲线的刚体位移量推导滚珠挤压变形，基于牛顿-拉夫逊方法求解滚珠载荷分布。算法可以轻易实现对各类球轴承的拓展，且对各种复合外载荷都能有效求解载荷分布。

1 载荷分布模型

1.1 四元数简介

四元数由1 个实数单位和3 个虚数单位组成，任意四元数可以写作如下形式

其中虚数单位满足

四元数也可以根据实部和虚部写作

对于一个四元数q，它的共轭四元数记为q*

如果一个四元数实部为0，则称这个四元数为纯四元数。对于一个空间向量v1，可以表示为纯四元数v1=[0，v1]。四元数运算可以表示向量的空间旋转，假设空间向量v1绕单位向量u 右手坐标方向旋转了θ 度后变为v2，对应的四元数v1经旋转后表示为v2，则对应的四元数运算可表示为

式中：v2=[0，v2]，旋转后仍是纯四元数。q 为对应旋转方向的单位四元数，q*为q 的共轭，此时q 计算式为

上述关系对应四元数的计算，在实际使用中为方便起见一般使用其矩阵形式，令

式中：θ 为绕单位向量u 转动的角度，[ux，uy，uz]T为单位向量u 的3 个方向的分量。则转动矩阵可表示为

对应向量旋转空间转动可以表示为

如图1 所示，空间转动对应的四元数不是唯一的，对于任意向量，绕u 方向旋转θ 角和绕-u 方向旋转2π-θ 角所进行的变换是完全一致的。

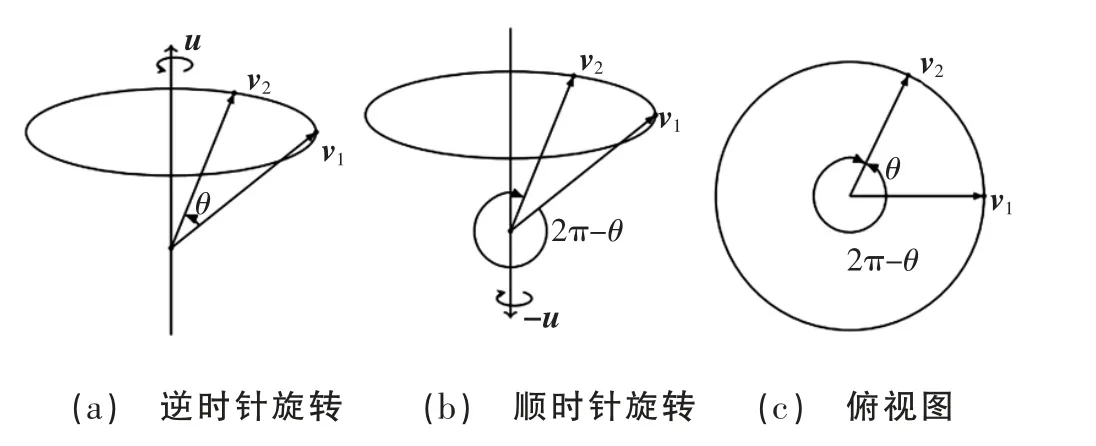
图1 向量旋转示意

1.2 接触变形求载荷分布

角接触球轴承由于接触角非零，相比深沟球轴承可以承受更复杂的外载荷，包括轴向力、径向力、倾覆力矩及上述的复合等。现对轴承分析做出如下假设：①滚珠与滚道的接触变形处于弹性范围内，满足赫兹接触假设；②变形前后两侧滚道的曲率中心与滚珠中心总是位于同一直线上（轴承转速处于低速情况）；③忽略滚珠滚道间摩擦力。基于以上假设，变形可以简化为内外圈滚道之间的相对变形，在分析时一般假设轴承外圈固定、内圈相对外圈有相对位移。

对于无外载荷时的理想滚珠运动运动路径曲线定义为L0，L0的参数曲线表达式

式中：R0表示轴承的节圆半径，将节圆定义在xoy 平面后，滚道圆心（曲梁中心）曲线偏离xoy 平面。滚珠半径为rb，外滚道半径为re，内圈滚道半径为ri，设计接触角为β0。

式中：R1为外圈滚道参数圆曲线的半径，R2为内圈滚道参数圆曲线的半径。

四点角接触球轴承的外圈滚道对应的2 条圆心参数曲线

四点角接触球轴承的内圈滚道对应的两条圆心参数曲线

对于四点接触球轴承，内圈和外圈各有2 条参数曲线，上标in/out 表明内外圈，下标L/R 表明参数曲线对应滚道小圆弧指向圆心的左右，而非参数曲线本身相对的左右位置。四点接触球轴承内外圈滚道之间由于受外载发生相对位移，可划分为绕xoy 平面内某一方向的转动和3 个平动分量。转动方向定义在xoy平面内，转轴角为φ，转动角度为θ，则对应转动四元数

滚珠受到滚道挤压产生的变形量由变形前后的参数曲线间距离变化决定，变形前滚道参数线距离为

变形后对应某一滚珠，滚道参数线接触点距离变为

式中：ti表示第i 个滚珠球心在参数曲线上的参数值，则表示发生相对位移后滚珠对应的内滚道参数取值，有

挤压受力方向

式中：cart2pol（）表示将笛卡尔坐标转化为极坐标的弧度参数，norm（）表示将向量单位化处理。由于实际滚珠变形受压，接触变形量不能够为负数，所以有

基于赫兹接触理论，接触变形与接触载荷的关系表示为

K 的计算与赫兹接触点处的主曲率和、轴承材料的弹性模量等参数相关。对受力、力矩向3 个主方向上分解，可以得到

式中：N 为滚珠总个数，i 为滚珠编号，Li1，Li2分别为外圈接触点到坐标原点距离，对于四点接触球轴承，有

轴承受到复合外载荷时（同时包含轴力、径向力和倾覆力矩），可以通过牛顿迭代法求解。已知复合外载荷F0=[Fx0，Fy0，Fz0，Mx0，My0]T，相对位移量δ=[δx，δy，δz，φ，θ]T，φ 为转轴角，θ 为转动角，通过迭代控制相对位移量使外载荷等于滚珠合力、合力矩。牛顿迭代需要求残差梯度，求导函数复杂，因此使用数值求导代替。需要注意的是，滚珠和力矩只需要取前2 项，第三项绕Z 轴为轴承扭矩，但分析过程并未考虑摩擦力，求出的摩擦扭矩并无参考价值。

上述分析过程可以表示为如下标准化流程。

1）列出轴承内外圈相对位移量δ=[δx，δy，δz，φ，θ]T。

2）列出轴承内外圈的变形前滚道圆弧圆心（曲率中心）参数曲线。

3）根据位移量生成旋转矩阵和平动位移向量，计算变形后的内圈参数曲线，外圈不变。

4）变形后内圈接触点不动，计算接触点到外圈斜对应参数曲线的距离，此距离减去变形前的距离即为滚珠变形压缩量，计算滚珠受载角度。

5）根据赫兹接触计算滚珠挤压力，将所有滚珠挤压力分解得到合力、合力矩。

对步骤1）—5）应用牛顿-拉夫逊方法，迭代求解相对位移量，并对应求出所有滚珠的载荷。

对于其他类型的球轴承，可以根据轴承的实际结构修改步骤2）中的参数曲线，但要注意步骤4）中内外参数曲线的一一对应关系也要相应做出修改。

2 算例分析

2.1 单列轴承

对上述模型进行验证，以某型号四点接触球轴承为例计算，其中轴承参数见表1。

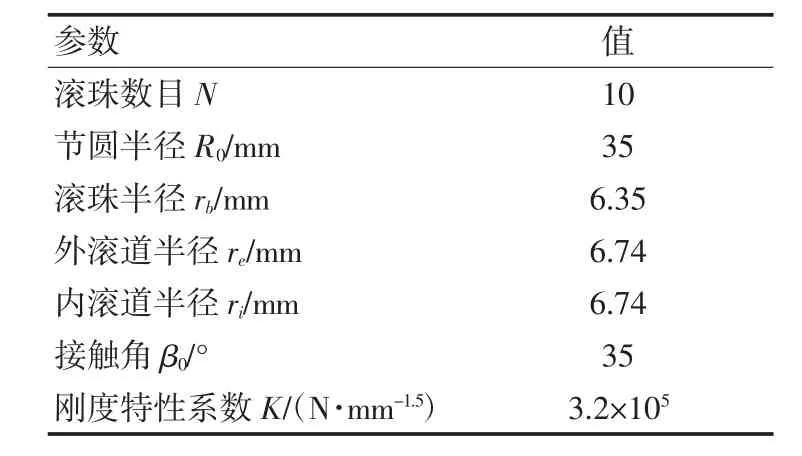
表1 轴承参数

考虑轴承所受外载荷类型差异，角接触球轴承可能同时承受径向力、轴向力和倾覆力矩，且受力/力矩的方向有所区别。分别按照不同外载荷类型搭配，并依据各种载荷类型搭配划分工况1—5，其中工况1—3为单一轴向力、径向力和倾覆力矩，工况4 为侧向力+倾覆力矩，工况5 为轴向力+径向力+倾覆力矩，具体各工况载荷所占比例见表2。根据如图2 所示的载荷方向，计算得到轴承外载荷分布如图3 所示。

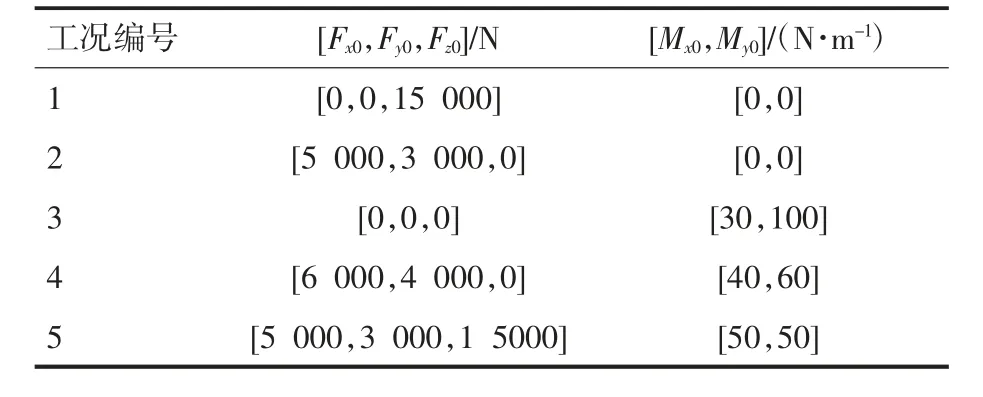
表2 工况载荷数据

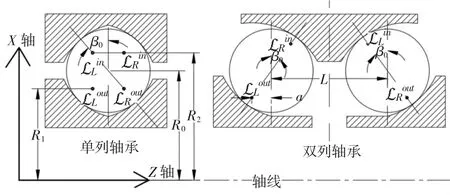
图2 轴承坐标系定义及参数示意

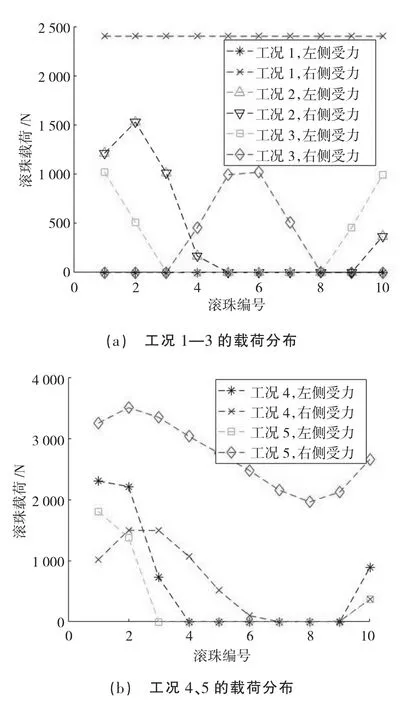
图3 单列轴承不同工况下滚珠载荷分布

表2 的5 种工况表示受载情况逐渐复杂，对于四点接触球轴承，在低转速情况下不同的使用场景5 种工况都有可能出现，最复杂使用场景下会出现同时承载3 种载荷的情况。图3 显示了5 种工况载荷取表2所罗列的数值时的轴承滚珠的载荷分布，其中滚珠载荷以外圈滚道为参考对象，分别绘制了滚道左右两侧与滚珠接触点的受力；滚珠编号则是按照xoy 平面内以x 轴为起点逆时针方向编排。工况1 表示对轴承施加纯轴向载荷15000 N，此时轴承只有右侧单边受力，且每个滚珠受力完全相等，这与定性分析的结论是完全一致的。工况2 对轴承施加的是纯径向载荷，可以看到此时单个滚珠左右2 边受到完全均等的挤压力，但不同滚珠受力会发生变化，所有滚珠合力作用下形成纯径向载荷。工况3 为轴承只受倾覆力矩载荷，此时滚珠两侧压力各不相同，综合之下产生了合力矩。

工况4、工况5 为复合载荷的滚珠载荷分布情况，由于载荷类型的叠加，滚珠载荷分布基本呈现无规律变化状态。工况4 为径向力+倾覆力矩，工况5 为轴向力+径向力+倾覆力矩，可以看到，外载荷越复杂，滚珠载荷峰值也越大。对比工况1 和工况5，增加径向力和倾覆力矩之后，滚珠承受的压力峰值从2400 N 增加到3503 N；工况2 和工况4 相比，增加倾覆力矩比纯径向力使滚珠压力峰值从1529 N 增加到2302 N。同时注意到，径向力和倾覆力矩也会造成滚珠载荷分布幅值（最大压力减去最小压力）的变化，从延长轴承寿命上来说，应该尽量避免这种情况。

2.2 双列轴承

相比于单列的四点接触轴承，双列轴承两列之间有列距L，只需要对载荷分布模型里参数曲线部分做些许修改，其余分析过程完全一致。如图2 所示中的双列轴承为例，参数曲线的x（t），y（t）部分不变，z（t）修改为

双列轴承列距L=20 mm，其余参数保持与表1 一致，计算得到该双列轴承的载荷分布如图4 所示，可以认为，复合载荷对双列轴承的载荷分布影响与对单列轴承的影响规律基本一致。此算例中的双列轴承参数曲线与单列轴承相比只有z 刻度上的差异，且单列轴承相当于列距L=0 的双列轴承。但是由于双列轴承列距非零，其滚珠载荷相对原点的力臂会增大，因此双列轴承在承担倾覆力矩后会与单列轴承的载荷分布产生细微差别。需要着重注意的是，此算例中使用的双列轴承每一列为两点接触，而单列轴承则是四点角接触轴承；对于更为复杂的四点接触双列轴承或多列轴承，都可以采取增加参数曲线或修改曲线参数等措施进行修正，而无需重新建立分析流程。