双馈风力发电系统的灵活虚拟同步发电机控制策略研究

王 磊，田 辉，牛俊杰，虎 军，张建盈

（宁夏银星能源股份有限公司，银川 750021）

风能因其广泛分别和可再生性的优势，已成为全球能源的重要组成部分[1]。双馈异步风力发电机组（DFIG）在并网时往往采用基于最大功率跟踪（MPPT）的恒功率控制策略，导致DFIG 的运行状态与风电并网系统频率完全解耦，使得DFIG 无法为系统提供有效的惯量和阻尼支撑[2]。当风电并网系统中有功负荷突变时，双馈风电系统频率的动态响应特性和稳定性受到了严重的威胁[3-4]。基于VSG 控制策略的DFIG 能够使其模拟同步发电机的运行外特性来增强风电并网系统频率响应能力。

近年来，利用VSG 控制策略解决双馈风电系统频率稳定性问题成为了研究热点[5]。Alpoor 等[6]提出了基于频率动态变化的灵活虚拟惯性控制策略，但该控制策略存在频率2 次跌落和DFIG 输出的功率的超调的问题。Wang 等[7]在DFIG 的转子侧控制器引入了惯性控制，使得DFIG 具有与同步发电机类似的静态频率调节性能，进而为系统提供频率支撑。高澈等[8]提出了一种基于和自适应虚拟转动惯量控制策略，以实现负载波动下的DFIG 精细控制。相比于实际同步发电机，VSG 控制策略的突出优势在于其控制算法中的转动惯量和阻尼系数均可以根据系统频率的变化及时灵活地进行调整，可显著提高系统频率稳定性[9-10]。

为改善分布式发电系统频率的稳定性，文献[11]改变了传统VSG 控制策略参数固定的缺陷，提出了棒-棒控制策略，即转动惯量在2 个固定的数值中变化，当系统频率的变化率小于设定阈值时，转动惯量取较小数值，否则取较大数值。虽然该控制策略在一定程度上克服了系统频率变化过快的缺陷，但该控制策略存在转动惯量变化范围过小的缺陷。Dong 等[12]、Ren 等[13]和Wang 等[14]分别采用了不同的灵活转动惯量控制策略以改善系统频率及分布式电源输出功率稳定性，但并未突出说明所采用的控制策略具有哪些优缺点。Karimi 等[15]在VSG 控制策略的基础上增加了模糊控制策略以有效地减小系统频率变化的最大幅值，进而防止频率越限。Li 等[16]提出了一种双灵活转动惯量控制策略，并根据不同的运行条件实现功率调节和频率调节的平衡，以优化系统的动态响应特性。与转动惯量恒定的VSG 控制策略相比，上述文献通过实时的灵活调整转动惯量可在一定程度上缓解系统频率的急剧变化，但转动惯量的调整不可避免地给系统带来了调整时间增加及分布式电源输出有功功率超调的问题。

为克服转动惯量的调整带来的不利影响，Xie 等[17]、Li 等[18]通过灵活调整阻尼系数抑制了系统频率变化，但并未精准地给出阻尼系数对于系统的影响，这对于分析VSG 控制策略参数对系统稳定性的影响来说是缺失的。Yao 等[19]在分析了转动惯量对于系统稳定性影响的基础上，采用了径向基函数（RBF）对转动惯量在线实时调整，并通过灵活调整阻尼系数以进一步抑制输出功率振荡，并增强了系统频率稳定性。但由于RBF函数的网络结构复杂，且隐层神经元数目庞大，因此所采用方法的运算时间可能会较长。Fei 等[20]以保持系统最佳阻尼比为目标，设计了一种灵活的转动惯量和阻尼系数。然而，所设计的灵活的转动惯量和阻尼系数仅能在小值和大值之间进行选择。Li 等[21]将暂态过程中的系统功角变化曲线划分为若干个区间，并根据转动惯量和阻尼系数在不同区间内所起作用设计了对应的灵活的转动惯量和阻尼系数。

基于以上的研究，构建了DFIG-EFVSG 并网系统模型，揭示了转动惯量、阻尼系数与系统频率偏差及其变化率之间的关系。并构建多种形式的EFVSG，分析了所提出的指数型EFVSG 在转动惯量和阻尼系数变化范围及抑制频率振荡的优势，在此基础上提出了一种指数型虚拟同步控制策略（EFVSG）以提高风电并网系统频率的稳定性。

1 DFIG 与EFVSG 控制策略数学模型建立

传统矢量控制策略的双馈风电机组，其功率输出与系统频率完全解耦。为使双馈风电机组具有更好的惯性特性，双馈风电机组的转子侧逆变器采用EFVSG控制策略作为外环，转子电流控制策略作为内环的双闭环控制策略。

1.1 EFVSG 控制策略的数学模型

EFVSG 控制策略分为有功功率-频率环和无功功率-电压环。当极对数p=1 时，借鉴同步发电机组的转子运动方程，其有功功率-频率环表示为

式中：Pm和Pe分别为EFVSG 控制策略的机械输入功率和电磁输入功率；Js 和DP分别为EFVSG 控制策略的阻尼系数和转动惯量，为更好地体现其与风电并网系统频率之间的关系，其具体的表达式将在第二节展现；ω0、ω 分别为额定角速度、EFVSG 控制策略中有功功率-频率环生成的角速度。式（1）中的Pm是由有功功率参考值P0和虚拟调速器输出共同组成，即

式中：P0为EFVSG 控制策略的有功功率参考值；KW为虚拟调节系数，取KW=P0/（0.01ω0），构成EFVSG 的一次调频环节。

根据同步发电机电压励磁调节方程，无功功率-电压环可表示为

式（3）中：E0、Es_m、E 分别为EFVSG 中无功功率-电压环的设定的额定电压的幅值、双馈风电机组定子电压幅值、EFVSG 控制策略中的无功功率-电压环生成的电压幅值；Dq为无功功率调压一次调节系数；Q0为EFVSG 控制策略中设定的无功功率参考值；Qe为输入到EFVSG 控制策略的无功功率；KP和Ki分别为EFVSG 控制策略中无功功率-电压环的比例、积分系数；Ta为延迟环节的时间常数。

1.2 DFIG 变流器控制策略的数学模型

为了得到DFIG 的转子电压的控制方程，定子电压在dq 坐标系中，取q 轴定向电压矢量，定子和转子的电压方程和磁链方程可表示为

式中：usd、usq、urd、urq分别为定、转子在dq 轴的电压；Rs和Rr分别为定、转子绕组的电阻；ωsl为转差角速度，即，ωsl=ωs-ωr；ωs、ωr分别为定、转子角速度；isd、isq、ird、irq分别为定、转子在dq 轴的电流；ψsd、ψsq、ψrd、ψrq分别为定、转子在dq 轴的磁链；Ls、Lr分别为定、转子绕组的自感；Lm为定、转子绕组间的互感。定子磁链和定子电压在忽略绕组电阻时可表示为

只考虑稳态项，结合式（6）和式（7）可得定子电压的方程为

结合式（4）到（6）可得转子电压控制方程

对dq 轴上产生的交叉耦合项采取前馈补偿控制策略，DFIG 的转子电流采用PI 调节器，得到转子电压的控制方程为

式中：Kpq、Kpd、Kiq、Kid分别为PI 调节器调节系数；为转子电流在dq 轴的指令值；urdc，urqc分别为转子控制电压在dq 轴的分量。

2 EFVSG 控制策略的分析

2.1 DFIG-EFVSG 风电并网系统的控制结构

以第一节数学模型为基础，本文提出一种以EFVSG 为外环，转子电流为内环的双闭环控制策略，DFIG-EFVSG 并网系统的控制结构如图1 所示。图1中EFVSG 控制策略中的无功功率-电压环输出的虚拟电流iabc_ref作为转子电流内环的参考电流，ird_ref和irq_ref分别为转子电流在dq 轴分量的参考值；ir_abc为转子电流；ird和irq分别为转子电流在dq 轴的分量；Δud和Δuq分别为转子电压在dq 轴分量的补偿项；ωr、θr、φs和ψs分别为转子角速度、转子相位、定子电压相位和磁链；ω，θ 分别为EFVSG 控制策略输出的角速度和相位；θsl2为转差相位，即θsl2=θ-θr；Esabc、Upcc、E 分别为定子电压、公共连接点（PCC）处的电压、EFVSG 控制策略产生的内电势的幅值；θ 和E 共同组成了EFVSG 控制策略产生的内电势Eabc；Rg、Xg分别为线路电阻和感抗；Rv和Xv分别为虚拟电阻和感抗。值得注意的是，本文应用超速矫正方法来校正原始最大功率点跟踪（MPPT）控制器中的最大功率曲线，从而得到校正后的最大功率点追踪控制器MPPT-MAR，这也降低了DFIG 以获得有功功率裕度。当转子速度ωr通过MPPT-MAR 控制器时，获得有功功率指令值P0。

图1 DFIG-EFVSG 风电并网系统的结构图

图1 中K/P 表示直角坐标系转换为极坐标系的过程，其定子磁链及电压补偿表达式分别为

式中：ωsl2为基于EFVSG 控制策略生成的转差角速度，即ωsl2=ω-ωr；usα、usβ分别为定子电压在αβ 轴的分量。

2.2 EFVSG 控制策略中转动惯量J 和阻尼系数Dp 表达式的建立

根据式（1）（2）可得基于VSG 控制策略的角速度偏差的变化率dΔω/dt 和角速度的偏差Δω 分别为

J0和DP0分别为转动惯量和阻尼系数的初始值，并且这2 个数值不随频率变化而变化。由式（13）可知，假定P0-Pe-（DP0ω0）Δω 不变，则随着J0的增大，dΔω/dt 减小，进而防止频率变化速率过快。而由式（14）可知，假定P0-Pe-J0ω0（dΔω/dt）不变，则随着Dp0的增加，Δω 减小，进而防止频率偏差过大。

在不改变J0和Dp0的基础上，通过调整J 和Dp能够使得VSG 控制策略中的J0和DP0分别等效地增加，以进一步抑制dΔω/dt 和Δω。由于风速改变会引起ωr改变，进而导致功率指令值P0发生改变，此时借鉴Fei等[20]将暂态过程中dΔω/dt 和Δω 的暂态振荡曲线划分为如图2 所示的4 个区间。

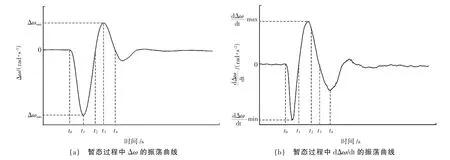
图2 暂态过程中Δω 和dΔω/dt 的振荡曲线

在第一、三区间t0-t1和t2-t3内，由于Δω 和dΔω/dt变化方向一致，故需要通过增大J 以进一步约束dΔω/dt，进而防止Δω 的进一步增大及Δω 的最大幅值ΔωAMP过早地到达，也能抑制频率的急速变化。而增大Dp虽然可以减小Δω，但会导致ΔωAMP过早地到达。因此，第一、三个区间的主要目的是让J 参与频率的调整，KIFLp保持不变。

在第二、四区间t1-t2和t3-t4内，由于Δω 和dΔω/dt变化方向相反，若通过增大J 参与频率的调整，则会抑制dΔω/dt，进而会对Δω 的恢复造成不利的影响。因此，在这2 个区间内，不宜增大J。由于Dp能够减小Δω，因此，第二、四区间的主要目的是让Dp参与频率调整，J 保持不变。J 和Dp的具体选取规则见表1。

表1 J 和Dp 的选取规则

本文提出的EFVSG 控制策略是在表1 的选取规则上衍生的。J 与dΔω/dt 构建起相应的函数关系，而Dp则与Δω 构建起相应的函数关系。此时，J 与Dp能够分别根据实时的dΔω/dt 与Δω 进行调整。由于J 与Dp均可灵活地调整，为更好地提升系统频率的稳定性，研究了以下3 种J 与Dp的表达式。

2.2.1 基于棒-棒控制思想的J 与Dp

基于棒-棒控制思想，J 与Dp的表达式如下

式中：Tj为|dΔω/dt|的阈值，且Tj>0。Td为|Δω|的阈值，且Td>0。为防止由于风速小范围变化时引起EFVSG 控制策略的频繁启动，因此设定|ΔPe|为Pe变化的绝对值，Pj为|ΔPe|的阈值。

2.2.2 反正切型J 与Dp

J 与Dp可以选择具有上下边界的反正切函数，使J与Dp可以在一定范围内变化。J 与Dp的表达式如下

式中：M1为反正切型J 中的控制参数，W1为反正切型Dp中的控制参数。当dΔω/dt、Δω 和ΔPe均超过设定的阈值时，J 与Dp分别根据dΔω/dt、Δω 以反正切函数的形式进行实时的灵活调整，进而提高频率的稳定性。

2.2.3 指数型J 与Dp

本文提出一种单调递增的指数型J 与Dp，使J 与Dp可以以指数函数的形式变化。J 与Dp的表达式如下

式中：M2、M3分别为指数型J 中的控制参数，W2、W3分别为指数型Dp中的控制参数。J 与Dp分别根据dΔω/dt、Δω 以指数函数的形式进行实时的灵活调整，进而分别抑制dΔω/dt、Δω。

2.3 指数型EFVSG 优势分析

相比于指数型EFVSG，棒－棒型EFVSG 的不足之处在于其只能分别对应的在2 个固定的数值J0和J1、Dp0和Dp1中切换，导致J 和Dp变化范围过小，故不能很好地应对变化多端的实际情况。同时当dΔω/dt、Δω过大时，由于指数型函数固有特点，J 与Dp会迅速增大以提升系统频率的稳定性。

3 EFVSG 控制策略的验证

为验证本文提出的指数型EFVSG 控制策略的优越性，其并网拓扑结构如图3 所示。图3 中DFIG 的转子侧控制器（RSC）采用反正切EFVSG 控制策略。同时，采用虚拟同步机控制策略的并网逆变器作为模拟电网的等效模型。

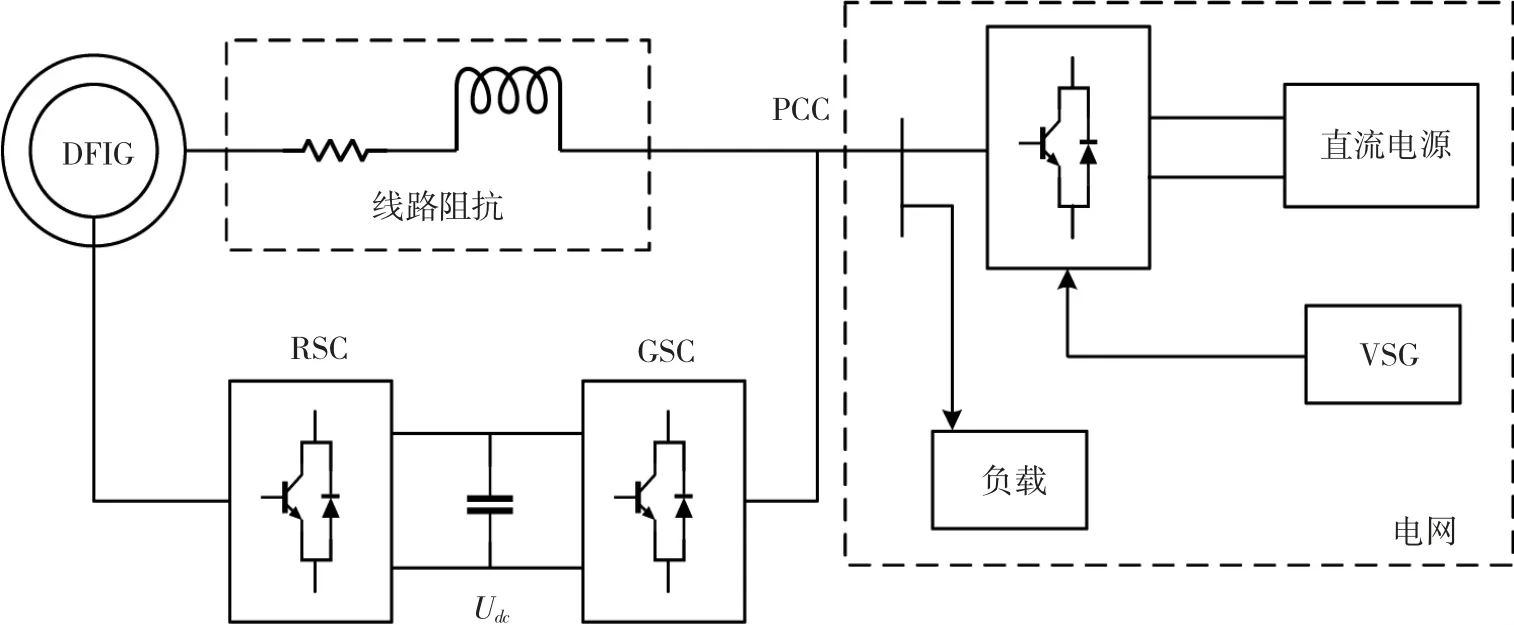
图3 DFIG-EFVSG 风电并网系统的仿真拓扑结构图

令DFIG 追踪超速运行点，使稳定状态下的DFIG 输出的有功功率由1.5 MW 调整为1.1 WM，即DFIG 获得备用容量0.5 MW。系统频率偏差允许范围在±0.5 Hz。同时设定在0～0.7 s 系统稳定运行，在0.7 s 时，功率指令值P0突增到1.275 MW。此时，观察系统频率动态响应和DFIG 输出有功功率的影响。

基于VSG 控制策略和EFVSG 控制策略的DFIG输出的有功功率及其频率对比结果如图4 所示。根据图4（a）可知，相比于VSG 控制策略，当dΔω/dt，Δω 和ΔPe均超出设定的阈值时，EFVSG 控制策略下的DFIG输出的有功功率超调量σ%更小，调整时间ts更少的优点。根据2.2 节分析可知Δω 在未到达第一个峰值时dΔω/dt 与Δω 方向一致，此时EFVSG 控制策略中M2和M3能够约束dΔω/dt，故基于EFVSG 控制策略的频率最高点低于VSG 控制策略频率最高点。EFVSG 控制策略中W2和W3能够减小Δω 的变化并增强系统的稳定性。图4（b）验证了理论分析的正确性及EFVSG 控制策略的优越性。2 种控制策略的σ%分别为8.835%、6.875%，ts分别为0.408 和0.342 s。

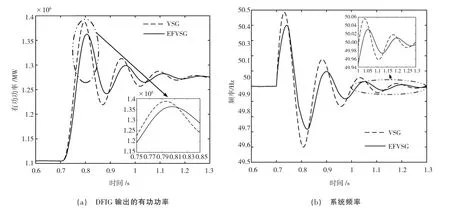
图4 基于VSG 和EFVSG 控制的有功功率和系统频率对比图

4 结论

本文在建立DFIG-VSG 并网系统基础上，详尽地分析了转动惯量、阻尼系数与风电并网系统频率之间相对应的关系，以揭示恒定参数VSG 存在的缺陷。在此基础上，建立了棒-棒、反正切、指数型EFVSG，通过对比分析得出了指数型EFVSG 的优势。最后通过仿真结果验证了指数型EFVSG 控制策略具有有效性及优越性。