防灾避险绿地可达性阻碍系数研究
——以四川长宁县中心城区为例
2023-03-27唐德富
唐德富
(中规院(北京)规划设计有限公司海南分公司,海口 570100)
可达性是指从一个点到达另一个点的难易程度。1959 年汉森(W.G.Hansen)首次提出“可达性”的概念,汉森最早将可达性运用于交通网络方面,可达性的评价与3 个因素有关:交通成本、区位吸引力、区位需求力[1]。本文在继承和学习现有理论基础和研究方法的同时,结合四川长宁6.0 级地震的现实情况,将可达性的影响因素转化为对阻碍系数的研究。
1 研究概况
2019 年6 月17 日,长宁发生6.0 级地震,震源深度16 km,震中心北纬28.34°,东经104.90°,震中距离长宁县中心城区约22 km。此次地震导致死亡13 人,重伤200 余人。宜宾市处于华蓥山基底大断裂南段,华蓥山基底断裂带长300 多km,以北东方向贯穿该市全境,控制着宜宾的地震活动。该基底大断裂带与西北向的雅安—峨眉—宜宾(江安-合江深大断裂和长宁—珙县—筠连—叙永)基底断裂带,形成深部基底断裂构造格局,构成宜宾潜在震源区。为此,省地震局将宜宾区域划为可能发生6.0 级地震风险的潜在震源区,如图1所示。
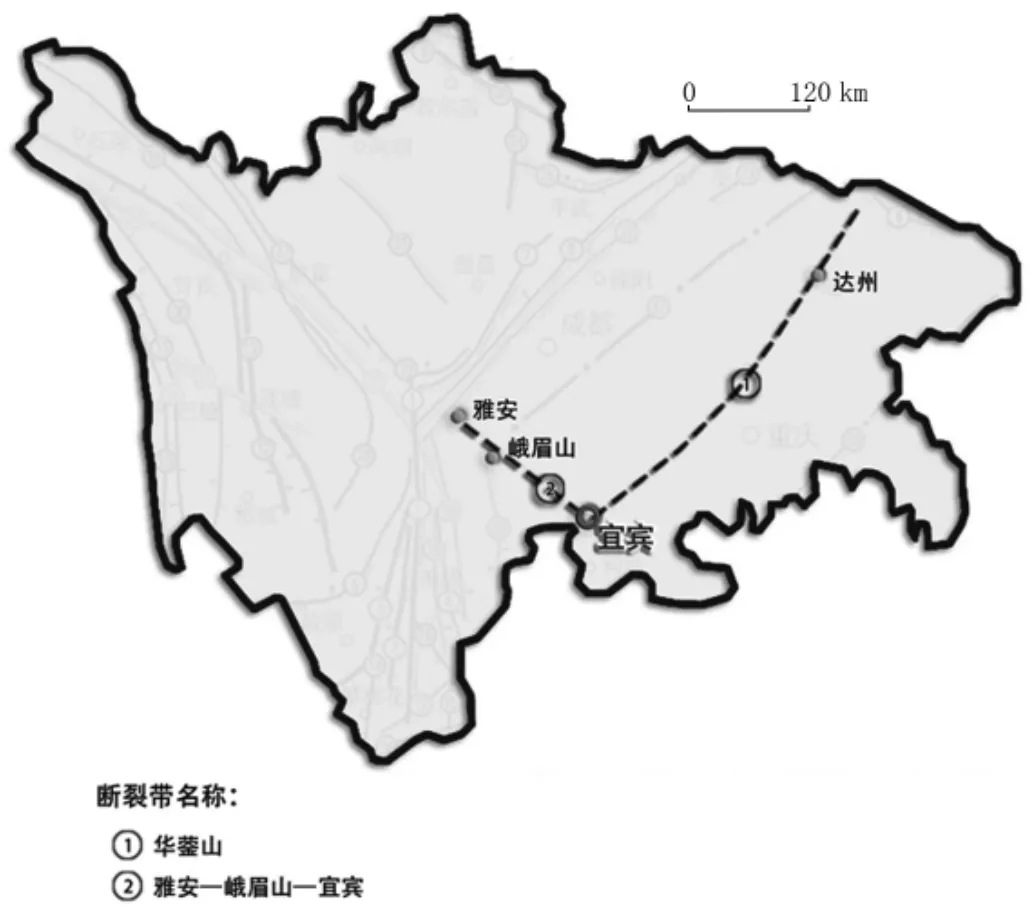
图1 四川省、重庆市断裂系统图
2 数据来源及研究方法
2.1 数据来源
本文研究区域涉及的中心城区边界、防灾避险绿地、人口、道路长度、宽度和坡度等相关数据来源于《长宁县城市总体规划》。街道路网格局、中心城区高程分析原始数据来自于2019 年高清卫星影像。通过GIS 地理配准工具将卫星影像图进行校正和相关数据矢量化处理,建立路网属性数据库。相关数据分析处理如图2~5 所示。
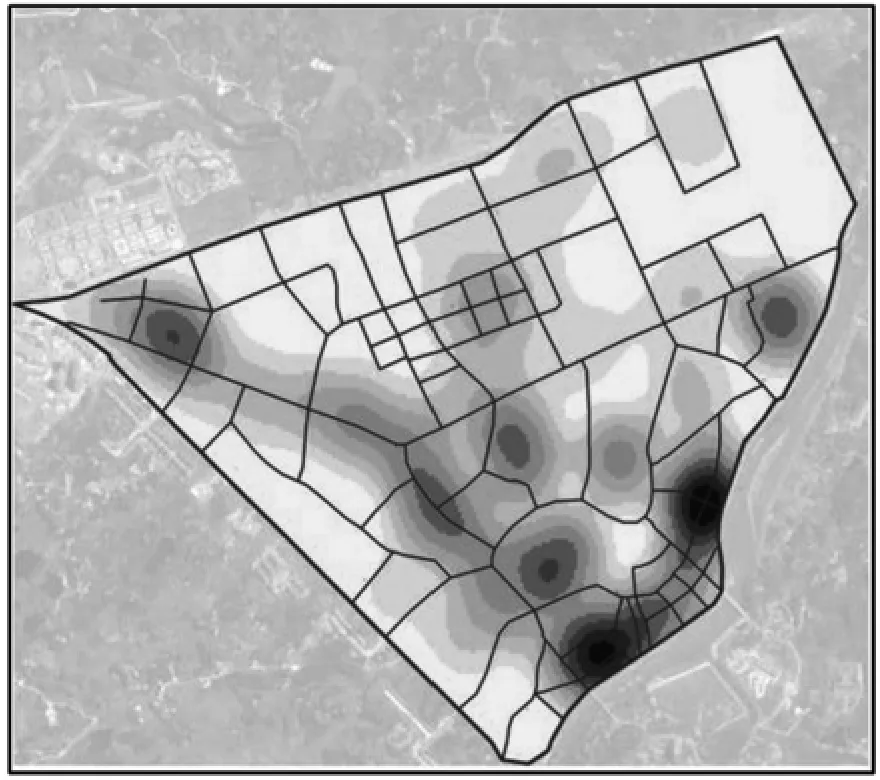
图2 人口密度分布图
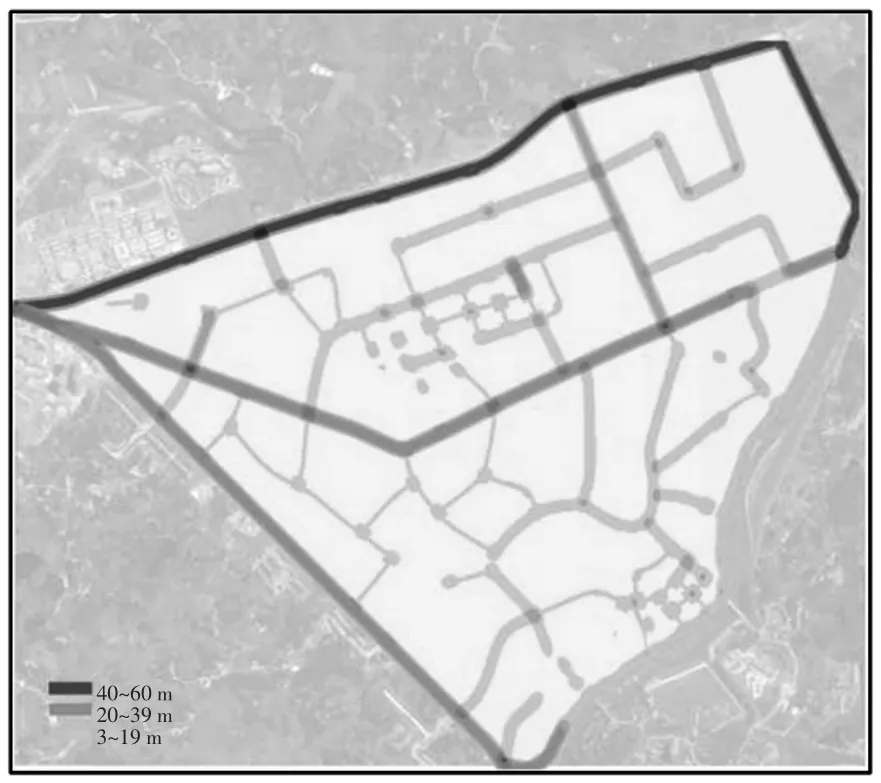
图3 道路宽度图
2.2 研究方法
2.2.1 最邻近距离法
最邻近距离法主要用于分析空间要素分布的集聚情况,也就是某要素在地理空间上相互临近程度的指标[2]。运用最邻近距离法测定点状要素与最邻近点的距离为ri,得到表征空间邻近程度的平均最邻近距离ri,公式为
式中:ri为平均最邻近距离;rE为理论最邻近距离;n 为防灾避险点要素数量;A 为研究区域面积;D 为点密度;R 为最邻近指数,即实际最邻近距离与理论最邻近距离的比值。通常情况下,当R>1 时呈现均匀分布状态,当R<1 时呈现集聚分布状态,当R=1 时呈现随机分布状态。

图4 道路坡度分布图
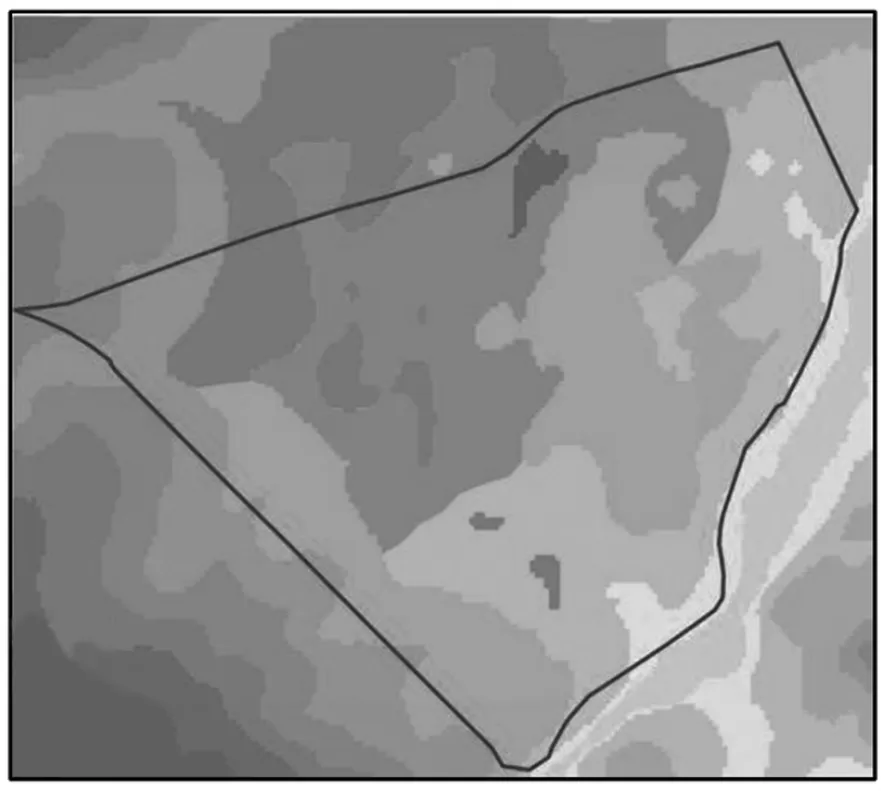
图5 中心城区高程分析图
2.2.2 核密度分析法
核密度分析认为某一事件可以在一定区域的地理位置发生,并且不同位置发生的次数不同[3]。此方法用于研究中心城区人口分布密度和防灾避险绿地的空间分布外,还用于以道路交叉口为节点,将阻碍公式赋值后分析路段的阻碍系数并进行可视化。公式为
式中:n 为事件在空间区域中发生的次数;hn为带宽,即搜索半径;为核函数。
2.2.3 线性回归分析法
通过相关实验数据分析,设变量y 与x 之间存在某种相关关系,其中x 是可控制的变量,y 是可预测的随机变量,变量x 可以影响变量y,但是变量x 不能完全决定变量y[4]。这时x 与y 之间不确定性的关系可以表示为
式中:x 代表自变量,y 代表因变量,回归模型f(x)描述了y 与x 的线性关系,即f(x)的回归函数。
3 可达性阻碍系数构建
3.1 道路长度阻碍因子模型建立
利用Spss 软件分析不同道路长度所需不同时间的统计数据。首先将实验分为4 个小组,每个小组5人,利用每个小组在同1 条道路的模拟实验值做线性相关分析。实验数据中取拟合优度R2的最大值,即R2=0.9781 为本次实验的最大值。R2越趋近于1 说明关于道路长度与避险速度的函数线性相关性越高,实验的精度越高(图6)。

图6 长度与速度的函数关系图
通过线性回归分析方法得到速度的函数表达式,再将道路长度比上速度之间的关系式,即为该条道路避险所需的理论时间。由于不同的城市有不同的街道尺度和不同的防灾避险绿地面积,因此将该理论值与最邻近指数R 的乘积作为道路长度的阻碍系数公式,公式为
式中:λα为道路长度阻碍系数;为连接交叉口i点到j 点的道路总长度;-0.0024+5.4091 为连接交叉口i 点到j 点的道路总长度与速度之间的函数关系式。
3.2 道路坡度阻碍因子模型建立
同理,在道路长度宽度相同且坡度不同的情况下做模拟实验,运用Spss 软件建立道路坡度与速度之间的线性关系式[5]。实验结果得到R2=0.9944,为本次实验的最大值。R2越趋近于1 说明关于道路坡度与避险速度的函数线性相关性越高,实验的精度越高。坡度与速度的函数关系如图7 所示。
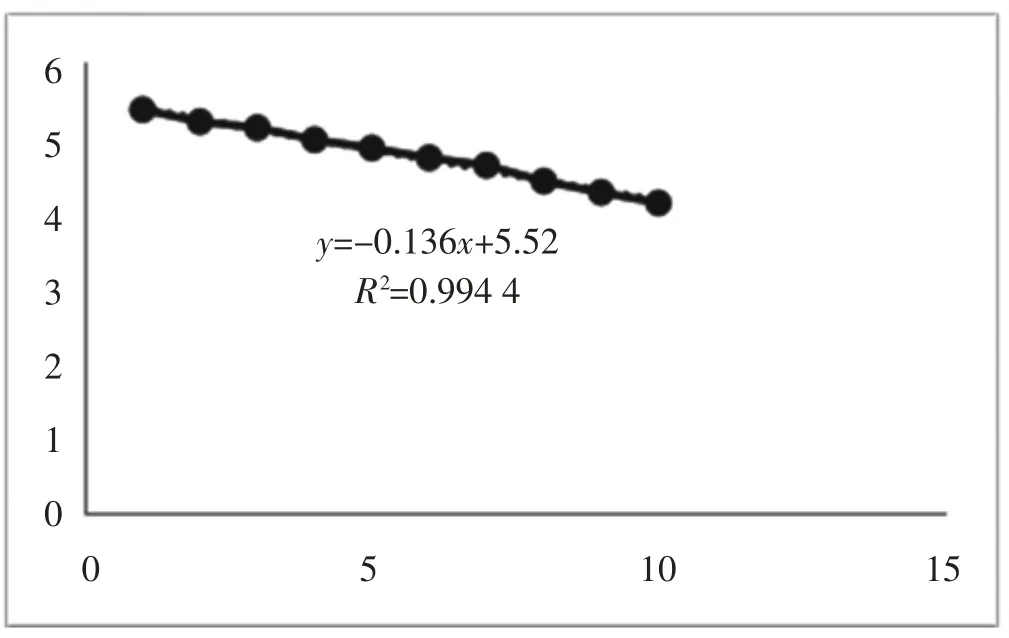
图7 坡度与速度的函数关系图
将道路长度假定为1,同理得出道路坡度阻碍系数公式
式中:λβ为道路坡度阻碍系数值;(-0.136Cij+5.52)为连接交叉口i 点到交叉口j 点道路坡度与速度之间的函数关系式。
3.3 道路宽度阻碍因子模型建立
实验过程发现当道路宽度越宽时对避险人员的容量越大,因此道路越畅通阻碍系数越小,反之阻碍系数越大。公式为
式中:λγ为道路宽度阻碍系数值;为服务人口与街道宽度之间的关系式,随着人口的增加道路承载力下降,阻碍系数增加,随着道路宽度的增加承载力上升,阻碍系数降低。P 为现状街道容纳人口的数量;Lij为连接交叉口i 到j 的道路长度;Wij为连接交叉口i 到j的道路宽度;Mij为连接交叉口i 点到交口j 点的道路权重值,用于解释连接交叉口i 点到交叉口j 点的道路到达防灾避险绿地的综合实力;Dij为连接交叉口i 点到j 点的道路与最邻近防灾避险绿地边界的距离。
4 结论与不足
4.1 结论
通过道路长度、道路宽度、道路坡度3 个因子的模型建立,分析不同影响因子之间的关系。由于各个影响因子之间相互独立且互不影响,因此由3 个影响因子相加得出防灾避险绿地可达性的阻碍系数公式
4.2 不足
本研究区选取防灾避险绿地为面积大于2000 m2的公园、绿地、广场,排除了面积较小的绿地广场和学校操场,研究结果可能会低估长宁县中心城区防灾避险绿地的可达性阻碍系数。另外,为降低防灾避险绿地可达性阻碍系数,规划过程中采取的方法仅为新增防灾避险绿地或连接断头路,由于中心城区的路网格局和城市形态基本定型,因此不考虑拓宽道路或降低坡度。
