新情境创设，新高考命题

施恂栋

摘 要：新情境创设及其应用问题，已经成为高考数学试卷命题的一个重要应用场景.结合情境的由来、活动以及类型等方面，就现实生活情境、科学研究情境以及劳动生活情境等加以实例剖析，引领并指导数学教学与学习，深化复习备考.

关键词：情境；高考；命题；现实生活；科学研究

1 情境由来

《普通高中数学课程标准（2017年版2020年修订）》中多次出现“情境”一词，《中国高考评价体系》规定了高考的考查载体——情境，以此承载考查内容，实现考查要求.《中国高考评价体系说明》对“情境”的定义，以及“情境”与“四层四翼”之间的关系作出了解释.

数学情境作为高考评价体系中的考查载体，成为高考数学试卷命题中的一个创新与应用场景，结合“四层”的渗透，“学科素养”的融合，指向“立德树人”，成为高考试卷命题中全面合理实现“价值引领、素养导向、能力为重、知识为基”的考查载体与阅读材料.

2 情境活动

“情境”在高考评价体系中的具体表现就是“问题情境”，通过现实生活中的问题来创设应用背景，借助问题或任务来合理构建数学模型，从而通过活动场景的创设来融入并渗透数学知识.

基于“问题情境”的创新性、复杂性与多变性，在高考评价体系中现实出现在试卷中的情境活动，往往可以具体表现为两个方面：

一个方面是简单的现实生活场景与应用情景.此类问题是基于现实生活中的某一场景与对应的知识点加以创设，通过情境分析与测评，合理构建相应的数学模型.

另一个方面是复杂的社会生活场景与应用情景.此类问题是基于社会生活中的一些复杂的生活问题，包括社会发展现状、数学文化与历史场景、科技前沿与科学应用等方方面面，借助数学模型的构建，综合考查数学基础知识与基本能力等.

3 情境类型

在实际的高考数学命题中，情境化试题更加灵活多变，以典型情境来合理创设，同时注意阅读理解的内容设置，合理有效控制文字阅读的数量与难度.在数学知识与情境联系上，合理设置巧妙的联系，过渡自然，衔接合理.数学模型的构建，以及对应的逻辑推理或数学运算的设置也比较合理，与学生的实际认知水平等方面具有较高的契合度，没有太偏或太难的场景，吻合大多数考生的实际能力水平与认知能力.

3.1 创设现实生活情境

现实生活情境的高考命题中，往往以贴近学生的生活、学习等场景来合理创设，具有较高的现实意义，对于研究与应用价值也比较高.在2023年的高考数学试卷中，就以现实生活情境中的滑冰和滑雪等冰雪运动、参加公益活动时的志愿者报名等来设置，接近生活实际，倡导学生进行运动锻炼以及志愿者活动，增强体质与社会责任感等.

例1 （2024届河南省天一联考高三（上）调研数学试卷）位于成都市龙泉驿区的东安湖体育公园是第31届世界大学生夏季运动会的核心场馆，它包含一座综合运动场、一座多功能体育馆、一座游泳跳水馆和一座综合小球馆.现安排包含甲、乙在内的6名同学到这4个场馆做志愿者，每人去1个场馆，每个场馆至少安排1个人，则甲、乙两人安排在相同场馆的方法种数为（  ）.

A. 96

B. 144

C. 240

D. 360

分析：根据志愿者活动安排，通过分组的分类讨论，结合排列组合的相关知识进行简单的计数与应用，进而确定相应的安排方法种数.

解析：先将6名同学分成4组：一种方式是甲、乙组成一组，再从另外4人任选2人组成一组，其余的一人一组；另一种方式是甲、乙与另外4人中的1人组成一组，其余的一人一组，再把4组人分到4个场馆.

所以安排方法种数为（C²₄+C¹₄）·A⁴₄=240，故选择答案：C.

3.2 设置科学研究情境

科学研究情境的高考命题中，往往以中国现阶段的科技与创造、社会热点的科技水平与能力等来合理创设，对于科学技术的认识、研究能力的判断等有一定的教育意义.在2023年的高考数学试卷中，就以科学研究情境中的臭氧环境对动物生长的影响、噪声污染与研究、医学中的漏诊率和误诊率的检测标准制度等加以合理创设，让学生认识一些现实生活不太经常接触的问题，从而借助科学研究的情境创设，合理引导学生树立热爱科学的理想信念，为我国社会主义事业的科技发展与社会建设努力学习基础知识.

例2 （2024届河北省保定市重点高中高三（上）学期开学数学试题）2015年5月，国务院印发《中国制造2025》，是我国由制造业大国转向制造业强国战略的行动纲领.经过多年的发展，我国制造业的水平有了很大的提高，出现了一批在国际上有影响的制造企业.我国的造船业、光伏产业、5G等已经在国际上处于领先地位，我国的精密制造也有了长足发展.已知某精密设备制造企业生产某种零件，根据长期检测结果，得知生产该零件的生产线的产品质量指标值服从正态分布N（64，100），且质量指标值在［54，84］内的零件称为优等品.

（1） 求该企业生产的零件为优等品的概率（结果精确到0.01）；

（2） 从该生产线生产的零件中随机抽取5件，随机变量X表示抽取的5件中优等品的个数，求X的分布列、数学期望和方差.

附：P（μ-σ≤X≤μ+σ）≈0.6827，P（μ-2σ≤X≤μ+2σ）≈0.9545，P（μ-3σ≤X≤μ+3σ）≈0.9973.

分析：（1） 根据创新情境，产品质量指标值服从正态分布N（64，100），结合3σ原则，求优等品的概率；（2） 确定随机变量X的取值，计算相应的概率，列出分布列，利用二项分布求数学期望和方差.

解析：（1） 依题，X～N（64，100），则μ=64，σ=10，54=μ-σ，84=μ+2σ.

由P（μ-σ≤X≤μ+σ）≈0.6827，P（μ-2σ≤X≤μ+2σ）≈0.9545，

由X～B（6，0.82），则有E（X）=5×0.82=4.1，D（X）=5×0.82×（1-0.82）=0.738.

3.3 设计劳动生产情境

劳动生产情境的高考命题中，以手工操作、技能训练等为问题场景来创设一些相应的试题，借此考查劳动生产的知识、技能与能力等.在2023年的高考数学试卷中，就以劳动生活情境中的橡胶生产工艺比较与应用、信号传输与概率等方面加以合理的创设，合理引导学生热爱劳动，优化效益，提升劳动生产能力等，努力学习基本知识，为报效祖国与报效人民奠定基础.

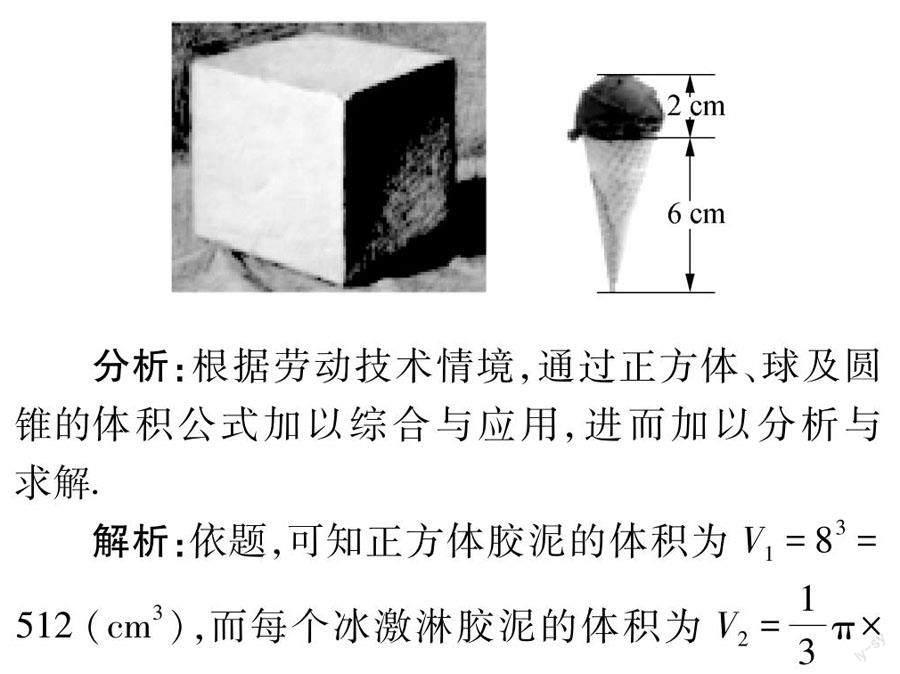
例3 （2023年湖南省益阳市高三（上）期末数学试卷）在一次劳动技术课上，某12人的小组中的同学们利用如图棱长为8cm的正方体胶泥作为原料，每人制作一个如图冰激淋胶泥模型（上部分为一个半球，下部分为一个以半球的大圆面为底的圆锥），则制作完成后剩下的胶泥约为（  ）.（忽略制作过程中的损耗，π≈3.14）

A. 8.7cm³

B. 9.6cm³

C. 10.6cm³

D. 12.4cm³

近年來高考数学试卷已经是“无情境不命题”了，高考数学试题合理融入创新问题情境与数学活动，让学生借助数学的基础知识与基本能力等来分析与解决具体的数学模型，通过知识的应用与模型的解答来分析与解决问题，形成了“命题数学情境——提炼数学知识——探寻问题解决——考查核心素养”的试题模式.