Σ型冷弯耐候钢构件屈曲失效模式量化识别仿真研究
2023-03-25张华伟张守辉宋盼龙靳晓都宰小芬尹亚林
张华伟 张守辉 宋盼龙 靳晓都 宰小芬 尹亚林
(1.云南交通运输职业学院,云南 昆明 650300;2.河南机电职业学院,河南 郑州 451192;3.河南新亚钢构工程有限公司,河南 郑州 452470;4.河南向量智能科技研究院有限公司,河南 郑州 450000)
0 引言
冷弯成型钢构件因其加工制造高效、环保、易于实现信息化管理等优点,被广泛应用于装配式建筑等领域[1]。随着新材料、新设计方法被不断地开发出来,新材料结合截面复杂的型钢产品也越来越多。在冶炼过程中向耐大气腐蚀钢(耐候钢)中添加合金元素,使其锈层与基体之间形成一层致密的氧化物膜。此举能提高材料的耐大气腐蚀能力的同时,降低其后期维护成本,减少环境污染,从而被广泛应用于铁道车辆、桥梁、集装箱、大型厂房、建筑、输电铁塔等领域[2-7]。
影响冷弯型钢构件承载力屈曲失稳的主要形式有局部屈曲、畸变屈曲和整体屈曲。随着材料性能的提升和截面形状的复杂化,在一定条件下,畸变屈曲会控制构件的承载力[8],畸变屈曲是薄壁型钢研究和应用的新内容。在《冷弯薄壁型钢结构技术规范》(GB 50018—2002)[9]中采用传统的有效截面理论来计算稳定性能,没有充分考虑畸变屈曲的影响。目前,在《冷弯型钢结构技术规范》(征求意见稿)中,部分加劲板件的受压稳定系数的计算增加了直接强度法,也考虑了畸变屈曲的影响。弹性屈曲应力是计算和判断失效模式的重要前提,规范中普遍采用近似解析法,但该方法计算繁琐。如何定量分析屈曲失效模式是新材料和新构件在新领域中应用的前提。目前,基于广义梁理论和有限条法(FSM)开发的开源CUFSM软件在行业内得到较为广泛的应用,并能建立带约束的有限条法(C-FSM)[10-11]。
近年来,随着装配式钢结构建筑的迅速发展,冷弯成型的工艺也在不断提升,大批复杂的新型截面不断涌现。然而,耐候钢构件产品在装配式钢结构建筑领域中的应用研究还非常欠缺。本研究采用约束有限条法对不同约束和长度的Σ型冷弯耐候钢构件的轴压稳定性进行分析,为推动冷弯耐候钢材在装配式建筑领域中的应用提供参考。
1 约束有限条计算分析
1.1 约束有限条法的计算方法
有限条方法是有限元方法中的一个特例,有限条法是将薄壁截面离散成纵向条状单元,其求解过程与有限元方法类似,先得到单元刚度矩阵,然后通过集成单元刚度矩阵来求解特征值问题。传统的有限条法分析是通过对屈曲荷载和屈曲半波长的关系曲线进行观察,找到波谷点对应的屈曲模式和屈曲应力,但无法得到指定长度的屈曲模式和屈曲应力,且在波谷点不明显时,难以得到准确的结果。
Li等[11]结合广义梁理论和有限条法进行开发,并不断完善约束有线条法,解决边界条件单一等问题,可用于多种加载方式下不同屈曲模式的特征曲线分析,也可提供两种模态的有限条解的分解与模态识别[10]。约束有限条方法在求解时,先通过单元分析得到单元刚度矩阵,然后在整体分析时集成单元刚度矩阵,并求解特征值问题。在有限条方法中,刚度矩阵由弹性刚度矩阵和几何刚度矩阵构成,弹性刚度矩阵由板条单元平面内的应力刚度矩阵和平面外的刚度矩阵组成。有限条法是通过选择不同的纵向形状函数来描述不同的边界条件,从而扩展有限条法的应用范围。
Li 等[11]研究的约束有线条法可适用的边界条件包括两端铰支(simple-simple,S-S)、两端固支(clamped-clamped,C-C)、固支-铰支(simple-clamped,C-S)、固支-自由(clamped-free,C-F)、固支-滑动(clamped-guided,C-G)约束情况。有限条单元形状函数在横向方向与经典的梁的有限元相同,但在纵向方向引入了Y[m]三角函数作为形状函数,不同边界条件下的纵向形状函数如下。
两端铰支(S-S)的纵向形状函数见式(1)。
两端固支(C-C)的纵向形状函数见式(2)。
固支-铰支(C-S)的纵向形状函数见式(3)。
固支-自由(C-F)的纵向形状函数见式(4)。
固支-滑动(C-G)的纵向形状函数见式(5)。
式中:a为有限条的长度;Y[m]为纵向形状函数;m为不同边界条件下的正弦半波数。
结合纵向形状函数,构建有限条单元纵向(v)、横向(u)和厚度方向(w)的形状函数,见式(6)到(8)。
建立单元刚度矩阵,其中a、b分别为有限条的长度和宽度,μm=mπ,其他参数详见参考文献[11]。
通过约束有限条法可建立一系列用于描述屈曲类别的约束方程,将传统有限条法提供的解约束到选定的屈曲类别中,并基于不同屈曲模态的力学准则,在FSM的前提下求解纯模态时的屈曲临界应力,从而准确量化识别屈曲模式,可采用直接强度法进行计算。模态力学判断准则详见表1。

表1 模态力学判断准则
Vlasov 假设是指假设板中面的剪应力、板件横向应变为零,只产生垂直于截面的翘曲,同时横截面的形状保持不变。纵向翘曲假设是指板件的横向应变不为零,未扭曲翘曲假设则是指横向截面无扭曲发生。
1.2 受压构件弹性屈曲计算分析
本研究采用CUFSM v5.01软件分别对复杂截面耐候钢材料的受压构件在不同约束条件下的弹性屈曲进行计算分析。根据我国国家标准《耐候结构钢》(GB/T 4171—2008),耐候钢钢材通过冷轧工艺生产的高耐候钢为Q265GNH、Q310GNH。耐候钢的力学性能基本上与优质碳素钢或优质低合金钢接近[12],材料属性接近于合金钢,计算时取弹性模量为206 000 MPa、切变模量为79 380 MPa、泊松比为0.3。
结合实际的工程需求,本研究使用截面形状较为复杂的翼缘加劲卷边,建立其不同厚度(t=2 mm、2.5 mm、3 mm)时的分析模型。截面尺寸如图1 所示,截面参数见表2。计算构件模型长度分别定为1 000 mm、1 500 mm、2 000 mm、2 500 mm、3 000 mm,并结合5 种约束条件,共构建75 个计算模型,模型的变量设置见表3。
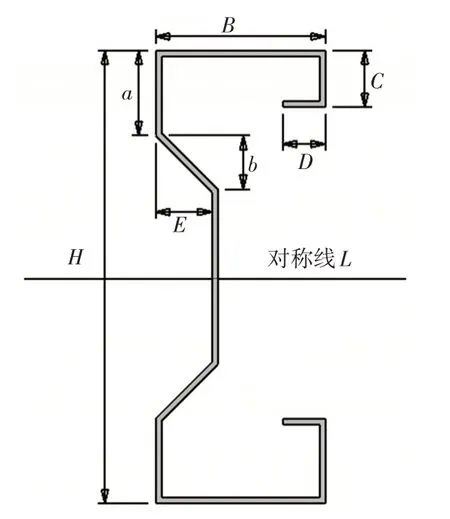
图1 截面尺寸参数示意

表2 截面参数

表3 模型变量表
为了方便计算,基于模型的变量表,对所有的分析模型按照约束条件、厚度和长度的顺序进行编号,将约束条件和厚度一致而长度不同的模型编为一组,编号结果见表4。

表4 模型编组
2 结果与讨论
2.1 模式识别
在CUFSM中选择cFSM计算纯模态下不同屈曲半波长和相应的应力。以S-S 约束下Msst3 模型为例,在该约束条件下,cFSM可识别的局部屈曲半波长为47.3 mm,相应的应力为2 558.41 MPa,畸变屈曲半波长为875.7 mm,应力为836.86 MPa,如图2所示。

图2 cFSM纯模态识别半波长和应力
以此为例,分别计算不同约束条件下的各个试件的屈曲半波长,从而定量识别不同试件屈曲计算的结果。相较于由图像来判定的屈曲模式,量化分析屈曲模式更为可靠。以M51模型(S-S约束,1 000 mm)的屈曲模式前20 阶模态定量识别结果为例,识别结果见表5。其中,整体屈曲用G来表示,畸变屈曲用D来表示,局部屈曲用L来表示,其他屈曲用O来表示。可以看出,畸变屈曲发生在第二模态,对应的临界应力fod为940.67 MPa,整体屈曲发生在第四模态,对应的临界应力为1 255.36 MPa,局部屈曲发生在第16 模态,对应的临界应力为2 384.21 MPa。由计算数据可知,试件最先发生的屈曲为畸变屈曲。
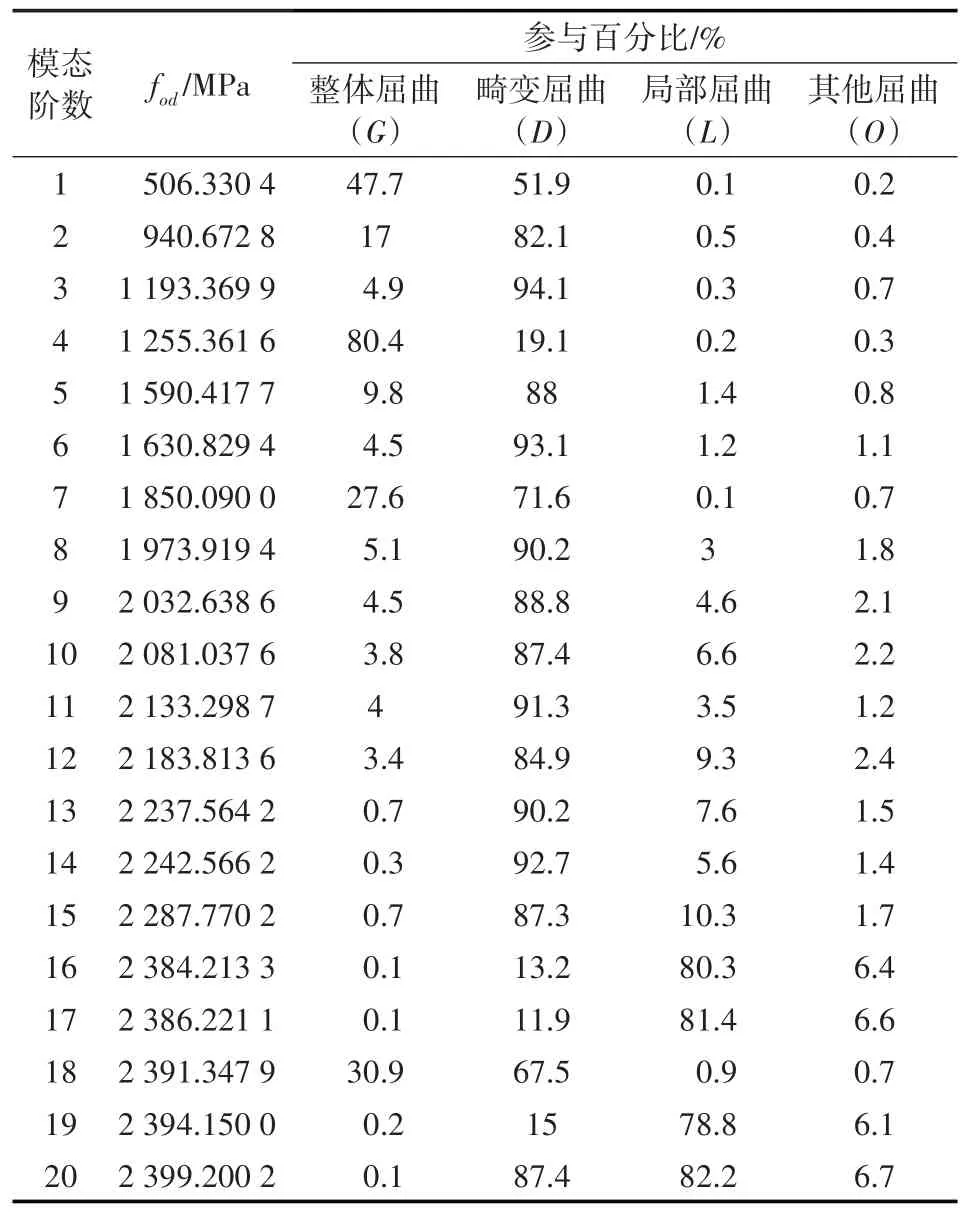
表5 S-S约束下长1 000 mm试件屈曲模式识别(序号M51)
2.2 不同约束条件对截面最小荷载的影响
在对带约束条件的有限条方法进行研究时,对不同约束和长度的试件进行分析。依据工程经验,本研究选择长度为1 000 mm、1 500 mm、2 000 mm、2 500 mm、3 000 mm的试件进行分析。1阶模态下,不同约束对Σ 截面最小荷载值的影响如图3、图4、图5 所示。其中,横坐标为构件的长度,纵坐标的荷载为1 阶模态下不同长度的构件最小屈曲应力,CUFSM 提供的计算平台可方便地计算出不同长度的屈曲应力。

图3 不同约束对Σ截面荷载值的影响(1阶模态,M1-M25,t=2 mm)

图4 不同约束对Σ截面荷载值的影响(1阶模态,M26-M50,t=2.5 mm)

图5 不同约束对Σ截面荷载值的影响(1阶模态,M51-M75,t=3 mm)
对图3 到图5 进行分析后可以发现,约束对屈曲应力的影响从大到小为C-C、S-C、C-G、S-S、C-F,构件厚度对约束和屈曲应力的关系没有显著影响,构件长度在500 mm 后对约束和屈曲应力的关系也没有显著影响。在500 mm 之前,C-F 约束的屈曲应力更低,其他约束条件下的屈曲应力比较接近。总体上,随着试件长度的增加,屈曲应力逐渐下降。其中,C-G 约束和S-S 约束对荷载的影响会随长度的增加而趋于一致。
参照上述方法,本研究对各个模型的失效模式进行分析,不同约束条件下不同长度的试件失效模式见表6(以M51-M75为例)。
从表6 可以发现,随着试件长度的增加,整体屈曲占主导地位,在S-S、C-C、C-S 约束条件下,多出现较短试件的畸变屈曲,而在C-F和C-G 约束条件下,以整体屈曲为主。

表6 M51-M75不同约束条件下不同长度屈曲模式判定 单位:mm
2.3 冷弯工艺Σ型钢构件与加载测试试验
基于上述对Σ 型钢构件失效形式的理论分析,采用冷弯成型工艺来加工成型Σ 型钢构件,并对其承载能力进行试验测试,如图6 所示。测试结果表明,冷弯成型的Σ 型耐候钢构件比Σ 型普通钢构件具有更大的承载能力,Σ 型冷弯耐候钢构件具有更好的承载能力和抗失稳能力,如图7所示。

图6 冷弯工艺生产的Σ型钢构件

图7 冷弯工艺Σ型钢构件加载测试实验结果对比
3 结语
本研究利用带约束的有限条法对Σ 截面不同厚度和不同长度的薄壁冷弯耐候钢的模型(共75个)进行屈曲模式量化识别计算。研究结果表明,①约束有限条方法可量化识别Σ 截面不同厚度和长度的薄壁冷弯耐候钢失效模式,是研究冷弯件受力学的有效方法。②构件长度大于500 mm 后,对约束和屈曲应力关系的影响并不明显。总体上,随着试件长度的增加,屈曲应力逐渐下降。③随着试件长度的增加,整体屈曲占主导地位,在S-S、C-C、C-S 约束条件下,较短试件畸变屈曲出现较多,在C-F 和C-G 约束条件下,以整体屈曲为主。④约束有限条法对分析复杂截面屈曲失效和稳定性具有高效、直观等优势,本研究可为Σ 截面的冷弯耐候钢截面的设计提供借鉴。
