Parametric Evolution of Power-law Energy Spectra of Energetic Electrons in the Coronal Loops
2023-03-25JianFeiTangDeJinWuLingChenandLeiXu
Jian-Fei Tang ,De-Jin Wu ,Ling Chen ,and Lei Xu
1 College of Engineering and Design,Lishui University,Lishui 323000,China;tjf1027@163.com
2 Key Laboratory of Planetary Sciences,Purple Mountain Observatory,CAS,Nanjing 210023,China
3 School of Physics and Electronic Information,Shangrao Normal University,Shangrao 334001,China
Abstract Fast electron beams(FEBs)are one of the main products of various active events and are ubiquitous in solar,space and cosmic plasmas.They reveal themselves in hard X-ray and radio emissions.The observed characteristics of X-ray and radio emissions sensitively depend on the energy distribution of FEBs,which usually have a power-law energy spectrum.As FEBs travel in the solar atmosphere,their energy distribution can considerably vary due to the interaction with ambient plasmas.Tang et al.investigated the evolution of the energy spectrum of the FEBs traveling along a flare loop and discussed the possible effects on associated hard X-ray(HXR)and radio emissions.Considering the ubiquitous coronal loops in active regions,in the present paper,we investigate the parametric evolution of the energy spectra of FEBs when propagating along coronal loops.Here,we take the sunpot atmospheric model as an approximate coronal loop atmosphere model.The results show that the energy loss has an important impact on the cutoff behavior and energy spectra of FEBs when precipitating in a coronal loop with density ratio nb/ne=0.01.The initially single power-law spectrum with a steepness cutoff can evolve into a more complex double power-law spectrum or two “knees” power-law spectrum with a flattened steepness cutoff behavior or saturation cutoff behavior.Our calculations also demonstrate that the energy spectrum evolution is not obvious if nb/n0=0.001 as Tang et al.asserted.The present results are helpful for a more comprehensive understanding of the dynamic spectra of HXR and radio emissions from FEBs.
Key words: Sun: activity–Sun: flares–Sun: radio radiation
1.Introduction
Based on its high resolution and large field of view,the Transition Region and Coronal Explorer (TRACE) has obtained some excellent extreme ultraviolet (EUV) images and movies.These observations have changed our understanding of the corona,especially of active regions,which appear to be made entirely by loop structures (Del Zanna &Mason 2003).Although coronal loops have been well defined and studied in the EUV band,we should still be aware that most coronal loops are also visible in X-ray band.So when observed with X-ray spectroscopy,the whole X-ray bright corona also consists of magnetic loops.Coronal loops are magnetic structures with an approximate semicircular shape,which are filled with hot and dense plasma.They generally originate in strong unipolar regions and end up in either different active regions or connect two polarities across a neutral line (Schrijver et al.1999).According to the length of coronal loops,they can be divided into bright points (∼108cm),active region loops(109–1010cm)and giant arches(∼1011cm) (Reale 2010).The fully ionized plasma is confined in the coronal loops and isolated from the ambient plasma.Such magnetized plasma is well insulated because it conducts most of the thermal energy along the magnetic field.Thus,coronal loops have different temperatures and can be roughly divided into cold loops (∼105K),X-ray loops (to a few 106K) and flaring loops (up to a few 107K) (Reale 2010).The typical values of the plasma density of coronal loops are 109–1010cm−3,while flare loops have densities of at least one order of magnitude denser (Reale 2010).In this paper,“coronal loops” are defined as X-ray loops with typical density of 109–1010cm−3and temperature of a few 106K,excluding flare loops.
Accelerated electrons are ubiquitous in space and cosmic plasmas (Narukage et al.2014).For the Sun,there are several mechanisms for electron acceleration: magnetic reconnection,coronal shock waves,and even the interaction between coronal mass ejection and the background magnetized plasma loops(Tan et al.2019).During a flare,enormous magnetic energy is suddenly released and transferred partly into the thermal and kinetic energies of energetic particles such as electrons,protons and heavy ions (Masuda et al.1994;Yokoyama et al.2001;Hara et al.2011;Imada et al.2013).These flare accelerated electrons travel along solar magnetic fields and form fast electron beams(FEBs).They can be inferred from their excited radio bursts and hard X-ray(HXR)bursts when they propagate in the solar atmosphere (Lin &Schwartz 1987;Dulk et al.1992;Holman et al.2011),and even can be detected directly by particle detectors when FEBs travel into near-Earth interplanetary space (Lin 2011).It is believed that FEBs propagate downward along the magnetic field,and the small pitch angles precipitating electrons will hit the denser chromosphere and excite HXR emissions via bremsstrahlung(Aschwanden et al.1995).So,X-ray radiation is a more direct window which provides important information on acceleration and transportation processes of the FEBs.Flare HXR observations show that there are usually a corona source and two footpoint sources in the chromosphere.The standard HXR emission model involves the thin-target bremsstrahlung in the corona source and the thick-target bremsstrahlung in the footpoint sources.In this standard model,power-law FEBsF0(E)∝E−δwill emit HXR with spectravia the thin-target bremsstrahlung in the corona source,here γtp=δ+1 is the photon spectral index (Holt &Cline 1968;Syrovatskii&Shmeleva 1972;Lin&Hudson 1976;Hannah&Kontar 2011).If the FEBs do not lose energy,they will produce HXR spectravia the thick-target bremsstrahlung in the chromosphere,here γft=δ −1(Brown 1971;Hannah &Kontar 2011).So,the acceleration and transport processes of FEBs can be well constrained if the HXR emissions from the corona source to the footpoint sources are both observable.
According to this simple scenario that the same FEBs produce the coronal source via thin-target bremsstrahlung and the footpoint sources via thick-target bremsstrahlung,the difference between the two photon spectral indices should be Δγ=γtp−γft=2 (Hannah &Kontar 2011;Holman et al.2011;Simes &Kontar 2013).However,observations demonstrate that most flare events with the predicted spectral index difference are inconsistent with the standard model.Masuda et al.(2000) found a difference in spectral indices of the coronal and footpoint sources which were observed simultaneously for the first time by Masuda et al.(1994) with Δγ<2.Petrosian et al.(2002)made a comprehensive analysis of 18 Yohkoh events and found that the spectral index of the coronal source is softer than that of footpoints on average by about 1.Battaglia &Benz (2006) analyzed five flares by examining the relation between coronal and footpoint sources and found that the average of all mean differences is about 1.8,and the differences of two events is larger than 2 and that of the other three events is smaller than 2.This inconsistency excludes the simple scenario that FEBs are freely propagating from the acceleration site to the footpoints and indicates that other transport effects must be considered.
On the other hand,the X-ray images with spectral capabilities enabled by Reuven Ramaty High Energy Solar Spectroscopic Imager (RHESSI) carry a wealth of information about the energetic electrons.One of the most important findings by RHESSI is that many flares present a double power-law spectrum (Kontar et al.2002;Conway et al.2003;Holman et al.2003).Furthermore,the spectral index of the double power-law photon spectrum at lower energy is usually smaller than that at higher energy.Various possible physical processes have been proposed to interpret the double powerlaw spectrum of HXR,such as (1) the inhomogeneous ionization along the path of FEBs (Brown 1973;Kontar et al.2003;Su et al.2011),(2) the instabilities of plasma(Holman et al.1982;Melrose 1990;Hannah &Kontar 2011),(3)the photospheric albedo caused by Compton backscattering(Bai &Ramaty 1978;Jeffrey &Kontar 2011),(4) the acceleration process of energetic electrons (Lin &Hudson 1971) and (5) the energy losses (Holman et al.1982;Alaoui &Holman 2017).The electron acceleration process or energy loss indicates that the energetic electrons have an initial broken power-law spectrum as they leave the acceleration site or they will evolve into such a double power-law distribution during propagation,respectively.
When FEBs travel in the solar atmosphere,they will lose part of their energy due to various energy loss mechanisms.In general,there are two main types of energy loss processes,the collisional energy loss due to Coulomb collisions with ambient plasma(Masuda et al.2000;Petrosian et al.2002;Zharkova&Gordovskyy 2006),and the noncollisional energy loss due to deceleration by induced electric fields.As presented by van den Oord (1990),an induced current (i.e.,a return current) will be driven rapidly by the induced electric field and neutralize their carried ultrastrong beam current when FEBs travel along the magnetic field in the solar atmosphere.The energy of FEBs will inevitably be extracted by the induced electric field,which decelerates the FEBs.Numerous works have discussed the influence of induced current on FEBs and the ambient plasma(Emslie 1980,1981;Zharkova &Gordovskyy 2006;Battaglia&Benz 2008;Holman 2012;Xu et al.2013;Alaoui &Holman 2017).Considering the effects of return currents and collisions,Emslie (1980),Emslie (1981) studied the energy loss and heating rate of the power-law FEBs with a saturation low-energy cutoff behavior.Based on the analytic solution of the return current loss and an initial power-law FEB with a sharp cutoff behavior,Holman(2012)investigated the effect of the return current on the X-ray emission.Alaoui &Holman(2017)explained the breaks of the HXR spectrum around a few deka-keV with the return current model.They also adopted an initial power-law energy spectrum with a sharp cutoff behavior.
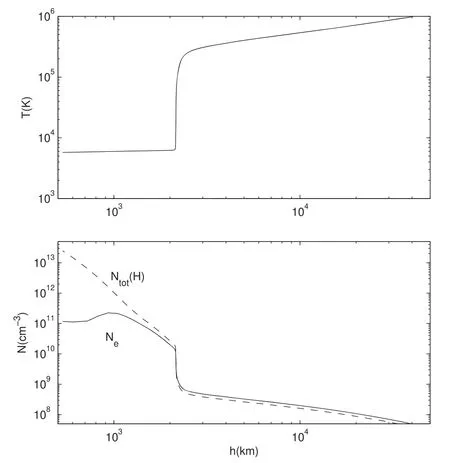
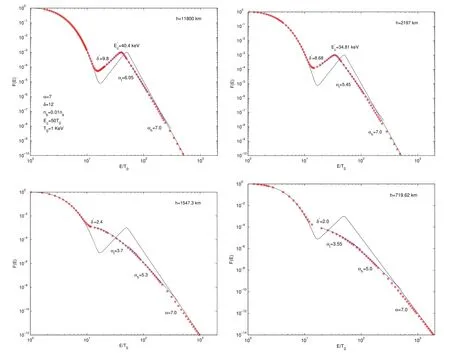
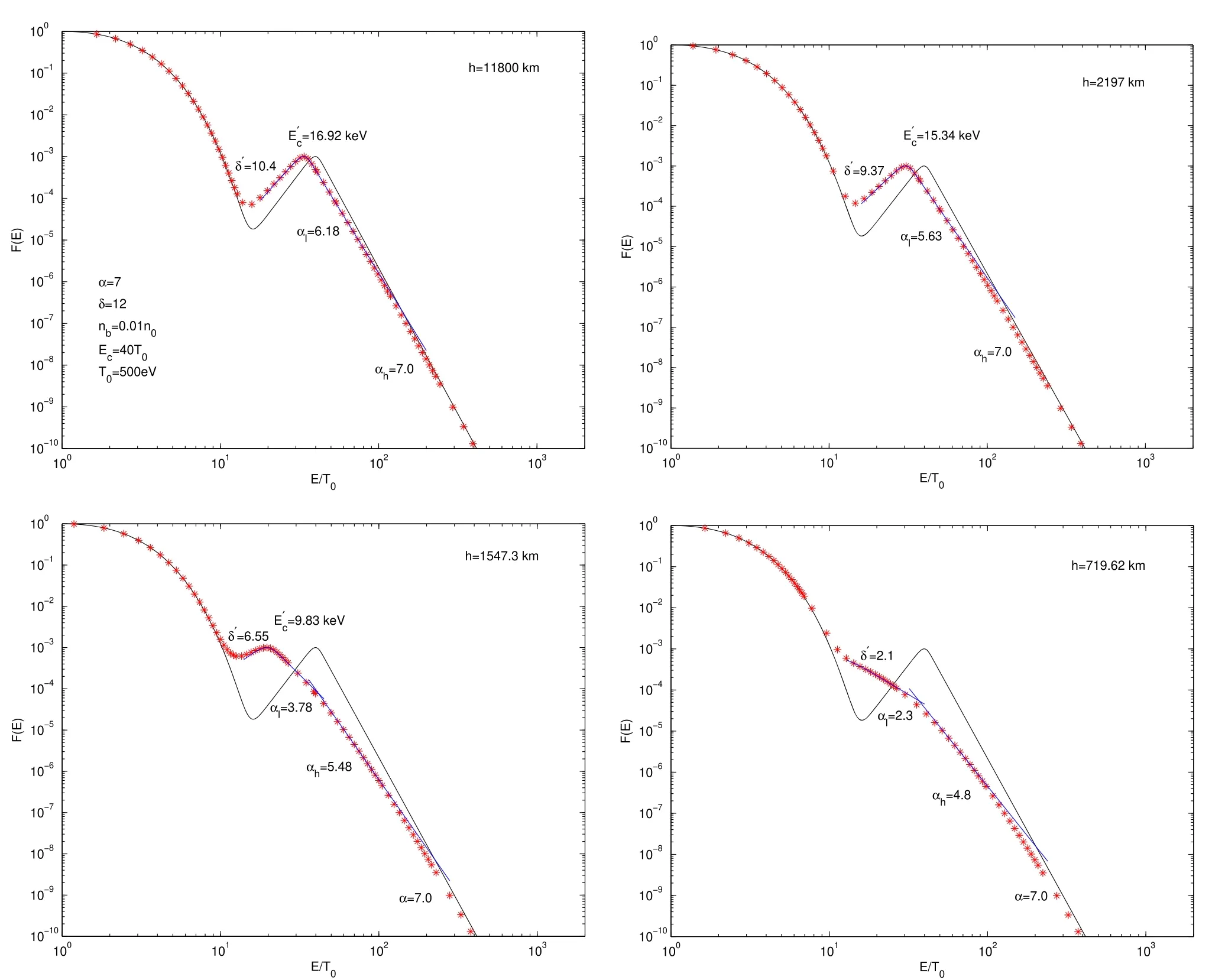
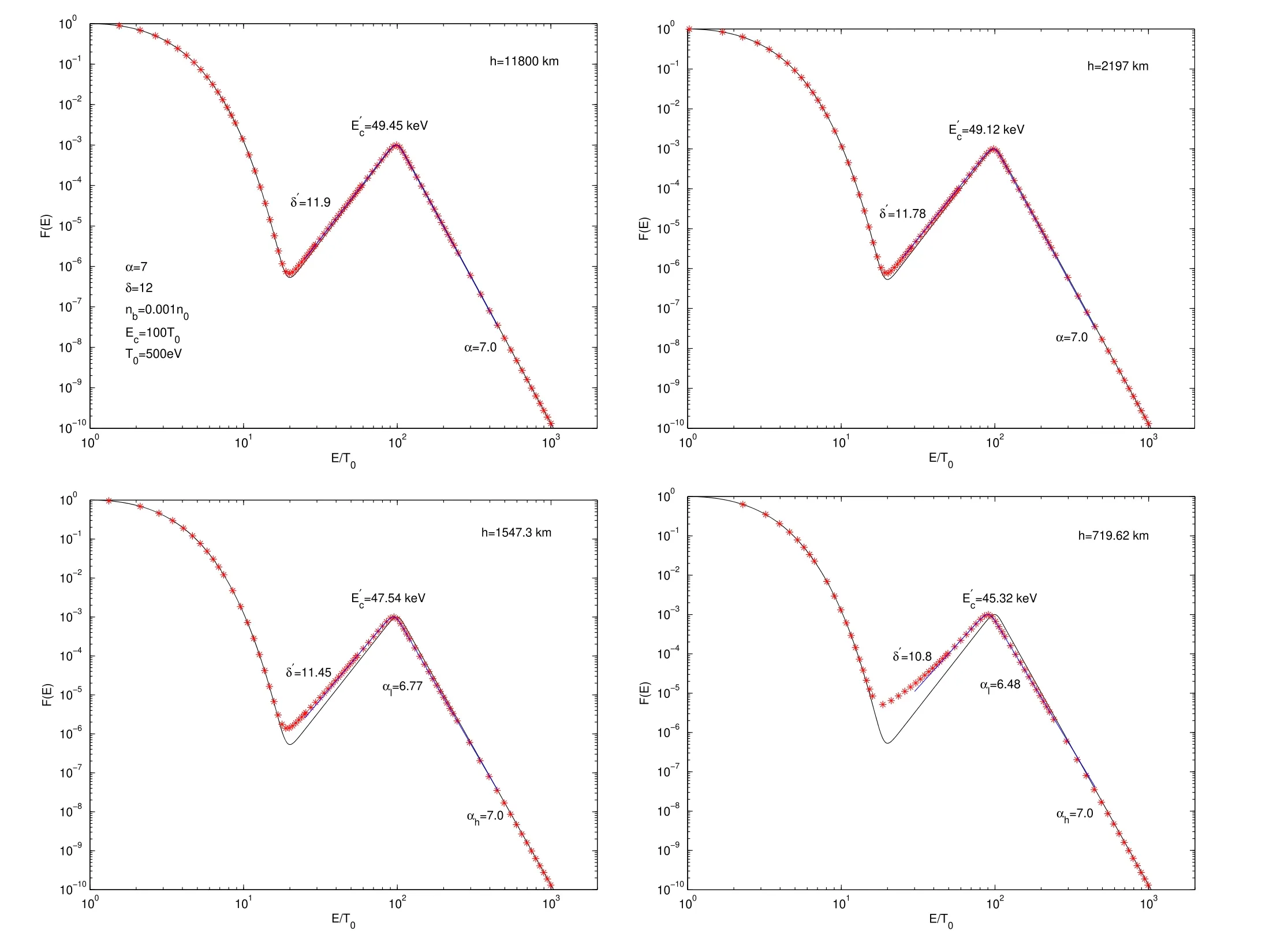
Observations demonstrate that the energy distribution of FEBs usually exhibits a power-law spectrum approximately,with a lower energy cutoff around deka-keV(Lin 1974;Bastian et al.1998;Aschwanden 2002).It is difficult to identify the cutoff energy and the specific form of the cutoff behavior from observations.Therefore,as mentioned above,researchers often adopted extreme assumptions.One is the sharp cutoff behavior,that isF(E)=0 for energiesE HereEdenotes the energy of the energetic electrons,andAbis the normalization factor.The lower-energy cutoff behavior of the power-law spectrum of the FEBs is described by a hyperbolic tangent function tanh,and δ andEcare the steepness index and cutoff energy,respectively.α is the spectral index of the power-law spectrum.Wu &Tang (2008)showed that the lower-energy cutoff behavior will approach the sharp cutoff case if δ ≫α and the saturation case if δ ≤α. In a recent work,Tang et al.(2020)analyzed the parametric evolution of the power-law spectrum of FEBs traveling through a flare loop and discussed the possible effects on the associated HXRs and solar radio bursts (SRBs).They adopted the initial energy spectrum of FEBs as Equation(1).As mentioned above,active regions are characterized by ubiquitous loop structures.In addition to the flare loops,there are many coronal loops,which have a lower density and temperature than that of flare loops but higher than that of the ambient plasma.Due to the complex magnetic field structure of active regions,there are various burst events,such as emergence of magnetic flux,flares,filament eruptions and so on.Some of the accelerated electrons from these events travel in the flare loops,while the remaining accelerated electrons inevitably will propagate along the coronal loops.Although most coronal loops may not be rooted in the umbrae of sunspots,there are still many works that investigate whether coronal loops connect into sunspot umbrae.Foukal (1975) pointed out that the brightest coronal loops observed in the EUV band are associated with the flux tubes leading to sunspot umbrae.Several short-lived (<300 s),subarcsec bright dots have been observed above sunspots in addition to penumbrae in the transition region by Tian et al.(2014).According to Atmospheric Imaging Assembly (AIA)observations,they suggested that these bright dots are located at the base of loop structures.Straus et al.(2015) reported a burst of supersonic downflows above the lightbridge in a sunspot and interpreted their results as evidence of the termination shock in a cool umbral loop.Dammasch et al.(2008) indicated that the sunspot plumes are the common footpoints of several coronal loops.Because of the weak emission in the umbra,Chitta et al.(2016) reported on the umbral loops and traced them to their other footpoints,which were also rooted close to the umbra of the opposite polarity sunspot.In this paper,based on the semiempirical sunpot atmospheric model (Avrett et al.2015),we investigate the parametric evolution of the FEBs during their propagation along coronal loops due to the energy losses.The rest of the paper is organized as follows.Section 2 introduces the sunpot atmospheric model and energy loss mechanisms.The energy loss and evolution of the energy spectrum of FEBs are presented in Section 3.Finally,a brief summary is given in Section 4. It is generally thought that HXR emission is attributed to bremsstrahlung.Flare-accelerated electrons propagate downwards along magnetic field lines into the denser chromosphere,then stop and heat the ambient plasma via Coulomb collisions(Brown 1971;Brown et al.2003).These accelerated electrons of FEBs will lose their energy via interaction with the background dense plasma while they propagate in the coronal loops.There are two main types of energy loss mechanisms,i.e.,collisional energy loss and noncollisional energy loss.Collisional energy loss is caused by Coulomb collisions with charged particles and neutral particles,and the noncollisional energy loss is due to deceleration by the induced electric field.The energy loss of the energetic electrons in FEBs is where the subscripts coll and rc indicate the energy loss by collision and deceleration of induced electric field,respectively.For hydrogen and helium solar plasma,neglecting the energy loss by protons and helium ions,and assuming that the speeds of FEBs are much greater than the mean speed of the background electrons,the collisional energy loss rate can be written as (Brown 1971;Emslie 1978;Holman et al.2011) Here,eis the electronic charge,whileEandvdenote the energy and velocity of energetic electrons of FEBs,respectively.neandnzare the number density of electrons and that of an element with atomic numberZin the ambient plasma,respectively.χzis the ionization rate of an element with atomic numberZ.is the Coulomb logarithm for electron-electron collisions,andis the effective Coulomb logarithm for the interaction of a energetic electron with an atom.λDis the Debye length,andIzis the ionization potential of a hydrogen or helium atom. For the noncollisional energy loss rate,i.e.,the energy loss via deceleration in the induced electric field,can be written as(Holman 2012) Here,Eiis the induced electric field driven by FEBs.In the steady state,according to Ohm’s law,Eican be derived as(Tang et al.2020) Herenbandvbare the density and beam speed of FEBs,respectively.Parameter β is the excited level of ion-acoustic turbulence.meis the mass of an electron,andTeis the temperature of background plasma in the unit of eV. Noting thatvdt=−dh,from Equations (3) and (4) we can obtain the total energy loss ΔEjof beam electrons in thej-th layer from integral HereEj−1andEjare the energies of beam electrons at the top and bottom of thej-th layer,respectively.lj=hj−1−hjis the thickness of thej-th layer.If the density,temperature of background plasma and the induced electric field are approximated as constants in a single layer,the energy loss of the energetic electrons of FEBs can been obtained as Although a lot of EUV and X-ray loops in the solar corona are not rooted in the sunspot umbrae,they still connect to the enhanced magnetic active region.Therefore,we believe that the plasma environment of the coronal loops is close to the sunspot atmosphere model.In this paper,we consider a semiempirical sunspot model proposed by Avrett et al.(2015).Compared with the flare model (Tang et al.2020),the transition region of the sunspot atmosphere model is about 1000 km higher than that of the flare model.As mentioned in the Introduction,the temperature and density of the sunspot model are lower than those of the flare model,and the density is at least two orders of magnitude lower.Figure 1 plots the temperature and density distribution of the background plasma versus heighthalong the coronal loop.According to the sunspot model,we take the height of the loop top to beh=5.81×104km.From the loop top to the bottom of the chromosphere(about 500 km),the coronal loop is divided into more than 90 layers.The height,temperature and density of the background plasma of each layer can be referred to in table 2 of Avrett et al.(2015).When calculating the energy loss of the FEBs in each layer with Equations (8) and (9) we assume that the temperature,density and induced electric field are constant in each layer,and we take these constants as the average values of the upper and lower boundaries of each layer. Figure 1.The temperature and density of background plasma as a function of height h along the coronal loop. Figure 2.The evolution of the FEBs due to energy loss when traveling along the coronal loops and reaching heights h=11,800 km,2197 km,1547.3 km and 719.62 km.Here,the cutoff energy Ec=50 keV,steepness index δ=12 and spectral index α=7 of the initial FEBs.Ambient plasma temperature T0=500 eV. As FEBs propagate downward along the coronal loops,the energetic electrons of FEBs will lose some of their energy due to Coulomb collisions and deceleration from the induced electric field.Based on the sunspot atmosphere model and Equations (8) and (9) we can calculate the energy lossand the remaining energyEjof the energetic electrons of FEBs when they arrive at a certain heighthjfrom the loop top.As mentioned above,observations from HXR and radio radiation demonstrate that the energy distribution of energetic electrons usually can be approximated by a negative power-law spectrum (Lin 1974;Aschwanden 2002),so the initial single power-law FEBswill evolve into a complex spectrumF(E)∝(E+ΔE)−δdue to the energy loss ΔE.In the same way as Tang et al.(2020),we take the initial energy distribution function of FEBs as and at the looptop,it will evolve into the final form because of the energy loss ΔE Here,like in Equation (1),Abis the normalization factor,the hyperbolic tangent function tanh (E0/Ec)δdescribes the lowerenergy cutoff behavior andEcis the cutoff energy.Since we only consider the energy change of the energetic electrons during their travel,the number of electrons with energyE=E0−ΔEin Equation (11) is equal to the number of electrons with energyE0in Equation(10).That said,the energy distribution in Equation(11)is derived directly from the initial distribution Equation (10) in terms of the energy loss ΔE. Figures 2–5 show the parametric evolution characteristics of the energy spectrum of FEBs propagating in the coronal loops.The four panels plot FEBs arriving at heightsh=11,800 km,2197 km,1547.3 km,and 719.62 km,respectively.The initial number density of energetic electrons of FEBsnb=0.01nein Figures 2–4,andnb=0.001nein Figure 5 have been used.The exciting level of ion-acoustic turbulence is assumed to β=10 in the coronal and transition region,and β=0 in the chromosphere.Here,the initial energy distribution of the FEBs is displayed as solid lines,which are superimposed on the thermal distribution of background plasma.The red stars signify the ultimate energy distribution of FEBs when they arrive at a certain height.The blue lines are the fitting results with Equation (10) and power-law distribution. Figure 3.The evolution of the FEBs due to energy loss when traveling along the coronal loops reaches heights h=11,800 km,2197 km,1547.3 km and 719.62 km.Here,the cutoff energy Ec=50 keV,steepness index δ=12 and spectral index α=7 of the initial FEBs.Ambient plasma temperature T0=1 keV. In Figure 2,the initial power-law FEBs have the cutoff energyEc=50 keV,steepness index δ=12 and spectral index α=7.The temperature of background plasmaT0=500 eV has been used.The beam electrons lose some of their energy via Coulomb collisions and decelerate by the induced electric field when traveling along the coronal loops;the deeper the FEBs are precipitated,the more the electrons lose energy.Some of the energetic electrons will be thermalized and become the background electrons when they lose most of their energy.The lower energy cutoff behavior and the spectral characteristics of the FEBs will change significantly due to the energy loss ΔEbeing related toE0.Figure 2 shows that the initial single powerlaw spectrum of FEBs will turn into a double power-law spectrum or two knees power-law spectrum.The steepness cutoff behavior of FEBs will move toward lower energy and flatten out.From Figure 2,one can find that the cutoff energyand the steepness indexδ′ are about=44.95 keV,δ′=10.78 at heighth=11,800 km,=42.16 keV,δ′=9.7 ath=2197 km,=31.71 keV,δ′=7.6 ath=1547.3 km,and=23.74 keV,δ′=5.7 ath=719.62 km,respectively.For the double power-law spectrum atE>in the top two panels,we take the initial spectral index as the spectral indices of the higher energy part,i.e.,αh=7.0,and fit the spectral indices of the lower energy part αlas αl=6.44 and αl=5.71.For the two knees power-law spectrum in the bottom two panels,we have the spectral indices αl=4.6,αh=5.7,α=7.0 at height 1547.3 km,and αl=3.6,αh=5.0,α=7.0 at 719.62 km,respectively. Figure 4.The evolution of the FEBs due to energy loss when traveling along the coronal loops reaches heights h=11,800 km,2197 km,1547.3 km and 719.62 km.Here,the cutoff energy Ec=20 keV,steepness index δ=12 and spectral index α=7 of the initial FEBs.Ambient plasma temperature T0=500 eV. In Figure 3,the temperature of ambient plasmaT0=1 keV,and parameters of the initial FEBs,such as the cutoff energyEc,steepness index δ and spectral index α are the same as in Figure 2.Figure 3 also confirms that the energy spectrum and cutoff behavior of the initial FEBs have changed.The energy spectrum can be fitted with a double power-law spectrum ath=11,800 and 2197 km,and a two knees power-law spectrum ath=1547.3 km and 719.62 km.As the FEBs travel downward,the cutoff energyEcalso decreases and the steepness cutoff behavior finally turns into the saturation cutoff behavior.From Figure 3,one can find that the top two panels have the cutoff energies and steepness index,respectively.The spectral indices of the double power-law are αl=6.05,αh=7.0 ath=11,800 km,and αl=5.54,αh=7.0 ath=2197 km,respectively,and the break energy is between 100 ∼200 keV.For the two knees power-law spectrum in the bottom panels of Figure 3,the spectral indices are αl=3.7,αh=5.3,α=7.0,and αl=3.55,αh=5.0,α=7.0,respectively.The two breaks are between 70 ∼80 keV and 300 ∼400 keV,respectively. Figure 5.The evolution of the FEBs due to energy loss when traveling along the coronal loops reaches heights h=11,800 km,2197 km,1547.3 km and 719.62 km.Here,the number density of the energetic electrons of FEBs nb=0.001ne,and other parameters of the initial FEBS and ambient plasma are the same as in 2. In Figure 4,the initial cutoff energyEc=20 keV has been used,but other parameters of initial FEBs and temperature of ambient plasma are the same as in Figure 2.From Figure 4,one can find that the steepness cutoff behavior becomes flat and the cutoff energy also decreases.It finally evolves into the saturation cutoff behavior in the last panel.The cutoff energy and steepness index are about,respectively.The top two panels in Figure 4 also affirm that the energy spectra can be well fitted with the double power-law spectrum.The spectral indices are αl=6.18,αh=7.0 and αl=5.63,αh=7.0 at heightsh=11,800 km and 2197 km,respectively,and the break energy is between 50 and 100 keV.For the two knees power-law spectrum ath=1547.3 km and 719.62 km in the two bottom panels,the spectral indices are αl=3.78,αh=5.48,α=7.0,and αl=2.3,αh=4.8,α=7.0,respectively. In Figure 5,the density of the energetic electrons of FEBs is taken to benb=0.001ne.Other parameters of the initial FEBs areEc=50 keV,δ=12 and α=7,and the temperature of the background plasma isT0=500 eV.Due to the low density of the beam electrons,Figure 5 shows that the evolution of the energy spectrum of the FEBs is not significant.When the FEBs travel downward from the looptop to the chromosphere footpoint along coronal loops,the low-energy cutoff behavior and the cutoff energyEcare only slightly flattened and decrease.The cutoff energies are about=49.45 keV,49.12 keV,47.54 keV and 45.32 keV,and the steepness indices areδ′=11.9,11.78,11.45 and 10.8 ath=11,800 km,2197 km,1547.3 km and 719.62 km,respectively.One also can find from Figure 5 that the power-law energy spectrum of FEBs does not change significantly.The upper two panels still have a single power-law distribution,while the bottom two panels can be fitted with the double power-law spectrum.For the double power-law distribution ath=1547.3 km and 719.62 km,the spectral indices are αl=6.77,αh=7.0,and αl=6.48,αh=7.0,respectively,and the difference between the two indices is inapparent. Figure 6.The evolution of the cutoff energy Ec of FEBs when traveling along the coronal loops,the parameters of the initial FEBs and ambient plasma are the same as in 2. Figure 6 plots the evolution of the cutoff energyEcof the power-law spectrum of the FEBs when they precipitate along the coronal loops.Here,the initial parameters of FEBs as cutoff energyEcand number densitynb,the excited level of ionacoustic turbulence β and the ambient plasma parameters are the same as in Figure 2.As FEBs propagate downwards along the coronal loops,Figure 6 clearly demonstrates that the cutoff energyEcdecreases slowly at first,and then decreases rapidly when the FEBs reach the transition region.This indicates the higher energy loss rate in the transition region and chromosphere than in the corona. Energetic electrons are ubiquitous in space and cosmic plasmas.For the Sun,energetic electrons are usually accelerated by the magnetic reconnection process of flares or by a corona shock wave.A typical large solar flare,for example,can release huge amounts of magnetic energy of about 1030–1033erg in a short period of time (Hudson 2011).The rapid release of magnetic energy causes a large number of particles to be accelerated to a high energy state in a short time.Accelerated electrons travel along the magnetic field lines in the solar atmosphere and emit radiation from γ −ray to radio emission.It is generally believed that when FEBs propagate in the magnetic field,they will produce radio radiation (such as type III bursts) and HXR emission.The former is usually generated by the plasma emission mechanism or cyclotron maser emission mechanism,and the latter is generated via bremsstrahlung due to the electrons with small pitch angles that precipitate into the denser chromosphere.High-resolution observations of HXR and radio emission can provide a wealth of information about the physics of acceleration and propagation of FEBs.As Holman et al.(2011) point out,the location where FEBs emit radiation is not necessarily where they are accelerated.Some puzzles remain,such as the inconsistency of the index difference between the traditional thin-thick target X-ray model with observations (Hannah &Kontar 2011;Holman et al.2011),the difficult to explain spectrum break (Alaoui &Holman 2017) and the so-called particle number problem (Brown 1972) required to extend the interpretation of X-ray emission from the purely collisional energy loss to consideration of noncollisional energy losses due to the deceleration in the induced electric field. Tang et al.(2020) studied the evolution of the energy spectrum of the FEBs and discussed the possible effects on the HXRs and radio radiation as FEBs traveling through the flare loops.Observations from X-ray and EUV show that solar active regions are almost composed of loop structures which are connected to the enhanced magnetic active region.A flare loop is one type of the coronal loop and has the highest temperature and density.As mentioned earlier,in addition to flare loops,there are many coronal loops with low temperature and density.Therefore,we believe that some of the accelerated electrons will inevitably enter and travel along the coronal loops.In this paper,we consider power-law injected FEBs as Tang et al.(2020)did and investigate their evolution due to the energy loss as propagating along the coronal loops. As Tang et al.(2020) presented,the energy loss of beam electrons will change the energy spectrum distribution of FEBs when propagating in flare loops.Our results also consider the evolution of the energy spectrum of FEBs,but it becomes much weaker in coronal loops than in flare loops.In Figure 5,the parameters of initial FEBs and ambient plasma are consistent with Figure 3 of Tang et al.(2020),but the lowenergy cutoff behavior and the cutoff energyEcof FEBs are only slightly flattened and decrease as they travel from looptop down to the chromosphere.In view of the fact that the plasma density of the coronal loop is 1–2 orders of magnitude lower than that of the flare loop,the density ratio parameternb/n0in the coronal loop should be 1–2 orders of magnitude higher,assuming that the number of energetic electrons entering the coronal loop and flare loop is comparable.So,we take the density rationb/n0=0.01 in Figure 2–4.Similar to Tang et al.(2020),our calculations demonstrate that the steepness cutoff behavior of FEBs will be flattened and even turn into the saturation cutoff behavior,and the single power-law spectrum of initial FEBs can evolve into a double power-law spectrum or a two knees power-law spectrum when precipitating at a certain height.These evolution results of the energy spectrum of FEBs will also cause the corresponding observational effects in HXR and radio emissions. As mentioned above,the FEB spectrum can be inferred from the photon spectrum of HXR based on the bremsstrahlung mechanism.The most important feature of the FEB spectrum is that it usually exhibits a double power-law spectrum(Lin &Schwartz 1987;Dulk et al.1992;Kontar et al.2002;Conway et al.2003;Holman et al.2003;Chen et al.2021).Lin&Schwartz (1987) reported a well fitted double power-law HXR spectrum in the impulsive phase of the 1980 June 27 flare,and the break knee is between 25 and 60 keV.Dulk et al.(1992)investigated 93 HXR flares and found that almost all the HXR spectra would break down into a double power-law spectrum at about 100 keV when reaching the peak emission.The difference in spectral indices between the lower and higher energy parts is about 1 −2.By combining the HXR and microwave observations,Chen et al.(2021) studied an X8.2 limb flare on 2017 September 10 and derived the energetic electron distribution of the source in the impulsive phase.They also fitted the nonthermal tail from ∼16 keV as a double power-law spectrum,which breaks down at ∼160 keV with the spectral indices ∼3.6 below and >6.0 above the break energy.Although many physical mechanisms have been proposed to interpret the double power-law spectrum of energetic electrons,the energy loss process cannot be ignored.Our calculation results show that the initial single power-law spectrum of FEBs can evolve into the double power-law or two knees power-law spectrum (Figures 2–4).The difference in spectral indices of the power-law spectrum below and above the break energy is about 1 −2,and the break energy is between tens to hundreds of keV.We believe that such a double power-law distribution of FEBs can produce the break power-law HXR spectra as Dulk et al.(1992),and Chen et al.(2021) observed. The very similar temporal behavior between HXR and SRBs indicates that they have a common nonthermal source,FEBs.Therefore,the spectral indices of the two emissions should be correlated directly.However,a lot of previous studies indicate that the spectral indices of FEBs derived from microwave and HXR observations are usually different (Kundu et al.1994;Silva et al.2000;Asai et al.2007,2013).This is attributed to the fact that microwave emission is mainly dominated by electrons above 300 keV,whereas HXR radiation is sensitive to electrons with tens of keV (White et al.2011).So,it is desirable to have HXR emission up to several hundred keV when comparing the spectral indices deduced from these two emissions.Some studies have found that the radio-deduced and HXR-deduced spectral indices are compatible at energies above several hundred keV (Trottet et al.1998;Vilmer et al.1999;da Silva &Valio 2021).This is consistent with our results qualitatively.Because of the energy loss of energetic electrons,which is dependent on the initial energy,the FEBs will evolve into a double or two knees power-law spectrum when precipitating along the coronal loops.The break energy that separates the two power-law parts is between tens and hundreds of keV(Figures 2–4).We can find from these figures that the spectral indices of the lower-energy parts are 1 −2 lower than those of high-energy parts (above several hundred keV),while the spectral indices of the high-energy parts hardly change during their propagation.This may explain why there is usually a discrepancy between spectral indices deduced from HXRs (low energy) and radio emissions,while having comparable spectral indices when HXRs are at energies above several hundred keV. The lower energy cutoff behavior of FEBs can provide free energy for electron cyclotron maser emission (ECME).Our results show that the initial steepness cutoff behavior of FEBs will flatten and even turn into a saturation cutoff behavior.One can expect the possible effects of these evolving FEBs on the radio emission excited by ECME.Tang et al.(2016) roughly studied the ECME growth rates of evolving FEBs due to energy loss and the variation of ambient plasma parameters when traveling in the solar atmosphere.They found that the evolution of FEBs has a prominent influence on the ECME and hence the burst types of SRBs.In this paper,we do not consider the influence of other factors on the evolution of the FEB spectrum.Further elaboration and systematic investigation are needed. Acknowledgments We thank the anonymous referee for valuable suggestions that improved the manuscript very much.This work is supported by the National Natural Science Foundation of China(NSFC,Grant Nos.12173076,42174195,11873018 and 41531071),by Lishui University Initial Funding under grant QD2182,and by NSF of Jiangsu Province under grant BK20191513.2.Energy Loss Mechanisms and the Sunspot Atmospheric Model
2.1.Energy Loss Mechanisms
2.2.Sunspot Atmosphere Model

3.Parametric Evolution of the Energy Spectrum of FEBs in Coronal Loops

4.Summary and Conclusion
杂志排行
Research in Astronomy and Astrophysics的其它文章
- Formation and Destiny of White Dwarf and Be Star Binaries
- Determination of Distance,Extinction,Mass,and Age for Stars in LAMOST DR7
- Fractions of Compact Object Binaries in Star Clusters: Theoretical Predictions
- A Two-limb Explanation for the Optical-to-infrared Transmission Spectrum of the Hot Jupiter HAT-P-32Ab
- The First Photometric and Spectroscopic Study of Contact Binary V2840 Cygni
- Galaxy Interactions in Filaments and Sheets: Effects of the Large-scale Structures Versus the Local Density
