借助整体思想 走出数学解题困境
2023-03-23黄火根
黄火根
(福建省上杭县第五中学,福建 龙岩 364031)
众所周知,高中数学习题情境复杂多变.要想成功、顺利地解题,不仅需要牢固地掌握基础知识,更要了解与掌握数学思想应用意识.其中整体思想在高中数学解题中有着广泛地应用,教学实践中应注重结合具体教学内容做好整体思想在解题中的应用讲解,更好地激活学习者的解题思维,提升其解题能力.
1 借助整体思想,解答函数习题
函数是高中数学的重要知识点,相关习题更是复杂多变.解答函数习题常使用函数的相关性质.对于部分函数习题需要运用整体思想,对要求解的问题进行处理.教学实践中,为使学习者能够运用整体思想走出解题困境,一方面,为学习者灌输整体思想相关理论,使其认识到什么是整体思想,运用整体思想解答函数习题的必要性,无形之中认识到整体思想的重要性;另一方面,为使学习者更好地掌握整体思想解答函数习题的相关思路以及相关应用技巧,避免在应用的过程中走弯路,课堂上应注重与学习者一起剖析典型习题,尤其鼓励学习者积极开展讨论活动,思考将哪一部分当做一个整体,以更好地应用函数相关知识,给学习者留下深刻印象的同时,迅速地找到解题的突破口.例如在完成函数奇偶性内容讲解后,课堂上与学习者一起剖析如下习题,使学习者认识到遇到较为复杂函数解析式的问题时,应通过整体思想的应用巧妙地转化,减少不必要地运算,迅速解题.

解析观察可知函数f(x)的解析式较为复杂,而且g(x)从题干给出的条件中无法求得g(x)具体的解析式,因此,不能直接运用其单调性求解最值.该题看似无从下手,但是从函数奇偶性角度分析,运用整体思想不难得出正确结果.
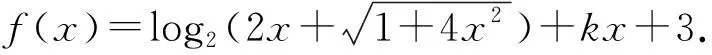
2 借助整体思想,解答解三角形题
高中数学中解三角形题,主要运用三角函数与正弦、余弦定理.但是解答部分习题时,仅仅掌握三角函数相关知识并不能有效地求得正确结果.原因在于部分学习者在运算的过程中不注重整体思想的应用,计算过程中走了不少弯路.为避免学习者出现这一情况,应结合自身教学经验以及学习者的实际情况,为学习者做好借助整体思想解答三角函数习题的讲解.

解析该习题较为常规且难度不大.解题的关键具备整体思想应用意识,在整体思想指引下开展运算.另外,根据经验遇到求三角形的习题时,首先想到需要运用正弦、余弦定理实现边和角的互化.在此基础上对给出的已知条件进行整理,转化,并认真观察各关系式,运用整体思想降低计算难度.
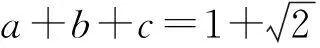
3 借助整体思想,解答不等式习题
“不等式”是高中数学较为基础的知识点,是高考的热门考点.部分习题技巧性较强,解题时若不能运用正确的解题思想便难以有效地切入.根据经验解答相关习题不仅要联系不等式的相关性质,以及相关运算公式,而且还应注重对已知条件进行适当转化.必要情况下,运用整体思想将其中的一部分看成一个整体,通过巧妙的代换减少参数的同时,直观地揭示出相关参数之间的联系,为更好地运用不等式相关运算公式奠定坚实基础.
例3已知a、b、c均为大于零的数,且满足a2+2ab+2ac+4bc=12,则a+b+c的最小值为____.
解析看到给出的参数均为正数,根据经验需要应用基本不等式知识.但是看到给出的已知条件,很多学习者因不会转化而一头雾水.事实上解答该题需要具有较强的观察以及分析能力,采用整体思想进行参数的巧妙代换,减少参数个数向基本不等式靠拢.

4 借助整体思想,解答向量习题
向量在高中数学中占有重要地位.其涉及的概念以及运算公式较多,且与其他知识点有着密切的联系,因此习题类型非常之多.部分习题以向量为背景考查学习者的运算能力.解答该类问题尤其不能走入出题人设计的陷阱之中,应注重保持清醒的头脑,通过整体思想的应用,将看似复杂的问题简单化,提高运算效率.

解析该题要求两个向量余弦的平方值,涉及的参数较多,计算量较大.如采用整体思想,可很好地简化计算,提高解题正确率.
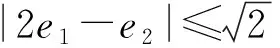
5 借助整体思想,解答导数习题
“导数”是高中数学的难点,是高考的必考知识点.部分习题难度较大,没有较强的综合能力,难以求解出正确结果.部分高中导数习题综合性较强,需要学习者灵活运用多种解题思想,尤其通过整体思想的应用,可确保问题得以顺利解答.

解析该题属于导数部分难度较大的题目.解题的关键在于等价转化,并运用整体思想化繁为简,而后借助导数知识以及函数图象,找到解题切入点.
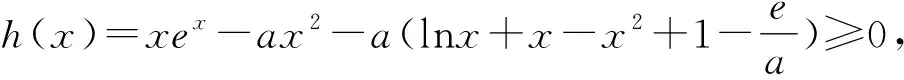
通过讨论不难得出,在很多的高中数学习题解答过程中都能看到整体思想的身影,整体思想在整个高中数学中的重要性不言而喻.高中数学教学实践中为使学习者认识、理解、掌握借助整体思想在解答不同数学习题时的相关技巧,在讲完数学理论基础后,应结合教学进度,通过相关例题为学习者做好应用性示范,将相关应用细节考虑到位,有效提升学习者的解题能力.
