多机吊放声呐搜潜航路规划建模仿真

2023-03-22段宇涵于兆磊朱智林肖来祥

物联网技术 2023年3期

段宇涵，于兆磊，朱智林，肖来祥

（1.山东工商学院，山东烟台 264005；2.烟台恩邦电子科技有限公司，山东烟台 264006）

0 引言

双机协同反潜可以实现快速对可疑海域搜潜，是直升机协同搜潜的作战样式之一。国内外有关反潜直升机携吊放声纳搜潜的相关研究较多[1-4]。其中，吴芳和罗木生等人[1-2]提出了一种双机方形拓展，得到了更高的搜潜概率；吴芳等人[3]建立了多种搜潜模型对其进行仿真分析；储林臻等人[4]提出了一种通用搜潜模型计算方法。本文从单机方形拓展改进为满足多机搜潜方案的阵型规划模型，根据不同目标指示信息计算潜艇散布概率，结合目标逃逸速度变化和吊放点数，分析该应召反潜模型的变化规律，并对阵型规划模型的实用性与可行性进行了研究分析。

1 多机协同拓展搜潜阵型建模

多机协同拓展搜潜方法的原理是以丢失潜艇目标的位置作为初始搜索位置[5]，根据潜艇已知信息的程度划分出一定范围的搜索区域，根据出动直升机的个数规划好搜潜路线，反潜直升机携带好吊放声呐后直接飞抵规划好的吊放点处，顺序执行任务。

根据直升机数量的不同和各个直升机携带吊放声呐装备探测性能的不同进行多机航路规划[6]。设潜艇目标最后发现位置为Ptag=(Xtag,Ytag)，航速为ptag，单位为km/h。假定有N架直升机参与吊放搜索（N=1, 2, 4），编号为Ni的直升机当前位置Heli=(Xi,Yi)，速度为Vi，单位为km/h，易得直升机与目标的距离为：

直升机前往目标位置用时：

在此时间内目标逃逸距离为：

如图1所示，直升机到达时目标概略位置为以目标初始位置Ptag为圆心、Lesc为半径的圆形区域内，称Lesc为目标的逃逸半径。在有多架直升机协同吊放搜索时，考虑到各直升机初始位置不同，飞抵目标用时不同，因此Lesc取各直升机飞抵时间平均值，则有：

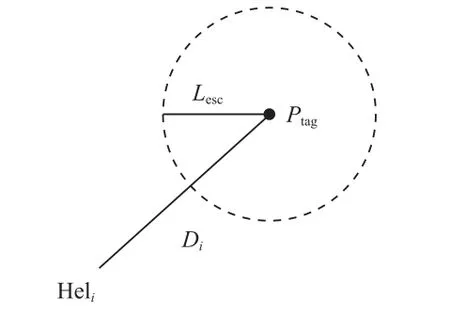
图1 逃逸半径的确定

考虑各直升机携带吊放声呐装备性能参数不同，设Ni直升机吊放声呐探测半径为Ri，N架直升机所携带声呐的最大探测半径为Rmax，单位为km。

已知逃逸半径Lesc，首个吊放点应设在距离目标Lesc的圆上。可确定最近机Helmin方向为αmin（Ptag为圆心，正北为0，采用弧度值，下同），方形搜潜阵型朝向确定为αmin，则首个吊放点角度可确定为：

设Pi(i=2, 4)为多机首个吊放点，现已知距离和角度，可求得该点。为寻找直升机飞抵任务点最短时间，通过排列组合将各机与各点距离和记为sumi(i=1, 2, 4)，取最小值为各机首个吊放点方案，如图2所示。

图2 双机搜潜首个吊放点的确定

假设有N架直升机参与吊放T层方形扩展阵，记当前层数为c(1≤c≤T)，间隔系数为coedip。当c=1时，方形边长为Lesc，此后每向外扩展一层，方形边长要增加2Rmaxcoedip，即第c层方形边长为：

在每层方形阵中，记每架直升机负责吊放的边数j=4/N，每条边有k个吊放点，k=Lc/Ri，第i架直升机的每层吊放初始点Pi1=(Xi1,Yi1)，则有：

在计算出每层吊放初始点后，又已知搜潜方向与各点间隔，可依次求出剩余吊放点。同时为避免重复探测，在计算完成后的实际探测中每架飞机都删除第一个探测点，如图3所示，由此多机协同拓展时的各吊放位置点可求得。

图3 协同拓展搜索示意图

为提高搜潜效率，考虑到吊放时间和潜艇逃逸时间，航路规划中的吊放点不是必需探测的，可根据应召反潜已知信息计算下个点的潜艇分布概率，若概率低于一定值，可选择跳过该吊放点。

2 应召搜潜模型

2.1 潜艇散布海域建模

潜艇散布海域的位置和形状与获知目标信息的多少有很大关系[7-11]。设获知潜艇目标应召点时刻为t0、反潜飞机到达应召点时刻为tarr，则潜艇运动时间tmove=tarr-t0，能明确潜艇散布海域的以下两种情况。

（1）潜艇航向未知，航速范围已知。设潜艇航速范围为[vmin,vmax]并服从均匀分布，则潜艇的可能分布范围是以潜艇应召点为圆心、内径为vmin(tarr-t0)、外径为vmax(tarr-t0)的圆环区域，搜潜面积为：

当潜艇航速为0、静止不动时，待搜潜海域是半径为vmax(tarr-t0)的圆形区域，将圆的外切正方形作为搜潜海域，则搜潜海域面积为：

（2）潜艇航向范围已知，航速范围已知。设潜艇航向范围[cbegin,cend]以正北为0°，顺时针从cbegin到cend，航速范围为[vmin,vmax]且航向航速均服从均匀分布。由此可得搜潜海域为一个完整圆环的一部分，圆心为潜艇初始位置，内径为vmin(tarr-t0)，外径为vmax(tarr-t0)，此时海域面积为：

其中，cbegin

2.2 潜艇目标位置分布

均匀分布和瑞利分布是航速未知时最常假设的两种情况[12,13]，下面将分别给出两种情况下的目标散布模型。

设潜艇的速度v服从于以σ为参数的瑞利分布R(σ)，航向θ服从[0, 2π)上的均匀分布，在极坐标下设位置为(r,θ)，则概率密度函数为[14]：

假设潜艇不知自己被发现，仍保持匀速直线运动，则其航向服从均匀分布[15]：

航速服从瑞利分布：

设潜艇运动t时间后的位置为(r1,θ1)，则服从分布：

设潜艇的速度v服从[vmin,vmax]上的均匀分布，由于潜艇航向范围已知，d为t时刻潜艇运动距离。潜艇当前位置

与初始位置的关系如图4所示。探测概率增加。

图4 潜艇当前位置与初始位置的关系

由此则有：

经由时间t后随机变量r0与r1的关系为：

航向和航速均为均匀分布情况下潜艇分布的概率密度为：

2.3 任务搜索概率

设反潜直升机在整个任务时期内累计探测N次，各吊放点的探测情况相互独立，每次探测概率为pi(i=1, 2, ...,N)，则该任务下总的发现概率为：

第n次探测时第一次发现目标的概率为[16]：

则一次任务下总的发现概率为：

3 仿真计算

仿真条件：假设潜艇初始应召点为坐标原点，位置误差为1.8 km；潜艇最小航速为9.26 km/h，最大航速为40 km/h，潜艇航速散布的标准差为2.6 km/h；潜艇初始航向在[0, 2π)内均匀分布；吊放声呐探测距离为12 km；吊放点重叠系数k=1.6；直升机留空时间为2.5 h；每个吊放点探测时间为10 min。

从图5可以看出，随着延迟时间的增加，探测概率降低；随着直升机平台的增加，探测概率增加。因为四机协同搜潜吊放点分布于方形海区的四个方向上，有超过单机、双机搜潜的重叠面积，增加了搜潜概率。从图6中可以看出，随着吊放次数的增加，探测概率增加；随着直升机平台的增加，