高速磁浮列车过隧道诱导的隧道出口列车风研究

成炯豪，郭易，郭迪龙，纪占玲，毛军，刘雯

1.中国科学院力学研究所 流固耦合系统力学重点实验室，北京 100190

2.中国科学院大学 工程科学学院，北京 100049

3.北京交通大学 土木建筑工程学院，北京 100044 4.中车工业研究院有限公司，北京 100070

0 引言

截至2021年底，我国铁路运营里程已经突破1.5×104km（其中高速铁路超过4×104km），且穿越山区的线路占比较高。列车在山区运行时，受限于牵引力及最大坡度要求，常需以穿隧方式克服高程障碍。列车高速进入隧道时，会产生以当地声速向隧道出口传播的压缩波[1]。列车速度低于当地声速时，压缩波先于列车到达隧道出口形成列车风。强烈的列车风会对隧道内外的铁路附属设施产生不利影响，并对轨旁工作人员安全构成威胁[2-5]。

磁浮轨道交通由于具有速域宽、爬坡强、噪声低、环保节能等方面的优势，在轨道交通中脱颖而出[6]，受到世界各国的广泛关注。我国在实现中低速磁浮列车量产的基础上，启动了200～600km/h高速磁浮列车研制项目[7]。高速磁浮列车速度更快，压缩波强度更大，在隧道出口诱导的气流突变更加显著。为在我国铁路线路多隧条件下实现高速磁浮列车的安全运营，需要对高速磁浮列车通过隧道时诱导的列车风特性进行深入研究。

日本新干线投入运营后，国内外研究者对高速列车隧道气动效应开展了一系列研究[8]。在理论研究方面，李炎等[9]探讨了列车长度、隧道长度、阻塞比等因素对活塞风的影响，提出了活塞风压力和活塞风速度的计算方法；Howe 等[10]基于相似理论试验研究了隧道内压缩波对隧道出口微气压波的影响规律，提出了列车进入隧道产生的压缩波的解析模型；顾红生等[11]从空气动力学基本方程出发，推导了按非定常流计算活塞风速度的理论公式，分析得出了影响隧道内活塞风速度的主要因素为列车速度和隧道截面积。这些理论结果大多是在早期有限的计算机技术条件下根据一维简化模型推导得出，可以为列车风研究提供理论指导，但列车在隧道内的实际气动效应是复杂的三维瞬态流动，对于列车通过隧道全过程的多维模拟，理论研究存在较大困难[12]。

在实车实验方面，Sakuma 等[13]基于实车实验研究了隧道内列车风；刘峰等[14]测试了高速动车组穿越双线隧道引发的隧道壁面气动压力，分析了列车通过和驶出阶段不同位置测点的压力峰值；方雨菲等[15]基于现场测试分析了不同因素对隧道附属设施表面气动荷载、振动加速度和列车风速度的影响，给出了隧道内气动荷载分布规律；刘堂红等[16]对隧道中列车诱导的列车风进行了现场测量，发现列车风速度与列车运行速度呈线性关系。

实车实验大多针对车速较低的传统轮轨列车，实施难度大、成本高，因此，数值模拟在高速列车气动效应研究中得到了广泛应用。梅元贵[17]采用数值方法分析了高速铁路隧道压力波的传播特性；牛纪强[18]对不同编组长度的列车以不同速度通过隧道和隧道内交会进行了分析研究，发现列车尾流引起的列车风速度最高，编组长度对列车风影响显著；王磊等[19-20]采用数值方法模拟了CRH380A 高速列车通过双线隧道的全过程，研究了双线隧道内的列车风分布及流场特性；朴荣焕等[21]对地铁车辆通过隧道的动态过程进行了数值模拟，研究结果表明隧道内活塞风主要为纵向流，距离车身越远，活塞风峰值速度越低；管鸿浩等[22]对单列列车通过双线隧道引起的列车风分布规律进行了研究，结果表明：由于列车与隧道壁之间空隙不均匀，导致列车两侧列车风峰值速度出现于不同时刻。在上述研究中，国内外研究者对临近列车车身的流动多有关注，而对压缩波诱导的隧道出口列车风关注较少。

本文通过与动模型实验的对比，验证了隧道出口列车风数值计算结果的准确性。以高速磁浮列车作为研究对象，采用数值方法研究了列车运行速度、隧道阻塞比对隧道出口列车风的影响规律。

1 计算方法与模型

1.1 计算方法

使用Simcenter STAR–CCM+对磁浮列车通过隧道的过程进行计算。对三维、可压缩、非定常N–S 方程进行求解：

为使方程封闭，还需补充完全气体状态方程：

式中：ρ、p、t 分别为密度、压力和时间；x、u 分别为坐标和速度，下标i、j、k 表示3 个方向的分量；e 为单位质量气体的内能，δij为克罗内克符号，µ为黏性系数，k 为热传导系数，T 为温度，γ为比热比，R 为气体常数。采用SST k−ω湍流模型，方程中对流项的离散采用Roe 格式，黏性项的离散采用二阶中心差分方法，时间上采用二阶隐式方法进行积分，时间离散采用带伪时间步的LU–SGS 方法。

以重叠网格作非定常计算，若1 个时间步内列车运动距离与重叠区域背景网格尺寸相差过大，计算不收敛。1∶8 缩比模型计算时间步长取6 × 10−4s，实车模型计算时间步长取2 × 10−3s，1 个时间步内列车运行距离不超过2 个重叠区域背景网格，内迭代步数均为5，满足内迭代残差下降一个量级。

目前，近壁湍流处理有两种方法：直接求解到壁面和采用壁面函数。本文计算模型为1∶1 真实外形磁浮列车，其外部流动为复杂三维流动，总网格量相当大。为控制网格数量，本文参考相关文献的处理方法[23-24]，采用标准壁面函数对近壁湍流进行处理。

1.2 计算工况

列车运行速度是影响压缩波强度的重要因素。本文以高速磁浮列车为研究对象，列车运行速度为400、500 和600 km/h。当隧道截面积、列车运行速度和列车长度确定后，最不利隧道长度随列车运行速度增大而减小，当列车运行速度为400 km/h 时，最不利隧道长度约为404 m[25]。此外，本文研究重点为列车进入隧道后的压缩波在隧道出口引起的列车风，压缩波以当地声速传播，若隧道长度过短，将难以区分列车附近活塞风引起的风速和压缩波诱导形成的风速。综合以上两点考虑，将隧道长度设定为500 m，以满足避开最不利隧道长度以及压缩波迟于列车到达隧道出口1 s 以上的条件。

隧道阻塞比也是影响压缩波强度的主要因素之一。由于目前尚无高速磁浮列车工程化线路，本文采用文献[26]中的单线隧道模型（隧道出口无缓冲结构，隧道截面积为70 m2），经等比例放大得到隧道截面积为90 和110 m2的单线隧道，对隧道阻塞比与压缩波诱导隧道出口列车风的关系进行了研究。

1.3 模型与计算域

基于磁浮列车实车模型（图1）进行数值计算。全车长130.7 m（含车间间隙），高约4.2 m，宽约3.7 m；共5 节车厢，头（尾）车长约28.08 m，中间车单节长约24.52 m。计算域包括隧道及其两端外场，两端外场尺寸相同。隧道和计算域参数如图2所示。

图1 磁浮列车模型Fig.1 Maglev train model

图2 隧道和计算域参数示意图Fig.2 Schematic diagrams of the tunnel and the computational domain

1.4 网格与边界条件

使用重叠网格方法进行计算。该方法适用于模拟对象存在边界运动的情况，可以真实模拟列车与隧道之间的相对运动。网格模型包括背景网格和部件网格：背景网格是整个计算域网格，部件网格为车身附近的一部分流体空间网格。如图3所示：红色虚线框为背景网格的加密区域，网格尺寸为0.250 m；蓝色虚线框为车身网格与背景网格的重叠区域，网格尺寸为0.125 m。部件网格与背景网格之间重叠4～5 层网格，确保流场数据交换足够准确，网格总数约为1 500 万。

图3 计算域网格Fig.3 Computational gird

边界条件包括压力出口和无滑移壁面，隧道壁面及计算域地面设置为无滑移壁面条件，其他计算域边界设置为压力出口条件。包含列车的overset 区域设置为运动条件，通过给定该区域的速度实现列车的运动。

2 算例验证

2.1 算法验证

动模型实验是目前列车风测试最为有效的手段[1,26]，可通过实验结果验证数值方法的准确性。本文将1∶8 缩比列车模型数值模拟结果与动模型实验结果进行了对比。缩比列车模型数值模拟所用体网格尺寸为实车模型体网格尺寸的1/8，采用第1 节介绍的计算方法。标准列车模型（全长10.084 m）设计引入了VMF 参数化方法，通过控制头型长度、排障器外形、驾驶室前挡玻璃外形、头型纵剖面型线等生成头车模型，能够反映高速列车外形且可重复实现。隧道由横截面积S=70 m2的单线隧道等比例缩小得到，长度为60 m。

动模型实验在中国科学院力学研究所的高速列车双向动模型平台上进行。以固定于隧道出口平面处的一维热线风速仪测量风速，如图4所示。热线风速仪与轨道中心线的距离以及与轨道顶面的高度差遵照TSI 和EN-14067[25]的标准：距离轨道中心线375 mm，高于轨道顶面25 mm（对应实车距轨道中心线3.0 m，高于轨道顶面0.2 m）。隧道置于动模型平台测试段内，列车在平台测试段范围内以近似匀速的状态滑行。数值模拟中，在与动模型实验相同的位置布置测点测量风速。

图4 热线风速仪安装位置Fig.4 Installation position of the hot wire anemometer

要获得列车某一运行速度下隧道出口的列车风特征，需对该速度下多次列车风测试结果取系综平均值，获得系综平均曲线，并基于系综平均曲线研究该速度下的隧道出口列车风特征。图5 给出了列车速度200 km/h 时的动模型实验数据（黑色虚线表示头车到达隧道入口，红色虚线表示头车到达隧道出口）。可以看到，在头车到达隧道出口前，单次试验和系综平均的列车风速度曲线基本重合，说明压缩波诱导的气流流场稳定，实验可重复性较高。需要说明的是：在滑行过程中，列车受到轨道摩擦阻力和气动阻力，作加速度很小的减速运动，实验用时约1.10 s，而理论上匀速通过隧道所需时间约为1.08 s。

图5 隧道出口列车风速度Fig.5 Wind speed at the tunnel exit

对比了动模型实验和数值模拟的结果（列车运行速度为200、250 和300 km/h）。头车到达隧道出口时的测点列车风速度由车身绕流形成，风速变化剧烈，且本文重点关注头车未到达隧道出口时由压缩波诱导的隧道出口风速，故仅选取头车到达隧道入口至头车到达隧道出口这一时间段内的列车风速度曲线进行对比，如图6所示。图6 中的实验结果和数值模拟结果吻合较好。需要说明的是：动模型实验平台轨道下方及隧道接缝处存在缝隙，隧道密封性比理想条件差；数值模拟则是完全密封的理想条件，故两者隧道内压缩波和膨胀波的强度略有差异，在风速曲线的波峰和波谷处，实验结果与数值模拟结果存在一定误差。

图6 不同列车运行速度下的动模型实验和数值模拟测点风速对比Fig.6 Comparison of wind speed at the measuring point between moving model test and numerical simulation

2.2 网格无关性验证

为验证计算结果与网格尺寸的无关性，对磁浮列车实车模型进行了网格无关性计算。设计了3 种加密区体网格尺寸进行计算和对比：在粗网格方案中，加密区体网格尺寸为0.500 m，总量为700 万；在中网格方案中，加密区体网格尺寸为0.250 m，总量为1 500 万；在细网格方案中，加密区体网格尺寸为0.125 m，总量为2 300 万。

在隧道长度500 m、列车运行速度400 km/h 工况下，对比3 种网格方案下计算得到的隧道出口风速，如图7所示：中网格和细网格方案风速曲线的峰值和变化趋势基本一致，而粗网格方案的结果与其他两种方案存在一定偏差。为保证计算精度、节约计算资源，选择加密区体网格尺寸为0.250 m 的中网格方案进行后续计算。

图7 不同网格尺寸下的隧道出口风速Fig.7 Comparison of wind speed under different grid resolution conditions

3 结果分析

列车运行速度、隧道阻塞比对压缩波强度的影响较大。本文设计了400、500 和600km/h等3 个速度以及70、90 和110 m2等3 种隧道截面积。首先对隧道出口附近压缩波诱导列车风的空间特性进行分析，然后探讨列车运行速度和隧道阻塞比对压缩波诱导隧道出口列车风的影响。本节所涉及的速度均为空间3 个方向的合速度。

3.1 压缩波诱导隧道出口列车风特性

以列车运行速度400 km/h、隧道长度500 m、隧道截面积70 m2为例，对隧道出口列车风特性进行分析。图8 上图为隧道内的压缩波和膨胀波传播图，图8 下图为隧道出口平面距离轨道中心线3 m、高度1.5 m 处（z=1.5 m）测点的风速曲线。

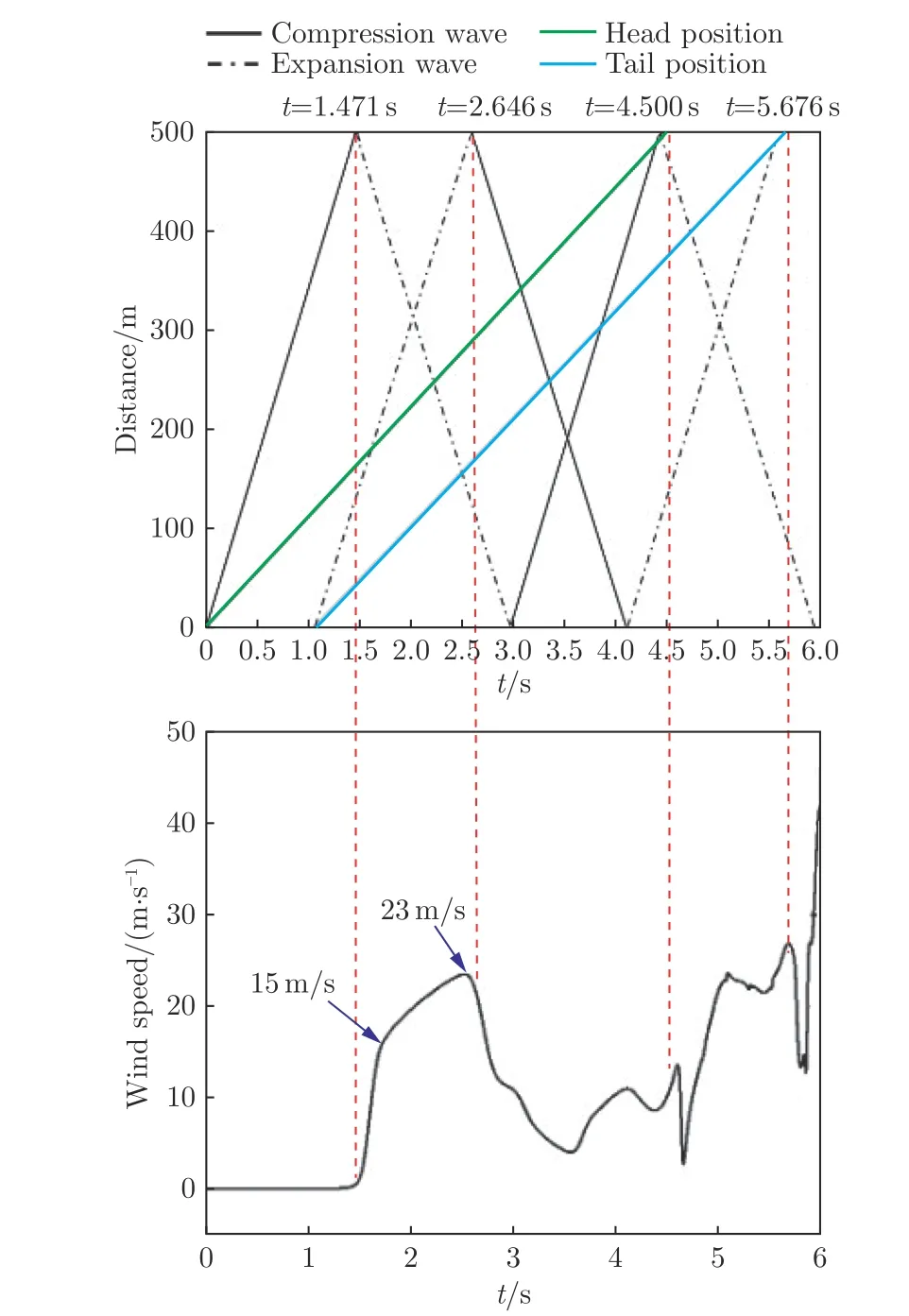
图8 隧道内马赫波传播图及隧道出口测点风速Fig.8 Mach wave propagation in the tunnel and wind speed of the measuring point at the tunnel exit

头车鼻锥到达隧道入口时（t=0 s），初始压缩波形成，并以当地声速向隧道出口传播；t=1.176 s 时，尾车鼻锥到达隧道入口，产生膨胀波，并以当地声速向隧道出口传播；初始压缩波和膨胀波分别于t=1.471 s 和t=2.646 s 到达隧道出口测点位置。从图8 可以看出：当初始压缩波到达测点位置，测点风速突然快速增大至15 m/s，这是由头车进入隧道后的初始压缩波所导致；随着车身驶入隧道的长度增加，测点风速在列车车身波作用下缓慢增大至峰值23 m/s（相当于9 级大风）；当初始膨胀波到达测点位置，测点风速开始大幅下降；t=4.500 s 时，头车鼻锥到达隧道出口，测点风速（主要由车身绕流导致）突然波动后逐渐增大；t=5.676 s 时，尾车鼻锥到达出口，测点风速在列车尾流影响下先减小后增大。

需要指出的是：初始压缩波诱导形成隧道出口列车风时，列车头车距离出口尚远，这意味着在高速磁浮列车通过隧道过程中，不仅需要关注列车临近时的气流流动，还需要高度关注列车距离很远时由压缩波诱导形成的隧道出口列车风；尤其是当隧道较长时，压缩波诱导形成隧道出口列车风达到峰值与列车到达隧道出口的时间差更大，更需提前预警。下文对头车到达隧道入口至头车到达出口这一时间段内的隧道出口列车风特性进行研究。

在隧道出口附近布置测点，监测列车通过隧道过程中列车风速度的空间分布。首先，对隧道出口不同方位的风速分布进行研究，测点1～5 位于隧道出口平面，坐标如图9（a）所示；其次，对列车风速度的纵向（x 方向，列车运行方向为正）和横向（y 方向，垂直于列车运行方向）空间分布进行研究，测点位置如图9（b）所示（纵向范围从隧道出口内25 m 至隧道出口外25 m，相邻测点间隔5 m；横向范围从轨道中心线至距轨道中心线5 m 处）。目前尚无相关标准依据设定测点高度，各测点高度暂设定为1.5 m，对应列车底板高度。

图9 测点分布Fig.9 Distribution of the measurement points

头车到达测点1～5 所在的出口平面（t=4.5 s）之前，各测点由压缩波诱导的风速变化趋势与幅值基本相同，如图10所示。这是由于压缩波在隧道内以近似一维波阵面的方式传播，隧道内同一垂直截面上不同方位的压缩波强度几乎相同，隧道出口不同方位由压缩波诱导的列车风速度无明显差异。

图11 为轨道中心线（y=0）上测点风速随时间的变化曲线。可以看到：头车到达隧道出口之前，隧道内各测点风速无明显差异；在隧道出口外，压缩波向四周扩散，强度降低，随着隧道外测点与出口距离的增大，由压缩波诱导形成的列车风速度增幅及峰值均逐渐降低，隧道出口外5 m 处的列车风峰值速度约为20 m/s，25 m 处则已降至9 m/s。对比隧道内外测点风速曲线的形状，可以看到，隧道内测点风速呈“两段式”增长：车头进入隧道产生的初始压缩波会导致隧道出口风速骤增；随着车身继续驶入隧道，风速缓慢增加至峰值。而隧道外测点风速在初始压缩波到达后，风速的增长趋势未有明显分段，以几乎不变的增幅增大至峰值。

图11 轨道中心线上测点风速Fig.11 Wind speed at the measuring points of track center line

对隧道出口外横向范围内的测点风速进行对比。如图12所示，从出口外x=5、15 和25 m 的测点风速可以看到，在y <5 m 范围内，风速变化趋势与峰值相差较小。这一结果表明，列车高速通过隧道时，在距离轨道中心线5 m 的横向范围内，压缩波诱导的隧道出口列车风速度基本保持不变。

图12 不同y 坐标下的列车风速度对比Fig.12 Comparison of wind speed at different y

图13 为不同时刻隧道出口附近的速度云图（z=1.5 m）。t=1.5 s 时，压缩波到达隧道出口，隧道内风速增至7 m/s，此时出口外受压缩波影响的范围较小。随着压缩波不断诱导气流向出口外扩散，t=2.0 s 时，隧道内风速增大至约20 m/s，隧道外受压缩波影响的范围在横向上扩大至轨道中心线两侧10 m 处，纵向上扩大至出口外6 m。t=2.5 s 时，隧道内测点风速达到峰值23 m/s，出口外受压缩波影响的范围在横向上无明显变化，在纵向上则扩大至13 m。从压缩波到达出口至出口风速达到峰值这一时间段内，压缩波在隧道外仅对出口局部区域气流产生影响。这是由于压缩波在隧道出口外以微气压波形式向四周扩散，强度迅速降低，由于不再受限于隧道壁，一段距离后气流速度迅速降低。

图13 不同时刻隧道出口的速度云图Fig.13 Velocity contours at different times near the tunnel exit

3.2 车速对压缩波诱导隧道出口列车风的影响

由前文分析可知，隧道内不同位置的压缩波强度相同。以隧道出口内5 m 处（x=−5 m）轨道中心线上的测点为例，对不同列车运行速度下隧道内压缩波诱导的列车风进行分析（隧道截面积为70 m2，阻塞比为17.04%）。图14 为头车到达隧道入口至头车到达隧道出口这一时间段内的风速曲线。

图14 隧道出口内测点风速Fig.14 Wind speed at the measurement points in the tunnel

从图14 可以看到，3 个速度下的风速曲线变化趋势基本一致。t=1.47 s 时，初始压缩波达到测点位置，测点风速突然急剧增大。车速400 km/h 时，压缩波诱导的列车风峰值速度为23 m/s，相当于9 级大风；车速增至600km/h时，列车风峰值速度高达56 m/s，相当于3 级飓风：车速由400 km/h 增至600 km/h，列车风速度增大了约140%。

图15 为不同车速下隧道出口外轨道中心线上各测点由压缩波诱导的列车风峰值速度对比。可以看到，在隧道出口外5 m 处（x=5 m），由压缩波诱导的列车风速度与隧道内的速度大小相近。在隧道出口外纵向25 m 的范围内，压缩波诱导的列车风速度在不同车速下的降低幅度不同：车速400 km/h 时，列车风峰值速度由20 m/s 降至9 m/s，降低约55.00%；车速500 km/h 时，峰值速度由35 m/s 降至26 m/s，降低约25.71%；车速600km/h时，峰值速度由56 m/s 降至47 m/s，降低约16.07%。随着车速增大，风速降低幅度逐渐减小。这就意味着，磁浮列车高速通过隧道时，隧道出口外的纵向危险范围会随着车速增大而大幅增大。

图15 隧道出口外测点列车风峰值速度Fig.15 Maximum wind speed at the measurement points outside the tunnel

3.3 隧道阻塞比对压缩波诱导隧道出口列车风的影响

隧道阻塞比也是影响隧道内压缩波强度的重要因素之一。在隧道截面积为70、90 和110 m2的工况下进行了计算（列车运行速度为600 km/h，列车截面积约为11.93 m2），3 种工况对应的隧道阻塞比分别为17.04%、13.26%和10.82%。以隧道出口内5 m处（x=−5 m）的测点为例，对隧道内的列车风速度随阻塞比的变化进行分析，如图16所示。t=1.47 s 时，初始压缩波到达隧道出口，t=3.0 s 时，列车头车到达隧道出口。从这一时间段内测点风速的峰值可以看出：在不同阻塞比下，由压缩波诱导的列车风峰值速度不同，随着阻塞比增大，测点峰值速度增大，阻塞比增大6.22%，峰值速度由33 m/s 升至56 m/s，增幅高达67%。

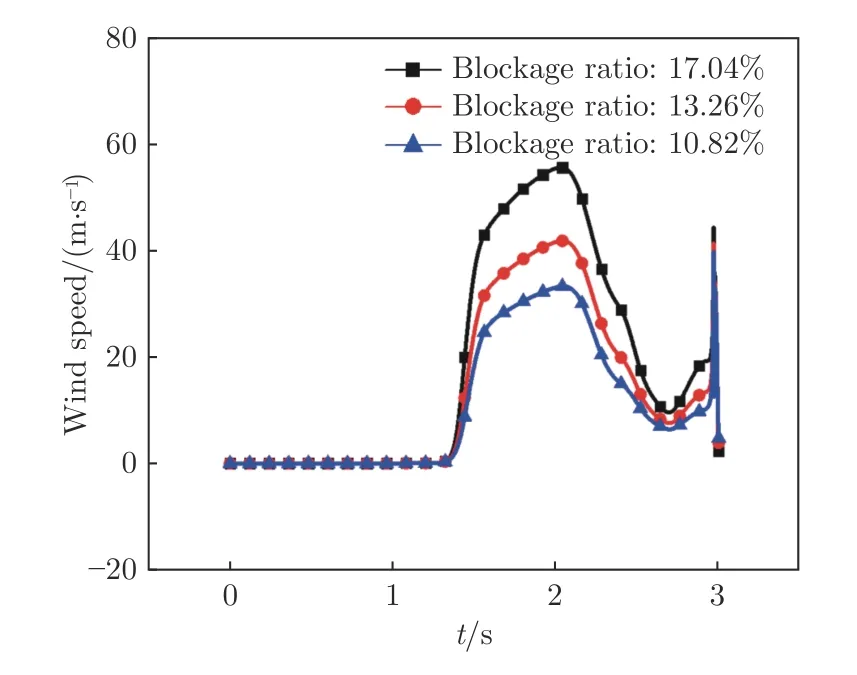
图16 隧道出口内测点风速Fig.16 Wind speed at the measurement points in the tunnel

对比不同阻塞比下、隧道出口外轨道中心线上各测点由压缩波诱导的列车风峰值速度，如图17所示。可以看到，在纵向25 m 范围内，随着测点位置逐渐远离隧道出口，压缩波诱导的列车风峰值速度逐渐降低，阻塞比越低，峰值速度降幅越大：阻塞比为17.04%时，峰值速度由56 m/s 降至47 m/s，降低约16.07%；阻塞比为13.26%时，峰值速度由37 m/s降至15 m/s，降低约59.46%；阻塞比为10.82%时，峰值速度由28 m/s 降至7 m/s，降低约75.00%。值得注意的是：阻塞比为17.04%时，隧道出口外25 m处测点由压缩波诱导的列车风峰值速度高达40 m/s，相当于13 级大风，对轨道附近作业人员和附属设施存在巨大威胁。

图17 隧道出口外测点列车风峰值速度Fig.17 Maximum wind speed at the measurement points outside the tunnel

4 结论

本文针对高速磁浮列车通过隧道过程中由压缩波诱导的隧道出口列车风开展研究，得到以下结论：

1）在列车到达隧道出口之前，压缩波会在隧道出口诱导形成强烈的列车风。初始压缩波到达隧道出口时，列车风速度突然开始增大，初始膨胀波到达隧道出口时，风速达到峰值并开始下降。

2）在隧道内的不同位置，压缩波诱导的列车风速度随时间的变化趋势与幅值基本一致。在隧道出口外纵向25 m 范围内，距隧道出口越远，由压缩波诱导的列车风峰值速度越低，在横向5 m 范围内则基本保持不变。

3）随着列车运行速度增大，隧道出口处由压缩波诱导的列车风峰值速度明显增大。在阻塞比为17.04%工况下，当车速由400 km/h 增至600 km/h，隧道内列车风峰值速度由23 m/s 增至56 m/s，隧道外纵向25 m 处峰值速度由9 m/s 增至47 m/s；随着车速增大，隧道外纵向25m 范围内峰值速度的降幅逐渐减小。

4）随着阻塞比增大，隧道出口处由压缩波诱导的列车风峰值速度明显增大。在车速600km/h工况下，当阻塞比由10.82%增至17.04%，隧道内列车风峰值速度由33 m/s 增至56 m/s，隧道外纵向25 m处峰值速度由7 m/s 增至47 m/s；随着阻塞比增大，隧道外纵向25 m 范围内峰值速度降幅逐渐减小。