基于粒子群与聚类的多目标优化算法

熊志坚, 王晓晶, 杨景明, 王伟芳, 赵志伟

(1.唐山学院 人工智能学院 河北省智能数据信息处理与控制重点实验室,河北 唐山 063000;2.燕山大学 电气工程学院,河北 秦皇岛 066004; 3.开滦总医院 信息科, 河北 唐山 063000; 4.唐山师范学院 数学与计算科学学院,河北 唐山 063000)

1 引 言

现实生活中的许多优化问题包含多个需要优化的相互冲突的目标[1]，这些问题被称为多目标优化问题(multi-objective optimization problems,MOPs),如数学、工业和商业等方面[2～4]。因此,多目标优化领域吸引了许多研究人员利用群算法开发一种高效、有效的优化算法,以期解决各种复杂问题[5]。粒子群算法收敛速度较快,但对于多目标优化而言,保持群中粒子的多样性一直是一个挑战。[6]。最优解的选择对于任何多目标粒子群优化(particle swarm optimization,PSO)都是至关重要的,需要加强个体非支配性的同时,并保持它们之间的多样性[7]。当处理MOPs时,因为几个目标相互冲突,无法使用关系运算符来比较解的优劣[8]。最终目标不是寻找一个单一的解,而是寻找一组均匀分布靠近帕累托前沿(pareto-optimal front,POF)的最优解[9]。PSO算法在处理MOPs时是通过探索和开发来实施。算法面临的主要挑战是需要在探索和开发之间取得平衡[10]。研究人员试图用当前优化代数与最大优化代数的比例来控制优化过程[11]。在优化过程中,种群成员的多样性减少了,因为PSO算法将引导当前的粒子移向目前为止找到的最佳解的位置[12]。因此,当前粒子越接近最优解,多样性越小。然而,解决MOPs需要种群的高度多样性,直到涵盖所有可行解[13]。

为多样化优选全局最优解,提出1种基于粒子群和分解聚类相结合的多目标优化算法(CDPSO)。种群与参考向量进行关联,对每个参考向量附近的解进行聚类,并使用聚合函数从每个聚类中只选择1个最优解。对于参考向量没有关联个体时,将从附近聚类中选择1个尚未选择的具有最小聚合函数值的解。优选个体被用来更新全局最优解。

2 相关理论

2.1 粒子群优化算法

粒子群算法由1个随机初始化的种群组成。寻找优化问题的每个解被当做粒子,所有粒子在目标空间中搜索。每个粒子有适应度函数值来判断自身位置的优劣。粒子能记录自身在搜索过程中的位置信息。粒子的速度决定自身的方向。粒子之间的位置信息共享,粒子不断调整本身的速度和位置往最佳的地方搜索。随着搜索的进行,种群生成全局最优解和个体最优解。最优解可以用于粒子速度和位置的更新。这些最优解引导粒子群算法探索优化问题的搜索空间。

第i个粒子的速度和位置更新公式分别为:

通过评估每个粒子的新位置,更新全球最优解和个体最优解。

2.2 参考向量

为了保持种群的多样性,使用基于参考向量的多目标优化框架,通过参考向量对目标空间进行分解,对种群进行聚类,然后利用这些参考向量选择最优解。通过Das和Dennis的系统方法在单位超平面上生成1组参考点,并绘制从原点到这些参考点的直线[14]。这些参考点放置在1个归一化的超平面上,该平面与所有目标轴倾斜,并在每个轴上有1个截距。参照点的数量为:

R=C(m+b-1,b)

式中:m为目标数量;b1和b2分别为目标轴上外层和内层等分截距数量。图1展示了当b=4时，在三目标(f1,f2,f3)空间总共生成了15个参考点。

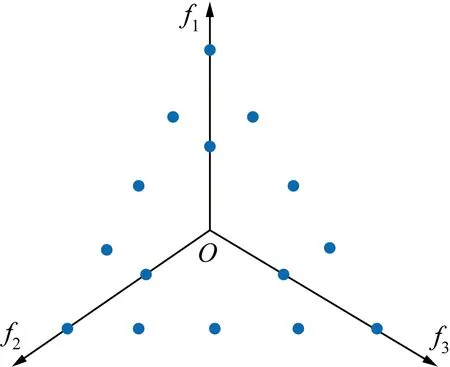
图1 参考点示例Fig.1 Reference point example

3 CDPSO

3.1 总体框架

CDPSO的总体框架算法如下:

1)p←初始化粒子群

2)V←初始化参考向量

3)p←归一化

4) whilet≤tmaxdo

5)p←聚类

6)gb,i,gb,i←p

7)更新粒子群中每个粒子的速度和位置

8)Q←对种群p实施交叉和变异操作

9)p←p∪Q

10)t=t+1

11) end while

12) returnp

首先,确定算法最大迭代次数,随机初始化N个粒子的种群,根据第2.2节内容在目标空间中产生均匀的参考向量。对种群归一化:

进行迭代,直到迭代次数达到规定的最大次数为止。把粒子中的全局最优解和个体最优解放入2个外部存档中,并更新粒子群中每个粒子的速度和位置。为了避免算法陷入局部最优,使全局最优解引导种群均匀分布在POF附近,需对当前种群P中粒子进行交叉[15]和多项式变异[16]操作,产生新的子代Q和父代种群相结合在一起。然后第t代的计数器增加1。最后,返回种群。

3.2 聚类

CDPSO中采用了基于参考向量的多样性策略。该方法的主要任务是更新全局最优解,并分配给每一代种群中的粒子,引导种群多样化均匀分布。聚类过程以参考向量为中心,通过计算粒子与参考向量的距离,具有最小D(p,V)值的粒子聚类到一起。参考向量与粒子之间的距离为:

生成聚类后,在每个聚类中选取1个具有最小聚合函数值F(p)的粒子,聚合函数表示如下:

F(p)=d(p,V)+λD(p,V)

图2所示为聚类过程。在两维目标空间中分布着5个参考向量(V1,V2,…,V5)和10个粒子(P1,P2,…P10),生成5个聚类,选取5个最优解。以参考向量V1为中心的聚类由粒子(P1,P2)构成,(P3,P4,P5)形成聚类V2,(P6,P7,P8)形成聚类,V4,(P9,P10)形成聚类V5。一旦形成了这些聚类,使用聚合函数从每个聚类中只选择一个优秀粒子,聚类V1中选择粒子P1,同理,粒子(P4,P7,P10)被选中。因为以上粒子分别在自己的聚类中具有最小的F(p)值。

参考向量V3并没有粒子与它关联,需要通过计算附近粒子与V3的聚合函数,找到具有F(P)最小值的个体完成聚类。最终聚类结果如图3所示,5个聚类通过聚合函数分别优选出5个最优解。

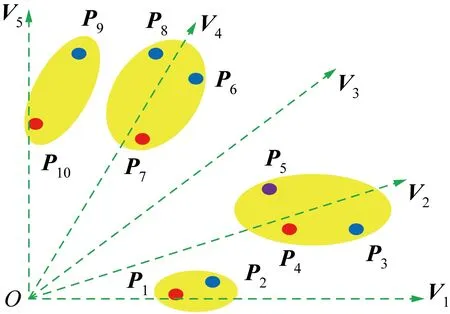
图2 聚类过程Fig.2 Clustering process

图3 最优解生成Fig.3 Optimal solutions generation

3.3 粒子更新

CDPSO充分利用了基于参考向量的算法所具有的高收敛性和高多样性的优点。

在优化过程中,从gb,i的存档中为群中的每个粒子分配一个全局最优解。由于CDPSO采用了多样性方法来分配全局最优解,因此将任务划分为两种情况。如果以每个参考向量为中心的聚类中,有一个粒子被优选,它将作为全局最优解分配给种群中属于这个参考向量的聚类中的粒子。为了避免下次重复选择,并将这个粒子在这个聚类中删除。如果参考向量没有粒子与它关联,将从它附近其它聚类中通过聚合函数选择一个最优粒子作为这个聚类的全局最优解,并从其它聚类中删除这个粒子。

gb,i的存档使用聚合函数来更新,如果粒子群中粒子本身的适应度值优于其个体最优解,则更新它为该粒子的个体最优解。

4 实验研究与分析

为了评估CDPSO算法的有效性,使用WFG[17]测试函数上对CDPSO算法与4种PSO算法(MMOPSO[18],MOPSO[19],SMPSO[20],dMOPSO[21])进行仿真实验。

4.1 参数设置

4个对比算法的参数值按照其原文的建议进行设置值。其它参数设置为:1) 种群总体大小为100,即随机产生的解的数量。2) 所有算法的迭代次数设置为10 000次。3) 每个算法都经过20次独立运行进行评估。4) 所有算法根据Wilcoxon符号秩检验对其评价结果进行了5%显著性水平检验。5) 在实验过程中,各算法在目标数量为(3,6,9)上分别测试。

4.2 性能指标

4.3 实验分析

所有算法在9个WFG测试问题中所获得的结果分别展示在表1中。表1包含了每个算法在20次独立运行中获得的IGD值的平均值和标准差,最优值加粗突出显示,括号内数据为标准差。Wilcoxon检验结果用符号(+,-,=)表示。符号“+”表明对比算法的性能明显优于CDPSO算法,符号“-”表示对比算法性能明显差于CDPSO算法,“=”表示2种算法性能相当。

表1 5个PSO算法获得的IGD平均值和标准差值Tab.1 The IGD average and standard deviation obtained by five PSO algorithms

由表1可以看出,CDPSO性能出色,在27个测试结果中,CDPSO获得的最佳IGD值达到20个,胜过MMOPSO达20项,全部优于MOPSO,胜过SMPSO和dMOPSO多达22项。IGD指标用来衡量每个算法获得的最优解与POF的距离,因此CDPSO是最接近POF的算法。

WFG1问题是1个混合和有偏差的问题,MMOPSO获得了所有目标的最佳IGD值。WFG2是1个凸的、不连接的、多模态的、不可分离的问题,在这个问题上,CDPSO获得了3目标和6目标上的最优值,MMOPSO获得了9目标上的最佳IGD值。WFG3问题是1个线性、退化和不可分离的问题,SMPSO获得了6目标和9目标上测试的最佳IGD值。WFG4问题是1个凹的多模态问题;WFG5问题是1个凹的欺骗问题;WFG6问题是1个凹的不可分离问题;WFG7是1个凹的、偏向的问题;WFG8是1个凹的、偏向的、不可分离的问题;WFG9是1个凹的、偏向的、多模态的、欺骗性的、不可分离的问题。CDPSO在WFG4-WFG9多个目标测试中,全部获得了最优值。

为了更加直观地展示CDPSO算法的优势,5种PSO算法在3目标WFG6测试问题上获得的最优解展示在图4中。从图4可以看出,MMOPSO,MOPSO和SMPSO三个算法的最优解并没有收敛到POF附近,并且分布不均匀。dMOPSO算法陷入了局部最优,最优解集中到1个角落中。CDPSO算法的最优解均匀的收敛在POF附近,表明聚类更新全局最优解的策略产生了良好的作用。

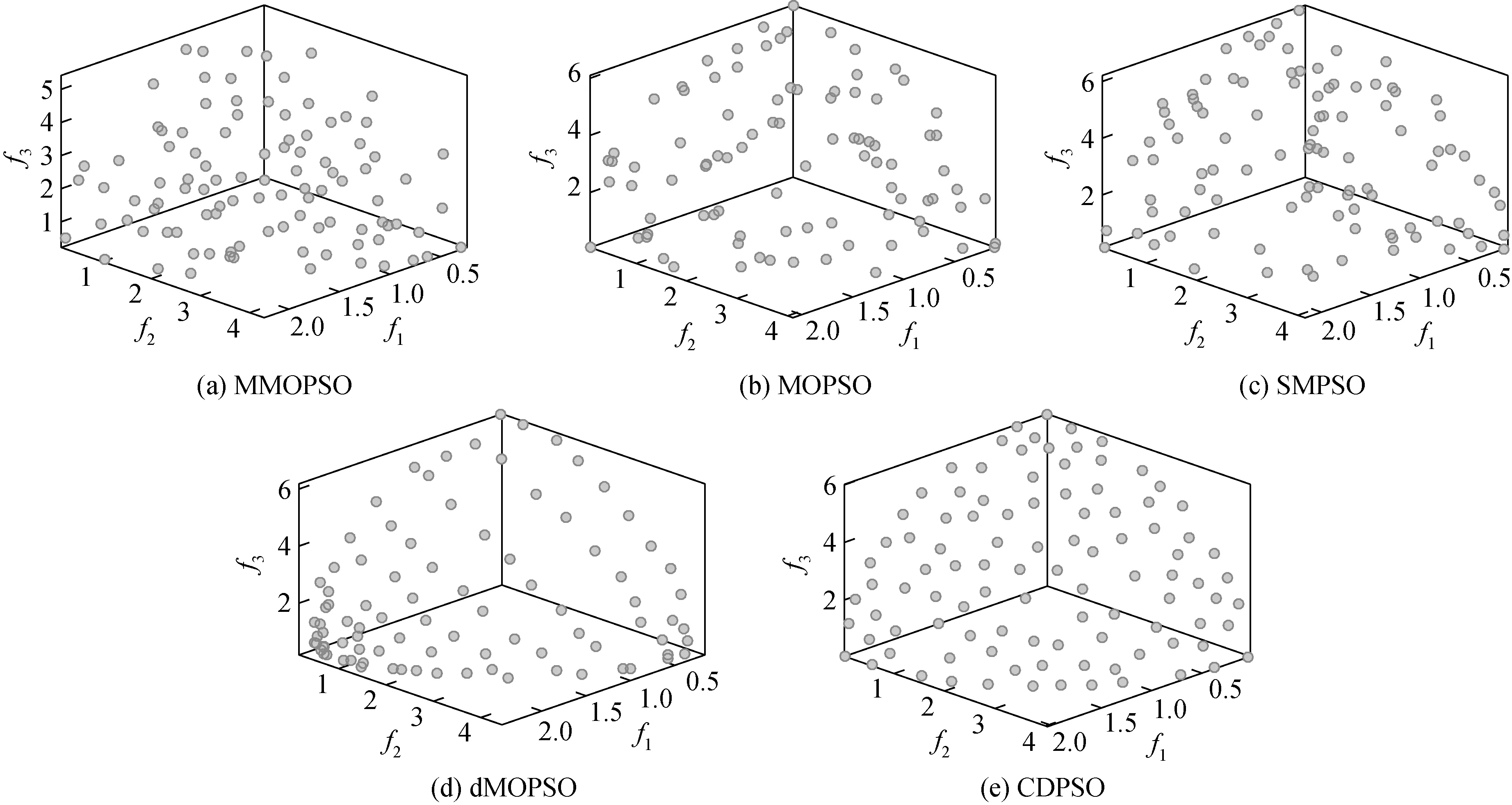
图4 5个PSO算法在3目标WFG6测试问题上获得的最优解Fig.4 The optimal solution obtained by five PSO algorithms on the 3-objective WFG6 test problem

5 结 论

利用参考向量分解聚类,结合多目标粒子群优化算法,提出了基于粒子群的多目标优化算法。该算法主要目标是增加最优粒子的多样性选择,用于更新全局最优解。在WFG测试问题上对CDPSO算法和4个PSO算法进行了性能比较,实验结果表明CDPSO算法具有绝对的优势,提出的方法和策略提升了算法的性能。在未来的工作中,将对CDPSO进一步改进,解决到约束MOPs和实际问题。