基于调谐质量阻尼器的风电机组振动抑制

王 磊，田 辉，孙鼎鼎，贺吉星，杨 波

（宁夏银星能源股份有限公司，银川 750021）

由于复杂风浪载荷和基础多自由度的特点，更容易产生超过风电机组结构极限的振动和变形，将在其关键部位产生严重的疲劳载荷，如叶根、塔根和塔架与机舱连接处[1]。这些缺点将影响风电机组的发电功率，严重时将会导致风电机组结构破坏和平台倾覆[2]。因此如何有效降低结构振动和弯曲程度成为设计时的关键问题[3]。

传统的结构抑制方式是通过不同工况下调节桨距角和转矩实现降低风电机组的结构载荷[4]。陈文婷等[5]在基于叶片根部载荷的PID 独立变桨的基础上，引入激光雷达并提出优化的独立变桨控制方法。但调节桨距角将使风轮减少受风面积，进而影响发电机转速，降低风电机组发电效率，因此寻求新的结构控制方法十分必要。

目前风电机组发展方向具有单机容量较大、塔式高耸结构的特点。调谐减振装置是在高耸结构中应用较广泛的控制装置，故将TMD 引入风电机组结构控制。Lackner 等[6]首次将TMD 应用于风电机组，研究了TMD 在机舱纵向布置下的结构减振效果，发现其对机组振动位移及载荷指标的减振率约为10%；Stewart[7]基于达朗贝尔原理建立了不同类型风电机组的3 自由度二维简化模型，采用遗传法优化了TMD 的刚度及阻尼；贺尔铭等[8]建立11 自由度的风电机组动力学模型，采用TMD-HMD 主被动综合控制方法，有效抑制风电机组振动；郑建才等[9]研究了垂荡板有效地降低风电机组系统的运动响应；陈建兵等[10]分析了风浪载荷作用风电机组结构的整体可靠性，建立了结合多体动力学理论与有限元方法的风电机组结构一体化耦合动力学分析模型。在上述研究中，有效抑制风电机组的结构载荷。但上述研究还存在下列问题：首先针对TMD 参数优化中，由于FAST 模型仿真周期较长，不能迅速寻得TMD 各参数的最佳配置；其次由于TMD 参数寻优区域具有强非线性，传统的寻优算法寻优能力有限，很可能陷入局部最优。

综上，本文针对风电机组机舱中配置的TMD 各参数进行寻优。首先依据风电机组结构特点，建立仿真计算更迅速、拟合更准确的含风浪载荷的动力学模型；其次采用辨识能力强的LM 算法分别寻得动力学模型中的结构未知参数和风浪载荷参数，并利用FAST 模型验证其准确性；再次利用寻优能力较强的蚁狮算法与含风浪载荷的动力学模型配合对TMD 参数寻其最优配置；最后利用FAST 全耦合模型验证寻优后的TMD对风电机组关键部位的载荷抑制能力。证明寻优后的TMD 在多种环境条件下均能显著提升风电机组的结构稳定性。

1 建立含风浪载荷的动力学模型

先前研究针对TMD 参数寻优需要多次调用FAST模型，因而需要大量仿真时间且存在大量无关计算；针对FAST 模型的仿真时间长、运算过程复杂等特点，本文基于风电机组关键模态建立的含风浪载荷的动力学模型，其仿真时间短、运算过程简单且能准确模拟风电机组关键部位的结构状态和疲劳载荷。

在风电机组研究设计中，美国可再生能源实验室开发的风电机组模型作为基础研究对象被广泛应用[11]，因此本文选用其作为研究对象。本文浮台选择为Barge型。风电机组的主要参数见表1。

表1 Barge 型风电机组的主要参数

1.1 建立含风浪载荷的动力学模型

以图1 中O 点为风电机组动力学模型旋转中心，塔架视为含有一阶纵弯的弹性体，浮台视为刚体，机舱TMD 视为质点，只考虑其水平运动自由度，浮台各个自由度锚链和水互相作用的阻尼和刚度等效为与浮台连接的弹簧和阻尼器。针对机舱空间尺寸限制，设置行程限制器。设置在距离TMD 初始位置±8 m 处接触。

图1 中m、I 表示质量和转动惯量，x、θ 表示偏离于Z 轴的位移和角度；k、d 为刚度和阻尼，R 为质心与参考点距离，下标t、p、T 表示塔架、浮台和TMD。

随着互联网技术的不断发展，中国已经进入到了“互联网+”时代，网络在各个行业中得以普及，给传统的发展带来了巨大的变革、机遇以及挑战。将企业财务管理创新与网络技术进行结合是当前财务管理方面发展的重要方向，本文结合“互联网＋”在企业财务管理中的影响与策略展开了探究。首先对企业财务管理理念进行分析，并对其进行改变，结合“互联网＋”的特点，积极对先进的企业财务管理平台进行引进，以达到提升综合工作效率的目的，减少人力方面的耗费，并通过创新的模式来通入其日常的工作，提升数据一体化程度。

图1 风电机组结构示意图

基于欧拉-拉格朗日（Lagrange）能量方程建立含风浪载荷的风电机组动力学模型。含有5 个广义坐标qi的Lagrange 方程可以表示为

式中：T 为系统总动能，J；V 为系统总势能，J；Qi为系统非有势力；L 为Lagrange 乘子；q˙i为坐标qi对应速度，m/s。

利用Lagrange 方程和小角度假设得到动力学模型的振动方程

式中：klim、clim为限制器阻尼系数和刚性系数，N/m、Nos/m；xlim为限制器设定位置，m；Mwind、Mwave为风和波浪等效载荷，N/m、Nos/m；fa为TMD 控制力，N。

1.2 TMD 控制力fa

因为白噪声拥有良好的数学特性，即功率谱密度SN（ω）为常数N0。

于是当白噪声信号输入到线性系统时，系统响应信号的功率密度谱SY（ω）完全由线性系统的频率特性H（ω）决定。

本文将低通白噪声信号输入动力学模型中作为TMD 控制力fa。在功率谱分析的角度更加清晰、准确地分析动力学模型振动模态。

含风浪载荷的动力学模型中一些参数可以在NREL 设计手册[12]中查找，例如浮台的质量mp、塔架的质量mt和各个位置质心到塔架底座的距离等；还存在一部分参数需要通过辨识得到具体数值，例如塔架及浮台的转动惯量、引入的2 个虚拟旋转阻尼结构参数及风浪载荷参数。本文将未知参数分为2 组辨识，分别为结构参数和风浪载荷参数。将辨识结果代入动力学模型，与FAST 模型对比仿真结果验证。

1.3 结构参数辨识及验证

需辨识的结构参数共6 个，向量表示为

式中：W 为权重矩阵；m 为输出参数的数量；n 为输出参数对应的数据长度；yj（ti）为ti时刻FAST 模型第j 个输出；fj（ti，U）为ti时刻动力学模型设为U 时的第j 个输出。

结构参数的辨识及验证流程如下：首先关闭TMD系统，令风浪载荷系数为0，打开塔架和浮台自由度；其次设置浮台初始俯仰角为8°，转子初始转速14 rpm，其他初始化参数为0；再次利用FAST 模型得到塔架前后位移、平台俯仰角的响应数据；最后利用LM 算法寻得动力学模型结构参数最佳数值。为了能快速准确地确认未知参数，需对未知参数进行初始猜测。如果初始值离最优值太远通常会导致收敛速度慢且结果令人不满意。动力学模型结构参数初始值和辨识结果见表2。

表2 动力学模型结构参数初始值和辨识结果

将fa分别输入动力学模型和FAST 模型，动力学模型和FAST 模型关键部位输出响应的频域和时域效果如图2 所示。从图2 中发现动力学模型和FAST 模型的输出响应拟合很好，在频域中3 个峰值分别出现在0.036 4、0.087 4 和0.540 4 Hz，分别与TMD、平台俯仰角和塔架弯矩的振动模态一致。

图2 输入fa 后动力学模型与FAST 模型对比图

1.4 风浪载荷参数辨识及验证

本文根据海风作用到塔架的力矩与风电机组转子的推力（RotThrust）成正比，通过RotThrust 乘以系数bwind等效为风载荷效果；在一定范围内波浪作用到浮台的力矩与浪高（WaveElev）成正相关，通过WaveElev乘以系数bwave等效为波浪载荷效果。其中RotThrust 和WaveElev 可从FAST 仿真结果得到。

在辨识中，本文将工况设置为平均风速12 m/s，有效浪高设置为4 m，此工况接近风电机组的额定工况。风浪载荷参数辨识过程如下：首先在FAST 模型仿真中得到RotThrust、WaveElev、塔架纵向位移和浮台俯仰角响应；其次将拟合后的结构参数代入动力学模型，将RotThrust、WaveElev 作为输出信号对bwind和bwave进行参数辨识。风浪载荷系数辨识结果见表3。

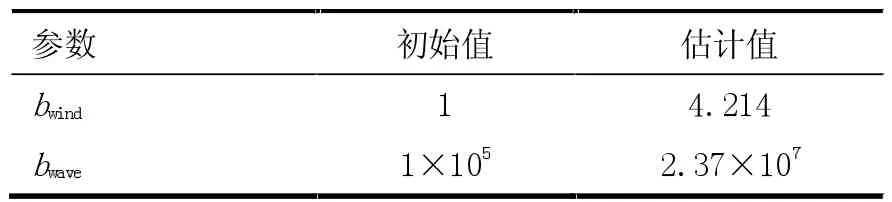
表3 动力学模型风浪载荷参数初始值和辨识结果

将辨识结果代入动力学模型，并与FAST 模型输出响应在频域和时域对比效果，如图3 所示。从时域和频域对比结果分析，虽然含风浪载荷的动力学模型与FAST模型输出响应在细节上存在一定偏差，这是由FAST 模型非线性的特点决定的，但动力学模型在频域中仍然能够较好地表现风电机组运行过程中的状态响应。

图3 含风浪载荷的动力学模型与FAST 模型对比图

2 蚁狮算法寻优

2.1 蚁狮算法和优化参数

蚁狮优化（Ant Lion Optimizer，ALO）算法是澳大利亚学者Seyedali Mirjalili 提出的一种新型元启发式群智能算法[13]。ALO 算法受蚁狮捕捉蚂蚁过程的启发，仿照蚁狮捕捉蚂蚁的过程来解决未知空间搜索实际问题。

在ALO 算法寻优过程中，蚂蚁和蚁狮的位置表示优化问题的解，蚁狮通过不断捕食蚂蚁寻找问题的最优解。因其良好的自适应边界收缩机制和精英主义优势，所以具有收敛速度快、全局搜索能力良好和需要调节的参数少的特点，与遗传算法和粒子群算法相比，ALO 算法只需选取合适的蚁狮数量和迭代次数即可进行优化，有效避免了参数设置不合理对优化过程和结果的影响，ALO 算法具有更好的优化效果。

由于风电机组结构的特点，漂浮式平台较多的自由度使风电机组在风浪影响下塔架纵向位移幅度明显增加，同时塔架纵向位移和塔基疲劳载荷关系密切[8]，因此本文将目标函数定义为塔架纵向位移标准差

式中：σt为有TMD 时塔架纵向位移标准差；σs为无TMD 时塔架纵向位移标准差；η 为塔架纵向位移标准差抑制率，%。根据工程经验，在寻优过程中mT约束在漂浮式风电机组的总质量的0.3%～1.8%[11]。

考虑机舱实际尺寸，TMD 的运动行程限制在一定区间内，其质量mT、刚度系数kT和阻尼系数dT的配置对减载效果起着决定性作用[14]，因此TMD 参数研究十分必要。根据前文建立的含风浪载荷的动力学模型设计目标函数，转化为求TMD 各参数最优值问题，利用寻优能力更强的蚁狮算法寻求TMD 各参数最优配置。

2.2 优化结果及分析

ALO 算法、粒子群算法和遗传算法设置参数见表4。由ALO 算法、粒子群算法和遗传算法寻得的TMD各参数最优解见表5。

表4 3 种智能算法设计参数

表5 TMD 各参数最优解

图4（a）、图4（b）为迭代稳定代数分布图、寻优结果分布图。对比多次寻优结果，ALO 算法拥有着更快的寻优速度和更稳定的寻优结果，而粒子群算法和遗传算法的寻优速度不稳定，且可能陷入局部最优解。

图4 迭代稳定代数和寻优结果分布图

图5（a）为无有TMD 的含风浪载荷的动力学模型塔架纵向位移对比图，如图可以发现优化参数后的TMD 大幅度降低了塔架纵向位移幅度，证明其有良好的减振效果。图5b 为TMD 的运动行程图，如图5（b）所示，TMD 的运动幅度在-9～9 m 之间，符合实际工程要求。

图5 TMD 参数优化后的减载效果

3 TMD 减载效果验证

3.1 设计工况

漂浮式风电机组结构振动响应载荷工况见表6，表中5 种工况为风电机组常见的环境工况。为充分发挥TMD 减载效果，将海浪谱峰频率设为11.8 s，这是平台和塔架的耦合频率。

表6 工况设计

3.2 减振效果分析

叶片和塔基作为风电机组中关键部位，本文重点分析风电机组塔基纵向载荷和叶片载荷，其中塔基纵向载荷通过塔基纵向剪力和纵向弯矩体现，叶片载荷通过叶根纵向弯矩和纵向剪力体现。图6 分别为在工况5 条件下，有无TMD 时塔架纵向位移和平台俯仰角的功率谱密度（PSD）和其时域对比图。图6（a）和图6（b）中发现载荷峰值集中在0.05～0.15 Hz，放置TMD 后显著降低在0.083 Hz 的最大峰值。图6（c）和图6（d）中发现在时域中放置TMD 后塔架纵向位移幅度和平台俯仰运动幅度降低20%。

图6 Barge 型漂浮式风电机组的PSD 比较

图7 是在5 种工况下TMD 对塔基纵向载荷和叶片载荷的抑制效果，从图7 中可以发现在不同工况下，TMD 的载荷抑制率均超过5%，最高达到了46%，证明TMD 能够有效抑制塔基纵向载荷和叶片载荷。

同时在图7 中发现TMD 在不同工况下，对关键部位载荷的抑制率呈V 型分布。相比于工况3 时，TMD在其他工况下表现出更好的减载效果。原因在于工况3 更接近风电机组的额定工况，在此工况下启动桨距控制，降低了风电机组关键部位载荷，进而证明TMD控制能与桨距控制配合，进一步降低风电机组关键部位载荷。

图7 TMD 对关键部位疲劳载荷标准差抑制效果图

4 结论

针对风电机组机舱中配置的TMD，利用蚁狮算法和含风浪载荷的动力学模型配合，寻求TMD 最佳配置，充分抑制风电机组关键部位载荷。本文主要结论如下。

1）根据风电机组的结构特点，依据欧拉-拉格朗日方程建立含风浪载荷的动力学模型，利用LM 算法分别对结构未知参数和风浪载荷系数辨识，并分别从时域和频域准确拟合FAST 模型。

2）利用蚁狮算法和含风浪载荷的动力学模型配合，对TMD 参数寻求最优配置，并与多种传统智能算法对比寻优结果，证明蚁狮算法能准确、快速地寻得TMD最优配置。

3）利用FAST 全耦合模型，从不同工况中分析TMD对风电机组关键部位载荷的抑制率，并证明TMD 在低于额定风速下和高于额定风速下载荷抑制效果更好，同时证明优化参数后的TMD 能有效抑制风电机组关键部位载荷，有效提升机组稳定性。