超大跨径钢管混凝土拱桥拱肋混凝土灌注过程调载分析
2023-03-17谢松李覃祚杰刘耀凤
谢松李 覃祚杰 刘耀凤
摘要:为改善超大跨径钢管混凝土拱桥混凝土灌注期间拱肋位移、线形及应力的影响,文章以平南三桥为工程背景,基于“位移最优,应力最佳”原则计算调载索力值,通过Midas Civil有限元软件建立拱肋模型,展开钢管混凝土灌注过程中拱肋位移、线形及应力分析。结果表明:混凝土灌注过程进行调载,可有效控制拱顶上挠值;拱肋轴线受混凝土灌注过程调载的影响较大,上游侧拱肋轴线偏差值减少40.12%,下游侧拱肋轴线偏差值减少46.67%;管内混凝土灌注过程不调载,管内混凝土的最大拉应力为1.85 MPa,灌注过程调载的管内混凝土最大拉应力为0.44 MPa,降低了76.22%,有效控制了管内混凝土的拉应力,避免混凝土发生拉裂破坏,保证结构受力合理及施工的安全。
关键词:钢管混凝土拱桥;拱肋;混凝土灌注;调载;变形;应力
0引言
钢管混凝土拱桥以其承载能力强、刚度大、适用性强等优势被广泛应用于深山峡谷等险峻地区。钢管混凝土灌注过程的优劣影响着钢管与混凝土协同工作的能力、结构施工的稳定性、拱桥承载力等。钢管混凝土灌注施工作为大跨径钢管混凝土拱桥的关键工艺之一,仍是目前国内外学者研究钢管混凝土施工的重点。王红伟等[1]基于稳定性理论,建立了主桁架结构的有限元模型,对大跨径钢管混凝土灌注过程中主拱肋的线形、应力和稳定性進行研究,结果表明:混凝土灌注过程中主拱肋跨中截面的偏位较大,结构稳定性逐渐降低。Zhao等[2]基于拱肋挠度影响线理论研究了控制拱肋挠度对结构使用寿命的影响。余强[3]以香火岩特大桥为依托,通过ANSYS软件建立拱肋计算模型,研究分析该桥管内混凝土灌注过程的拉应力变化状态,并基于拉应力变化状态提出调整方案。李长胜[4]以南盘江大桥和天峨龙滩特大桥为工程背景,基于实测数据建立有限元模型验证了扣索调载理论和扣索调载方案。关敬文等[5]通过有限元模型研究了钢管混凝土拱肋的应力变化及位移,当拱顶上挠达到60 mm时,需要对灌注过程进行调载以降低拱顶上挠量,但并未研究调载后对拱肋的影响。
平南三桥建成以后将超越波司登大桥成为世界上跨径最大的钢管混凝土拱桥。本文基于Midas Civil有限元软件,根据拱肋不同钢管施工阶段的划分,建立拱肋模型,研究该桥拱肋混凝土灌注过程中不调载和调载拱肋结构的位移、线形及应力变化状态,为其他超大跨径钢管混凝土拱桥拱肋混凝土灌注施工提供借鉴经验。
1 工程概况
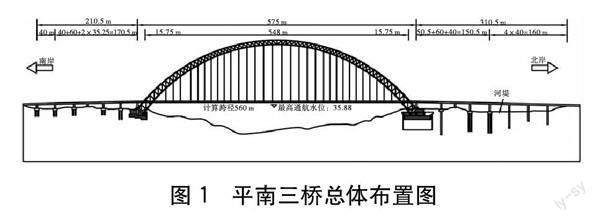
平南三桥是主跨为575 m的中承式钢管混凝土拱桥,计算跨径为560 m,矢跨比为1/4,拱轴线采用倒悬链线,悬链线系数为1.5。拱顶截面径向高为8.5 m,拱脚截面径向高为17.0 m,肋宽为4.2 m。每根拱肋上、下各安装两根1 400 mm的钢管混凝土弦管,管内混凝土采用C70。主拱肋通过横联钢管850 mm和竖向两根腹杆700 mm钢管连接主管而构成矩形截面,主管采用Q420qD钢材,总体布置如图1所示。拱脚下弦段为了提高防撞和防腐能力,外包C30钢纤维混凝土,钢纤维掺量为40 kg/m3。
2 施工阶段划分
拱肋混凝土采用C70高性能混凝土以泵压法自拱脚向拱顶灌注。如图2所示,灌注顺序为:上游内侧下弦管(1号管)→下游内侧下弦管(2号管)→下游内侧上弦管(3号管)→上游内侧上弦管(4号管)→上游外侧下弦管(5号管)→下游外侧下弦管(6号管)→下游外侧上弦管(7号管)→上游外侧上弦管(8号管)。单管分四级泵送;泵送过程采用抽真空辅助工艺。管内混凝土灌注过程中,在5段位置进行调载。
平南三桥钢管拱肋单侧半跨拱肋划分为11个节段,全桥共划分为44个吊装节段。为了便于有限元模型加载模拟,根据实际的灌注顺序将单根拱肋简化为9个两岸连续且对称的施工工况,全桥共计72个施工工况。模拟计算分两个方案进行,分别为不考虑混凝土灌注过程调载和考虑混凝土灌注过程调载,二者的施工工况划分相同,如表1所示。
3 数值模型的建立
3.1 材料参数、截面参数和单元类型
通过Midas Civil软件建立主桥主弦管模型,计算分析管内混凝土灌注过程对主弦管位移、线形及应力的影响。钢材自重按78.5 kN/m3计算,弹性模量为210 GPa,泊松比为0.3;C70高性能混凝土自重取25.49 kN/m3计算,弹性模量为37 GPa,泊松比为0.2。采用梁单元模拟拱肋;桁架单元模拟调载索。调载索是此次模拟的重点,通过改变调载索的施加力值影响拱肋的受力状态,进而对比不调载和调载后拱肋的位移、线形及应力状态。主要单元的类型、材料名称及截面形状尺寸如表2所示。
3.2 调载索参数
钢管混凝土灌注过程中,采用1 860 MPa,15.2 mm高强度低松弛钢绞线作为调载索材料,弹性模量E=1.95×108 kN/m2。调载索以P型锚具作为锚固端的截面形式,将其设置于拱肋5#节段端头附近的扣点位置。调载索布置如图3所示。
为简化计算模型,需对调载索的弹性模量进行换算以使得模型中的调载索伸长量与拱肋节点处的扣索伸长量一致。伸长量计算如式(1)所示:
Δl=FL/EA(1)
式中:F——索力(kN);
L——索长度(m);
E——索的弹性模量(MPa);
A——索的截面积(mm2)。
由式(1)可知,伸长量与索长度、索力、弹性模量和截面面积有关;当F和A确定后,索长度与弹性模量成正比,通过关系对模型中的扣索弹性模量进行换算。换算结果如表3所示。
本模型以“位移最优,应力最佳”为原则,采用影响矩阵方法计算调载索力值。调载索的调载力值Tt可通过式(2)~(4)确定[6]。
Tt=min(Ttmax)(2)
Ttmax=max(Tcmaxj)(j=1,…,9)(3)
Tcmaxj=(Scmaxj-St)/Ecj(4)
式中:Tt——理想调载索力(kN);
Ttmax——所用灌注方案的最大调载力(kN);
Tcmaxj——灌注第j根钢管的最大调载力(kN);
Scmaxj——第j根钢管在施工阶段所用灌注方案所引起的拱顶最大上挠量(mm);
St——拱顶目标上挠量(mm);
Ecj——灌注第j根钢管时,单位调载索力对拱顶的位移影响值。
每根主弦管混凝土灌注过程均采用上述调载方法进行调载,因此调载索力相同,具体数值如表4所示。
3.3 计算模型
根据材料参数、截面参数、单元类型及调载索力,并结合施工方案建立有限元模型,模拟分析混凝土灌注过程中的位移及应力变化。全桥有限元模型如图4所示。
4 结果分析
管内混凝土以泵压法自拱脚向拱顶顶升灌注,混凝土灌注过程进行不调载和调载模拟分析拱肋的位移、线形及应力变化情况。本桥两岸均为对称结构,因此混凝土灌注过程不调载及灌注过程调载仅提取南岸各测点数据进行分析。
4.1 位移分析
4.1.1 上游侧拱肋高程偏差分析
混凝土灌注过程不调载上游拱肋各控制点的高程偏差曲线见图5(a),在施工工况5下,管1、管3、管4及管9南上08~11拱肋段的高程偏差曲线与南上01~07拱肋段呈现反向增长趋势,其他拱肋段的高程偏差曲线变化趋势趋于稳定值,变化波动较小。其由于南上08~11拱肋段接近于拱顶,易受混凝土灌注狀态及自重影响所致。如图5(b)所示,混凝土灌注过程调载,上游拱肋各控制点的线形变化与混凝土灌注过程不调载拱肋各控制点的线形变化差距较小,且最大下挠值发生于南上11拱肋段,其值为481 mm,与混凝土灌注过程不调载拱肋的最大下挠值所发生的位置及数值相同。故由图5可知,灌注过程调载能有效减少拱肋的上挠值,因此混凝土灌注过程调载对上游侧高程偏差的下挠值影响不大,且在一定程度上可以减少拱肋上挠值。
4.1.2 下游侧拱肋高程偏差分析
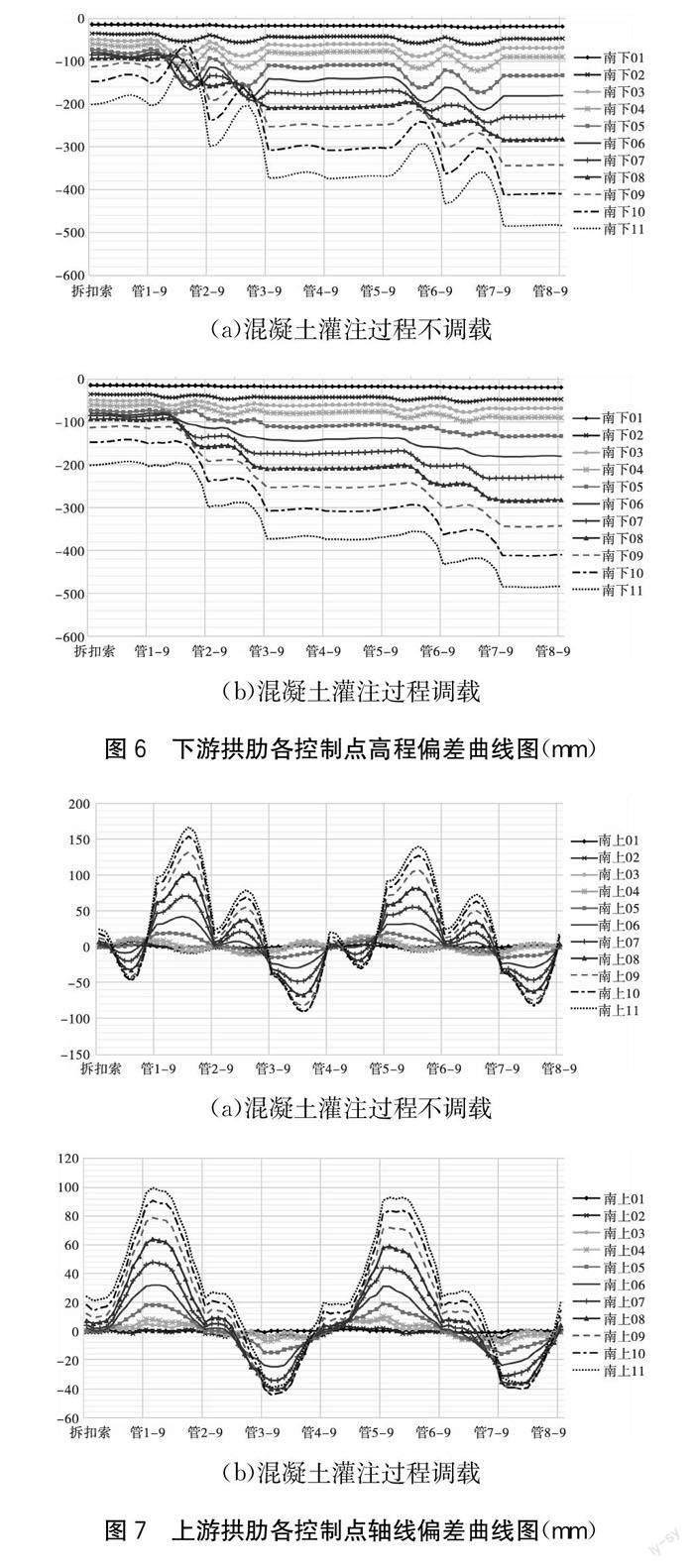
混凝土灌注过程不调载下游拱肋侧高程偏差曲线如下页图6(a)所示,与上游侧拱肋高程偏差曲线线形基本吻合;但其高程偏差波动点发生于管2、管3、管6和管7,与上游侧拱肋高程偏差曲线略有不同。究其原因,与钢管所处位置及水流方向有关,管1、管4、管5及管8位于上游侧。而混凝土灌注过程调载的下游侧拱肋高程偏差曲线与灌注过程不调载的拱肋高程偏差曲线突变点相吻合,且最高点及最低点基本一致,见下页图6(b)。
4.1.3 上游侧拱肋轴线偏差分析
如图7所示,混凝土灌注过程不调载和灌注调载的上游侧拱肋轴线偏差值均呈现循环性变化,从施工工况管1-1~管4-9为一个循环,此种现象由主弦管所处的位置所致。如下页图7(b)所示,每4根主弦管为一组,与桥轴线相对称。由于混凝土灌注过程中,拱轴线偏差只往一侧偏移,管1和管4的偏差值基本为负值;管2和管3的偏差值基本为正值,且灌注过程不调载的上游侧拱肋轴线偏差绝对值最大为167 mm;混凝土灌注过程调载的拱肋轴线偏差绝对值最大为100 mm,减少了40.12%,效果显著。
4.1.4 下游侧拱肋轴线偏差分析
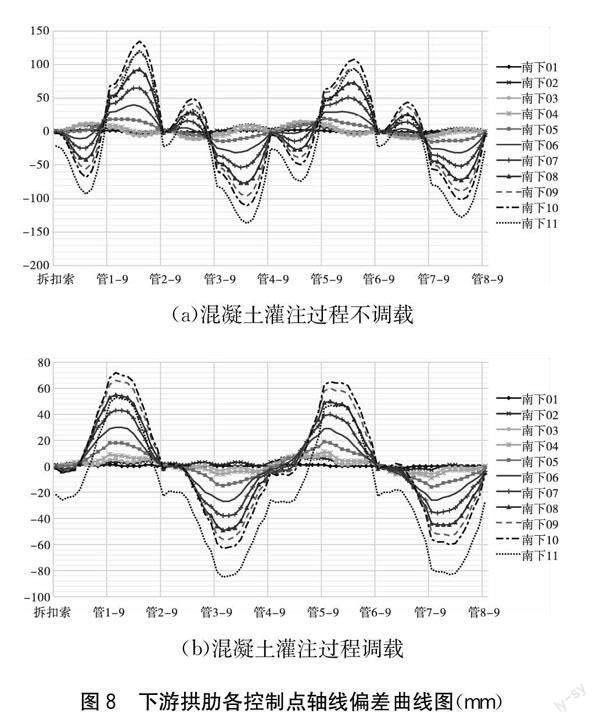
混凝土灌注过程不调载和灌注过程调载的下游侧拱肋轴线偏差曲线依旧呈现循环性变化的趋势。由图8可知,混凝土灌注过程调载的下游侧拱肋轴线偏差曲线变化更为显著,且变化范围有所增加。如图8(a)所示,混凝土灌注过程不调载的下游侧拱肋轴线偏差值变化范围为-137~135 mm,而图8(b)灌注过程调载的下游侧轴线偏差值变化范围则减少至-85~72 mm。负向绝对值降低37.96%;正向绝对值降低46.67%。由此可见,无论上游侧或是下游侧拱肋轴线偏差值在混凝土灌注过程调载后均有大幅降低,灌注过程调载可以在一定程度上减弱轴线的变位。
4.2 应力结果分析
拱脚、拱中和拱顶在不同工况下的应力曲线变化趋势相似,如图9~11所示。1号管和2号管位于拱肋下侧,主要承受压力,因此两根管之间会产生最大压应力,而3号管和4号管则主要承受拉应力。
混凝土灌注过程不进行调载,拱脚、拱中及拱顶的最大压应力均发生在1号管,分别为7.52 MPa、6.54 MPa及6.35 MPa;混凝土灌注过程调载后1号管拱脚、拱中、拱顶最大压应力分别为6.49 MPa、6.74 MPa及5.37 MPa。由此可知,混凝土灌注过程调载基本不对拱中压应力产生影响,但可降低13.70%和17.76%的拱脚和拱顶压应力。而混凝土灌注过程不调载的管内混凝土最大拉应力发生在3号管拱脚处,为1.85 MPa;灌注过程调载后则降低为0.44 MPa,降低了76.22%。显然,混凝土灌注过程调载可大幅降低管内混凝土拉应力,满足规范要求[7],且利于施工。
5 结语
(1)混凝土灌注过程进行调载,上下游的高程偏差变化差异较小,能有效控制拱顶上挠值,但对拱肋的最终下挠值基本无影响。
(2)拱肋轴线受混凝土灌注过程调载的影响较大,上游侧拱肋轴线偏差值减少40.12%,下游侧拱肋轴线偏差值减少46.67%,但拱肋的轴线线形无论是混凝土灌注过程不调载或是灌注过程调载均呈现循环性变化。
(3)管内混凝土灌注过程不调载,管内混凝土的最大拉应力为1.85 MPa;混凝土灌注过程调载的管内混凝土最大拉应力为0.44 MPa,降低了76.22%,有效地控制了管内混凝土的拉应力,可避免混凝土发生拉裂破坏。
参考文献:
[1]王红伟,谢开仲,郭 晓,等.大跨度钢管混凝土拱桥拱肋混凝土灌注过程稳定性研究[J].世界桥梁,2019,47(5):49-53.
[2]ZHAO Zhan,NIE Zhenhua,MA Hongwei.Damage identification of the arch bridge based on the difference of deflection with moving load[J].Applied Mechanics & Materials,2014,578(7):1 096.
[3]余 强,钢管混凝土拱桥拱肋安装与管内混凝土灌注应力调整研究[D].重庆:重庆交通大学,2017.
[4]李长胜.钢管混凝土劲性骨架拱桥外包混凝土浇注过程扣索调载研究[D].南宁:广西大学,2021.
[5]关敬文,王楚杰.中承式钢管混凝土拱桥拱肋管内混凝土灌注过程分析[J].西部交通科技,2018(10):124-129.
[6]潘 栋,邓年春,涂 兵,等.基于智能主动调载技术的超大跨CFST拱桥灌注顺序分析[J].公路,2020,65(9):130-137.
[7]TB10092-2017,铁路桥涵混凝土结构设计规范[S].
作者简介:谢松李(1984—),工程师,主要从事道桥工程施工及技术管理工作。
