基于人工蜂群算法的毫米波大规模MIMO 混合预编码设计

肖 晴, 谭方青∗, 徐 超

(1.桂林电子科技大学 广西无线宽带通信与信号处理重点实验室,广西 桂林 541004;2.桂林电子科技大学 信息与通信学院,广西 桂林 541004;3.中国电子科技集团公司第五十四研究所,河北 石家庄 050081)

0 引言

毫米波大规模多输入多输出(Multi-Input Multi-Output,MIMO)技术因其具有高带宽、大吞吐量和高能效等优点受到国内外学者广泛关注,成为当前通信领域研究的关键技术[1-2]。 毫米波的短波长特点使其能够在相同的面积上部署更多的天线,而大型天线阵列产生的增益足以补足毫米波的传输损耗[3]。 同时,毫米波的窄波束特性可以使信号更精确地指向接收端下行用户,进一步提高在该方向的传播距离和数据速率。

全数字预编码技术可以灵活调整信号的幅度和相位,但要求天线阵列中每个阵元都配备专用的射频(Radio Frequency,RF) 链路,在最大化大规模MIMO 系统的频谱效率的同时也产生了巨大的硬件成本和能耗[4]。 传统的模拟预编码技术成本较低,但只能传输单数据流,系统性能较差[5]。 为了降低硬件成本且提高系统性能,下行链路混合预编码技术成为了关注热点[6-8]。 根据RF 与天线的映射方式的不同,目前混合预编码系统主要有2 种结构[9]:一种是全连接结构[10-12],每根天线都与所有的RF相连,充分利用了天线增益,但系统硬件开销很大;另一种是部分连接结构[13-15],RF 仅需与固定的天线数相连,大幅减少了移相器等硬件的使用,系统能量效率更高,更具有实用性。 然而,在现有的技术中,模拟预编码矩阵往往受限于移相器网络的恒模约束,使得设计问题转变成了NP-hard 问题。 为了降低问题的设计难度,针对部分连接结构,文献[16]利用连续干扰消除的思想来设计混合预编码,该方案利用功率迭代算法使得运算复杂度降低,但是射频信号会受限于幅度的限制。 文献[17-18]提出基于粒子群优化(Particle Swarm Optimization,PSO)的混合预编码方案,该方案运算复杂性较低,且没有用户数等于RF 数的限制,但是算法本身的收敛性能较差。

在此背景下,针对部分连接结构,提出一种基于人工蜂群(Artificial Bee Colony,ABC)算法的混合预编码新算法。 具体地,第1 阶段,采用迫零(Zero-Force,ZF)预编码作为数字预编码,并将信道矩阵与模拟预编码矩阵的乘积构建为等效信道;第2 阶段,根据最大系统和速率准则设计模拟预编码矩阵,并据此建立待优化的目标函数,使用ABC 算法对此目标函数进行寻优,进而求得最优的预编码矩阵。 针对基本的ABC 算法存在探索与开发能力难以达到很好平衡的缺点,又提出一种改进的ABC 算法,即交叉操作的全局人工蜂群(Crossover Global Artificial Bee Colony,CGABC)算法。 经过计算机仿真,验证了改进算法的有效性。

1 数据传输模型

考虑下行链路多用户毫米波大规模MIMO 系统,如图1 所示。 假设已通过信道互易性获得矩阵H 。 基站端发送Ns路数据流通过数字预编码器,即,其中,,n=1,2,…,Ns进行数字预编码,每一路数据流通过相应的RF 后,再由M个移相器组成的模拟预编码器对其进行模拟预编码,其中模拟权重矢量可表示为fn∈CN×1。 系统总发射天线数Nt=MN,接收端为单天线,用户数为K。

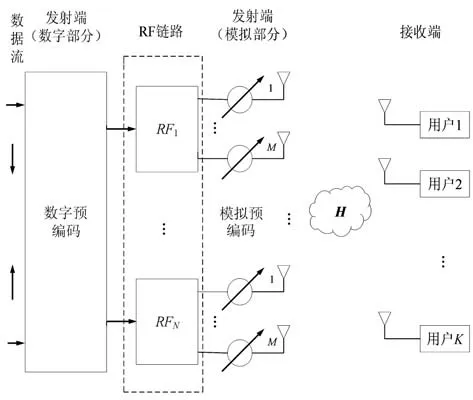
图1 部分连接的毫米波大规模MIMO 系统模型Fig.1 Partially connected millimeter wave massive MIMO system model

1.1 系统模型

此系统中,所有用户端的接收信号y ∈CK×1可以表示为:

式中,H =[h1h2… hK]T∈CK×MN,表示信道矩阵;FRF表示模拟预编码矩阵,具体可表示为:

式中,fi∈CM×1,i = 1,2,…,N中的元素可表示为,l=1,2,…,M。 由此可见,FRF随移相器相位θ =[θ1,θ2,…,θNt]的变化而变化,其中,θj=θi+(l-1)N=θil,j=1,2,…,Nt,i=1,2,…,N,l=1,2,…,M为第j个移相器的相位。 FBB表示数字预编码矩阵,s ∈CNs×1为 发 送 信 号,满 足INs,INs表示Ns×Ns的单位矩阵,n ∈CK×1表示加性高斯白噪声,即n ~CN(0,σ2IK),σ2表示方差。FRF和FBB满足总发射功率约束条件,即‖FRFFBB‖2F=Ns。 基于此,第k个用户的信干噪比(SINR)可表示为:

因此,系统中用户的和速率可表示为:

1.2 信道模型

由于毫米波的有限的空间散射特征[19],本文采用Saleh-Valenzuela 信道模型[20-21],其信道转移矩阵可表示为:

式中,λ表示载波波长;d表示天线间的距离。

2 基于ABC 算法的混合预编码方案

2.1 模拟预编码设计准则

大规模MIMO 系统中,ZF 预编码可以应用于数字域消除用户间的干扰,且复杂性较小,因此,本文数字域部分采用ZF 预编码设计。 基带预编码矩阵可设计为,式中,He=HFRF表示等效信道矩阵,c表示归一化因子,它的引入能够保证发射功率恒定不变, 且c满足。 基于图1 所示的大规模MIMO系统模型,为使系统总速率最大,则应对模拟预编码矩阵进行优化设计。 该设计问题中,FRF应满足的条件,如定理1。

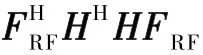
证明:将代入到式(1)中,可得接收信号为:

由式(3)、式(4)和式(8)可得出第k个用户的可达速率为:

每个用户的可达速率都可表达为式(9)的形式,所以使系统可达和速率最大,等价于让c2最大。 又由于:

因此,本文的优化目标函数可建模为:

2.2 基于ABC 算法的解决方法

ABC 算法是2005 年由土耳其学者Karaboga 发明的一种群智能进化算法,它在求解NP 类问题上具有优异的性能[22],因此考虑采用ABC 算法来优化此问题。

在传统的ABC 算法中,蜂群被划分为引领蜂、跟随蜂和侦察蜂3 类。 每个蜜源对应一个引领蜂,而且每个蜜源的位置都代表一个调度方案。 其迭代优化过程如下:

输入:NP为初始的θ 方案数;Niter为最大迭代次数;H 为信道矩阵;Nt为向量θ 的维度;K为接收天线数。

步骤3:引领蜂搜索。

在当前第t代引领蜂种群中,随机选择个体r1∈{1,2,…,NP/2}与目标个体θti按式(13)进行交叉搜索,从而产生新个体。

步骤4:跟随蜂搜索。

步骤5:侦察蜂搜索。

将2 种新形成的蜂群结合,判断其中是否发生了侦察蜂行为,即一个个体在连续进行Limit 次迭代后,仍未发生改变。 若发生,则按式(13)进行侦察蜂搜索产生新个体,并按式(14)选择适应度值较优的个体进入迭代种群。

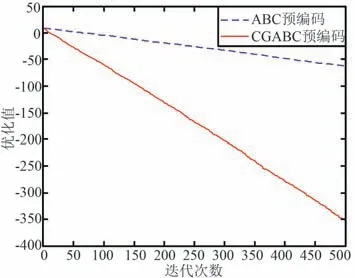
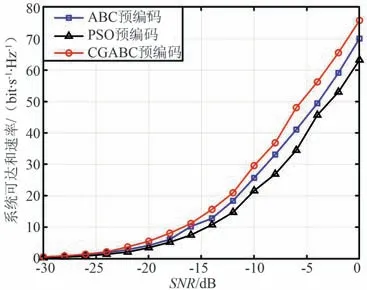
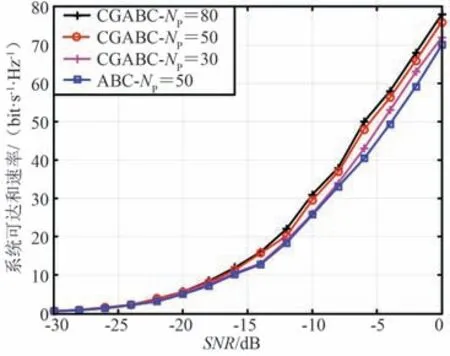
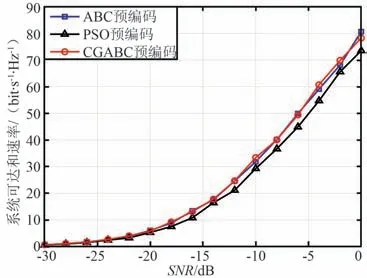
步骤6:根据适应度值评估NP个即得函数值,保留表现更好的θ 向量,记录为θelite。 当t

步骤7:令t=t+1,当t

步骤8:当t=Niter时,以θelite生成模拟预编码矩阵,即,i=1,2,…,N,l=1,2,…,M,FRF=diag{f1,f2,…,fN},将其带入式(4)得到系统可达和速率R。

输出:FRF,R。

3 基于改进ABC 算法的混合预编码方案

在高维非线性问题中,基本ABC 算法在迭代后期易陷入局部最优值,并且存在探索与开发能力之间的平衡矛盾问题。 因此,本文在基本ABC 算法的架构上,为进一步提高算法的寻优性能,减少陷入局部最优解的可能性,提出一种改进的ABC 算法用于模型求解。

3.1 引领蜂搜索过程的改进

对于2.2 节的引领蜂搜索过程,目标个体寻优搜索的维度比较单一,缺乏对全局的探索,因此易陷入局部最优值。 对此,引入二项交叉机制(如式(16)所示)和全局精英策略,从而提高全局开发和探索能力,如式(17)所示。

式中,cr~U(0,1),称为交叉因子,经多次实验,在改进的ABC 算法中,cr 为0.5 时能在开发与探索能力之间取得较好的平衡。

3.2 跟随蜂搜索过程的改进

对于2.2 节的跟随蜂搜索过程,其本质是以较大的概率对优良蜜源进行进一步搜索。 因此,引入自由搜索算法中灵敏度的概念,将其与蜜蜂的信息素相配合进行区域选择蜜源。 其中,跟随蜂的灵敏度是随机的,满足S(i)~U(0,1),蜜源的信息素nξ(i)可表示为:

找出满足nξ(i)≤S(i)条件的蜜源。 这种搜索蜜源的方法使蜜源选择更具有方向性,而且对算法的收敛性能也不会有太大的影响。

基于此,改进后的方案流程如图2 所示。

图2 改进ABC 算法流程Fig.2 Improved ABC algorithm flowchart

4 仿真分析

基于 Matlab 仿真环境, 验证提出的 ABC,CGABC 算法性能,并与现有的PSO 算法[17-18]进行对比。 实验基于图1 所示的下行链路系统模型,参数设置如表1 所示。

表1 仿真参数Tab.1 Simulation parameters

图3 和图4 分别为最大迭代次数为500 时在输入为Sphere 测试函数的情况下,ABC 和CGABC 算法的最优适应度值和收敛曲线的对比图。 从图3 和图4 中可以看出,相较于传统的ABC 算法,CGABC算法有更优的性能及更快的收敛速度,表明了算法在探索与开发能力之间达到了很好的平衡,从而验证了所提CGABC 算法的有效性。

图3 ABC 和CGABC 算法的优化值对比Fig.3 Comparison of optimal values of ABC and CGABC algorithm

图4 ABC 和CGABC 算法的收敛情况对比Fig.4 Comparison of convergence of ABC and CGABC algorithm

图5 给出了当Nt=64,NRF=K=16,采用ZF 数字预编码时,低信噪比(SNR)情况下,不同混合预编码方案的系统可达和速率随SNR 变化的情况。 由图5 可以看出,随SNR 的增大,基于CGABC 算法的方案系统性能最优,基于ABC 算法的方案次之,均优于基于PSO 算法的方案。 这是因为CGABC 算法中引入的与全局最优值的交叉机制在提高算法开发能力的基础上,也增加了算法的搜索能力,提升了算法的收敛速率。

图5 不同预编码方案下的系统可达和速率随SNR 变化的对比 (Nt=64)Fig.5 Comparison of achievable sum rates with SNR under different precoding schemes (Nt=64)

图6 给出了初始种群数目NP的变化对基于改进算法的方案的系统性能的影响。 从图6 可以看出,基于CGABC 算法的方案性能总是优于基于ABC 算法的方案性能,其中NP=80 时,基于CGABC算法的方案性能最优。 这是因为在空间维度一定的情况下,随着种群数目的增多,算法的收敛精度会得到一定程度的提高。

图6 NP 数目不同时,不同预编码方案系统性能对比Fig.6 System performance comparison of different precoding schemes when the number of NP is different

图7 给出了当Nt=128,NRF=K=16 时,低SNR情况下,不同混合预编码方案的系统总可达速率随着SNR 增大而增高的曲线图。 由图7 可以看出,当增大发射天线的数目为用户数的8 倍时,相比图5,虽各方案的系统性能都有一定程度的提升,但图7中,基于CGABC 算法方案的性能并不总是优于基于ABC 算法方案,这是因为进行交叉操作的概率系数可能不总是同样适用天线数目大幅增加的情况。可见,变量维度的大幅增加会对CGABC 算法的性能优势造成一定的影响。

图7 不同预编码方案下的系统可达和速率随SNR 变化的对比(Nt=128)Fig.7 Comparison of achievable sum rates with SNR under different precoding schemes (Nt=128)

5 结束语

针对传统的毫米波大规模MIMO 系统硬件成本高及计算复杂度大等问题,本文提出采用ABC 算法来设计混合预编码。 首先,以系统总速率最大为准则设计混合预编码矩阵,推算了预编码矩阵的优化问题可以等效为对模拟移相器相位的寻优设计,但这是一个NP-hard 问题;然后,针对这一复杂度高的非线性问题,采用ABC 算法进行优化求解以得到最优的预编码矩阵;最后,针对基本的ABC 算法探索与开发能力之间存在平衡矛盾的问题,又进一步提出基于CGABC 算法的混合预编码方案,改进了基本ABC 算法的性能缺陷。 仿真结果表明,本文所提出的混合预编码算法实现了较好的系统性能,基于CGABC 算法的解决方案性能更优,且具有一定的实用性。