基于因子分析法的粗集料形态特征综合评价

2023-03-16王惠敏汪海年孔庆鑫赵云飞雷鸣宇冯珀楠

材料科学与工程学报 2023年6期

王惠敏,汪海年,孔庆鑫,赵云飞,雷鸣宇,冯珀楠

(1.长安大学公路学院, 陕西西安 710064; 2.杭州交投建管建设集团有限公司, 浙江杭州 310024)

1 前言

沥青混合料中集料的性质对沥青路面的工程质量有着十分重要的影响,尤其是粗集料的形态特征[1-2]。粗集料的形态特征包括轮廓形状、棱角性和表面纹理,与沥青混合料空间骨架的形成以及沥青与集料之间的相互作用密切相关,显著地影响着沥青混合料的路用性能[3]。传统的试验评价方法无法直接有效地表征粗集料的形态特征,而且利用数字图形处理技术得到的指标较为单一,无法充分反映粗集料各类形态特征的细节差异[4]。因此,近年来集料形态的综合评价逐渐成为研究热点。

为了准确评价粗集料的形态特征,国内外学者先后采用图像处理和算法优化等方式进行了深入研究。侯云飞等[5]考虑到三维(3D)图像中存在的复杂情景,进行了优化处理,利用微分法实现了粗集料颗粒体积的测量,利用球当量径算法对粗集料颗粒粒径进行判定,并与人工试验进行对比,证明了粗集料体积和粒径判定的可行性。龚芳媛等[6]利用数字图像处理技术进行粗集料颗粒的数字化分类,利用傅里叶函数的集料模型与原始集料进行对比,对不同形状和棱角的粗集料进行分类。杨皓丹等[7]采用Image-Pro Plus软件和高精度电感传感器对集料进行研究,并引入3D特征指标参数厚宽比ξ,对集料3D形态指标进行量化描述。Janardhana Reddy[8]提出一种新的3D形状指标表面积比,通过测试集料的表面积和体积,确定集料的表面积比。上述方法可以实现对不同形状粗集料进行合理分类,避免测试的主观性和偏差,但指标涉及的各类设备及方法操作难度较大,且依赖于各种设备及模型,不利于现场实际操作。

综上所述,本研究利用形态学图像处理和边缘追踪算法获取粗集料的外部轮廓,在此基础上,利用因子分析法对常见且操作相对简便的粗集料形态特征指标进行分析处理,从而获得粗集料的综合评价指标。最后利用相关研究中认可度较高的集料形态评价设备和方法对提出的指标进行合理性验证。

2 基于Canny算子的粗集料指标采集与结果分析

2.1 粗集料颗粒图像采集

为了对粗集料的形状和棱角性两个方面进行评价,从3D层面反映出粗集料的形状特征和棱角特征,沿粗集料的结构最大断面面积方向进行2D断层切片图像提取。图像边缘是图像属性区域和另一属性区域的交界处,是区域几何特征发生突变的位置,也是图像中不确定性最大、信息最集中的位置。此外,边缘轮廓是易影响集料图像识别准确性的形态信息。因此,采用边缘检测方法对图像的边缘进行处理,其中最为重要的即为充分抑制噪声并保证图像边缘的连续性。现有的边缘检测算子有Robert算子、Sobel算子、拉普拉斯算子、Prewitt算子、Krisch算子、Log算子和Canny算子等[9]。相较于其他算子,Canny算子边缘检测具有较好的连续性,同时图像处理的清晰度也较高[10]。因此利用Canny算子的边缘检测依次提取多个二维截面图像,对边缘点进行追踪识别,获取边界对应点周围的8邻域,借此判断是否为边缘点,最终获取粗集料二维边缘图像,上述步骤均基于MATLAB代码编写实现。不同算子处理的图像如图1所示。

图1 不同算子的图像处理结果

采用Canny算子的集料图像边缘检测技术,主要基于信噪比准则、定位精度准则和单边响度标准提出。为求得边缘点,首先要通过高斯滤波器与原图像卷积得到平滑图像[11-12],计算公式如下：

(1)

G(x,y)=H(x,y,σ)*f(x,y)

(2)

式中：σ为高斯滤波器的标准差。

再通过一阶偏导、非极大值抑制和双阀值算法等实现集料的边缘检测[13-14]。

利用边界追踪算法区分强边缘点和弱边缘点,利用边界追踪检验强边缘点的真实性。通过假定一个边界或者二值区域R,进一步说明边界追踪算法的操作步骤,如图2所示[15]：

图2 边界追踪算法说明(算法找到的点标为灰色方块)

(1)随机选取一个强边缘点在左上角记为b0。c0与b0相邻。将c0绕着b0进行旋转,对b0的8个方向上的邻点依次识别;(2)令b=b1和c=c1;(3)从c开始顺时针方向出发,记b的8个方向上的邻点为n1,n2…,n8。找到标为1的第一个nk;(4)令b=nk和c=nk-1;5)重复步骤3和步骤4,直到b=b0且找到的下一个边界点为b1。

对强边缘点以及可能是边界的弱边缘点按顺时针方向跟踪形成目标边界,并顺次连接,形成闭合目标,最终获得目标边界图像。

2.2 粗集料颗粒图像处理结果

采用自行研制的设备—基于3D点云的集料形态检测系统,对粗集料进行颗粒图像获取。该设备利用线激光对待测集料进行扫描,可获取集料不同水平切面的二维图像。图3为一个颗集料二维图像的边界处理过程。

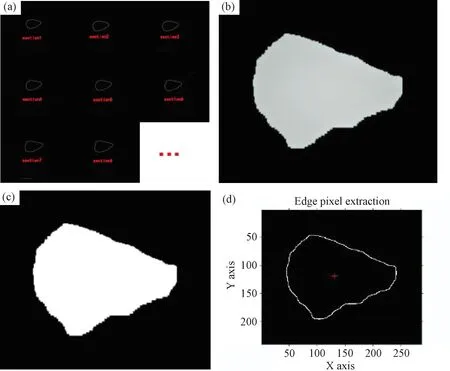
图3 单颗集料切面边缘提取结果 (a)原始集料切面图像;(b)Canny算子提取的边缘; (c)双阈值检测去除噪声;(d)边界追踪

由图3可知,通过Canny算子和边界追踪算法可以更好地反应集料二维图像边缘的变化特征,不仅抗噪性能强,其定位精度也很高,可以很快的识别出图像边缘的梯度周长,图像边界闭合的面积等信息,以便根据边缘特征提出准确合理的集料形状和棱角评价指标。

3 基于因子分析法的粗集料形态特征指标建立

3.1 粗集料形态特征评价指标初选

随着数字图像处理技术的不断发展,相关研究已逐步提出了多种集料形态评价指标[16]。评价指标主要分为基于3D图像和2D图像的方法,根据基本几何形态评价方法,以指标的算法简洁易操作和认可度为主要依据,进而选取合适的指标进行研究,从而将各基本指标组合形成多个量化指标相结合的综合表征指标,选取的指标如表1所示[17-26]。

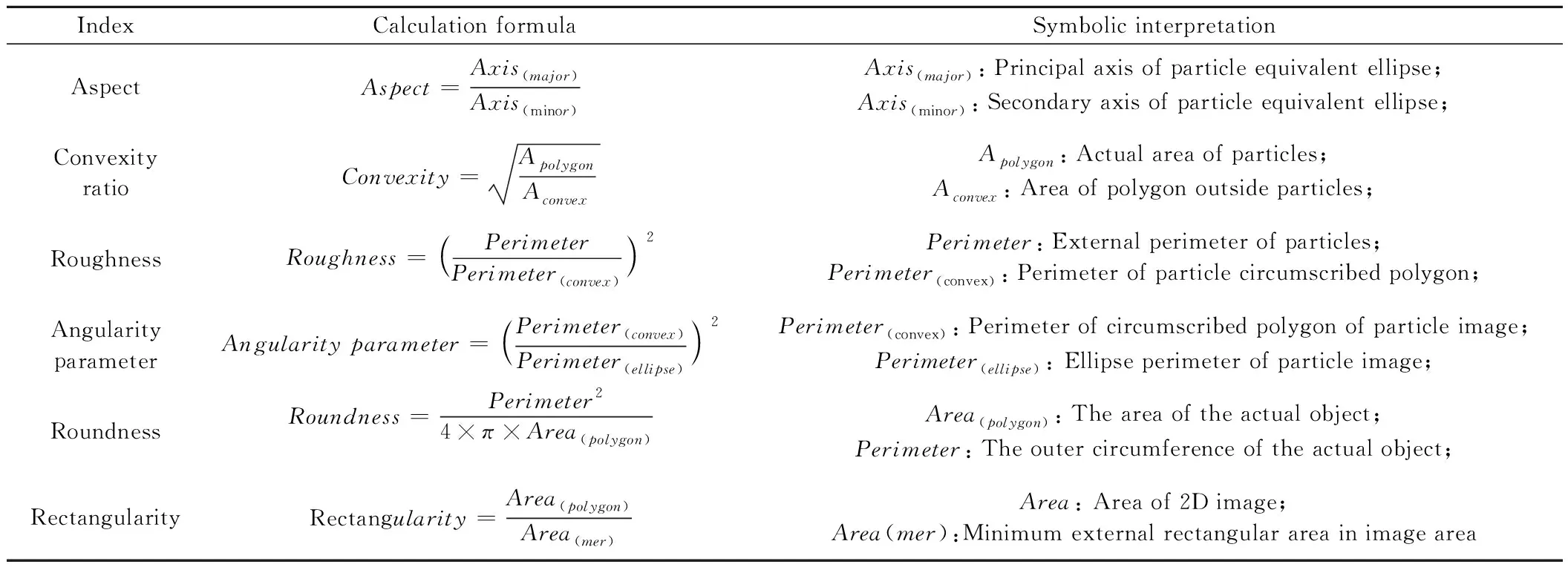
表1 集料评价指标

3.2 因子分析法

通过对上述六个指标进行具体的数据分析,找到其中主要影响粗集料形状和棱角特征的指标,选用其中几个指标开展集料相关性的描述,试验的因子分析法主要分为以下几个步骤：

3.2.1检验变量相关性利用KMO(kaiser-meyer-olkin)和巴特利特检验粗集料指标变量之间的相关性。当KMO>0.6时,表明变量间的相关性较好,结果如表2所示,KMO值为0.883>0.6,说明该测试指标数据适用于进行因子分析。

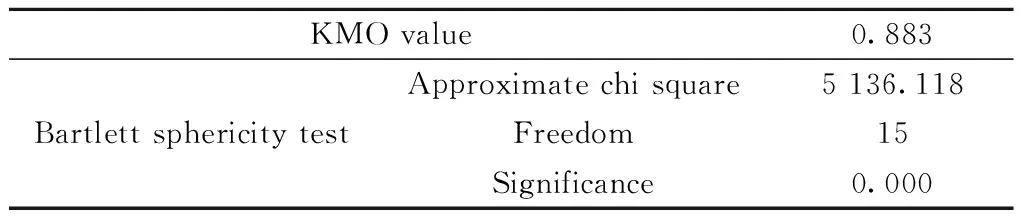
表2 KMO和巴特利特检验

3.2.2数据处理为了更好的得到集料的形状和棱角评价的综合指标,并消除摆放面对激光线在选取集料水平切面的影响,选取集料的两次不同摆放方向的图像。本次试验选取每种岩性每档粒径各200颗,共计1 800颗,对1 800颗集料二维图像进行分析,部分不同粗集料颗粒的指标值如表3所示。

表3 不同粗集料颗粒指标测试值

对抽取的样本进行正态分布规律分析,绘制概率密度分布图,根据样本偏度SK、样本峰度KU,对各个指标的正态分布情况进行检测,对不符合正态分布进行样本修正。

对测试指标选取显著水平a=0.01,P=0.99,根据样本数1 800,查得偏度检验和峰度检验的临界值如表4所示。

表4 偏度检验和峰度检验的临界值

根据样本偏度SK、样本峰度KU判断各个集料形态测试指标的正态性,分别对轴向系数、凸度、粗糙度、棱角参数、圆度、矩形度这六个指标进行由小到大排列,绘制六个指标概率密度分布图,如图4所示。

图4 不同指标概率密度分布图 (a)轴向系数;(b)凸度;(c)粗糙度;(d)棱角参数;(e)圆度;(f)矩形度

由图4可知,通过偏度检验,轴向系数和矩形度符合正态分布(偏度=0),凸度、粗糙度、棱角参数呈现左偏分布,圆度呈现右偏分布;通过峰度检验,轴向系数符合正态分布,棱角参数呈现瘦尾(峰度值<3),圆度、粗糙度、凸度、矩形度呈厚尾(峰度值>3)。根据偏度和峰度对六个指标样本数据进行修正,保证所有指标符合完全正态分布,对数据进行新的调整和赋值。

为消除指标间的差异,将赋值后的数据进行正向化处理,将逆向指标转化为正向指标。处理后的数据结果如表5所示。

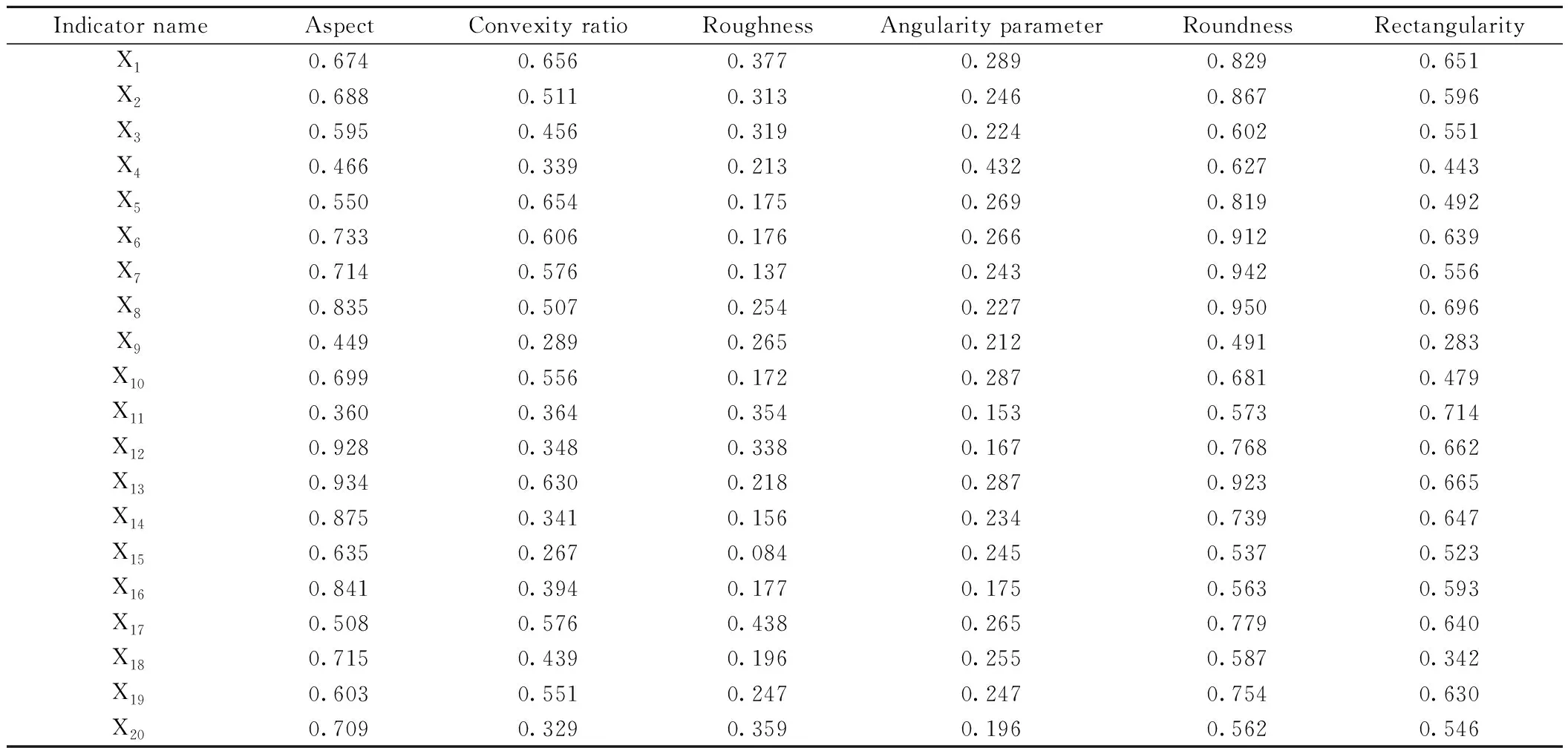
表5 不同粗集料颗粒指标测试值

3.2.3综合得分系数为探究不同粗集料粒径和岩性对指标的影响,针对不同产地的石灰岩、玄武岩和辉绿岩分别计算不同指标的综合得分模型系数,两种计算结果如图5所示。

图5 不同粒径(a)和不同岩性(b)集料的综合得分系数

从图5可知,不同集料粒径指标的得分系数基本保持不变,矩形度和轴向系数随着集料粒径的增大,综合得分系数不断增大;凸度、棱角参数随着粒径的增大,综合得分系数不断减小,这可能是由于各个指标评价效果受到集料粒径变化的影响,集料的粒径越大,形状对综合得分系数的影响程度越大;不同岩性集料的综合得分模型系数没有明显的变化趋势,可得岩性对集料形态指标基本没有影响。

3.2.4结果调整对研究的六个指标数据进行旋转后因子的载荷系数和因子的共同度计算,再进行浓缩因子处理,旋转后因子载荷系数见表6。

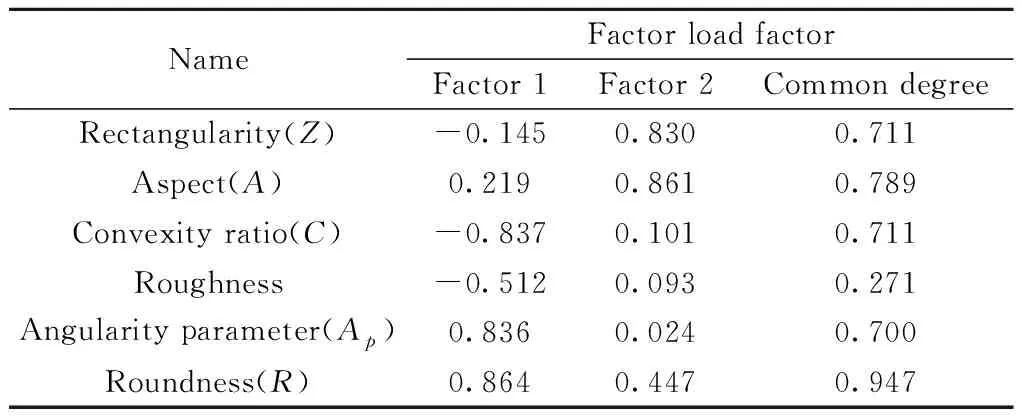
表6 旋转后因子载荷系数表

通过判断共同度是否大于0.4,可明确该指标是否可评价该研究内容,由表6可知,矩形度、轴向系数、凸度、棱角参数、圆度的共同度都大于0.4,故可用于评价粗集料的形态特征。根据旋转后的因子载荷系数,得到两个因子,因子1主要是由凸度、棱角参数和圆度决定,因子2主要是由轴向系数、矩形度、圆度决定。

将矩形度、轴向系数、圆度分为一组,将凸度、圆度、棱角参数分为另一组,分别进行数据研究,可以得到关于粗集料形状因子2和粗集料棱角因子1的旋转因子载荷系数,并得到共同度,旋转后因子载荷系数见表7和表8。

表7 旋转后形状因子载荷系数表

表8 旋转后棱角因子载荷系数表

3.3 粗集料形态综合指标建立

通过结果调整,可以得到因子得分关系式如式(3)所示：

f1=β11x1+β12x2+…+β1pxp

f2=β21x1+β22x2+…+β2pxp

… …

f3=β31x1+β32x2+…+β3pxp

(3)

根据上述各个指标的因子载荷系数,将上述标准化的数据计算公式代入因子载荷系数,得到关于粗集料形状特征和棱角特征的两个因子得分表达式,如式(4)所示：

ASI=0.662Z+0.892A+0.784R

AEAI=0.832C+0.925R+0.839Ap

(4)

式中：Z为矩形度、A为轴向系数、R为圆度、C为凸度、R为圆度、Ap为棱角参数、ASI(aggregate shape index)为形状因子、AEAI(aggregate edges and angularity index)为棱角因子。

利用SPSS对所有数据进行逆标准化处理,得到粗集料形态综合表达式,如式(5)和(6)所示：

粗集料综合形状指标 (ASI)为：

ASI=6.504 2-0.828 5Z-1.032 4A-2.214 7R

(5)

粗集料综合棱角指标 (AEAI)为：

AEAI=11.582 0+1.705 0C-2.613 2R-

8.225 5Ap

(6)

3.4 结果分析

根据粗集料综合形状指标和综合棱角指标表达式,对1 800颗集料的指标值进行计算并排序,得到ASI和AEAI的最大值和最小值,部分指标值的计算结果见表9。

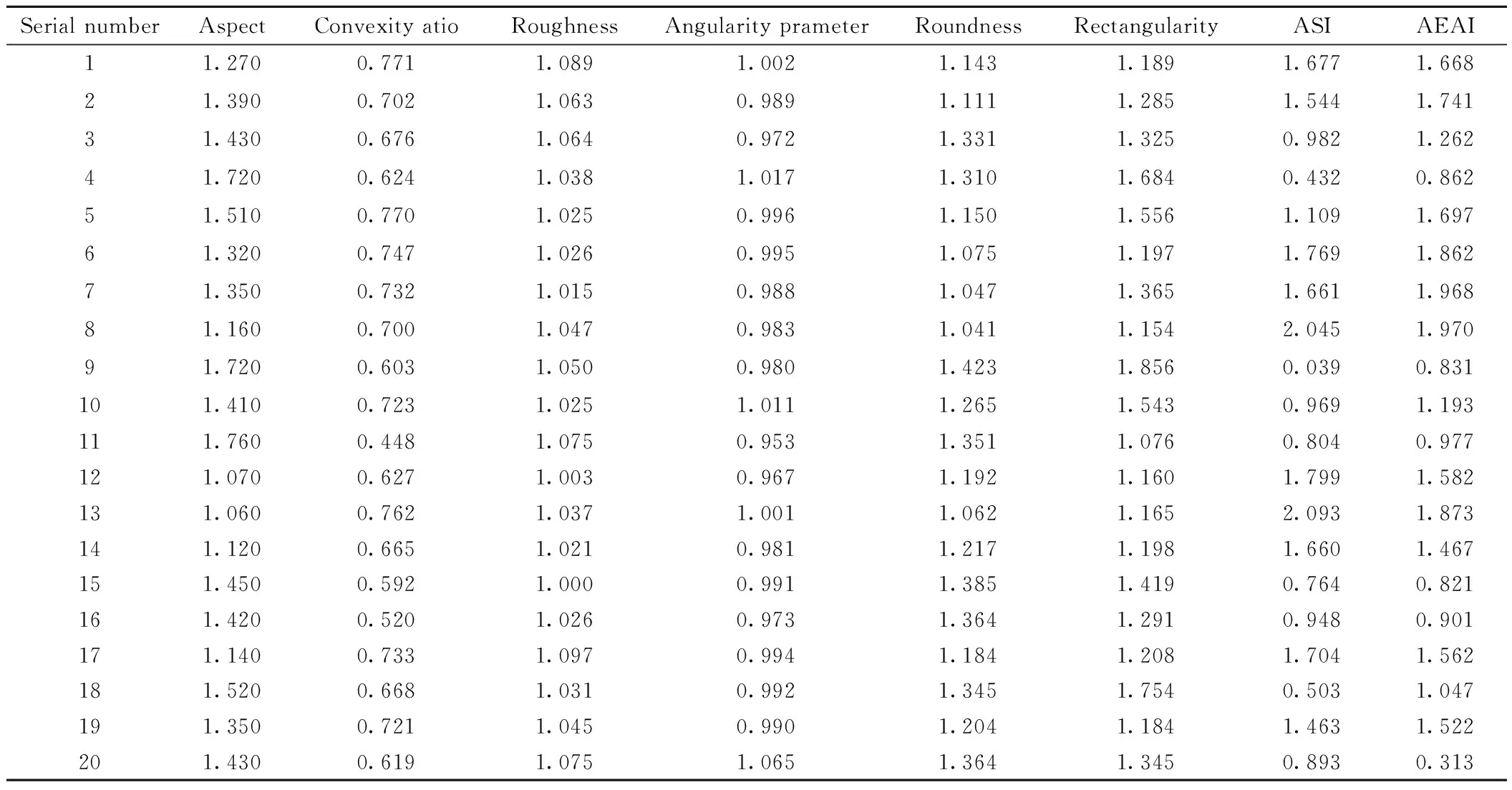
表9 部分ASI和AEAI指标值

由表9可知,ASI的范围为[0.002 3,2.093],AEAI的范围[0.054 3,1.970],综合形状的指标值越大,粗集料越接近于球体,指标越小,越接近于针片状;综合棱角的指标值越大,粗集料的棱角性越丰富,指标值越小,粗集料的棱角性越差。对ASI和AEAI指标值分别进行统计分析,如图6和图7所示。

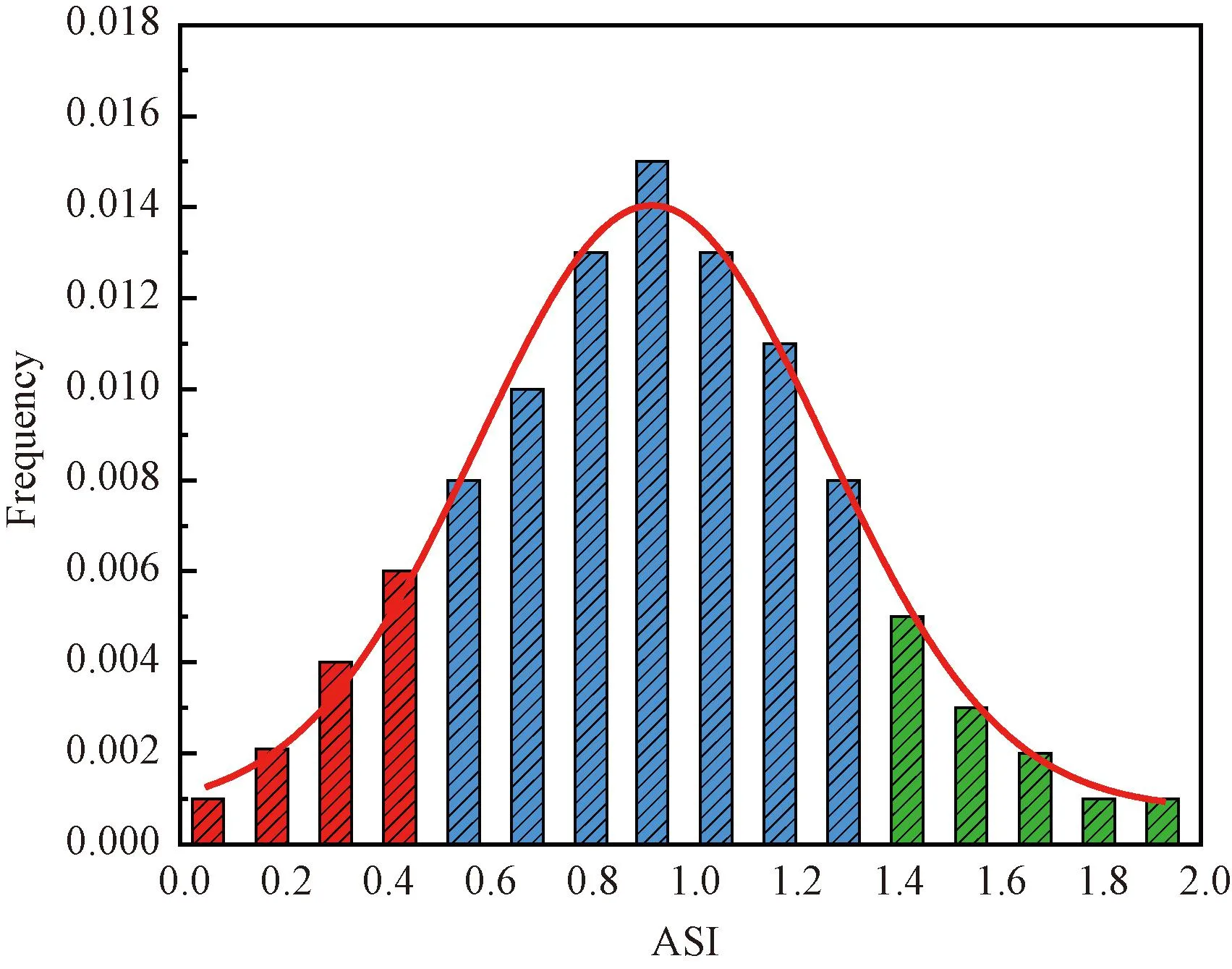
图6 ASI概率密度分布图

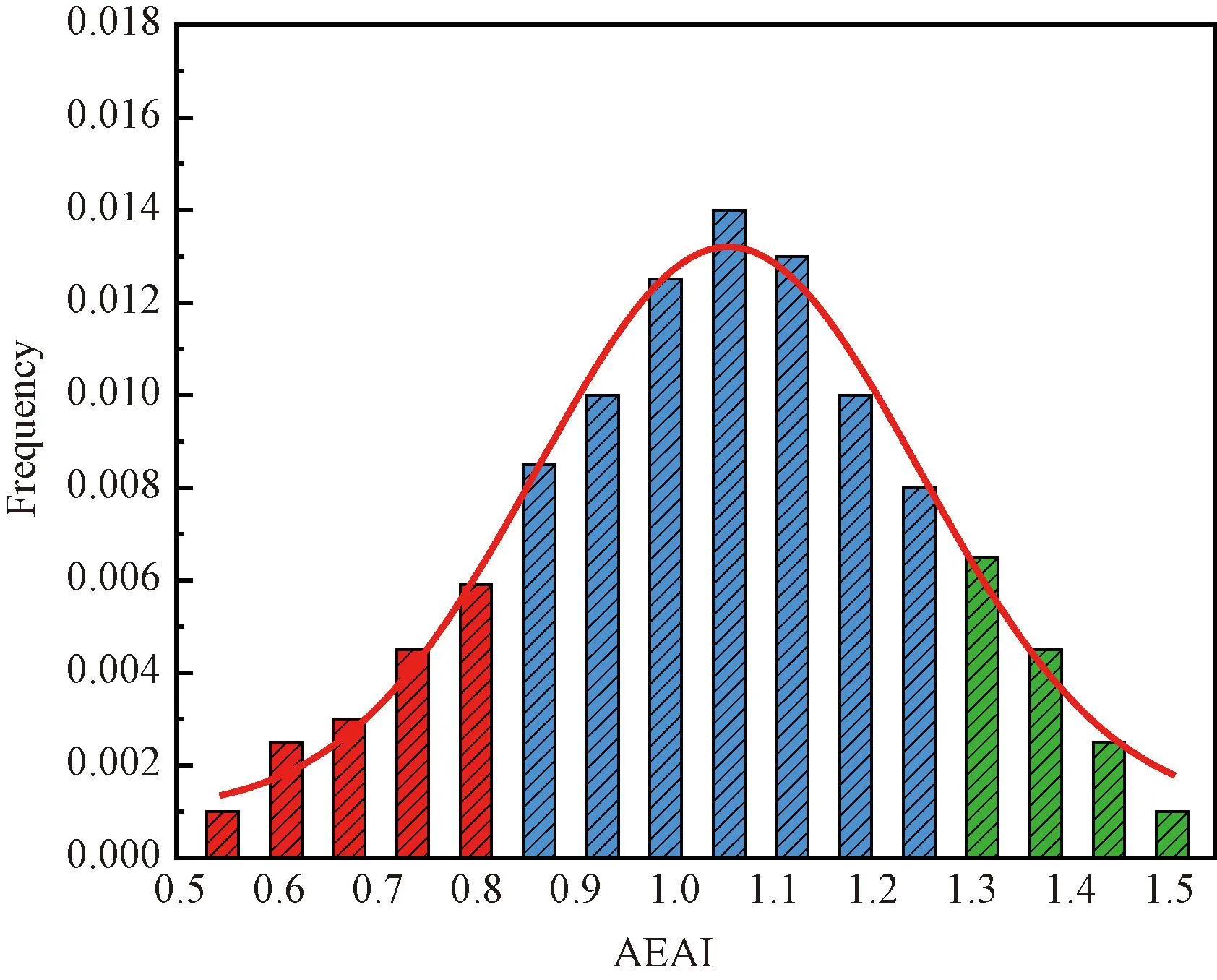
图7 AEAI概率密度分布图

从图6和7中可以看出,ASI和AEAI可以很好的表征粗集料形状和棱角的变化特征。通过计算可以得出,μASI=0.897 7和σASI=0.325 6 ,μAEAI=1.054 3和σAEAI=0.235 1。

根据拉依达准则,测试的1 800颗粗集料指标值应全部集中在(μ-3σ,μ+3σ)范围,落在这个范围之内的概率超过了99.7%,对落在±3σ之外的点予以去除,优化后的粗集料综合形状指标的区间为[0.007 8,1.965 4],粗集料综合棱角指标的范围[0.554 2,1.494 2]。

根据图8,对不同粗集料形状和棱角进行划分,当ASI的指标范围为[1.223 3,1.964 2],该粗集料为高球度,此时粗集料接近于球状或者立方体状;当指标范围为[0.572 1,1.223 3],该粗集料为中球度,粗集料较为接近于球状或者立方体状;当指标范围为[0.007 8,0.572 1],该粗集料为低球度,更接近于针片状。

图8 粗集料形状和棱角评价图 (a)ASI;(b)AEAI

同理,对于粗集料的棱角性而言,当AEAI的指标范围为[1.289 4,1.494 2],该粗集料为高棱角,此时粗集料表面棱角丰富,具有较多的破裂面;当指标范围为[0.819 2,1.289 4],该粗集料为中棱角,粗集料表面棱角性一般;当指标范围为[0.554 2,0.819 2],该粗集料为低棱角,此时粗集料表面较为光滑,更接近卵石。

4 粗集料形态综合指标合理性验证

为验证提出的粗集料综合形态指标的合理性和适用性,选用五种岩性的粗集料进行综合指标评价。待测集料的粒径为9.5～13.2 mm,其中石灰岩分别来自浙江杭州、广州肇庆和陕西渭南,玄武岩分别来自浙江丽水和广东佛山,辉绿岩分别来自广州惠州和浙江宁波,花岗岩分别来自广州惠州、重庆和广东汕头,硬砂岩来自广州梅州。首先利用第二代集料图像采集系统(AIMS-Ⅱ)测试11种不同种类岩性粗集料的球度和梯度棱角,比较不同种类粗集料的形状特征和棱角特征,绘制粗集料球度和梯度棱角的分布图,如图9所示。

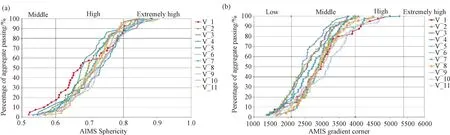
图9 AIMS-Ⅱ指标测试结果 (a)球度;(b)梯度棱角

从图9可知,不同类型的粗集料具有不同的球度和梯度棱角的分布特征,不同产地和不同加工方式的粗集料指标相差较大,来自广东汕头的花岗岩球度最大,浙江杭州石灰岩的球度最小,来自于重庆的花岗岩梯度棱角最大,浙江杭州石灰岩的梯度棱角最小。故可得这11种类型粗集料具有评价粗集料形态特征的合理性,对上述指标求平均值,并同时利用无损扫描设备(X-CT)[27-30]和线激光仪进行粗集料图像采集和相应的形态指标计算,求得该粗集料的指标平均值,见表10。

表10 不同设备粗集料指标平均值

将基于线激光的综合评价指标方法所得的结果与AIMS-Ⅱ和X-CT测试的指标进行对比分析。以粗集料综合形状和棱角指标为X轴,以AIMS-Ⅱ和X-CT测试的指标值为Y轴,进行不同评价指标的线性拟合,并计算R2值,所得的拟合曲线如图10所示。

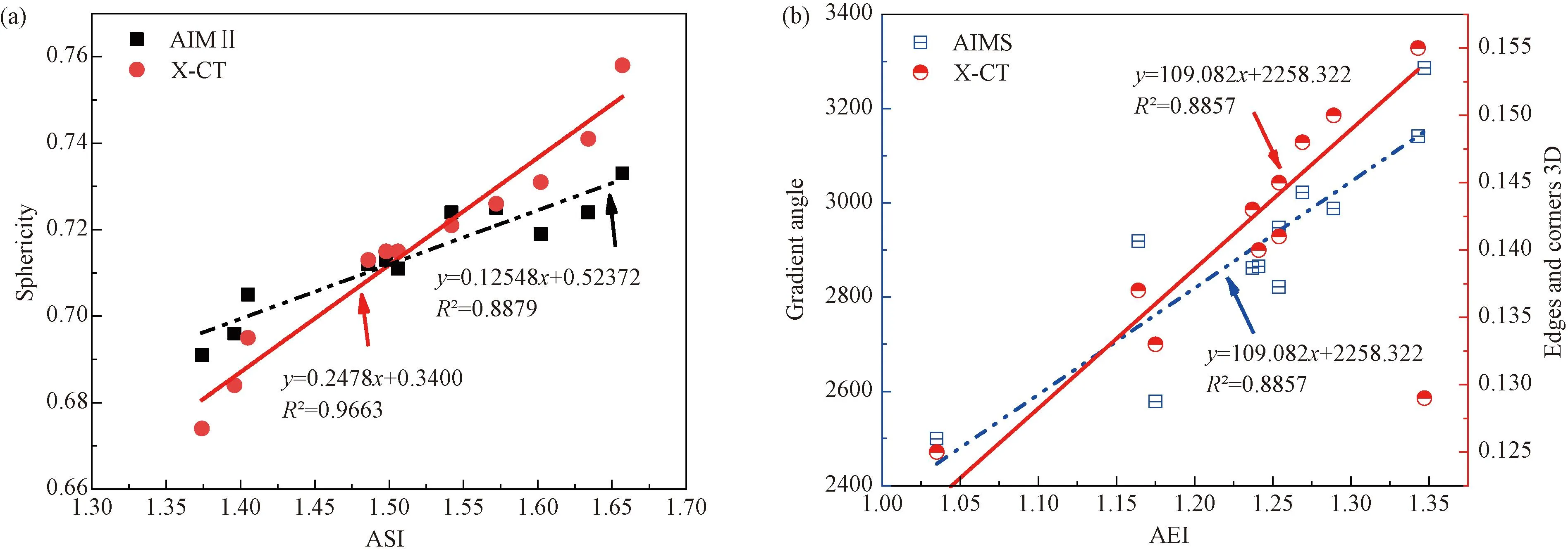
图10 粗集料形态评价指标与其他指标的相关性(a)ASI 和SP的相关性分析;(b)AEAI 与 GA、3DA的相关性分析相关性分析

由图10(a)分析得到,ASI指标与X-CT测试指标、AIMS-II测试指标的相关系数R2分别为0.966 3、0.887 9,具有较强的线性关系。由图10(b)分析得到,AEAI指标与X-CT测试指标、AIMS-II测试指标的相关系数R2均为0.885 7,具有较强的线性关系。所以提出的粗集料形态综合指标具有较高的合理性。且该指标也适用于不同岩性粗集料的形状和棱角表征。

与此同时,对上述结果进行方差分析测试,确定粗集料形状和棱角在各种测试方法中结果之间的差异,通过Spearman秩相关系数的计算,进一步说明所提出的粗集料形态综合指标的可靠性和合理性。Spearman的排名秩相关系数q的计算公式为[31]：

(7)

式中：n为样本大小,x和y分别表示视觉排名结果和图像分析结果排名。Spearman秩相关系数的值介于-1到1之间。Spearman秩相关系数为零,表示X和Y之间没有相关性(x和y分别为X和Y的等级),而Spearman秩相关系数接近1,即使X和Y之间不是线性关系,也显示出单调相关的关系。

各种测试手段的Spearman秩相关系数分析结果见表11。