让学生拥有良好的数学表达能力

朱亦冰

摘 要：学生良好的数学表达能力体现于数学交流和数学思维能力，而这种能力的形成取决于合理的经验积累.日常教学实践中，教师有意识地通过问题情境、多元表征和范式训练等方式可以强化经验的训练和积累，对学生良好数学表达能力的提升至关重要.

关键词：数学表达能力；问题情境；多元表征；范式训练

数学表达是师生互动和生生交流的基础，理性而精炼的数学表达能力可以让学生更好地思考、更流畅地交流，可以让数学学习更高效、更深入.学生数学表达能力的提升过程是通过适当引导、规范语言训练等方式，让学生掌握好运用数学语言表达自身想法的方法，获得表达能力的逐步提高，逐渐丰富语言水平，最终能达到正确合理、自主灵活表达的过程^［1］.而在此发展过程中，有效的经验支持对于能力的提升至关重要.

1 问题情境是促进表达能力萌发的基础

问题可以激起学生表达的欲望，好的问题更是促使学生“融入”课堂活动、积极表达的助推器.这就需要教师基于数学知识的本质，创设学生喜欢的、激活数学思维的问题情境，促进良性对话机制的形成，让学生轻松愉悦地探索问题，自主自发地进行表达，为表达能力的萌发打下坚实基础.

案例1：分数的初步认识（二）

本节课教师设计了大问题板块教学，以下为第一板块：为什么都是这一盘桃的二分之一？

师：为什么？

生1：我认为这里的每盘桃都是平均分为2份，不管一盘有多少个，即便是20个，也是将其平均分为2份，其中的一份就只能是它的二分之一.

生2：是的，即便这盘桃有100个，平均分为2份，每一份也只能是这盘桃的二分之一.

生3：我有新发现，如果是双数，平均分为2份，那每一份即为它的二分之一.

师：生3有了新的想法，他认为双数才能成立，那这盘桃的个数若为单数，它的二分之一还能表示出来吗？（学生陷入沉默，一些学生在思考后有了想法）

生4：单数有何不可？若这盘桃有3个，那就将其中1个桃分为两半，则其中一份就是一个半.

生5：我认为无论多少个都可以.

生6：不管多少个都可以想象成一个大大的桃子，将其平均分为2份即可.

师：生6的想法很有創意，其实不管多少个，我们都可以将其看作一个整体……

以上教学片断中，教师从教学重难点着手，基于具体学情创设指向核心概念的大问题情境，让学生从自己已有的知识储备和生活经验出发去理解和感知分数，在学生亲历了思考、探索、猜想、倾听、争辩、讨论等学习过程后，抽象的数学概念从模糊走向了清晰，知识的本质逐渐显露头角.这里，也正是因为教师给予了学生自由发挥的空间，让他们的全身心都处于主动学习的兴奋之中，使得他们的语言表达能力自然萌发.

2 多元表征是强化理性表达的筹码

数学表达具有学科性这一点毋庸置疑，那么除去清晰表达，还需从数学学科本身出发，联系多种数学语言，通过多元表征来强化理性表达.这就需要教师利用好文字语言的直接和图形语言的直观，让学生理性探寻适当的表达形式，清楚表达自己的观点，形成丰富的表达方式，提升自身的数学学习能力.

案例2：5的倍数的特征

师：下面我们思考这样一个问题：为什么5的倍数只看个位？

生1：可以举例，例如10，首先1+0=1，然后呢，然后……

师：你们明白生1的意思吗？尽管不太明白，但是可以肯定的是他的发言中有可取之处，是什么？

生2：可以举例.

师：非常好，你们觉得这个办法好不好？

生（齐）：好.（大家都向生1投去赞许的目光）

师：不过，下一次在思考的同时我们还需要考虑一下表达的方法，这样就完美了！有没有其他同学替他来表达一下呢？

生2：首先列举一位数，即5×1=5，5是5的倍数；接着列举两位数，即5×2=10，10也是5的倍数；然后列举三位数，如125除以10，商是12余5，5是5的倍数，可见125也是5的倍数.

生2：我知道，生1所说的就和位值原理类似，就是将一个数拆分……

师：能到讲台上来给大家讲解一下吗？（在教师的邀请下，生2大胆上台示范并讲解）

生2：例如3255，可拆分为3250与5，我们都知道3250是10的倍数，10又是5的倍数，因此只需考虑个位上的5就可以了.

师：你们给予了如此热烈的掌声，应该是大家都听懂了，谁来说一说你为什么鼓掌呢？

生3：我觉得他运用列举法讲解得很有道理，也很有条理，而且他用的是10的倍数讲解的，我觉得很好.

师：生2的确表达得很好，那对于他的想法你们还有补充的地方吗？

生4：假设一个四位数是abcd，即abcd=1000a+100b+10c+d，因为1000a、100b、10c均为10的倍数，而10自然是5的倍数，所以它们就都是5的倍数，最后只需要考虑个位上的d是否为5的倍数即可.（教室里再一次掌声如雷）

本节课中教师抛出的问题难度较大，因此需要极好地引导和表达.从而在教师的循循善诱下，学生经历了拾阶而上的表达历程，从文字语言到图示语言，并借助于算珠，最终完成了运用符号表示四位数的严密推理过程，真正意义上完成了经验归纳到逻辑推理的进阶.此处，从生1的表达不清，到最后生4的清晰表达，离不开教师为学生打造的展示舞台，也充分展现了多元表征下学生数学语言的智慧.

3 范式训练是精炼表达的保障

数学表达能力的形成与提高并非一蹴而就，需要一以贯之地系统培养.小学生正处于数学语言训练的关键期，他们的数学表达往往缺乏条理且呈现碎片式，而小学生模仿能力很强，提供范式训练对于他们精炼表达十分有效^［2］.因此，每一节课中，教师需要以自身精准的表达范式和精炼的数学素养为指导，为学生提供充分的表达范式，让学生在长期的熏陶下培养良好的数学语言表达能力.

案例3：认识平均分

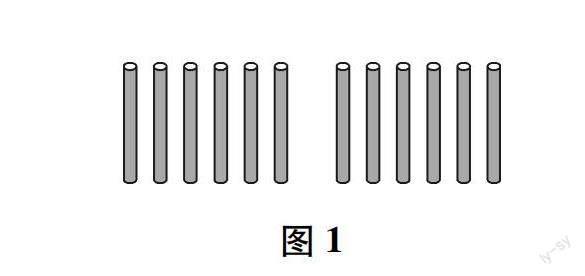
问题：如图1所示的12根小棒，你觉得还可以如何平均分？

活动设计：

活动1：圈一圈，并记录你的所思所想.

活动2：组内4人先每人思考一种分法，后相互交流.（交流过程中可以这样去表达：我是这样分的……我认为这就是平均分，因为……）

师：在探讨之后，你们一定有很多想法，谁愿意先来说一说？

生1：我是这样分的，将12根小棒按照每份1根分，可分为12份.我认为这就是平均分，因为每一份都是1根，都一样多.

生2：我是这样分的，将12根小棒按照每份2根分，可分为6份.我认为这就是平均分，因为每一份都一样多.

……

师：你们已经有了每一份1根、2根、3根、4根、6根的思路，那每一份5根可以吗？

生3：如果5根5根地分，两个5根就是10根，还有一份只有2根了，那么就不是5根了，所以这样分不是平均分.

表达训练时，教师的范式引导是学生精确表达的保障，它可以帮助学生建立言之有理的语言模式，也可以促进学生养成说理的好习惯，还可以极好地孕育思维素养^［3］.这是一个推动学生精准表达的案例，案例中教师为学生打造了生动活泼的数学活动，同时也给予了学生正确的范式引导，为学生的表达提供指引，这样学生就学会了用精准的数学语言表达出数学规律，同时也能在精准表达中反思思维过程，深化对新知的认识和理解，引发更多领悟.

总之，提升学生的数学表达能力具有十分重要的意义.因此，笔者认为，有必要在数学教学中有目的、有意识地加以训练，让学生在解决问题、多元表征和范式训练中获得良好表达的方法和经验，以提高数学表达能力，让数学学习更有意义.

参考文献：

［1］ 李树臣.论形成和发展数学能力的两个根本途径［J］.中学数学教学参考，2002（9）：11-13.

［2］ 万小燕.倾听学生的思维——浅谈数学表达能力在高中数学中的有效培养［J］.中学数学，2018（9）：50-51.