基于MLS形函数处理边界的电阻率法有限单元正演模拟
2023-03-16麻昌英赵文学汤文武1柳建新闫玲玲周聪1秦臻1钟炜城程流燕
麻昌英, 赵文学, 汤文武1,*, 柳建新, 闫玲玲, 周聪1,,秦臻1,, 钟炜城, 程流燕
1 东华理工大学江西省防震减灾与工程地质灾害探测工程研究中心, 南昌 330013 2 中南大学有色金属成矿预测与地质环境监测教育部重点实验室, 长沙 410083 3 东华理工大学地球物理与测控技术学院, 南昌 330013
0 引言
有限单元法(Finite element method, FEM)在求解区域内根据节点拓扑关系剖分单元,基于单元节点在单元内进行线性或高次插值模拟场函数,具有模拟精度高,计算效率高,适应性强等特点.20世纪70年代初,Coggon (1971)首次将其引入到电法勘探正演模拟领域,国内学者徐世浙(1994)将有限单元法应用于电法勘探中,对有限单元法进行了系统的阐述.此后,有限单元法成为目前国内外电阻率法正演模拟中主要的数值模拟方法(e.g., Sasaki, 1994; 强建科和罗延钟, 2007; 柯敢攀和黄清华, 2009; Huang and Lin, 2010; Xiong et al., 2018;麻昌英等, 2014; Hu et al., 2021; 戴世坤等, 2022).近年来,针对复杂起伏地形和地下复杂目标体模拟,基于非结构化单元和自适应加密策略的有限单元法,在电阻率法、大地电磁及可控源电磁法等正演模拟中备受关注(e.g., Bing and Greenhalgh, 2001; 任政勇和汤井田, 2009; 汤井田等, 2010; Ren and Tang, 2010; Tang et al., 2010, 2015; Vachiratienchai and Siripunvaraporn, 2013; 韩骑等, 2015; 蔡红柱等, 2015; 吴小平等, 2015; Yan et al., 2016; Chou et al., 2016; 李勇等, 2017; 陈汉波等, 2018; 曹晓月等, 2018; Ren et al., 2018; 赵宁等, 2019; Guo et al., 2022),借助于图形几何学相关单元剖分器实现任意节点分布的非结构化网格剖分,可适应起伏地形和地下目标体的复杂形态变化,并利用后验误差策略指导单元自适应加密,仅需建立初始单元模型,正演过程中可在需要的局部区域自适应加密单元提高模拟精度,为推进高灵活性、高精度的正演模拟研究发展做出了卓越贡献.
有限单元法采用单元节点在单元内构造线性或高次形函数对场函数进行分片插值,因此有限单元法中网格单元剖分不可避免,单元之间模拟的场函数连续性欠佳.Lancaster和Salkauskas(1981)在研究曲面和曲线的拟合时,基于传统的最小二乘近似理论,提出了移动最小二乘法(Moving Least Square, MLS)构造形函数(MLS形函数),相比于有限单元法形函数,MLS形函数具有良好的连续性,在有限单元法后处理中也得到了应用(Tabbara et al., 1994; Tang et al., 2021).基于MLS形函数,Belytschko等(1994)在扩散元法及对近似导数确定,强加本质边界条件及数值积分处理等问题改进的基础上提出了无单元法(Element free method, EFM).无单元法不再需要基于节点拓扑关系的网格单元剖分,自提出之后在多个正演模拟领域得到了广泛应用.在地球物理领域方面,无单元法中的无单元Galerkin法(Element free Galerkin method, EFM)在地震波场(Jia and Hu, 2006; 王月英, 2007; Jie et al., 2008)、探地雷达(戴前伟和王洪华, 2013; 冯德山等, 2013; Feng et al., 2015)和大地电磁(苏洲等, 2012; 严家斌和李俊杰, 2014; 嵇艳鞠等, 2016)等正演模拟研究中已取得了良好的研究成果,展示了无单元Galerkin法在地球物理勘探领域的有效性.在电阻率法正演模拟中,麻昌英等(麻昌英等, 2017, 2018; Ma et al., 2019)分别利用径向基点插值(RPIM)形函数和移动最小二乘(MLS)形函数研究了2.5维电阻率法无单元Galerkin法正演,实现了任意复杂形体、地形起伏、局部节点加密的电阻率法正演模拟.以上研究成果表明,无单元Galerkin法突破了传统数值模拟方法受单元约束的限制,与传统数值模拟方法相辅相成,具有高灵活性、高适应性、高精度等特点,特别适用于任意复杂地电模型正演,在地球物理领域具有良好的发展前景.然而,无单元法通常采用高斯积分求积,由于无单元法的近似函数一般为有理函数而不是多项式,为了保证模拟精度须使用较多的高斯点和较高阶的高斯积分点进行计算(Dolbow and Belytschko, 1999),同时需要为每一个高斯积分点构造形函数,而无单元法计算量与积分点数量成正比,这将导致无单元法计算量大,计算效率低(麻昌英等, 2017),在实际应用中受到了一定的限制.
在电阻率法正演模拟中,现有正演模拟方法中采用第一类边界条件时,认为截断边界上场值为零,需要足够大的计算域以满足第一类边界条件.采用第三类边界条件(即混合边界条件)时,为降低边界对模拟精度的影响,通常仍要求截断边界与供电点距离较大,通过扩大计算域来降低截断边界影响(阮百尧等, 2001; 黄俊革等, 2003; 麻昌英等, 2018),这使得建模难度和计算量增加,期望进一步探索建模更方便且计算量更少的方法.Blome等(2009)采用无限元法处理边界问题,与Dirichlet和混合边界条件相比缩小了计算范围要求.汤井田和公劲喆(2010)在有限元-无限元法三维电阻率法正演中,提出了一种最优的无限元形函数,并其与非结构化四面体有限元相结合,取代了传统混合边界条件,使得电位在无限域内连续并在无限远处衰减为零,该方法可以在近似测区大小的计算范围内得到与混合边界条件相当的计算精度,优于相同计算范围下齐次边界条件的解,有利于减少计算节点数.Ren和Tang (2014)在三维电阻率法有限单元正演中,多电极情况下将处于所有供电电极近似中间位置作为中心点,在计算域足够大时将该中心点计算边界条件近似代替所有电极的边界条件,建立统一的多电极系统边值问题,使多电极情况下具有共同的系统矩阵.Yuan等(2016)在电阻率法有限单元2.5维正演中,采用一种新型的无限元形函数来代替无穷远边界上的传统混合边界条件,有效减少了因人为施加边界条件不适当而引起的数值误差,并且最终系统矩阵是稀疏的、对称的,并且与源电极无关.张钱江等(2016)在三维电阻率法有限单元正演中提出了一种近似边界条件方法,该方法将与场源位置相关的边界系数矩阵从刚度矩阵中分离出来,使得分离后的刚度矩阵与场源位置无关,并将边界系数矩阵与边界处一次电场向量的乘积移到线性方程组右端项中,当场源位置发生改变时,只需要重新计算右端项就可以实现快速回代求解,数值精度优于混合边界条件.
基于戴前伟和王洪华(2013)、Feng等(2015)、Ma等(2019)提出的探地雷达和电阻率无单元Galerkin法正演中的移动最小二乘(MLS)形函数,本文将MLS形函数应用于电阻率法有限单元法正演的第三类边界条件处理,以期望进一步降低正演模拟对计算域范围要求.在此基础之上,提出电阻率法有限单元-移动最小二乘(FEM-MLS)耦合正演算法.通过不同模拟方法对层状模型测深和异常体模型进行模拟对比,验证了本文算法的有效性,结果表明采用第三类边界条件时,本文提出的FEM-MLS耦合法相比于有限单元法,在满足精度要求情况下可进一步缩小计算域,在小范围计算域内便可获得较好的正演模拟精度,并提高了计算效率,具有更好的模拟性能.
1 基于三角形单元的电阻率法有限单元法正演
当采用第三类边界条件时,2.5维电阻率法波数域总电位U(x,λ)的边值问题及其对应的变分问题分别表示为(1)和(2)式(徐世浙,1994):
(1)
(2)
(1)和(2)式中σ为介质电导率,λ为波数,I0为电流,δ(A)为狄拉克函数,A为场源点,K0、K1分别为第二类零阶、一阶修正贝塞尔函数,Ω为问题域(全局域),Γs为地表边界,Γ∞为截断边界,rA为场源点到截断边界的点的距离,n为边界单位外法向,cos(rA,n)为n与矢径rA构成的夹角余弦.为了更好模拟复杂几何地质体和起伏地形,采用非结构化三角形单元剖分计算域.有限单元法求解上述变分问题相关理论已非常成熟,通过线性插值和对(1)式第一式求变分(Zienkiewicz and Taylor, 1989; 徐世浙, 1994),在每个三角单元Ωe内(1)式等价为(3)式.
KeUe=Fe,
(3)
式中Ke=Ke1+Ke2+Ke3为有限单元法单元子刚度系数矩阵,其中Ke1和Ke2对应(2)式中的体积分,Ke3对应截断边界积分,Fe为右端项.本文对有限单元法中截断边界进行研究,Ke3表达式为
(4)

Ke3=(Ke3ij),i,j=1,2,3
(5)
式中的各个元素表达式写为
(6)
式中
(7)

(8)
(9)

KFEUFE=F,
(10)
式中KFE为由全部三角单元子域Ωe的Ke相加组成的有限单元法总系数矩阵,UFE为有限单元法所有三角单元节点上的波数域电位子向量Ue组合成的列向量,F为有限单元法方程右端项列向量.
2 移动最小二乘近似
利用移动最小二乘(Moving Least Square, MLS)近似构造的形函数已在无单元法中被广泛应用.无单元法正演模拟中,需要为计算域Ω中任意点xT=(x,z)构造局部支持域Ωq,假设Ωq中包含有n个节点{x1,x2,…,xn},它们对应的波数域电位值为{U1,U2,…,Un}.假设计算域Ω中波数域电位函数U(x),则计算域内任意一点x处U(x)的MLS近似表达式为
(11)
式中,p(x)为坐标xT=(x,z)的基函数向量,本文采用线性基函数pT(x)=(1xz).(11)式中a(x)为近似插值的系数向量,具体表示为
aT(x)=[a1(x)a2(x)a3(x)].
(12)
利用最小二乘法对(11)式进行推导(Liu and Gu, 2005; 冯德山等, 2013; Ma et al., 2019),最后得到
ΦT(x)=[φ1(x)φ2(x) …φn(x)]
=pT(x)A-1(x)B(x),
(13)
式中Φ(x)为计算点x的支持域中n个节点的MLS形函数向量.A(x)为基函数加权后形成的系数矩阵,定义为
(14)


图1 移动最小二乘近似示意图Fig.1 Sketch showing the moving least squares approximation
B(x)=[w(r1)p(x1)w(r2)p(x2)…w(rn)p(xn)].
(15)
在移动最小二乘形函数中,其系数a(x)为坐标x的函数,这使得该加权最小二乘近似可连续移动,故只要合理选择连续的权函数,则移动最小二乘形函数在全局计算域内是连续的,其全局连续特性对于连续场的正演模拟是有利的.在无单元法正演模拟应用中,指数函数和样条函数常被作为权函数,本文中采用形式如(16)式的三次样条函数作为权函数(Liu and Gu, 2005; Ma et al., 2019),它具有二阶连续性.
(16)
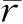
(17)
式中d=|x-xi|为计算点x与支持域内节点xi的距离,rw为权函数域尺寸.
3 MLS形函数处理边界


(18)
式中,Φ为MLS形函数向量,(18)式展开得到
(19)

(20)
对于单个高斯点,子边界系数矩阵Ke3的元素表达式为
(21)
式中,i,j=1,2,…,n表示支持域Ωq中的节点局部编号.高斯点处电导率采用MLS形函数插值(22)式计算获得.
(22)

4 模型算例
4.1 层状模型
采用具有解析解的三层电阻率模型验证本文算法的有效性.建立水平方向宽380 m(X:-190~190 m),垂直方向深108 m(Z:0~108 m)的矩形计算域Ω1.如图2所示,在地表设置52根电极作为供电和观测电极,在地表X=0处进行对称四极装置测深观测.计算域Ω1及其节点分布如图3a所示,采用不规则分布的节点将计算域离散,节点在靠近电极和地层界面区域采用密集的节点分布,其他区域采用稀疏的节点分布,总节点数为14280.首先基于非结构化三角形单元的有限单元法(FEM)对22组不同收发距(AB/2)对称四极装置测深观测进行正演模拟.本文利用具有高精度的汉克尔变换计算三层电阻率模型对称四极装置测深的解析解(蔡盛, 2014).

图2 三层电阻率模型和对称四极装置测深观测示意图Fig.2 Sketch showing the three-layer resistivity model and symmetrical quadrupole device

图3 三层电阻率模型计算域Ω1(a)和Ω2(b)及其节点分布示意图Fig.3 Sketch showing the nodal distribution of three-layer resistivity model and computational domains Ω1 (a) and Ω2 (b)
如图3b在计算域Ω1的基础上,采用快速延伸的节点扩展计算域,形成计算域Ω2,水平方向宽超过2000 m,垂直方向高超过超过1000 m,共16800个节点.对计算域Ω1分别采用有限单元法和FEM-MLS耦合法进行电阻率法对称四极测深模拟,对计算域Ω2采用有限单元法模拟.采用FEM-MLS耦合法时,边界积分计算中在子边界上使用两个高斯点计算,使用三角形单元的三个节点作为高斯点支持域.
图4和图5分别为中间层为高阻和低阻时,不同方法和不同计算域的正演视电阻率和相对误差曲线.由图4和图5的正演视电阻率和相对误差曲线分析可知,无论中间层为高阻或低阻,有限单元法采用计算域Ω1时,正演视电阻率曲线尾部数值偏低,相对误差较大,FEM-MLS耦合法采用计算域Ω1和有限单元法采用计算域Ω2时,正演视电阻率曲线尾部模拟精度明显得到改善,模拟结果与解析解吻合很好.表1为不同方法和不同计算域正演视电阻率平均相对误差,相比于有限单元法采用计算域Ω1,FEM-MLS耦合法采用计算域Ω1和有限单元法采用计算域Ω2时均可有效提高模拟精度,它们的平均相对误差均小于1%,且相差很小.上述分析表
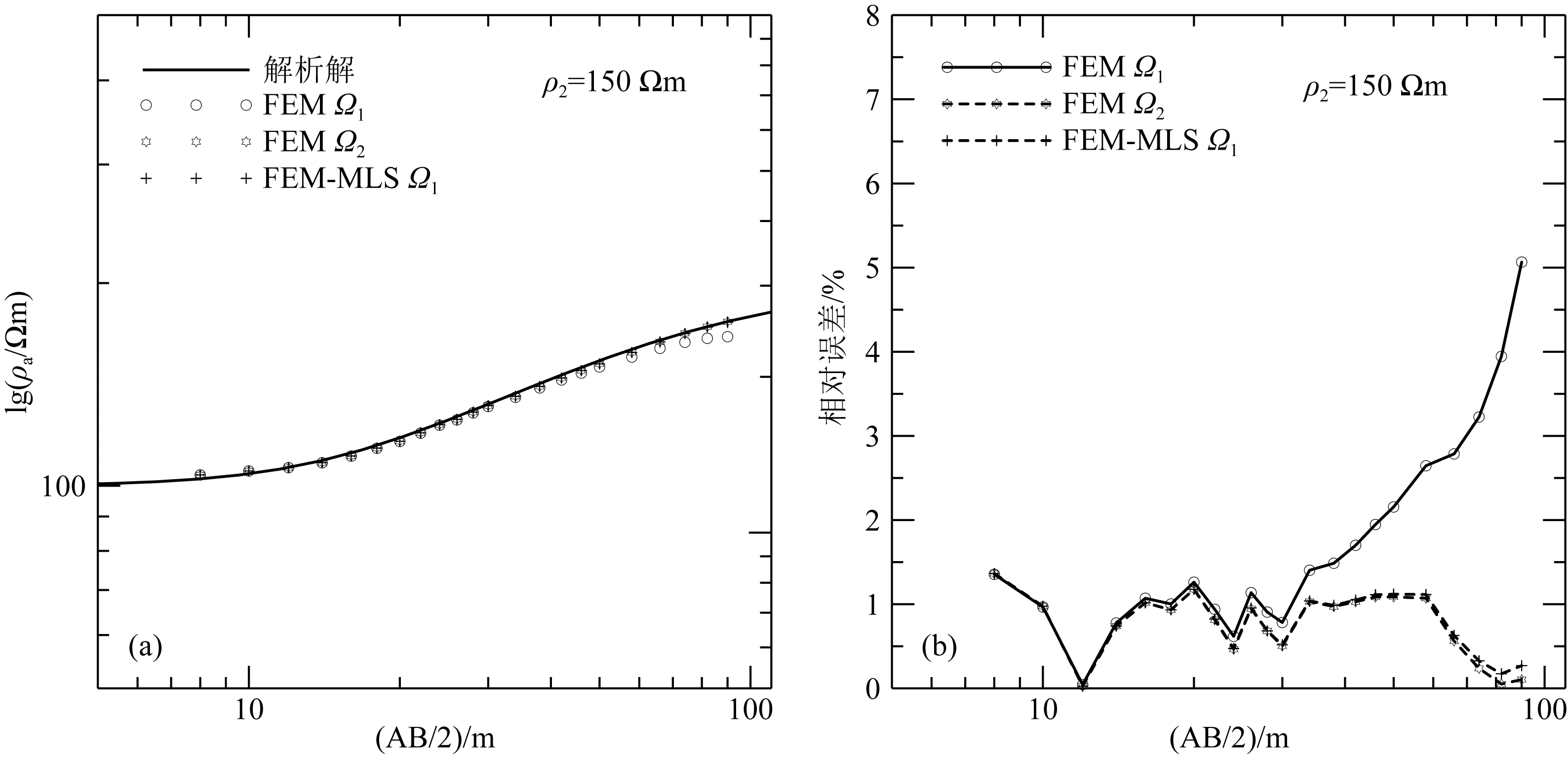
图4 中间层为高阻时三层电阻率模型模拟视电阻率(a)和相对误差(b)曲线Fig.4 The apparent resistivity and relative errors of three-layer resistivity model with the resistance middle layer(a) Apparent resistivity; (b) Relative errors.

图5 中间层为低阻时三层电阻率模型模拟视电阻率(a)和相对误差(b)曲线Fig.5 The apparent resistivity and relative errors of three-layer resistivity model with the conductive middle layer(a) Apparent resistivity; (b) Relative errors.
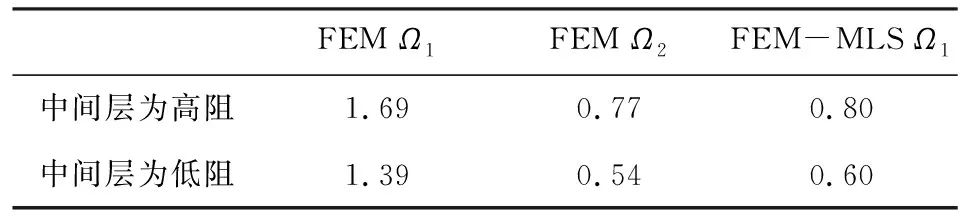
表1 不同方法和不同计算域三层模型测深视电阻率平均相对误差(%)Table 1 The relative errors (%) of three-layer resistivity model by using different methods and computational domains
明,通过扩边减小边界的影响可有效提高有限单元法模拟精度,FEM-MLS耦合法可在较小范围计算域内获得良好的模拟精度,与有限单元法采用扩边后的计算域正演模拟效果相当,相比于采用相同较小范围计算域的有限单元法平均精度(平均相对误差)提高了约一倍,验证了FEM-MLS耦合法的有效性.因此FEM-MLS耦合法可使用较小的计算域便可获得良好的模拟精度,相比于有限单元法不需要扩边处理,可使得正演建模更加方便,使用更小的计算域也使得计算量更小,提高正演模拟效率.
为了研究FEM-MLS耦合法中MLS形函数计算边界积分时参数选择与模拟精度的关系,首先在子边界上分别采用高斯点数G=2,4,6对三层模型对称四极测深模拟,使用三角形单元的三个节点作为高斯点支持域,采用计算域Ω1计算.图6和图7分别为中间层为高阻和低阻时,采用不同高斯点数的正演视电阻率和相对误差曲线.由图6和图7分析可知,无论中间层为高阻或低阻,采用不同高斯点数获得正演视电阻率和相对误差基本是重合的,表明采用不同高斯点数模拟精度基本一致,同等条件下高斯点数对边界积分影响不大.因此,为减少计算量在子边界采用两个高斯点计算边界积分.

图6 中间层为高阻时不同高斯点数三层电阻率模型模拟视电阻率(a)和相对误差(b)曲线(a) 视电阻率; (b) 相对误差.Fig.6 The apparent resistivity and relative errors of three-layer resistivity model with the resistance middle layer by using different number of Gauss points(a) Apparent resistivity; (b) Relative errors.

图7 中间层为低阻时不同高斯点数三层电阻率模型模拟视电阻率(a)和相对误差(b)曲线.Fig.7 The apparent resistivity and relative errors of three-layer resistivity model with the conductive middle layer by using different number of Gauss points(a) Apparent resistivity; (b) Relative errors.
分别采用支持域节点数D=2,3,4,其中当D=2时为采用子边界端点对应的2个节点,即支持域两个节点全为子边界端点,当D=3时为使用三角形单元的三个节点,当D=4时为处三角形单元的三个节点外,加上距离高斯点最近的一个节点.图8和图9分别为中间层为高阻和低阻时,支持域采用不同节点数的正演视电阻率和相对误差曲线.由图8和图9分析可知,无论中间层为高阻或低阻,支持域采用不同节点数获得正演视电阻率和相对误差基本是重合的,支持域采用不同节点数模拟精度基本一致,表明同等条件下FEM-MLS耦合法边界积分中支持域采用不同节点数对边界积分影响不大.支持域内在包含单元三个节点基础上若再增加节点数时(D>3),模拟结果与解析解也基本吻合(基本与上述模拟结果重合,因此未图示模拟结果),支持域节点数增加意味着计算量增加.
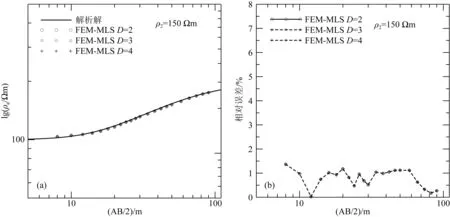
图8 中间层为高阻时支持域不同节点数三层电阻率模型模拟视电阻率(a)和相对误差(b)曲线Fig.8 The apparent resistivity and relative errors of three-layer resistivity model with the resistance middle layer by using different number of nodes in the support domain(a) Apparent resistivity; (b) Relative errors.

图9 中间层为低阻时支持域不同节点数三层电阻率模型模拟视电阻率(a)和相对误差(b)曲线Fig.9 The apparent resistivity and relative errors of three-layer resistivity model with the conductive middle layer by using different number of nodes in the support domain(a) Apparent resistivity; (b) Relative errors.
为了研究FEM-MLS耦合法中MLS形函数计算边界积分时支持域节点位置与模拟精度的关系,当D=2时,采用子边界端点其中对应的一个节点和三角形单元非子边界上的一个节点作为支持域,即支持域两个节点非全为子边界端点.图10和图11分别为中间层为高阻和低阻时正演视电阻率和相对误差曲线.由图10和图11分析可知,无论中间层为高阻或低阻,当支持域两个节点全为子边界端点时模拟结果与解析解吻合很好,相对误差较小,而当支持域两个节点全非为子边界端点时正演视电阻率曲线尾支与解析解出现一定的偏离,相对误差曲线尾支逐渐增大,模拟精度下降.
通过上述模拟结果分析表明,当采用MLS形函数计算边界积分时,在同等情况下,FEM-MLS耦合法中子边界上使用不同的高斯点数对模拟精度影响不大,采用不同高斯点数时模拟结果基本一致;高斯点支持域内采用不同节点数及其组合形式时对模拟精度影响较大,其中当子边界端点对应的两个节点不全被包含于支持域内时,可明显降低收发距相对较大时的模拟精度.因此,在采用FEM-MLS耦合法模拟时,需确保子边界两个端点对应的节点均包含于支持域内.此外,由于仅采用子边界端点对应的两个节点作为支持域时,两个节点在同一直线上,有可能使得MLS形函数构造不稳定,而若采用较多支持域节点时则需要更多的节点搜索.直接采用三角形单元的三个节点作为支持域无需额外构造支持域,同时只要三角形单元形状非特别尖锐情况下,通常可保证MLS形函数构造稳定性.基于本小节对三层地电模型模拟结果分析,FEM-MLS耦合法可采用三角形单元的三个节点作为支持域构造MLS形函数,子边界上采用两个高斯点计算边界积分,在确保模拟精度前提下以减少计算量和保证计算稳定性.

图10 中间层为高阻时支持域采用2个节点三层电阻率模型模拟视电阻率(a)和相对误差(b)曲线Fig.10 The apparent resistivity and relative errors of three-layer resistivity model with the resistance middle layer by using two nodes in the support domain(a) Apparent resistivity; (b) Relative errors.

图11 中间层为低阻时支持域采用2个节点三层电阻率模型模拟视电阻率(a)和相对误差(b)曲线Fig.11 The apparent resistivity and relative errors of three-layer resistivity model with the conductive middle layer by using two nodes in the support domain(a) Apparent resistivity; (b) Relative errors.
4.2 水平圆柱状异常体
采用水平圆柱状异常体模型进一步测试FEM-MLS耦合法的模拟性能.建立水平方向宽200 m(X:-100~100 m),垂直方向高100 m(Z:0~100 m)的计算域Ω1,背景介质电阻率ρ1=100 Ωm,在模型中添加一个水平圆柱状异常体,其电阻率为ρ2=1000 Ωm或ρ2=10 Ωm,水平圆柱状异常体圆心位于(x,z)=(0 m, 15 m),半径为5 m,水平圆柱状异常体模型和节点分布如图12a所示,共12038个节点.如图12b所示,在计算域Ω1的基础上,采用快速延伸的节点扩展计算域,形成计算域Ω2,水平方向宽超过2000 m,垂直方向高超过1000 m,共13872个节点.对计算域Ω1分别采用有限单元法(FEM)和FEM-MLS耦合法进行电阻率法对称四极测深模拟,对计算域Ω2采用有限单元法模拟.

图12 水平圆柱状异常体模型不同计算域Ω1~Ω5及其节点分布示意图(a)—(e) 分别为计算域Ω1~Ω5.Fig.12 Sketch showing different computational domains Ω3~Ω5 and the nodal distribution of the horizontal cylindrical anomaly model(a)—(e) is computational domains Ω3~Ω5, respectively.
图13为有限单元法采用计算域Ω1正演的模拟结果,图14为有限单元法采用计算域Ω2正演的模拟结果,图15为本文FEM-MLS耦合法采用计算域Ω1正演的模拟结果.基于4.1节层状模型分析结论,将有限单元法采用计算域Ω2正演的模拟结果图14作为参考模拟结果.对比分析图13和图 14可知,有限单元法两种计算域的模拟结果有明显的差异,采用计算域Ω1正演的模拟结果与层状模型类似,在收发距(AB/2)相对较大时正演视电阻率偏低,模拟精度较差.对比分析图14和图15可知,FEM-MLS耦合法采用计算域Ω1正演的模拟结果与参考结果基本相同.以参考结果(图14)为基础,计算FEM-MLS耦合法采用计算域Ω1正演的模拟结果相对误差,相对误差分布如图16所示.由图16分析,无论异常体为高阻还是低阻,相对误差均很小,异常体为高阻时最大相对误差不超过0.06%,异常体为低阻时最大相对误差不超过0.05%,表明FEM-MLS耦合法在较小范围计算域条件下可获得良好的模拟精度,进一步验证了FEM-MLS耦合法的有效性.

图13 不同电阻率异常体有限单元法采用计算域Ω1获得的视电阻率拟断面图(a) 高阻水平圆柱状异常体; (b) 低阻水平圆柱状异常体.Fig.13 The apparent resistivity of forward modeling results by using the FEM method with computational domain Ω1(a) Resistance anomaly; (b) Conductive anomaly.
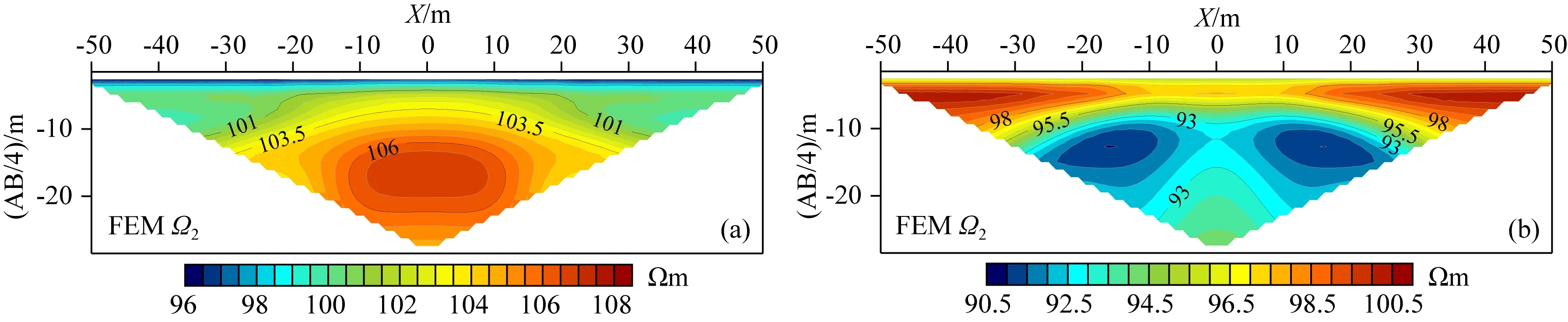
图14 不同电阻率异常体有限单元法采用计算域Ω2获得的视电阻率拟断面图(a) 高阻水平圆柱状异常体; (b) 低阻水平圆柱状异常体.Fig.14 The apparent resistivity of forward modeling results by using the FEM method with computational domain Ω2(a) Resistance anomaly; (b) Conductive anomaly.

图16 不同电阻率异常体FEM-MLS耦合法采用计算域Ω1模拟结果相对误差分布(a) 高阻水平圆柱状异常体; (b) 低阻水平圆柱状异常体.Fig.16 The relative errors of forward modeling results by using the FEM-MLS coupling method with computational domain Ω1(a) Resistance anomaly; (b) Conductive anomaly.
为了进一步研究FEM-MLS耦合法的模拟性能,采用范围更小的计算域对水平圆柱状异常体模型进行模拟.在计算域Ω1及其节点分布基础上,将计算域范围缩小为不同范围的计算域Ω3~Ω5(计算域按序号逐渐减小),计算域Ω3~Ω5分别如图12(c—e)所示.计算域Ω3:水平方向宽160 m(X:-80~80 m),垂直方向高60 m(Z:0~60 m)的,共11149个节点;计算域Ω4:水平方向宽140 m(X:-70~70 m),垂直方向高50 m(Z:0~50 m)的,共8519个节点;计算域Ω5:水平方向宽130 m(X:-65~65 m),垂直方向高40 m(Z:0~40 m)的,共6699个节点.利用FEM-MLS耦合法分别采用计算域Ω3~Ω5进行正演模拟,模拟结果如图17所示.对比分析图17和图14可知,FEM-MLS耦合法采用计算域Ω3~Ω5的模拟结果与参考结果基本相同.以参考结果(图14)为基础,计算FEM-MLS耦合法采用计算域Ω3~Ω5的模拟结果相对误差,相对误差分布如图18所示.

图17 FEM-MLS耦合法采用计算域Ω3~Ω5获得的视电阻率拟断面图(a) 高阻异常体; (b) 低阻异常体.Fig.17 The apparent resistivity of forward modeling results by using the FEM-MLS coupling method with different computational domains Ω3~Ω5(a) Resistance anomaly; (b) Conductive anomaly.

图18 FEM-MLS耦合法采用计算域Ω3~Ω5的模拟结果相对误差分布(a) 高阻异常体; (b) 低阻异常体.Fig.18 The relative errors of forward modeling results by using the FEM-MLS coupling method with different computational domains Ω3~Ω5(a) Resistance anomaly; (b) Conductive anomaly.
对比图18和图16可知,采用计算域Ω3~Ω5模拟时,水平圆柱状异常体为高阻和低阻的模拟结果相对误差均有所增加,并随着计算域范围的减小相对误差逐渐增大,其中异常体为高阻时增加较低阻异常体明显.表2列出了FEM-MLS耦合法采用计算域Ω3~Ω5时模拟结果的最大相对误差和平均相对误差,异常体为高阻或低阻时平均相对误差均很小,异常体为高阻时最大相对误差不超过0.4%,异常体为低阻时最大相对误差不超过0.2%,表明当计算域范围进一步减小时,FEM-MLS耦合法仍然能获得良好的模拟精度.以上分析进一步表明,在保证模拟精度前提下,有限单元法中采用无单元法计算边界积分,可有效地缩小计算域范围要求,相比于有限单元法,采用更小的计算域便可得到良好的模拟结果.

表2 FEM-MLS耦合法采用计算域Ω1,Ω3~Ω5模拟结果的相对误差Table 2 The relative errors (%) of simulation results by using the FEM-MLS coupling method with different computational domains: Ω1,Ω3~Ω5
缩小计算域范围要求不仅使得建模更加方便,同时也可减少节点和单元数量,提高计算效率.表3为不同方法和不同计算域单元数、节点数和计算时间(为对52根电极进行了电位正演模拟耗时).有限单元法采用计算域Ω2时,由于计算域Ω2在计算域Ω1基础上进行了扩边,使用了更多的节点和单元,因此增加了计算时间.FEM-MLS耦合法采用计算域Ω1计算不需要扩边处理,计算效率与采用计算域Ω1的有限单元法一致.FEM-MLS耦合法采用计算域Ω3~Ω5计算时,由于计算域范围更小,相比于计算域Ω1和Ω2,节点和单元数更少,因此计算量更少,有效提高了计算效率.结果表明,在计算精度(平均相对误差)基本一致的情况下,但本文算法采用较小范围的计算域,建模方便,使用更少的单元和节点,相比于采用较大计算域满足边界条件的有限单元法计算效率提高了约一倍.
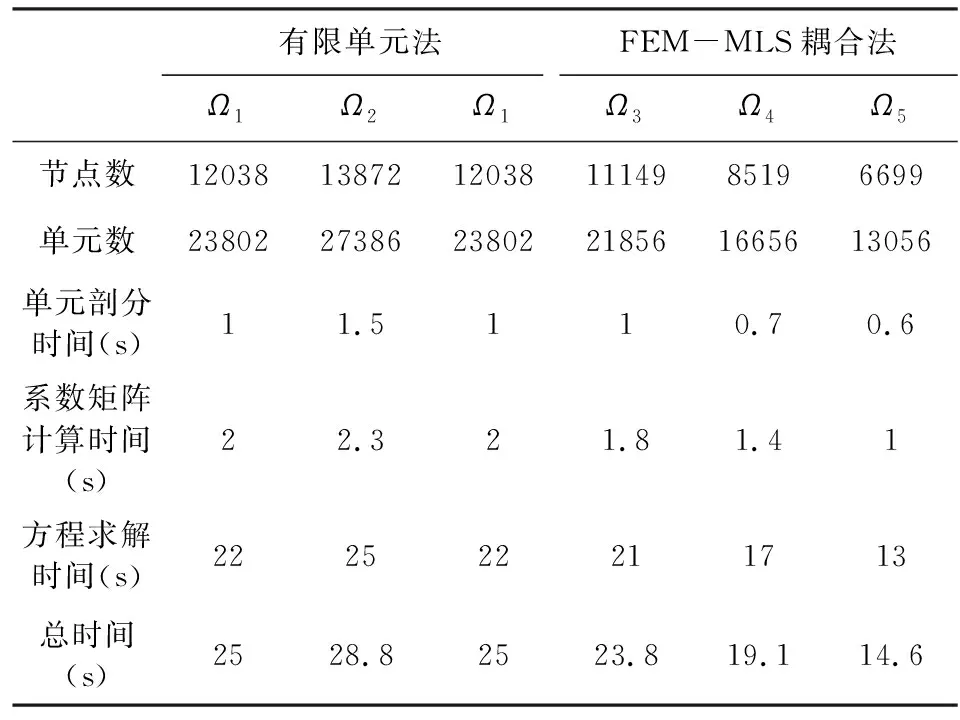
表3 不同方法和不同计算域节点数、单元数和计算时间Table 3 Number of nodes, number of cells and calculational cost of different methods using different computational domains
5 结论
本文提出一种具有高精度、高效的电阻率法有限单元-移动最小二乘(FEM-MLS)耦合正演算法,该算法将无单元法中的移动最小二乘(MLS)形函数应用于电阻率法有限单元正演的第三类边界条件处理.本文算例分析表明,采用第三类边界条件时,FEM-MLS耦合法可在较小范围计算域内获得良好的模拟精度,与有限单元法采用较大范围计算域的正演模拟效果相当,验证了本文算法的有效性.本文算法采用较小范围的计算域,建模方便,使用更少的单元和节点,相比于采用较大计算域满足边界条件的有限单元法计算效率提高了约一倍,相比于采用相同较小范围计算域的有限单元法平均精度提高了约一倍.通过数值模拟分析了FEM-MLS耦合法的参数选择对正演模拟的影响.分析表明,FEM-MLS耦合法中子边界上使用不同的高斯点数对模拟精度影响不大,不同高斯点支持域内节点数及其组合形式对模拟精度影响较大,需确保子边界两个端点对应的节点均包含于支持域内.基于对三层地电模型模拟结果分析,FEM-MLS耦合法在处理边界条件时,建议子边界上采用三角形单元的三个节点作为支持域构造MLS形函数,采用两个高斯点计算边界积分.
致谢感谢审稿人对完善本文提出的宝贵的具有建设性的意见和建议.在本文研究过程中,中南大学的刘海飞副教授、郭荣文研究员、崔益安教授、孙娅副教授及刘嵘特聘副教授给予了很多帮助和宝贵意见,在此表示感谢.
