引入非局部模块卷积神经网络的基频提取模型

刘晶晶，黄 浩

（新疆大学 信息科学与工程学院，乌鲁木齐 830017）

0 概述

基本频率或基音是语音信号的重要参数，在语音产生的数字模型中是激励源的一个重要参数。基频提取是一项从音频信号中估计最低频率部分的任务，近年来一直是一个流行的研究课题。准确检测语音信号中的基频周期对高质量的语音合成［1］、语音识别［2］、说话人识别［3］、语音增强［4］等各种语音应用起着至关重要的作用。

目前，研究人员已经提出了各种用于基频提取的方法。传统的基频提取方法包括简单的信号处理算法和启发式算法。现有的传统方法通常使用某个候选生成函数，通过预处理和后处理阶段来获得基频曲线。这些函数包括频谱［5］、自相关函数（Autocorrelation Function，ACF）［6］、平均幅度差函数（Average Magnitude Difference Function，AMDF）［7］、RAPT［8］和PRAAT［9］中的归一化互相关函数（Normalized Cross-Correlation Function，NCCF）以及YIN［10］。最近提出的传统方法包括PEFAC［11］、SWIPE［12］、pYIN［13］等。pYIN 是对YIN算法的改进，它使用概率模型从时域输入信号的累积平均归一化差函数来预测脉冲序列。PEFAC［11］算法使用匹配滤波器分析对数频域中的噪声信号，并使用通用长期平均语音频谱进行归一化，该归一化阶段使用基频提取滤波器来减弱强噪声分量，该基频估计滤波器可以忽略具有平滑功率谱的宽带噪声。SWIPE［12］将基频估计为匹配输入信号频谱的锯齿波形。除这种实时数字信号处理方法外，还开发出了使用隐马尔可夫模型（Hidden Markov Model，HMM）［14］、高斯混合模型（Gaussian Mixture Model，GMM）［15］、贝叶斯网络［16］等机器学习方法来进行鲁棒的基频提取。

目前的研究使用数据驱动的方法进行基频提取。其中应用深度神经网络（Deep Neural Network，DNN）及其变体，包括卷积神经网络和递归神经网络（Recurrent Neural Network，RNN）改善严重噪声条件下的基频提取。只要深度神经网络在其隐藏层中包含足够数量的单元，它们就会派生判别模型来表示任意复杂的映射函数。因此，相比较于传统方法，深度神经网路模型能够处理具有更强相关性、更高维度的输入特征。

文献［17］介绍了使用监督学习来提取基频，将基频的预测问题转换为分类问题，其中概率基频状态是直接从嘈杂的语音数据中学习的。该研究给定观测值的2个替代神经网络，它们模拟了基频状态分布：第1个是前馈深度神经网络，它在静态帧级声学特征上进行训练。第2 个是递归深度神经网络，它在连续的帧级特征上进行训练并能够学习时间动态。DNN 和RNN都产生基频状态的准确概率输出，然后通过维特比解码将其连接到基频轮廓中。该基频提取算法对不同的噪声条件具有鲁棒性，甚至可以应用于混响语音。但是，基频轮廓的最终估计值具有有限的频率分辨率，该分辨率由量化的频率状态数决定，就基频的估计精度而言，这是一个潜在的问题。文献［18］介绍了递归神经网络回归模型，该模型将频谱序列直接映射到基频值，以解决上述分类方法中的缺点。首先，该模型采用直接波形输入而不是频谱序列。其次，提出了一种新的基频信息的编码方法，即使用一个以基频的基本真值振荡的简单正弦波。这种编码使模型能够将原始语音波形映射到原始正弦曲线，而无需进行其他预处理或后处理。最后，也为实验增加了噪声条件，以便针对各种噪声类型检查噪声鲁棒性。

文献［19］介绍的CREPE 是一种直接在时域波形上运行的深度卷积神经网络（Convolutional Neural Network，CNN）的算法。该算法优于SWIPE［12］和pYIN［13］等启发式方法，同时对噪声也更加鲁棒。该网络结构存在以下不足：在该网络结构中，将每帧1 024 个音频样本点作为输入，全连接层在一层可以获取全局信息，但是它带来了很多参数，并且增加了网络优化的难度；全连接层还需要固定大小的输入和输出，并且会失去位置信息。这些缺点在许多情况下限制了全连接层的使用。文献［20］介绍的FCNF0 使用了全卷积网络（Fully Convolutional Network，FCN）结构。FCNF0使用等效的卷积层代替了最后的全连接层，该卷积层的长度等于输入矢量的时间维，并且卷积核的数量等于预期输出的大小。由于卷积层不需要固定大小的输入，因此此网络只允许在整个输入信号上运行一次卷积，而不是逐帧运行，从而节省了大量的计算量。然后，网络将不会输出单个矢量，而是会在每个时间步长包含输出预测矢量的三维矩阵。然而，上述使用几种卷积神经网络提取基频的方法没有考虑到相邻帧与帧之间的关系，而且也没有捕获远程全局的帧与帧之间的关系。这些问题会直接导致基频提取的性能下降。

为了解决卷积运算的上述问题，本文提出了使用带有非局部模块的卷积神经网络来进行基频提取。非局部模块计算所有音频样本点之间的相似性，即可以快速捕获长范围的帧与帧之间以及样本点与样本点之间的相互依赖关系，以较少增加计算复杂度来捕获音频的全局信息。

1 基于卷积神经网络的基线模型

本文使用了文献［19］介绍的基于卷积神经网络的基线模型CREPE，CREPE 是一种数据驱动的基频提取算法，该算法直接在时域波形上运行深度卷积神经网络。深度卷积神经网络的输入来自时域音频信号的1 024 个音频样本，经过6 个卷积层，产生2 048 维的潜在表示。然后将其与对应于360 维输出向量的S 型（Sigmoid）激活函数连接到输出层。

该网络结构存在以下缺点：在该网络结构中，使用的卷积核非常长（第1 层的输入是1 024 个音频样本），每层的大多数卷积运算都会导致与零的乘法运算，模型不会受益，反而会增加计算量。这与应用于每层卷积层的零填充（“same”卷积）有关，这是保持该层的输入和输出之间相同大小所必需的，并且由于CREPE 只能接受固定大小的输入，这意味着必须以帧为基础预测基频。同时，由于卷积神经网络提取基频的方法没有考虑到相邻帧与帧之间的关系，而且也没有捕获远程全局的帧与帧之间的关系。这些问题会直接导致基频提取的性能下降。

因此，本文首先提出使用带有非局部模块的卷积神经网络来进行基频提取。然后对网络的最后一层输出进行修改，将其对应于537 维的语音音频的输出。最后将修改后的模型应用于语音音频中的基频提取。

2 基频提取的非局部模块

2.1 非局部模块实例化

在文献［21］中，非局部操作根据输入的相似性聚合输入的信息，定义如下：

其中：i是要计算其响应的输出位置时间的索引；j是所有可能位置的索引；x表示输入信号；y是与x大小相同的输出信号；函数f(xi，xj)是用来计算i和所有可能关联的位置j之间的关系（相似度）；一元函数g(xj)是计算输入信号在位置j处的特征值；C(x)是归一化参数。为简单起见，仅考虑以线性嵌入的形式定义g函数，即：

其中：Wg是要学习的权重矩阵，通过1×1 卷积实现。

本文引入4 种计算相似性的f函数的形式：即高斯、嵌入式高斯、点积和级联。

2.1.1 高斯

f函数的自然选择是高斯函数，如式（3）所示：

其中：是点积相似度。

归一化因子C(x)表示为：

2.1.2 嵌入式高斯

高斯函数的扩展是计算嵌入空间中的相似度，如式（5）所示：

其中：θ(xi)=Wθ xi和ϕ(xj)=Wϕ xj是两个嵌入。最近提出的用于机器翻译的自注意力机制其实是非局部操作中嵌入式高斯函数的一个特例。

2.1.3 点积

f函数可以定义为点积相似度，如式（6）所示：

在这种情况下，将归一化因子设置为C(x)=N，其中N是x中的位置数，而不是f的总和，因为它简化了梯度的计算。

点积和嵌入式高斯之间的主要区别在于归一化指数函数softmax 的存在，它是一个激活函数，如式（7）所示，可被视为K个线性函数的softmax 函数的复合。

2.1.4 级联

f函数的级联形式如式（8）所示：

其中：[，]表示级联；Wf是一个权重向量，把级联的向量投影到一个标量上，将归一化因子设置为C(x)=N。在这种情况下，f函数中采用ReLU 激活函数，如式（9）所示：

2.2 非局部模块

非局部模块的输入和输出是具有相同数量的任意确定维度的特征。因此，非局部模块可以很容易地与其他深度神经网络模型相结合来构建网络模型。本文使用了二维卷积，其中将时间方向视为通道维度，卷积核执行帧与帧之间的卷积操作。非局部模块能够基于它们的相似性在远处的时频单元之间传递信息，因此可以应用于基频提取任务中来传递远距离样本点之间的信息。非局部模块中的残差连接定义如式（10）所示：

其中：yi通过式（1）给出；+xi表示残差连接。本文将非局部块插入卷积神经网络中，具有相同的输入输出维度，而不会破坏其初始行为（Wz初始为零）。一个非局部模块的内部结构如图1 所示。

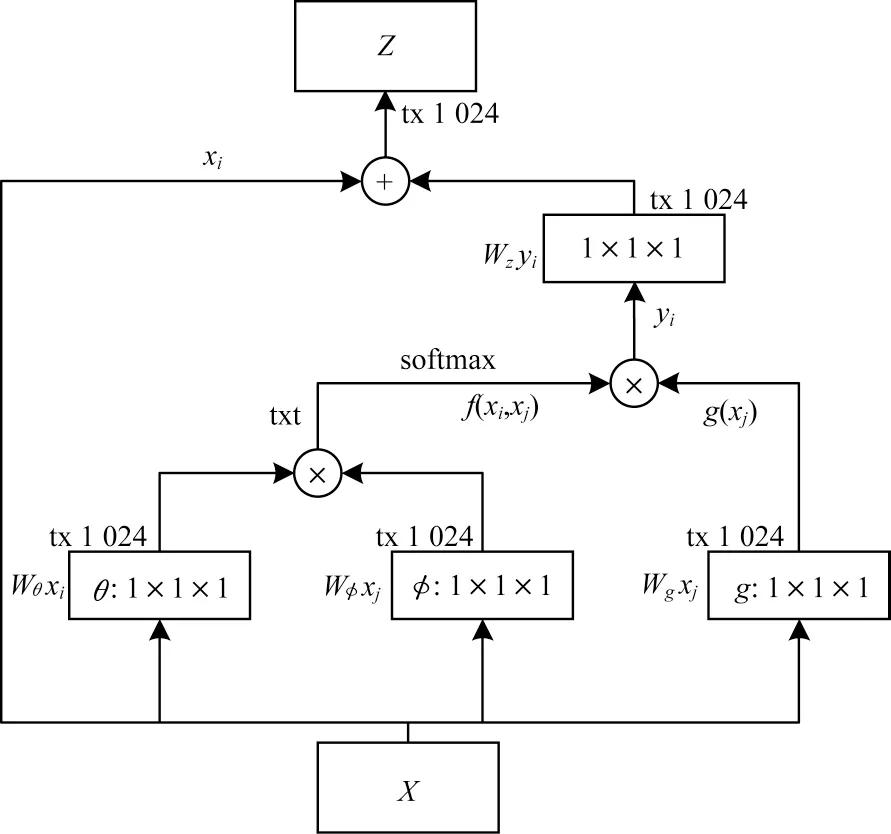
图1 非局部模块结构Fig.1 Non-local module structure

2.3 网络结构

图2 是一个用于基频提取的网络结构。网络的输入是时域音频信号的1 024 个音频样本点，本文使用多层卷积神经网络，其中一些卷积块与非局部模块相连。网络的前几层用于处理音频样本点的时域信息，并且可以将学习好的特征映射传递给后续的网络层。简单地增加非局部模块的个数并不能实现更好的性能。因此，本文将2 个非局部模块插入到卷积层的最后三层。最后使用一层具有线性激活的全连接层将前一层所获得的特征分为537 类，并得到每一帧音频的基频的后验概率。

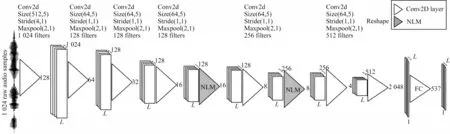
图2 网络结构Fig.2 Network structure

2.4 训练目标

为了使基频提取问题成为一个分类问题，将基频范围[fmin，fmax]量化为M个频点，这M个频点对应于 RAPT 中的M个基频状态。输出层的M个节点中的每一个都对应于区间的特定中心频率：

其中：Dp=0.005 是预定义的最小相对基频变化；fmax=500 Hz 是最大可能的基频值。本文通过在ci≥fmin中减小i来计算中心频率ci，其中fmin=50 Hz 是预定义的最小可能基频值。因此，最大状态数M=537。

如式（12）所示，训练网络是使用最小化目标向量y与预测向量之间的二元交叉熵：

其中：yi和都是0～1 之间的实数，表示模型的输出，yi表示每帧对应的基频的真实值。此损失函数使用文献［22］介绍的ADAM 优化器进行优化，学习率为0.000 5，训练了100 轮（epochs）。每个卷积层后面都有批归一化处理，后面是一个衰减层，衰减率为0.25。

3 实验设置

3.1 实验数据

实验数据集使用公开的基频语音数据库：格拉茨科技大学的基频跟踪数据库（PTDB-TUG）［23］，该数据库的文本内容来源于文献［24］介绍的TIMIT语料库，由2条方言句子（标记为sa）、450条语音紧凑的句子（标记为sx）和1 890条语音多样化的句子（标记为si）组成。表1所示为上述文本句子在PTDB-TUG数据集中与说话者之间的分布，其中：M 表示男性；F 表示女性。PTDB-TUG中包含来自20 位英语母语者的平行语料（10 位女性说话者，10 位男性说话者）。20 位说话者都阅读了2 条标记为sa 的句子。此外，每位说话者阅读了45 条标记为sx 的句子和189 条标记为si 的句子。音频总时长为9 h 36 min13 s，原始音频采样率设置为48 000 Hz，本文将其降采样至16 000 Hz，分别以80%、7%、13%进行训练、验证和测试。该语料库使用RAPT 算法提取基频的真实值。

表1 PTDB-TUG 数据库数据Table 1 Data of PTDB-TUG database

3.2 评价方法

根据以下评价指标评估基频提取结果：

1）平均绝对误差（Mean Absolute Error，MAE）。文献［25］介绍的MAE 表示预测值与真实值的所有绝对误差的平均值，MAE 是一种线性分数，所有个体差异在平均值上的权重都相等，如式（13）所示：

其中：N表示数据集中所有帧的总数表示模型的输出；yi表示每帧对应的基频真实值。

2）检测率（Detection Rate，DR）。在有声帧上评估DR，如果估计偏差在真实值的1%以内，则认为基频估计是正确的。

其中：N0.01表示正确估计的基频与真实值的偏差不超过1%的情况；Np表示有声帧的总数。

3）总基频误差（Gross Pitch Error，GPE）。文献［26］介绍的GPE 表示的是所有相对误差大于其基频真实值的20%的浊音帧。

其中：NGPE表示基频估计错误的帧数；Nv表示语音帧的总数。估计错误是指估计的基频与真实值的偏差超过20%的情况。

4 实验结果与分析

4.1 实验结果

本文首先确定加入网络中最优的非局部模块的数量。表2 所示为分别在训练集、验证集和测试集上具有不同数量的非局部模块的MAE。其中，f函数为嵌入式高斯形式。可以发现：当使用2 个非局部模块时已经给出最佳性能，在卷积神经网络中加入2 个以上的非局部模块并不能带来更好的效果。从实验结果可以看出：前几层的卷积神经网络已经可以学习一些局部特征，以便为后续其他网络层学习更好的特征。

表2 不同数量的非局部模块基频提取的MAE 结果Table 2 MAE results of fundamental frequency extract for different numbers of non-local modules

本文验证了4 种不同的f函数的形式对整个模型的影响。从表3 可以看出：使用嵌入式高斯模型性能最好，在测试集上其MAE 只有4.8，这也是文献［27］中介绍的自注意力机制的一种等价操作。当f函数为高斯时，在4 种f函数中性能最差，其在测试集上MAE 为5.2。相比于CREPE 基线模型，使用这4 种f函数中的任何一种，模型的性能都有提升，这也说明了本文在基线模型中加入非局部模块的合理性。

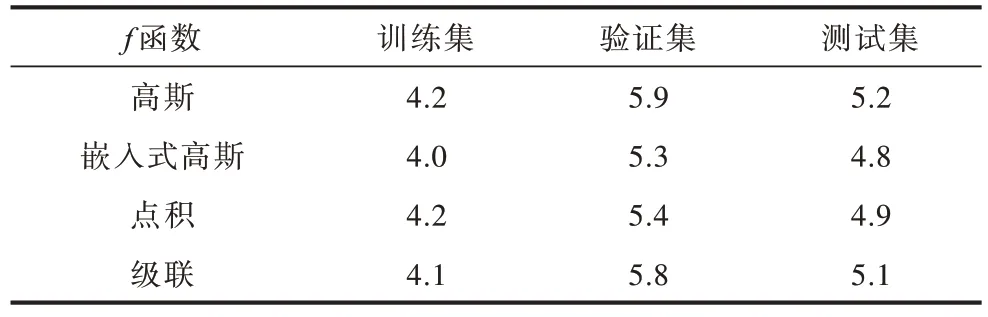
表3 使用2 个非局部模块的4 种不同f 函数形式的MAETable 3 MAE for four different f functional forms using two non-local modules

本文使用嵌入式高斯形式来验证拼接相邻几帧的信息对模型性能的影响。表4 所示为加入2 个NLM 后获取全局特征并且分别拼接5、7、9、15 帧获取局部特征的实验结果。可以看出：在测试集上拼接5 帧的MAE 最低，为4.7（本文后续的对比实验将使用该模型与基线模型对比），但是随着拼接帧数的增加，MAE 反而开始上升，模型性能在下降。当拼接的帧数在9 帧以上时，对整个模型的影响没有变化。这也验证了相邻几帧之间的信息对当前帧的基频值影响比较大，但随着时间变化，远距离音频帧之间的影响并不大。

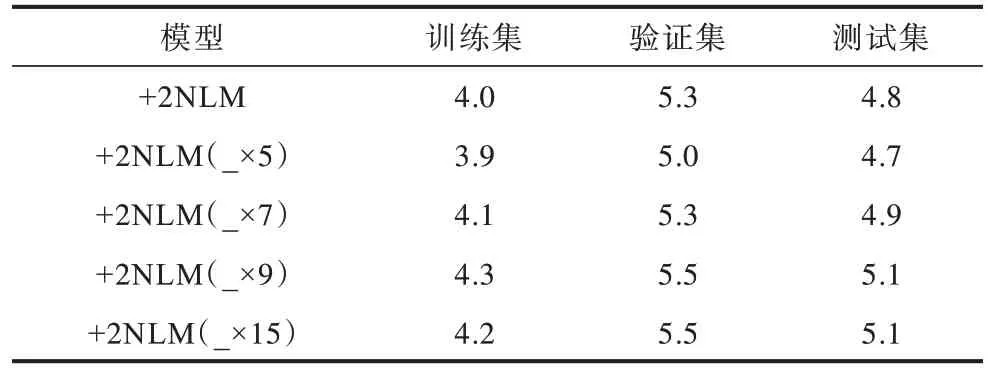
表4 拼接相邻几帧的MAE 结果Table 4 MAE results of splicing adjacent frames

4.2 对比实验

为了验证本文在基频提取任务中的有效性，本文选择了3 种基线模型：RAPT［8］，DNN［17］和CREPE［19］，调用了PyThon pysptk 库中的RAPT 算法。深度学习方法DNN 模型是一个从音频到量化频率状态的分类模型，它包括3 个隐藏层，每层有1 600 个Sigmoid 激活单元，以及1 个softmax 输出层，其大小设置为基频状态的数量。CREPE 其代码地址为：https：//github.com/marl/crepe。由于CREPE 模型是用于音乐基频提取，因此本文修改了模型最后的输出层，将特征分为537 类。

表5 所示为本文所提出的模型与RAPT、DNN和CREPE 模型的对比结果。可以看出：由于CREPE模型是音乐数据集上的基频提取模型，本文将其最后一层全连接层进行修改（其他层保持不变）应用到语音数据集上，所得到的MAE 为5.5。RAPT 模型由于是传统方法，没有用到现在流行的深度学习的模型，因此结果较差，MAE 高达7.8。基于 DNN 的方法利用帧级特征来计算基频状态的后验概率。虽然它利用相邻帧来合并时间信息，但由于特征维数的限制，无法捕捉长范围的依赖关系，因此使用该模型的结果相比于传统模型，MAE 提升了1.5 个百分点。但是相比于深度学习的CREPE 模型，DNN 模型并没有优势。而本文所提出的模型其MAE 达到了最佳，只有4.7。

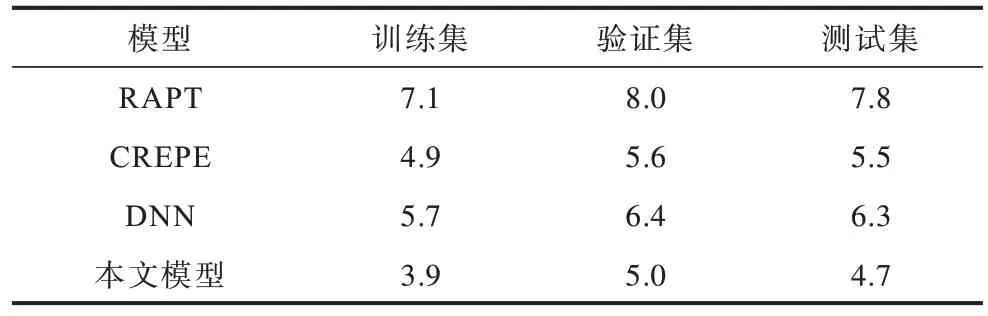
表5 不同模型的MAE 结果对比Table 5 Comparison of MAE results for different models

如表6 所示，在测试集上，本文所提出的模型的GPE 比传统模型RAPT 降低了2.5 个百分点。同时，本文模型在测试集上比基线模型CREPE 的GPE 降低了0.4 个百分点，这也证明了加入非局部模块后估计基频帧错误率会下降。

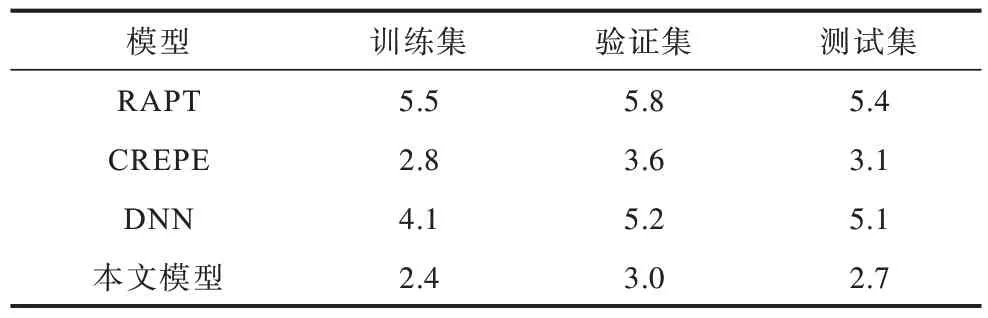
表6 不同模型的GPE 率结果对比Table 6 Comparison of GPE rate results for different models

不同模型的DR 如表7 所示，本文所提出的模型在测试集上的DR 为93.4%，而CREPE 的DR 为92.8%，这也表明了加入非局部模块后网络的整体性能有一定的提升。相比之下，基于DNN 的基频提取模型的性能较差，其DR 只有91.7%。

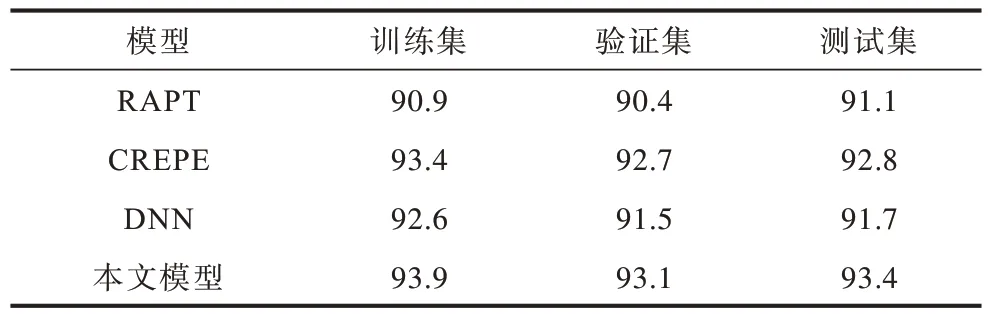
表7 不同模型DR 结果对比Table 7 Comparison of DR results for different models %

5 结束语

本文提出一种改进的基频提取模型，该模型非局部模块能够通过计算所有帧之间的相似度来捕获时域中的全局信息。非局部模块具有相同的输入输出，因此可以与任何现有的网络结构同时使用。在此基础上，验证了相邻几帧之间的信息对当前帧的基频值影响较大，但随着时间变化，远距离音频帧之间的影响并不大。实验结果表明，本文提出的网络比基线模型具有较好的性能，其在测试集上的MAE 只有4.7。然而，本文模型仍处于开发阶段，下一步将研究深度自注意力变化网络以及对基频提取有益的先验知识，进一步提升基频提取模型性能。