基于目标扰动的AdaBoost 算法
2023-03-16张淑芬董燕灵徐精诚王豪石
张淑芬,董燕灵,徐精诚,王豪石
(1.华北理工大学理学院,河北 唐山 063210;2.河北省数据科学与应用重点实验室,河北 唐山 063210;3.唐山市大数据安全与智能计算重点实验室,河北 唐山 063210;4.唐山市数据科学重点实验室,河北 唐山 063210)
0 引言
大数据时代下,海量数据以及强大的数据分析与数据挖掘能力无不反映了数据的高价值性,然而由于一些数据发布者缺乏管理和保护数据的意识,使攻击者有机可乘。虽然现有的隐私保护技术如数据脱敏[1]、k-匿名[2]、同态加密[3]等方法能在一定范围内保护数据中的隐私信息,但当攻击者拥有强大的背景知识时,同样无法抵抗攻击者的攻击。于是,差分隐私保护技术[4-6]应运而生。差分隐私保护技术不需要假设攻击者有背景知识,且成功地避免了攻击者会因为新样本的出现而得到新的知识。该技术允许数据收集者采用拉普拉斯机制[7]、指数机制[8]或高斯机制[9]对数据添加噪声进行扰动,从而使攻击者无法辨别某一样本是否在数据集中。
差分隐私通过添加噪声来扰动数据,使查询结果具有一定的随机性。主要的扰动方式有输入扰动、输出扰动和目标扰动。输入扰动对原始数据直接添加噪声,扰动后的数据成为模型学习的输入,直接参与之后的训练。输出扰动是指对模型的最终输出添加噪声,得到扰动后的结果。目标扰动通过对目标函数添加噪声,使最终模型的输出具有随机性。
当前,随机森林[10-18]是将差分隐私应用于集成学习中的主要研究方向,然而将差分隐私与AdaBoost 算法结合的研究却甚少。这是因为差分隐私AdaBoost 算法面对的挑战[19]主要是算法迭代引起的噪声叠加造成最后模型无法收敛和分类准确率较低。Gambs 等[20]提出了2 种隐私保护AdaBoost算法,适用于2 个或2 个以上参与者在不直接交流数据集的情况下保护参与者的数据隐私。Li 等[21]选取AdaBoost 算法作为每个参与者的本地学习器,提出一种基于集成策略的自适应分布式隐私保护数据挖掘技术。沈思倩[22]分别研究了基于完全数据集和不完全数据集的差分隐私Adabooot 算法。贾俊杰等[23]进一步将分类与回归树(CART)取代树桩作为AdaBoost 算法的基分类树。但上述研究都只是对弱学习器的类标签或类计数进行了加噪,而且在敏感度的计算上也不够严谨。Li 等[24]首次将梯度提升决策树与差分隐私相结合,在敏感度的计算上更加精确。在这些已有的将差分隐私与AdaBoost算法结合的研究中,主要有3 个缺陷:一是隐私预算的分配不具有针对性,较泛化;二是在敏感度的计算上不够严谨;三是在添加噪声上,尚未解决AdaBoost 算法由于多轮迭代而放大噪声的问题。为此,本文提出对每轮迭代过程中的最大最小样本权值进行加噪,针对该加噪对象提出一种动态的隐私预算分配策略,严谨地根据敏感度定义计算了查询函数最大变化范围,并提出了3 种能有效控制噪声叠加过大并提高模型可用性的方案。实现在保护数据的同时让模型拥有更高的分类准确率。具体来说,本文的主要工作如下。
1) 提出了一种基于目标扰动的AdaBoost 算法。根据AdaBoost 的目标函数,提出本文实现AdaBoost 差分隐私保护的加噪时机。
2) 针对AdaBoost 算法每轮迭代的样本权值分布,选取最具代表性的最大权值和最小权值,并通过动态的隐私预算分配策略分配不同的隐私预算。
3) 根据敏感度定义,准确计算最大权值和最小权值的动态敏感度。
4) 为有效解决因每轮迭代加噪而引起的分类准确率失真、模型不可用问题,提出基于摆动数列、随机响应和改进的随机响应3 种噪声注入方案,并在真实数据集上进行实验,以评估不同算法的有效性。
1 差分隐私保护技术
差分隐私保护技术最早被应用于数据库安全领域,查询2 个仅相差一条记录的数据集,发现得到相同结果的概率非常接近,使攻击者无法进行差分攻击。
1.1 差分隐私的定义及相关概念
设数据集D与具有相同属性结构的数据集D′的对称差为DΔD′,|DΔD′|表示DΔD′中记录的数量。若|DΔD′|= 1,则称D和D′为邻近数据集。
定义1差分隐私[4-6]。设有随机算法M,PM为M所有可能的输出构成的集合。对于任意2 个邻近数据集D和D′以及PM 的任何子集SM,若算法M满足
则称算法M提供ε-差分隐私保护,其中,参数ε为隐私预算,表示数据集中增加或减少一条记录时,算法M的输出结果一致的概率;Pr[·] 表示发生某一事件的概率。
定义2全局敏感度[7]。对于2 个邻近数据集D和D′,查询函数f最大的变化范围为全局敏感度Δf,则Δf的计算式为
定义3串行组合[7]。差分隐私具有灵活的组合特性。假设有n个随机算法K,其中Ki满足εi-差分隐私,那么对于同一数据集,由{Ki(}1 ≤i≤n)组合后的算法满足sum(εi)-差分隐私。
1.2 实现机制
拉普拉斯机制通过向查询结果中添加随机噪声来实现差分隐私保护,并且添加的随机噪声是服从拉普拉斯分布的。设尺度参数为λ,位置参数μ=0,则该拉普拉斯分布为Lap(λ),它的概率密度函数为
不同尺度参数 的拉普拉斯分布如图1 所示。

图1 不同尺度参数λ 的拉普拉斯分布
定义4拉普拉斯机制[7]。给定数据集D和隐私预算ε,设有查询函数f(D),其敏感度为Δf,那么随机算法M(D) =f(D)+Y提供ε-差分隐私保护。其中,为随机噪声,并服从尺度参数为的拉普拉斯分布。拉普拉斯机制的整体思想是以一定的概率输出异常值。为了使加噪后的数据脱离真实值,需要提高输出异常值的概率,即稳定地得到一个异常值,因此当拉普拉斯函数曲线越平缓时,异常值输出的概率就越高,数据相对于正确的中心值更加分散。
2 AdaBoost 算法
AdaBoost[25-27]是前向分步加法算法的特例,通过迭代,将前一轮强学习器的学习结果与当前一轮弱学习器的学习结果加权,来更新当前的强学习器。在训练弱学习器时,减小上一轮样本被正确分类的样本权值,提高样本被错误分类的样本权值。在最终加权组合成强学习器时,加大分类误差率小的弱学习器的权重,减小分类误差率大的弱学习器的权重。
本文使用的主要符号如表1 所示。
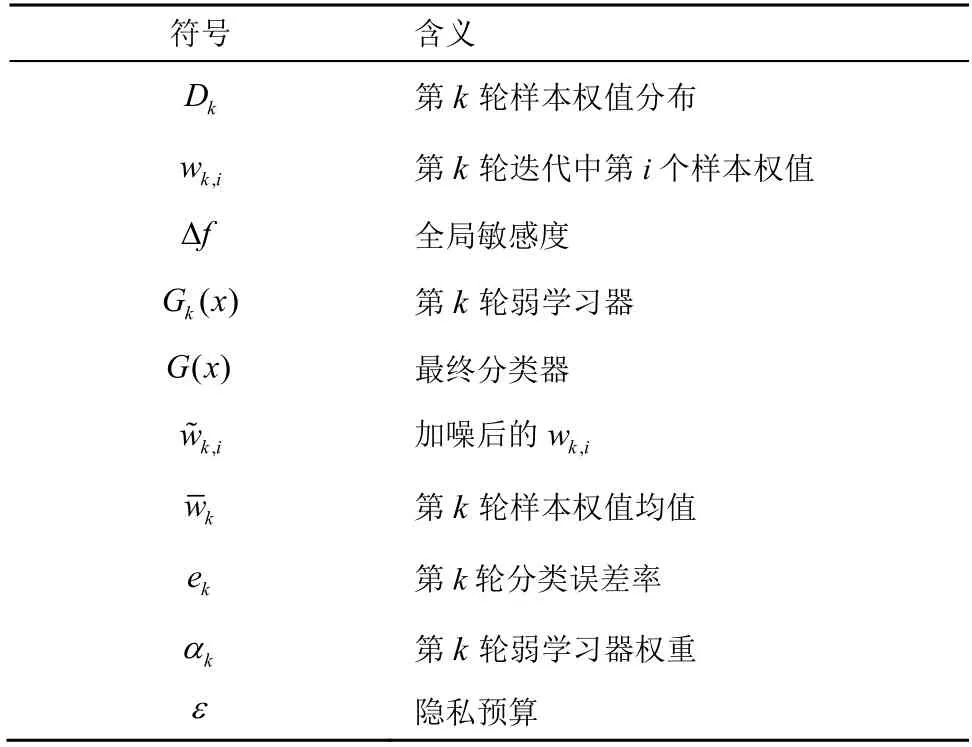
表1 主要符号
2.1 AdaBoost 目标函数
AdaBoost 算法的损失函数为指数函数[28],即定义损失函数为
将损失函数代入目标函数中,则AdaBoost 的目标函数为
由于AdaBoost 算法是前向分步算法,假设第k轮的强学习器为f k(x),第k-1轮的强学习器为f k-1(x),第k轮的弱学习器为Gk(x),则有以下关系
AdaBoost 的目标是使前向分步算法得到的αk和Gk(x)能让f k(x)在训练集上的指数损失最小,即AdaBoost 的目标是最小化目标函数,表示为
2.2 AdaBoost 算法流程
算法1AdaBoost 算法
输入训练集T,迭代次数m
输出最终分类器G(x)
3 AdaBoost 算法的隐私保护
在AdaBoost 算法的实际应用过程中,算法模型会在生命周期的各个阶段面临不同的安全威胁,导致模型的隐私信息被泄露,模型的可用性、完整性被破坏。为了减少此类现象的发生,需要对AdaBoost 算法进行隐私保护。
从隐私保护的角度来看,根据注入噪声的时机,实现差分隐私有输入扰动、输出扰动和目标扰动这3 种方法。本文选取目标扰动作为AdaBoost算法实现差分隐私保护的加噪时机,并根据2.1 节AdaBoost 目标函数,取样本权值作为加噪对象。
3.1 基于样本权值的动态隐私预算分配策略
在k轮迭代后,更新的样本权值wk+1,i成为下一次迭代中计算错分样本率的输入。由于每一轮迭代过程中,权值小的样本是前一轮被正确分类的样本,前一轮被错分的样本在下一轮中会被赋予更高的权值来加以重视。同时,为了能够实现AdaBoost算法的快速收敛,在添加差分隐私保护时,需对权值较大的样本分配多的隐私预算,对权值较小的样本分配较少的隐私预算。基于此,提出一种基于样本权值的动态隐私预算分配策略。
假设总的隐私预算为B,迭代次数为m,样本数为N,对于第k轮更新后的权值分布Dk+1,寻找出最大权值和最小权值,分别为最大权值和最小权值添加噪声。其中样本的初始权值不需要添加噪声,即。
此时,全局敏感度Δf是动态变化的,根据定义2,计算最大权值的全局敏感度Δf为
算法2隐私预算分配算法DPweight_dynamic
输入更新后的权值wk+1,i,迭代次数m,隐私预算B
输出样本权值
将DPweight_dynamic 算法与AdaBoost 算法结合,得到DPAda 算法。
算法3DPAda 算法
输入训练集T,迭代次数m,隐私预算B
输出最终分类器G(x)
3.2 迭代过程中的噪声控制
若对每轮最大权值或最小权值wk+1,i都添加噪声,则在多轮迭代后,当前的噪声会叠加到后续的分类器构造中,累加后的噪声会极大程度地影响最终分类器结果的质量。
此外,AdaBoost 算法在第一轮迭代后,权值分布两极化,即只有最大权值和最小权值。在对最大权值和最小权值添加2 种不同的噪声时,由于拉普拉斯噪声是随机的,且有正有负,就可能造成最大权值添加了负噪声,最小权值添加了正噪声。但由于最小权值在添加了正噪声后不可能超过权值均值,最大权值在添加了负噪声后不可能小于权值均值,因此就会出现最小权值或最大权值变为均值的情况。为避免这种极端情况的发生,在后文的算法中均从第二轮开始加噪。
3.2.1 基于摆动数列的噪声注入
定义5摆动数列[29]。一个数列从第2 项起,有些项大于它的前一项,有些项小于它的前一项,这样的数列叫做摆动数列。通过寻找摆动的平衡位置与摆动的振幅,可以得到摆动数列的通项公式。
假设有数列a,b,a,b,…,则该数列的平衡位置为,振幅为,通过(-1)n或 (-1)n+1调节,则该数列的通项为
本文选取a= 0,b=1的摆动数列,根据摆动数列第n项的值,判断是否为AdaBoost 算法的第n轮添加噪声。此时该数列的通项为
将基于摆动数列的噪声注入与DPAda 算法结合,得到DPAda_Swing 算法。
算法4DPAda_Swing 生成算法
研究证明HPV的感染是可以预防的,并且宫颈癌可能成为第一个可以用疫苗预防的癌症。研究发现,HPV的L1蛋白保守度高,因此可以作为HPV的特异性抗原用来研究制造病毒预防疫苗。目前市面上的预防疫苗都是利用重组的DNA分子所表达的病毒样颗粒(virus-like particles, VLPs)制成的疫苗。
3.2.2 基于随机响应的噪声注入
由于摆动数列稳定地、间隔性地输出相同值,不具有随机性,因此本文提出基于随机响应的噪声注入。
定义6随机响应。一随机实验在同样的条件下重复并相互独立地进行,该随机实验只有2 种可能结果:结果a和结果b。随机数x在(a,b)上服从均匀分布,即x~ U(a,b),,给定以下规则
则称h(x)满足随机响应,即随机实验满足随机响应。
本文在AdaBoost 算法的每轮迭代过程中,生成一随机数x,其中x服从a=0,b=1标准均匀分布,即x~ U(0,1),E(x)=0.5,则每轮迭代hk(x)满足随机响应
根据随机响应第k轮迭代输出的值,判断是否为AdaBoost 算法的第k轮添加噪声。
将基于随机响应的噪声注入与DPAda 算法结合,得到DPAda_Random 算法。
算法5DPAda_Random 生成算法
3.2.3 基于改进的随机响应的噪声注入
由于随机响应在每轮迭代中较随机地生成a和b,即可能出现连续几轮的输出值都为a或b,因此,本文提出了一种改进的随机响应。根据第k轮迭代输出的值,判断是否为AdaBoost 算法的第k轮添加噪声。
定义7改进的随机响应。若第i次迭代的输出值hi(x)=a,第i+1次迭代的输出值hi+1(x)=b,且第i+2次~第j-1次迭代中(j>i+2),每次输出值hk(x)均为b,直至第j次迭代的输出值h j(x)=a,则将第i+2次~第j-1次迭代的输出值hk(x)全置a。
取a= 0,b=1,将基于改进的随机响应的噪声注入与DPAda 算法结合,得到DPAda_Improved 算法。
算法6DPAda_Improved 生成算法
3.3 算法分析
3.3.1 加噪轮数分析
定理1令R为算法累计添加噪声的轮数,则。
证明DPAda 算法具有从第二轮起每轮都添加拉普拉斯噪声的特点,则
摆动数列可以稳定地输出 0101…,则DPAda_Swing 算法具有间隔性添加拉普拉斯噪声的特点,因此
随机响应在输出0 与1 时太过随机,因此,DPAda_Random 具有连续加噪或连续不加噪的特点,假设DPAda_Random 算法添加拉普拉斯噪声共s次,则
改进的随机响应有效规避了随机响应连续几轮加噪或不加噪的缺点,且具有间隔随机轮次加噪的优点,因此假设DPAda_Improved 算法添加拉普拉斯噪声共t次,则
因此可得
证毕。
3.3.2 算法时间复杂度分析
DPAda、DPAda_Swing、DPAda_Random 和DPAda_Improved 算法的时间复杂度估计为
其中,m为迭代次数,d为训练集中属性数量,n为训练集中样本个数。
3.3.3 算法隐私性分析
假设共有m轮迭代,对于第k轮迭代后更新的样本权值为最大权值的个数,为最小权值的个数。
定理2DPAda、DPAda_Swing、DPAda_Random和DPAda_Improved 算法满足B-差分隐私。
由定义3 差分隐私的串行组合性质可知
因此,DPAda、DPAda_Swing、DPAda_Random和DPAda_Improved 算法满足B-差分隐私。证毕。
4 实验及分析
4.1 实验数据
实验所选数据集来源于公开的UCI 机器学习数据库中的Adult 数据集和Bank Marketing 数据集,如表2 所示。
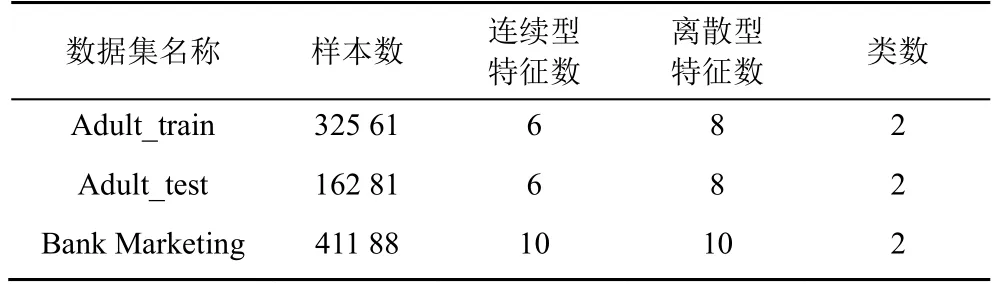
表2 实验数据集信息
通过对Adult 数据集的属性集进行分析发现,属性native-country 为非美国籍的样本数仅占总样本数的16%,因此本文实验仅选取美国籍的样本记录进行训练、测试。此外,属性fnlwgt 的值是通过对和当前样本具有相似人口特征的人进行加权统计而得出的人口总数,该属性对本文的实验结果无帮助,因此将它删除。本文选取Adult_train 作为训练集,Adult_test 作为测试集,选取Bank Marketing数据集的70%作为训练集,30%作为测试集。
4.2 实验结果与分析
在相同参数下,每组实验重复运行50 次取平均值来计算算法的平均分类准确率。x轴为总的隐私预算ε=B,y轴为算法平均分类准确率,其中B= 0.1,0.3,0.5,0.7,0.9,1.0,3.0,5.0,迭代次数m= 30,50,70,90,100。
图2 和图3 分别是不同数据集下DPAda_Swing算法、DPAda_Random 算法与DPAda_Improved 算法在不同迭代次数下的平均分类准确率对比。观察图2和图 3 不难发现,DPAda_Swing 算法与DPAda_Improved 算法的分类准确率虽偶有波动,但整体趋势基本随着ε的增加而增长,而DPAda_Random 算法的平均分类准确率波动很大,且当迭代次数m较小时,波动特别明显。这是因为DPAda_Random 算法在给样本权值wk+1,i添加噪声时,根据随机响应的输出特点,在输出0 与1 时太过随机,即可能连续几次迭代的输出值都为1,从而连续加噪,因此无法有效控制是否对第k轮迭代进行加噪。m越小,越难克服随机性带来的影响,当m较大时,可以通过多轮迭代来减少随机性带来的影响。DPAda_Swing 算法能够根据摆动数列稳定的输出值0101…,来间隔性地添加噪声。对于DPAda_Improved算法,虽然在输出0 与1 时仍具有随机性,但根据定义7,相较于DPAda_Random 算法中的随机响应,DPAda_Improved 算法使用改进的随机响应,有效减少了添加噪声的次数,达到了小于或等于DPAda_Swing算法中基于摆动数列添加噪声的轮数。观察图2(a)和图3(c)、图3(a)和图3(c)可以看出,在不同迭代次数m下,DPAda_Improved算法的分类准确率均高于DPAda_Swing 算法。
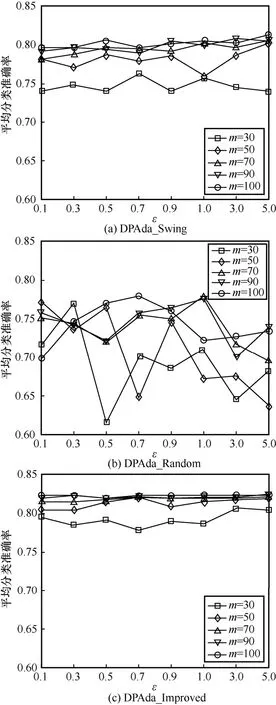
图2 Adult 数据集下3 种算法的平均分类准确率
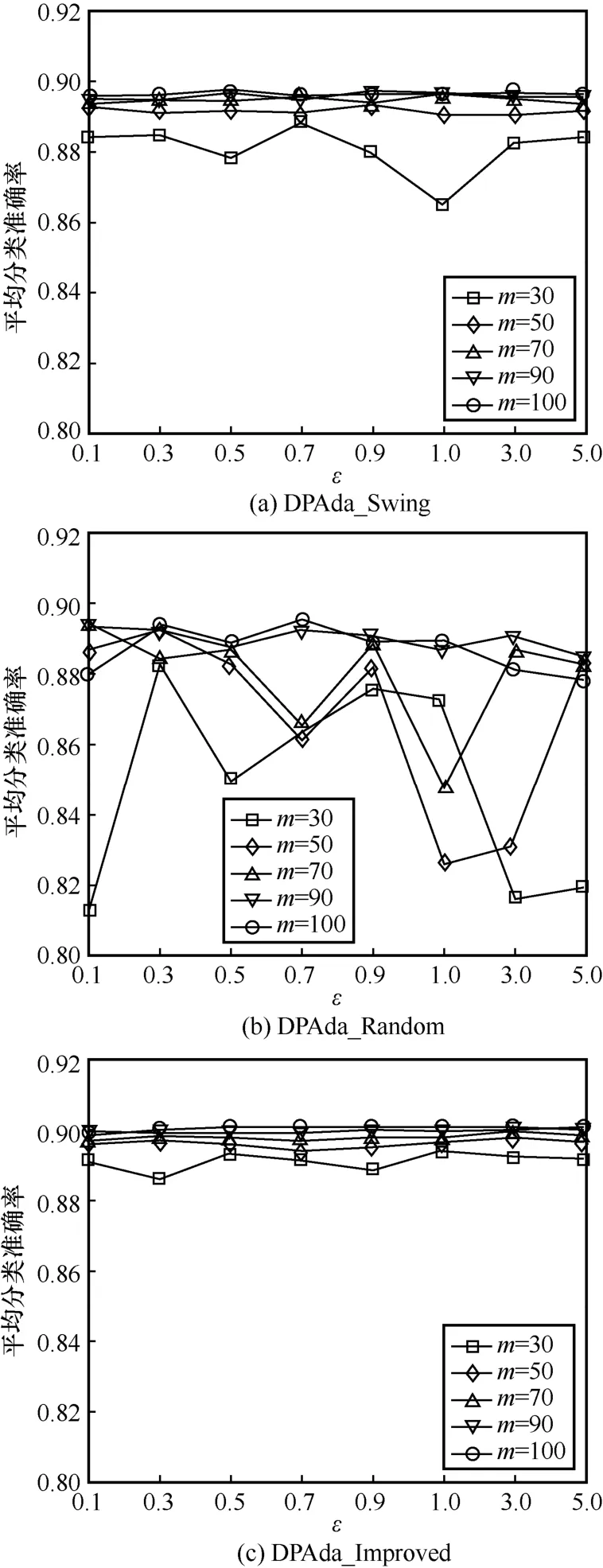
图3 Bank Marketing 数据集下3 种算法的平均分类准确率
本文还设置了在m= 50,70,90和ε=0.1,0.3,0.5,0.7,0.9,1.0,3.0,5.0 条件下,将不结合差分隐私的AdaBoost 算法、给类标签添加差分隐私保护的DP-AdaBoost 算法[22]、给CART 树的内部节点和叶子节点添加差分隐私保护的CART-DPsAdaBoost 算法[30]、从第二轮起每轮添加差分隐私保护的DPAda算法与本文提出的DPAda_Swing、DPAda_Random、DPAda_Improved 算法进行比较,实验结果如图4~图6 所示。

图4 m=50 时不同算法平均分类准确率

图5 m=70 时不同算法平均分类准确率
从图4~图6 可以看出,DPAda 算法的分类准确率很低,并随着迭代次数m的增加大体上呈下降趋势。这是由于DPAda 算法除第一轮迭代外,对之后每轮迭代都连续加噪。因此,在迭代次数m增加时,噪声便会随着迭代数的增加而叠加,最后使DPAda 算法的分类准确率不增反降。当m一定时,DP-AdaBoost、CART-DPsAdaBoost、DPAda_Swing 和DPAda_Improved 算法的分类准确率都随着ε的增加而增加;但当ε一定时,只有DP-AdaBoost 算法的分类准确率随着m的增加而下降。这是因为DP-AdaBoost 算法[22]添加噪声的对象为弱学习器的类标签,它并没有参与迭代过程,因此当ε一定时,随着迭代次数m的增加,弱学习器越多,分配到每一轮迭代的隐私预算减小,加噪就越明显,分类准确率就越低。CART-DPsAdaBoost 算法[30]是在形成CART 基分类器的过程中,对CART 的叶子节点和内部节点进行加噪,当基分类器个数增加时,噪声对构造最终分类器的影响逐渐减小。因此,随着m的增加,分类准确率逐渐提升;而DPAda_Swing 和DPAda_Improved 算法中添加噪声的对象为样本权值,且结合的是动态隐私预算分配策略DPweight_dynamic,该策略只对最大样本权值和最小样本权值加噪,保证了在添加噪声的过程中,最大样本权值在加噪后不会小于样本权值均值,最小样本权值在加噪后不会大于样本权值均值,因此仍能保证样本权值的主要分布。此外,DPAda_Swing 和DPAda_Improved 算法根据摆动数列和改进的随机响应,有效控制了加噪过程为非连续加噪,给予了弱学习器矫正收敛的机会,因此DPAda_Swing 和DPAda_Improved 算法的分类准确率随着迭代次数m的增加而增加。
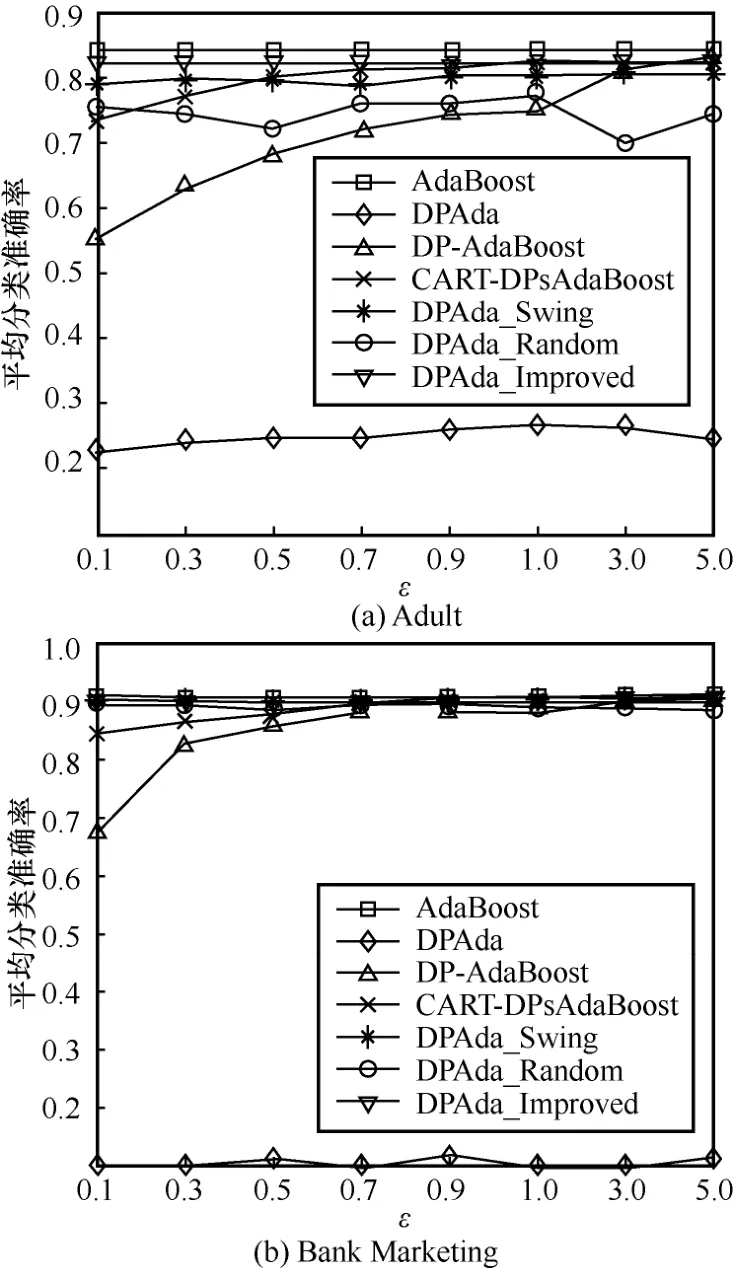
图6 m=90 时不同算法平均分类准确率
通过观察图4~图6 也不难看出,在不同迭代次数m和隐私预算ε下,在所有对比算法中,DPAda_Improved 算法在分类结果上表现得最稳定,分类准确率最接近不添加噪声的AdaBoost算法,实现了在保护隐私的同时,仍拥有更高的分类准确率。
综上,DPAda_Improved 算法与对弱学习器类标签添加噪声的DP-AdaBoost 算法[22]相比,不会有随着迭代次数的增加准确率反而下降的问题;在分类准确率的整体表现上,优于给CART 树添加噪声的CART-DPsAdaBoost 算法[30];有效解决了DPAda 算法由于连续加噪带来的噪声不断叠加、精确度极低、模型无法收敛导致模型不可用的问题;不仅在分类准确率上表现得比其他算法要好,还保留了DPAda_Random 算法的随机轮次加噪的特点,并有效地减少了随机性带来的影响,达到了小于或等于基于摆动数列的DPAda_Swing算法中添加噪声的轮数。最后,DPAda_Improved算法很好地做到了隐私保护与数据效用的均衡。
5 结束语
本文提出了一种基于目标扰动的差分隐私AdaBoost 算法,与现有的差分隐私AdaBoost 算法相比,本文算法的贡献如下。1) 选择了迭代过程中每个样本的样本权值作为添加差分隐私保护的对象,解决了在AdaBoost 算法多轮迭代过程中加噪的主要问题,即算法迭代带来的噪声叠加导致最终无法收敛,模型不可用,准确率极低的问题。2) 设计了一种动态的隐私预算分配策略。3) 给出了严谨的敏感度计算。4) 提出了3 种有效控制噪声叠加过多的算法,并通过实验证明了相较于 DPAda_Random 算法和DPAda_Swing 算法,DPAda_Improved 算法在拥有更高的分类准确率的同时,仍能实现数据的隐私保护。下一步,笔者将考虑把差分隐私应用于其他集成学习算法。
