基于局部传播中心性的影响力最大化算法

方 辉 姜久雷 李盛庆 李卫民

1(北方民族大学计算机科学与工程学院 宁夏 银川 750021) 2(常熟理工学院计算机科学与工程学院 江苏 苏州 215500) 3(上海大学计算机工程与科学学院 上海 200444)

0 引 言

在社交网络中,用户可以通过共享新闻、图片、视频和产品促销等信息来进行互动并建立联系[1]。于是,越来越多的企业开始选择在社交网络中进行产品营销,让产品信息通过社交网络传播得更广。例如,一家公司开发一个新产品,考虑到预算有限,该公司决定在产品销售初期选择一些有影响力的用户免费试用该产品,并希望这些用户会喜欢该产品,然后这些用户会推荐新产品给他们的朋友,而那些受影响的朋友很可能会影响他们的朋友。最终,该公司就可以拥有许多潜在客户。从形式上来讲,上述情况就称为“影响力最大化”问题,即在大规模社交网络中挖掘一个较小的节点集合,使得该集合在社交网络的影响范围更大。

在社交网络中,经典的影响力的度量方法有DegreeCentrality、EigenvectorCemtrality、K-shell和ClosenessCentrality[2-5]等。除此之外,Chen等[6]利用节点的邻居和下一个最近的邻居提出LC(Local Centrality)度量节点的影响力。Gao等[7]在LC的基础上,加入聚类系数提出LSC(Local Structure Centrality)度量节点影响力。Yang等[8]综合考虑节点度和两跳邻居的聚类系数,通过熵计算度和聚类系数所占权重,提出DCC度量节点的影响力。实验结果表明,LC、LSC和DCC更能区分不同节点的影响力。本文针对上述度量方法未考虑传播概率对节点扩展能力的影响,提出一种LPC度量方法。

影响力最大化问题首先是由Domingos等[9]提出的,并将其定义为一个算法问题。Kempe等[10-11]形式化地表示了影响力最大化问题,然后提出了影响范围达到为1-1/e(63%)的贪心爬山算法对该问题进行求解,并证明了影响力最大化问题是NP-hard问题。利用贪心算法求解需要运用多次蒙特卡罗(Monte-Carlo)模拟,导致算法非常耗时。为了减少算法的运行时间,许多学者提出了启发式算法。Chen等[12]提出DegreeDiscount算法,该算法的基本思想是当一个节点有邻居节点被选为种子节点时,在计算它的度数时要减少,其性能优于Degree算法[10]。Deng等[13]在IC模型的基础上,利用节点的中心性计算网络中每条边的传播概率,提出了基于中心性的独立级联模(Centrality-Based Independent Cascade Model, CIC),在DegreeDiscount[12]算法基础上提出NewDiscount算法,实验结果表明,NewDiscount算法比DegreeDiscount算法影响范围更广。Kundu等[14]基于传播概率和度中心性提出了基于传播度(diffusion degree)的启发式算法。因为该算法考虑到了节点间传播概率的影响,从而提高了算法的准确性。Li等[15]提出了三跳速度衰减传播模型(The three hops velocity attenuation propagation model),通过该模型为每个节点构造一个三跳传播路径,并提出了IMMRA,实验结果表明,该算法的影响范围与贪心算法十分接近,且运行时间有很大提升。Dey等[16]通过5种不同的中心性度量方法选择用于信息传播的种子节点,通过在不同数据集中使用Susceptible-Infected-Recovered(SIR)和Breadth First Search(BFS)模拟信息传播,最终通过比较受种子节点影响的节点数量发现,特征向量中心性优于其他中心性度量。但是考虑到特征向量中心性时间复杂度高,作者利用k-core将原始网络退化为较小的网络,然后选择种子节点,进一步减少了算法的运行时间。

对于影响力最大化问题,基于贪心策略能保证算法的精度较高但算法时间复杂度高,而启发式算法时间复杂度低但影响范围不如贪心算法。针对该问题,本文提出一种时间复杂度低且影响范围更大的IMLPC。

1 影响力最大化与传播模型

1.1 问题定义

在本文中,将社交网络建模为图,给定一个图G(V,E),其中:V表示节点集合;E表示边集。∀v∈V表示节点,∀e(u,v)∈E表示一条u指向v的边。

影响力最大化问题的目的就是找到有k个节点的种子集S(S=|k|),且S⊆V,使得在某种信息传播模型下被S影响的节点的预期数量σ(S)最大化。即选择k个可以使σ(S)达到最大值的种子节点。其表示如下：

(1)

式中：S*是选择的初始种子集合。

1.2 传播模型

本文采用独立级联(Independent Cascade, IC)模型模拟影响力的传播过程。在IC模型中,为每条边e(u,v)∈E指定了传播概率puv∈[0,1],这是u通过边影响v的概率。

给定网络图G(V,E)和种子集S⊆V,IC模型中节点有两种状态,即激活状态和未激活状态。IC模型传播过程如下。令S0=S,首先,S0中的所有节点都处于激活状态,而其他节点则处于未激活状态。在每个时间t,每个节点u∈St-1都有且仅有一次机会以传播概率puv影响其每个处于未激活状态的邻居v。如果v受影响,则将其添加到St并使v处于激活状态。当St为空时,该过程结束。令AS(S)表示最终受S影响的输出节点数目。因此,σ(S)表示如下：

(2)

式中：S是最初选择的种子集；ASi(S)是第i次传播过程中影响的节点数目;R是IC模型的模拟次数。

2 算法实现

2.1 局部传播中心性

在社会学文献中,度和其他基于度中心性的启发式算法通常用于评估社交网络中节点的影响力[1,17]。节点的度也常被作为影响力最大化问题中种子节点的选择依据。尽管选择最大度数的节点作为种子会有更大的影响力扩散,但却未考虑到种子节点的实际传播过程[14]。假设网络中具有最大度数的节点V1与一些度数较小的节点相连,而另一个度数较小的节点V2与一些度数较大的节点相连。在这种情况下,我们就不能单纯地选择V1作为种子节点,因为与V1的邻居相比,V2的邻居可以将信息发送给网络中更多的节点,V1在信息传播过程中影响范围反而更小。这是因为未考虑节点邻域的影响。

因此本文引入传播概率来量化节点的实际传播过程,并用传播概率与度数的乘积表示节点的直接影响力,其计算式为：

(3)

式中：deg(u)表示节点u的度数；puv是u通过边影响v的概率；neighbors(u)表示节点u的邻居节点集合。

式(3)中我们考虑了传播概率对节点影响力的影响。需要注意的是,在真实的社交网络中,节点之间的传播概率并不是固定值,而是在区间[0,1]内变化的。同时,文献[18]也证明了传播概率在等于区间的右边界或左边界时,传播模型将达到最差的性能。

考虑到具有高中心性的节点更容易影响到具有低中心性的节点,本文使用网络中每条边的两个节点的中心性去计算传播概率p[13]。节点u影响v的概率为：

(4)

Eu和Ev的值本文分别采用节点u和v的特征向量中心性来计算,其计算式为：

(5)

式中：λ表示邻接矩阵的最大特征值；xi是节点；ai,j是节点xi、xj之间的权重,特征向量中心性是根据节点的中心性计算它们的权重,然后将与当前节点可达的其他节点的权重的线性和视为该节点的中心性值[19]。

同时,节点邻居的拓扑连接对节点的影响力度量也是有影响的,对于中心性相同的节点,若其邻居密度较高,则有更多的相互影响的机会,因此邻居密度较高的节点会具有更强的扩展能力[7]。另外,考虑到全局度量的计算复杂度高,将其应用于大规模社交网络时间复杂度高,因此用节点的局部聚类系数度量邻居之间的拓扑连接,并将其表示为节点的间接影响力,其计算式为：

(6)

式中：cv表示节点v的聚类系数。局部聚类系数等于节点v的邻居节点之间连边的数量与邻居节点之间可达连边的最大数量之比[20]，其计算式为：

(7)

式中：Nv为节点v的邻居节点集合；deg(v)是节点v的度数。

基于以上阐述,节点之间的度数和传播概率以及节点邻居的拓扑连接对节点的扩展能力都有影响,则节点的局部传播中心性(LPC)计算式为：

C(u)=C1(u)+C2(u)=

(8)

式中：C1(u)表示度量节点的直接影响力；C2(u)表示度量节点的间接影响力；deg(u)表示节点u的度数；cv表示节点v的聚类系数；puv是u通过边影响v的概率。

局部传播中心性(LPC)的核心思想如下所述。首先用传播概率量化节点的实际传播过程, 用节点的度数与传播概率的乘积表示当前节点的直接影响力,其次用聚类系数度量当前节点邻居的拓扑连接,并表示对节点的间接影响力。最终,节点的影响力就是直接影响力与间接影响力的求和。

2.2 IMLPC

度和其他基于度中心性的启发式算法常用于解决影响力最大化问题,但是其影响范围有限。因此本文利用局部传播中心性(LPC)衡量每个节点的扩展能力,并提出IMLPC,该算法的种子节点选择依赖于每个节点的局部传播中心性(LPC)计算结果。在选择网络中的k个节点构成种子集S时,选择当前迭代中局部传播中心性(LPC)最大的节点作为种子节点。

算法1IMLPC

输入：社交网络G(V,E),传播概率P,节点聚类系数C,种子集大小k。

输出：种子节点集合S。

1．InitializeS=∅

2．For each nodeudo

3． Calculate its degreedu；

4．lpcu=du；

5．End For

6．Fori=1 tok

7． Selectu=argmaxu{lpcu|u∈VS}；

8．S=S∪{u}；

9. For each neighborvofuandu,v∈VS,puv∈P,cv∈C,do

11． End For

12．End For

13．Output S

在IMPLC中,算法的输入为图G(V,E),种子节点数k,由式(4)计算得到节点之间传播概率P,以及由式(7)计算得到的每个节点的聚类系数C,输出为最终选择的种子集S。算法第1行初始化种子集S为空。第2-第5行,计算所有节点的度数,并让每个节点的局部传播中心性(LPC)等于其度数。第6-第12行,由式(8)计算每次循环中节点的局部传播中心性并将计算结果最大的节点添加到种子集S中。第13行,输出种子集,算法结束。

算法1利用启发式策略,选择局部传播中心性最大的k个节点作为种子节点,因此可以保证算法运行时间,同时选择种子节点时考虑了传播概率,算法的精度也有所提高。

3 实 验

3.1 数据集介绍

由于本文讨论在线社交网络,因此实验中用到的所有数据集都是从在线社交网络收集的。为了解决影响传播模型中的噪声问题,选择两种不同规模的数据集进行实验。MIT数据集是从在线社交网站Facebook收集的数据集,包含在麻省理工学院学习的Facebook用户,该数据集中用户之间的联系比较紧密。douban数据集是由LongQiu (lqiu4@asu.edu)从豆瓣网站(Douban.com)爬取的友谊网络。详细信息如表1所示。

表1 数据集介绍

3.2 对比算法及实验环境

本实验运行环境为：CPU为3.40 GHz Inter Core i7,内存10 GB,操作系统为Windows 10,本文算法使用Python语言编程实现。

本文采用IC模型模拟种子集的影响范围,采用蒙特卡罗(Monte-Carlo)模拟了1 000次实验,然后得到影响范围的平均值。为验证IMLPC的性能,与其他算法进行实验对比,对比算法如表2所示。

表2 对比算法基本介绍

3.3 结果分析

本文主要从种子集的影响范围和算法的运行时间两方面衡量算法的性能，对IMLPC和四个对比算法在两种不同的数据集上进行评估。

3.3.1 影响范围对比

图1和图2分别描述了本文提出的IMLPC以及DegreeDiscount、Degree、EigenvectorCentrality和NewDiscount四个对比算法在MIT和douban数据集上的种子集影响范围。

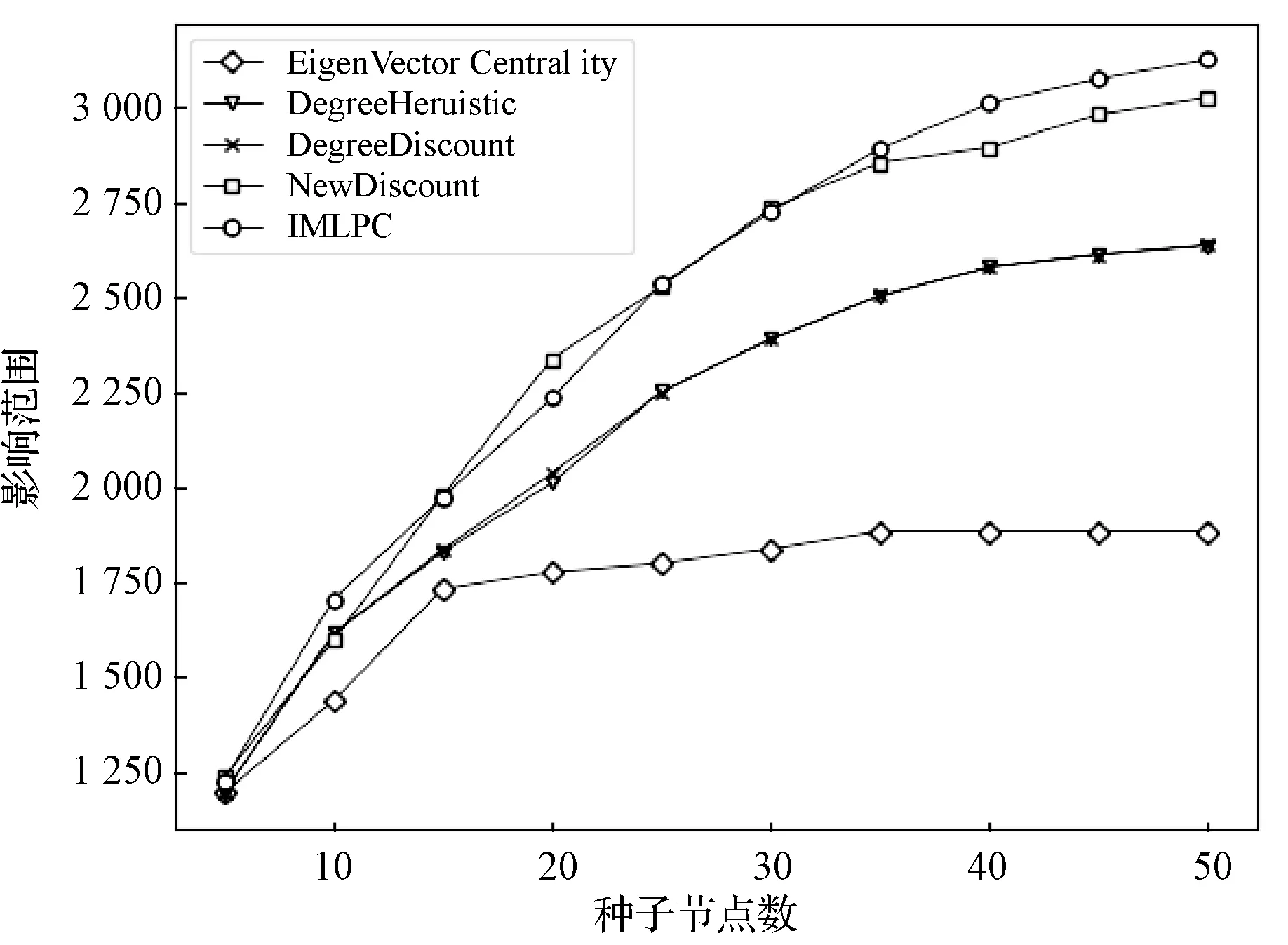
图1 不同算法在MIT数据集上的影响范围

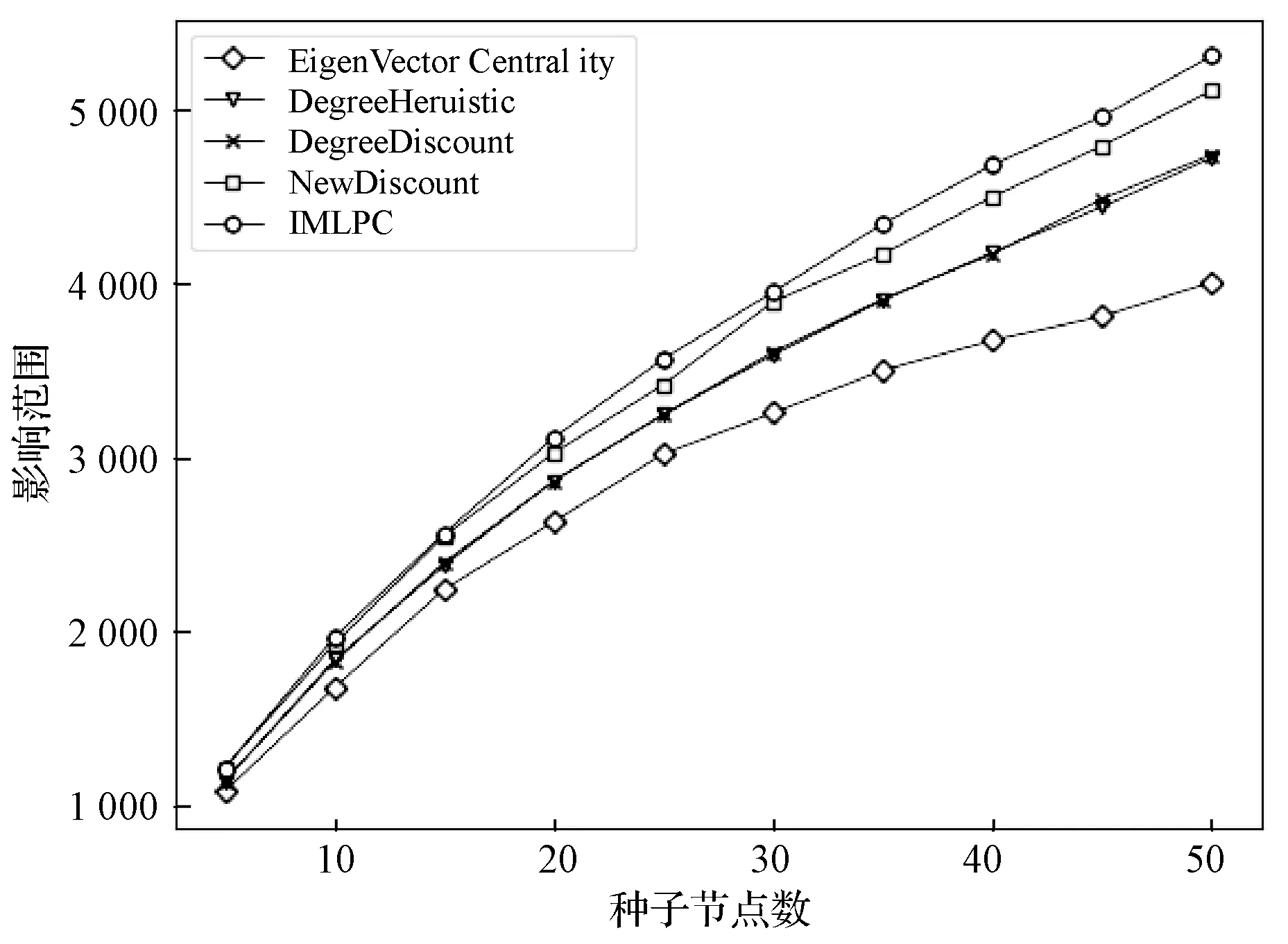
图2 不同算法在douban数据集上的影响范围

通过比较不同数据集上的影响范围,可以发现EigenvectorCentrality的影响范围较低。例如,当k=10时,其影响范围在MIT和douban数据集上分别低于IMLPC15.6%和14.8%。本文提出的IMLPC在两种数据集上的影响范围明显优于其他算法,这也表明传播概率和节点拓扑连接对节点影响力的度量有很重要的作用,例如在douban数据集上,当k=40时,IMLPC的影响范围较DegreeDiscount、Degree、EigenvectorCentrality和NewDicount算法分别提高10.9%、10.7%、21.6%和3.9%。在MIT数据集上;当k=40时,IMLPC的影响范围较DegreeDiscount、Degree、Eigenvector Centrality和NewDicount算法分别提高14.3%、14.3%、37.4%和3.9%。虽然在MIT数据集上,IMLPC在k=20时影响范围略微低于NewDicount算法,但在整体上仍然较好,因为在实验中当k>24时,IMLPC的影响范围会高于NewDiscount算法,并且在此之后,IMLPC都优于NewDiscount算法。综上所述,IMLPC的影响范围是优于其他启发式算法的,该算法适用于大规模社交网络。

3.3.2 运行时间对比

算法的运行时间同样是衡量算法性能的一个因素,算法的运行时间会因为不同数据集的特征而有所不同。图3和图4分别描述了种子节点数k=10、30和50时,IMLPC和其他4个对比算法在MIT和douban数据集上的运行时间。

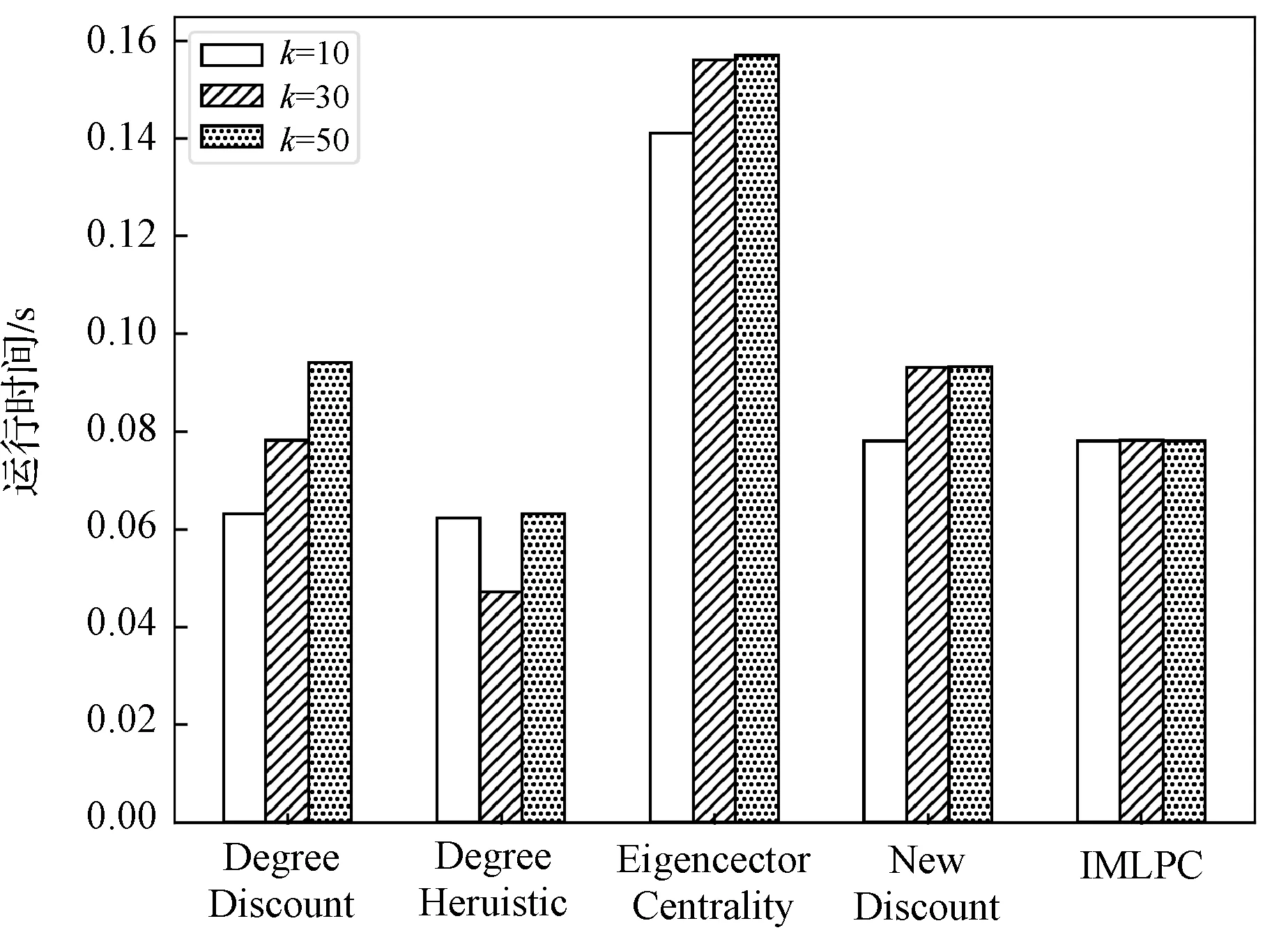
图3 不同算法在MIT数据集上的运行时间

图4 不同算法在douban数据集上的运行时间

可以看出,IMLPC算法与EigenvectorCentrality和NewDiscount算法相比,在不同数据集上的运行时间都有所提高。例如在规模最大的douban数据集上,k=30时,IMLPC的运行时间较Eigenvector Centrality、NewDiscount算法相比分别提高了8.8%、3.1%；k=50时,分别提高了11.3%和3.1%。IMLPC与DegreDiscount和Degree算法相比,在MIT数据集上的运行时间接近；在douban数据集上的运行时间相差在0.3 s,可能的原因是douban数据规模更大,IMLPC在度量节点的影响力时,需要多次对节点邻居的聚类系数进行累加运算,导致运行时间稍长。但是,IMLPC在douban数据集上的影响范围是明显优于DegreeDiscout和Degree算法的,所以相差的运行时间仍在可接受范围内。

随着种子节点数k增大,IMLPC相对于其他对比算法的影响范围会越来越大。在大规模的douban数据集上效果更加显著。IMLPC的运行时间与其他对比算法都十分接近,甚至会有所提升,并且IMLPC的运行时间会随着k的不断增加而趋于稳定。说明该算法适用于在大规模社交网络中去解决影响力最大化问题。

4 结 语

本文针对度中心性等方法选择种子节点时未考虑节点间传播概率及邻居拓扑连接的影响,提出LPC方法度量节点影响力,该方法用传播概率量化节点的实际传播过程,同时用节点邻居的拓扑连接度量节点的间接影响力。然后提出基于局部传播中心性的影响力最大化算法(IMLPC)。实验结果表明,IMLPC在IC模型上的影响范围相对比现有启发式算法有显著提升,且算法的运行时间也有所改进,验证了算法的有效性和可行性。未来考虑使用除节点的属性外的知识(如机器学习等)更加准确地量化节点间的传播概率,并减少传播模型的随机性。