流固耦合作用下含缓倾软弱夹层边坡稳定及参数敏感性研究
2023-03-15杨启帆马利遥王泽祺曹建军
杨启帆 胡 斌 马利遥 刘 霁 王泽祺 曹建军
(1.武汉科技大学资源与环境工程学院,湖北 武汉 430081;2.冶金矿产资源高效利用与造块湖北省重点实验室,湖北 武汉 430081)
在中国西南地区二叠系沉积石灰岩地层中,存在 着厚度通常为10~30 cm 的缓倾炭质泥岩软弱夹层、缓倾炭质页岩软弱夹层[1],此类软弱夹层呈区域性分布[2],其内部结构疏松,颗粒间连接力薄弱。西南地区降雨丰沛,软弱夹层经受雨水反复浸泡疏干,吸水膨胀、失水收缩长期循环,进而导致软弱夹层崩解破坏,力学性能极低,该类软弱夹层往往会成为边坡致滑的优势结构面[3-7]。软弱夹层中存在应力场与渗流场交互作用,流固耦合在两者相互作用下形成,在影响边坡稳定的因素中,流固耦合问题是众多学者研究的重点和难点[8]。由于不同区域缓倾软弱夹层形成的地质条件和组成成分不同,从而软弱夹层相关参数(倾角、厚度、内摩擦角、黏聚力等)存在差别,在渗流场和应力场耦合作用下软弱夹层力学性质相对于自然状态亦会产生变化,因此流固耦合作用下缓倾软弱夹层参数特征的研究成为边坡稳定性分析与治理工作中需要进一步研究的问题[9-10]。
许多学者对于单因素作用下含软弱夹层岩质边坡稳定性的影响做了长期大量研究,李亚鹏、边疆、陈权川等[11-13]通过对软弱夹层参数的敏感性分析,确定边坡稳定性受各参数的影响程度。对于边坡稳定性受流固耦合作用的影响方面,众多学者在相关领域进行了深入研究,探索出值得后人借鉴的研究方法,如肖秀丽[14]从多孔介质渗流理论出发,将所建立的流固耦合渗流有限元模型应用于土坝并进行坝坡稳定性分析;刘垭均[15]依托具体工程实例,基于强度折减法与流固耦合在有限元软件上的结合,得到不同工况下的边坡安全系数并分析了边坡材料参数对于边坡安全系数的影响;张晨等[16]运用流固耦合有限元方法,以实际工程为原型分析了该边坡的长期稳定性并提出优化方法。
以上研究表明,现阶段大多数文献主要集中在以下两方面,一为单因素作用下缓倾软弱夹层参数对边坡稳定性的敏感程度分析,二为基于流固耦合作用下的边坡稳定性研究,但是对于流固耦合作用下含缓倾软弱夹层边坡稳定性研究比较缺乏。鉴于此,本研究通过正交试验设计,利用有限差分软件FLAC3D对简化的含缓倾软弱夹层岩坡模型进行稳定性系数计算[13,17],对流固耦合作用下的计算结果分别运用极差分析和单因素敏感性分析,确定缓倾软弱夹层参数敏感性权重排序,为考虑流固耦合作用下含缓倾软弱夹层边坡稳定性防控与治理提供有效参考依据和指导。
1 基本原理
1.1 基于FLAC3D 的强度折减法
本文主要通过FLAC3D采用强度折减法计算流固耦合作用下含缓倾软弱夹层矿山边坡稳定性系数,根据四川省金顶黄山石灰石矿山现场采样进行力学试验所得到的物理力学指标,对坡体材料的黏聚力c和内摩擦角φ进行折减,使得坡体内部产生符合屈服准则的区域,即塑性区。当塑性区贯通时,表明坡体发生了不可逆转的塑性流动破坏,此时折减系数即为边坡稳定性系数F[13],其表达式为
在FLAC3D中采用二分法对抗剪强度参数c和φ进行折减,且参数折减的精度与FLAC3D默认的收敛标准(或称相对收敛标准)有关。在数值计算过程中,定义无量纲值R确定收敛标准,其表达式如式(3)所示。随着计算的进行,体系最大不平衡力逐渐趋向于零,取R<10-5作为收敛标准。
1.2 基于FLAC3D 的流固耦合理论
含缓倾软弱夹层岩质边坡中存在着渗流场,考虑渗流场和应力场耦合作用对岩坡的影响主要采用饱和—非饱和渗流理论进行研究。在宏观尺度的研究上,渗流过程遵循达西定律,建立如式(4)所示的孔隙压力与流体渗流速度的关系以及如式(5)所示的岩土体应力—应变之间的关系,以实现流固耦合计算。由达西定律v=k·i给定渗流速度qi计算公式[18]如下:
式中,kil为绝对渗透系数;(s)为相对渗透系数;p为孔隙水压;ρf为流体密度;gj为重力加速度。
运用FLAC3D计算时,仅设置应力场与渗流场存在,其本构方程[19]可表达为
式中,M为比奥模量;n为孔隙率;s为饱和度;α为比奥系数;ζ为流体容量;ε为体应变。
在渗流模式中,平衡方程求解不涉及大变形计算,单位时间内的微元体含水量变化值通过式(6)计算[18]得出。
式中,qv为微元体流体流入量;ζ为单元流体体积变化值。
2 工程应用实例
四川省金顶黄山石灰石矿山边坡主要为厚层二叠系下统梁山组、栖霞组和茅口组水泥用石灰岩,金顶黄山石灰石数字化矿山模型如图1 所示,坡体内含有数层倾角小于25°的炭质泥页岩缓倾软弱夹层。

图1 金顶黄山石灰石矿数字化模型Fig.1 Digital model of Jinding Huangshan Limestone Mine
由于整个坡体延伸范围较大,为避免贯穿裂隙以及坡形等因素对边坡稳定性计算结果产生影响,对计算模型进行合理简化。根据郑颖人等[20]提出的模型建立原则,结合本研究实际情况,建立如图2 所示的简化模型。在简化模型中,坡高H为20 m,CD=1.5H=30 m,AB=2.5H=50 m,坡底向下延伸高度DE=1.5H=30 m,模型总宽度为100 m,坡角为45°,令坡面与软弱夹层的交点至坡脚的垂直距离为10 m且保持不变,软弱夹层倾角为β。

图2 边坡简化计算模型Fig.2 Slope simplified calculation model
计算分析时采用Mohr-Coulomb 屈服准则,边坡岩体与缓倾软弱夹层视为含均匀孔隙的各向同性介质。计算模型单元网格划分如图3 所示,该模型共划分单元数6 725 个,节点数8 448 个。模型划分单元数和节点数由于缓倾软弱夹层厚度以及倾角的改变而有稍许变化。模型边界约束如图4 所示,下部边界为全约束,左右边界为水平约束。

图3 模型单元网格划分Fig.3 Model element meshing

图4 模型边界约束Fig.4 Model boundary constraints
运用FLAC3D进行流固耦合分析计算时,采取渗流进程和力学进程都打开的模式进行求解,以缩短计算时间,加快计算进程。求解流程如图5 所示,在定义计算模型并赋予岩土体参数后,打开渗流模块(CONFIG fluid),使计算模型加入渗流场。对计算模型施加边界条件,边坡临空面设置为透水边界,其余部分为不透水边界,以此达到确定孔隙水压力边界的目的。在施加初始应力以及施加初始孔隙水压力后使用直接求解法在渗流模式(SET fluid on)和力学模式(SET mech on)都打开的状态下直接利用solve 命令进行求解,其中set mech 命令控制力学进程,set fluid 命令控制流体进程。

图5 FLAC3D 流固耦合求解流程Fig.5 FLAC3D fluid-structure interaction solution flow
本研究结合强度折减法和二分法进行边坡简化模型稳定性系数的计算,由于渗透系数在有限差分软件和土力学中的含义不同,计算时利用式(7)进行渗透系数单位的换算[19]。
流体渗流参数取值[18]如表1 所示,计算时采用各向同性渗流模型。

表1 流体渗流参数取值Table 1 Fluid seepage parameter values
3 正交试验设计及敏感性分析
正交试验设计是利用正交表来安排与分析多因素试验,寻求最优水平组合的一种高效率试验设计方法。通过对多因素多水平试验科学地筛选组合参数,于试验因素所有水平组合中选取部分代表性水平组合开展试验,对该部分试验结果进行分析,从而认识到总体试验情况,并确定最优水平组合。
本研究依托四川省金顶黄山石灰石矿山边坡稳定性治理项目,基于正交试验基本原则,选取缓倾软弱夹层倾角、厚度、内摩擦角、黏聚力作为试验因素,并且不考虑4 个典型参数之间的交互作用,根据实际工况确定各因素均为4 个水平。软弱夹层及石灰岩体的物理力学参数[21]如表2 所示,各影响因素及其水平下取值如表3 所示。

表2 岩土体物理力学参数Table 2 Physical and mechanical parameters of geotech body

表3 影响因素及水平Table 3 Factors and levels
本文选用正交试验表L16(45)来安排与分析4 因素试验,即在不影响试验结果的前提下需要安排至少16 次试验。正交试验参数组合及其试验结果如表4所示。
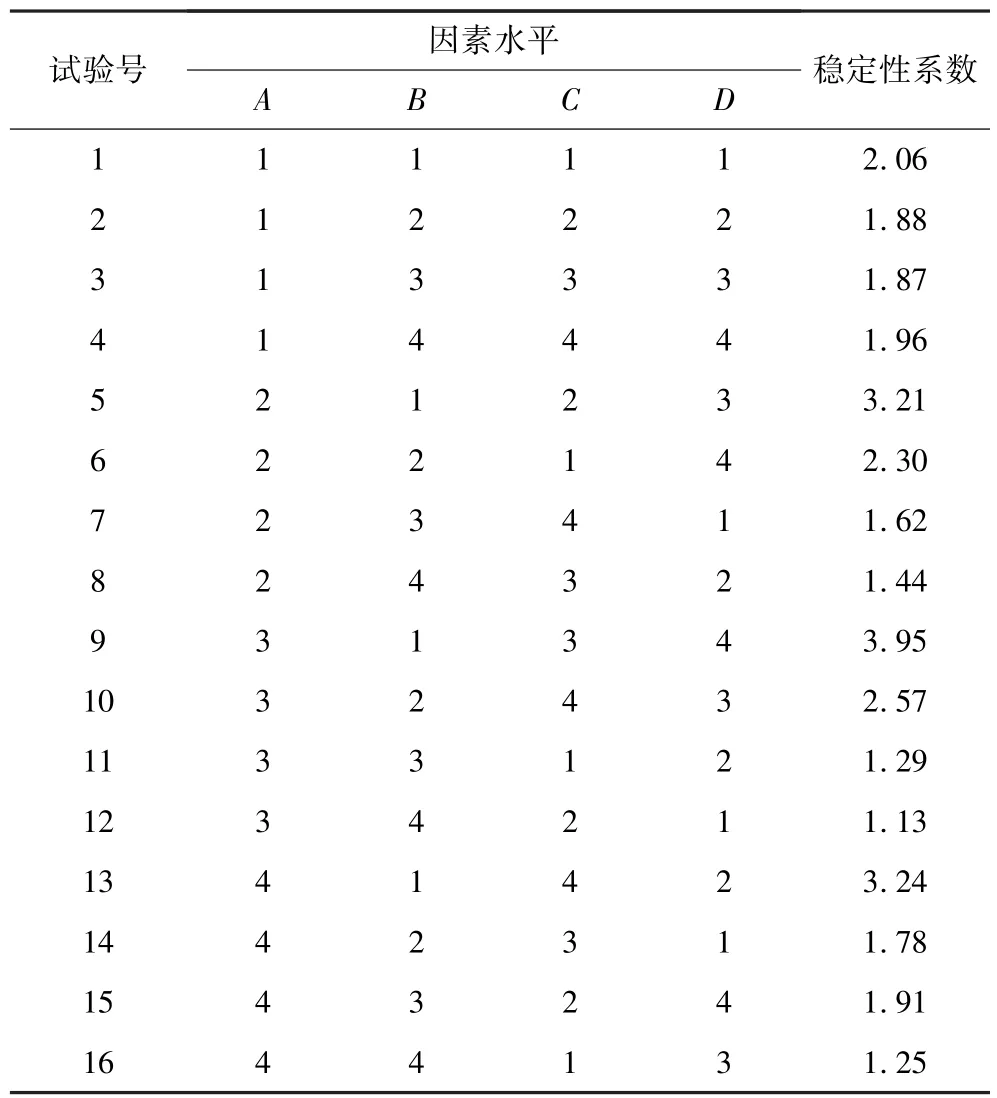
表4 正交试验方案及结果Table 4 Orthogonal test scheme and results
3.1 极差分析
极差分析方法流程如图6 所示,该方法是正交试验结果分析最常用的分析方法,具有计算简便、直观形象的特点,通过计算因素极差值来判断其影响程度大小以及某因素的最佳水平情况。
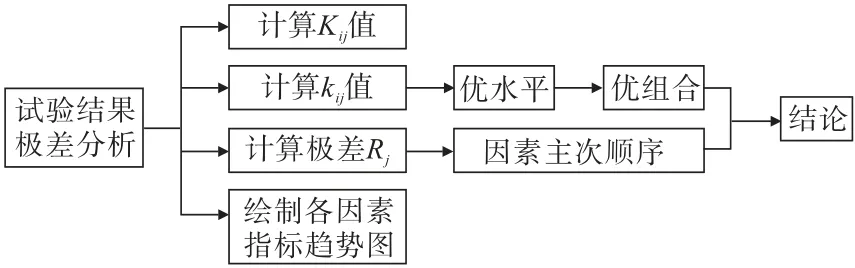
图6 极差分析流程Fig.6 Flow of range analysis
进行极差分析时,Rj表示各因素极差,K1j、K2j、K3j、K4j分别表示A、B、C、D因素下第1、2、3、4 水平所对应的试验指标之和,k1j、k2j、k3j、k4j分别表示K1j、K2j、K3j、K4j所对应的平均值,极差Rj可由式(8)计算得出,利用最大均值与最小均值之差反映出各因素水平波动时试验指标的敏感性。
正交试验极差分析结果如表5 所示。由表5 得到,考虑流固耦合作用下含缓倾软弱夹层的石灰石矿山边坡中4 个典型参数敏感性权重排序依次为B>D>C>A,即4 个典型参数对边坡稳定性的影响程度排序为:倾角>内摩擦角>黏聚力>厚度。根据各因素水平极差值可知,当软弱夹层倾角为10°,内摩擦角为27°,黏聚力为25 kPa,厚度为0.22 m 时,边坡稳定性最好,即该正交试验中最优水平组合为B1D4C4A3。

表5 各因素极差分析结果Table 5 The results of the range analysis of various factors
各因素各水平稳定性系数均值如图7 所示。根据各影响因素各水平稳定性系数均值图可以推断出,尽管流固耦合作用下软弱夹层厚度对边坡稳定性影响程度最小,但是由图7(a)可以看出,并非软弱夹层厚度越大,边坡越稳定。当厚度超过某个临界范围时,边坡稳定性降低,这是因为软弱夹层经受雨水长期浸泡,随着软弱夹层厚度增加,其含水量增大,软弱夹层出现泥化状态,具有较高的塑性,其力学性能降低,从而使边坡稳定性变差。由图7(b)知,随着软弱夹层倾角逐渐变小,边坡稳定性趋向于更高状态。由图7(c)知,随着软弱夹层黏聚力的增加,边坡稳定性可能减小也可能增加,根据文献[10,13,17]研究结果可知,边坡稳定性随着软弱夹层黏聚力的增加而增大。而结合本文实际工况,软弱夹层受到雨水反复浸泡疏干,吸水膨胀、失水收缩不断循环,在此过程中软弱夹层内部颗粒间连接力不断变化,因而边坡稳定性也在变化。但是,从整体趋势来看,软弱夹层黏聚力越大,边坡越趋向于稳定。由图7(d)知,随着软弱夹层内摩擦角逐渐变大,边坡趋向于稳定性更高状态。

图7 各因素各水平稳定性系数均值Fig.7 Stability factor average values of each level of each factor
3.2 单因素敏感性分析
单因素敏感性分析是通过变动单个因素来观察整个试验结果的变化情况。由于缓倾软弱夹层4 个特征参数的量纲不同,无法直接进行比较。将表5 中各个参数的极差相对变化率作为稳定性系数的相对变化率,参照表3 取各影响边坡稳定性因素水平下的相对变化率[10]进行敏感度计算。
假设边坡稳定性系数为gi=g(x1,x2,…,xn),令,边坡稳定性影响因素敏感度Si利用式(9)计算。由式(9)可知,某一因素对边坡稳定性的影响程度随着敏感度Si的增加而提高。
流固耦合作用下各因素敏感度计算结果如表6所示,在各个因素相互独立的情况下,软弱夹层代表性参数敏感性排序结果与极差分析结果一致,进一步验证了在流固耦合作用下缓倾软弱夹层倾角的敏感性权重最高,内摩擦角和黏聚力的敏感性权重比倾角的敏感性权重低,厚度的敏感性权重最小。

表6 敏感度分析结果Table 6 Sensitivity analysis results
4 结论
针对我国西南地区含缓倾软弱夹层岩质边坡典型相关参数在流固耦合作用下对边坡稳定性的影响程度,以四川省金顶黄山石灰石矿山边坡为研究对象,基于数值模拟方法,以流固耦合理论为指导,结合正交试验、极差分析和单因素敏感性分析方法,得到以下研究结论:
(1)根据正交试验极差分析结果得到在流固耦合作用下含缓倾软弱夹层岩质边坡中4 个典型参数对边坡稳定性的影响程度排序为:倾角>内摩擦角>黏聚力>厚度。根据各影响因素水平稳定性系数均值图可知,并非厚度越大边坡越稳定,当厚度超过某个范围时,软弱夹层内部含水量增大,表现出泥化状态,塑性较高,力学性能降低,从而边坡稳定性降低;随着软弱夹层倾角逐渐变小,边坡趋向于稳定性更高状态;软弱夹层黏聚力增加,边坡稳定性可能减小也可能增大,这是因为软弱夹层吸水膨胀、失水收缩不断循环导致其内部颗粒间连接力不断变化,因而边坡稳定性变化;随着软弱夹层内摩擦角逐渐变大,边坡趋向于稳定性更高状态。
(2)根据单因素敏感性分析结果得到在流固耦合作用下4 个影响因素对缓倾软弱夹层敏感性排序为:倾角>内摩擦角>黏聚力>厚度,即流固耦合作用下缓倾软弱夹层倾角的敏感性权重最高,内摩擦角和黏聚力的敏感性权重比倾角的敏感性权重低,厚度的敏感性权重最小。
(3)流固耦合作用下缓倾软弱夹层代表性参数敏感性排序结果与极差分析结果一致,结合2 种分析方法得出的结论可靠性更高,治理含缓倾软弱夹层边坡时应多加考虑软弱夹层倾角对边坡稳定性的影响,为其提供有效参考依据和指导。
