基于数字孪生的自动化立体仓库货位分配优化方法*

赵 巍，连泰湖，张 雷，张以成，冉 孟，刘欣怡

（1.天津职业技术师范大学，天津 300222；2.天津商业大学，天津 300134）

随着航空航天相关空间建设计划的不断推进，中国于2019年已成为卫星发射第二大国[1]。应未来高质量、大批量卫星发射的计划要求，卫星装备的生产模式正在朝着智能制造的方向发展。智能生产线在航空航天制造企业中的应用逐渐扩大，自动化立体仓库作为智能生产线的重要组成部分，通过其本身的灵活性和布局占领位置的特殊性，为整条产线的自动化需求提供了窗口，具有总控的作用。自动化立体仓库在智能生产线上的应用对航空航天产品实现智能制造、提质增效具有重要意义。

目前，国内外对自动化立体仓库各个方面的研究越来越多，其中货位分配 （Storage location assignment，SLA）系统化设计研究相对较少。陈月婷等[2]提出基于改进粒子群算法来解决货架的稳定性和出入库效率问题。马永杰等[3]用遗传算法求出动态货位分配和拣选路径优化的Pareto最优解，优化了模型中具有约束条件堆垛机容量和行驶速度以及在多任务作业周期中的出库问题。俞雷霖等[4]提出了一种求解自动化立体仓库货位分配与优化的混合禁忌搜索算法（Hybrid tabu search，HTS）对货位分配进行优化，从而提高立体仓库的运作效率。潘森等[5]提出比常见货位分配数学模型更接近实际应用的新的数学模型，采用遗传算法优化自动化立体仓库的入库货位分配方案。曾强等[6]引入货物系概念并按照货物系分配货位的方式确定同种货物的分散程度，基于分段交叉和单点变异实现遗传进化算法，设计了一种非支配排序遗传算法分段整数编码方法，解决了有货位载重约束的自动化立体仓库货位的分配问题。王厅长等[7]利用遗传算法，采用两级库位编码的方式对双深式立库的货位分配进行研究。杨玮等[8]对双载具和三载具两种设备配置下的货位分配问题进行分析，并采用改进遗传算法进行了仿真求解。Bertolini等[9]提出了一种基于模拟退火过程的元启发式算法，旨在优化金属自动化仓库检索阶段的性能。蔡安江等[10]以产品出入库效率、货架重心和产品聚集度为目标建立了货位分配数学模型，提出了一种改进混合蛙跳算法解决双向式自动化立体仓库货位分配问题。

现有的自动化立体仓库货位分配研究，大都是结合具体要实现的目标运用各类算法进行货位分配优化并进行仿真预测。近年来随着制造业数字化转型，智能生产线运用更加广泛，自动化立体仓库货位分配随着产线工艺排产要求而发生相应改变。本文提出一种基于数字孪生的自动化立体仓库货位分配优化方法，以数字化的方式建立了与物理实体高保真映射的数字孪生模型，通过实时交互、货物数据统计、仿真及智能优化，映射和优化自动化立体仓库货位分配，系统地考虑环境影响和综合效率，实现货物货位分配过程中分配存储率高、资源利用率高、综合效益最大化，能提高航空航天设备生产模式的智能化程度，提高产品生产效率。

1 智能生产线数字孪生系统架构

航空航天制造智能生产线以自动化立体仓库为核心，为了适应智能生产线的高效率要求，构建结合自动化立体仓库的智能生产线数字孪生系统，其主要由数据采集层、模型层、货位分配优化层、网络层、物理层和孪生层组成，如图1所示。

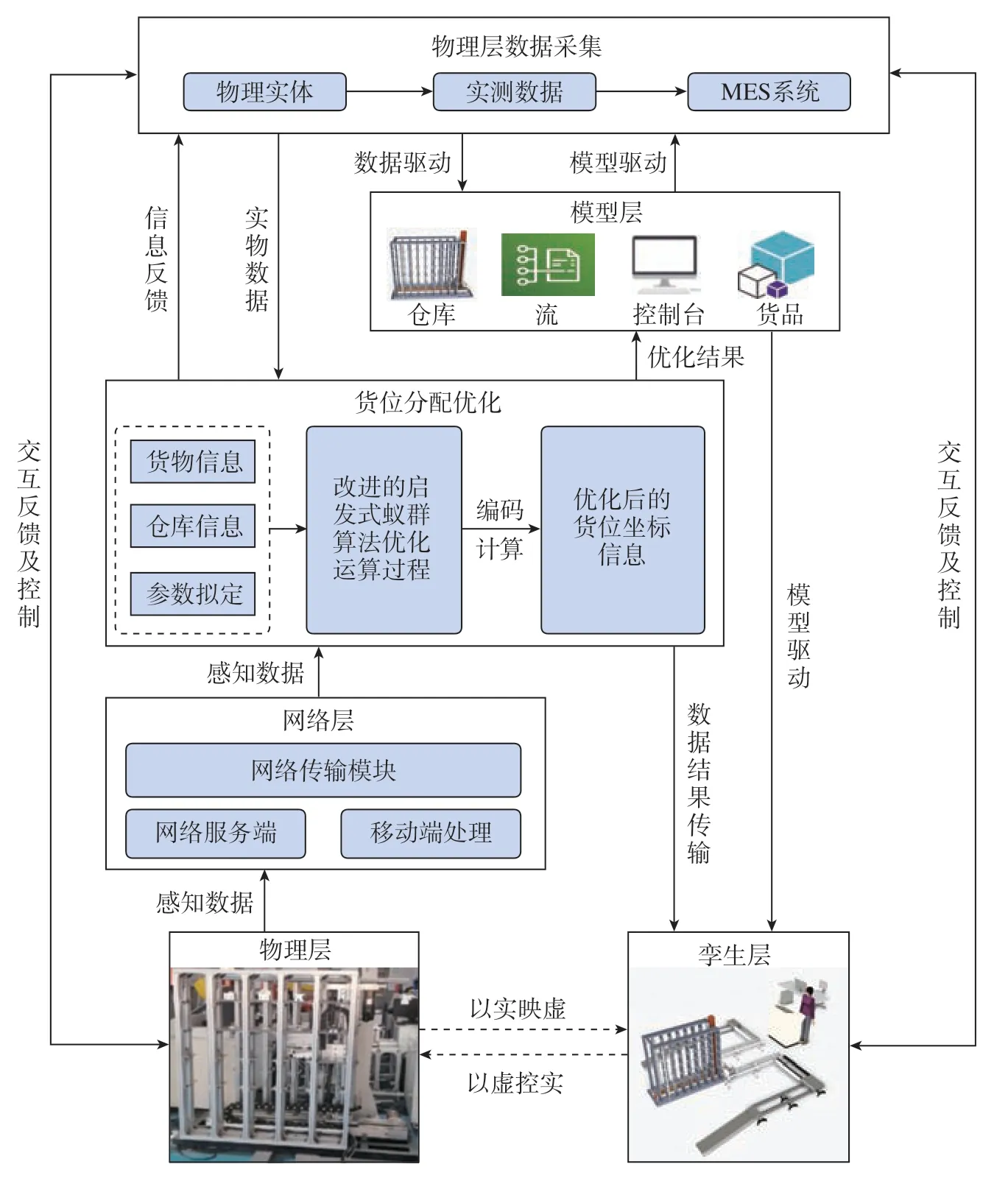
图1 数字孪生控制体系架构图Fig.1 Digital twin control architecture diagram

智能制造系统可适应规划仿真软件 （Visual engineering and education，VE2）兼具以下多种功能： （1）可以实现对上下位机传输信息的虚拟化处理与仿真，经由上位机程序与软件及数控系统的接口的设计与安装，保障物理实体与虚拟模型之间良好的通信与交互； （2）虚拟模型都按照实物真实比例和尺寸建立，具有的3D半物理建模、半物理示教程序和可适应规划模块保证其数字孪生功能的可实施性，保证半物理模型与实体的统一； （3）模拟驱动器具有数据采集和传输功能，具有信号连通性模块，在IO输入输出端口的辅助下，利用RFID技术将加工工艺货品信息传输到管理系统，再传输到仿真模型下的对应存储位置，然后实时将获得的立体仓库模型的输出信息及时传输给立体仓库的控制系统。

自动化立体仓库的结构比较复杂，其中包括堆垛机传输带、输送链条、升降滚轮、X轴移动机构、C轴旋转机构、Y轴货叉伸缩机构、Z轴升降机构以及货架，数控系统主要控制堆垛机运动。结合具体的目标控制需求，从已有的系统中调用宏功能可以更便捷、更快速地进行高效率控制，读取相关数字量信息采用TCP/IP协议，这种以太网驱动程序传输数据的方法实现较为简单，完全可以满足系统控制通信要求从而达到预期效果。控制过程流程如下。

（1）建立数据层与物理层之间的连接。物理实体具有适配数控系统且有协议适配接口，通过上位机与计算机端连接。

（2）状态信息采集。在物理系统中分布各类传感器，用以实现物理实体的数据分析，经由一系列的运作分析，将物理端数据采集并传输到数字孪生模拟端，在传感器功能数据采集、TCP/IP协议通信辅助下，数字孪生原型也能实现多维物理实体信息集成，通过模型的保真化模拟运行，实现对物理实体控制的准确性和高效性。

（3）堆垛机行驶速度调试。堆垛机半物理仿真模型与物理实体大小尺寸及其结构完全一样，设定虚拟模型初始化状态，使其跟物理实体初始状态完全一致，通过货位分配优化后输出的优化结果传输到模型层，为确保入库位置精准度，在半物理仿真场景下进行货位坐标编译，通过后台程序对其接收到的货位信息进行处理，再通过计算得到X轴移动机构、C轴旋转机构、Y轴货叉伸缩机构的具体移动距离的数值，确保模型控制的精准性，然后通过以太网连接，TCP/IP协议通信辅助下，通过上位机程序将模型层的数据传输到物理层的数控系统中，在数据传输保证实时性的理想状态下便可以保证虚拟仿真模型跟物理实体的实时同步。

2 货位分配优化模型

2.1 模型基本假设

智能生产线布局模式下的立体仓库两排货架之间设有一条巷道，巷道上有一台堆垛起重机穿梭在货架之间的巷道中，完成转载运送毛坯物料以及成品的工作，管理上采用计算机及RFID技术。自动化立体仓库布局结构俯视如图2所示。

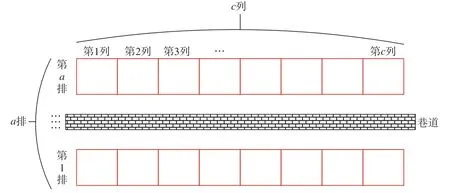
图2 自动化立体仓库布局结构俯视图Fig.2 Top view of automatic stereo warehouse layout structure

针对制造设备工艺流程智能加工产线自动化立体仓库货位分配遇到的相关问题和应遵循的原则，以工艺配置和管理系统下的产品工艺路线为基础，为了便于模型的建立和问题的研究，做出如下假设。

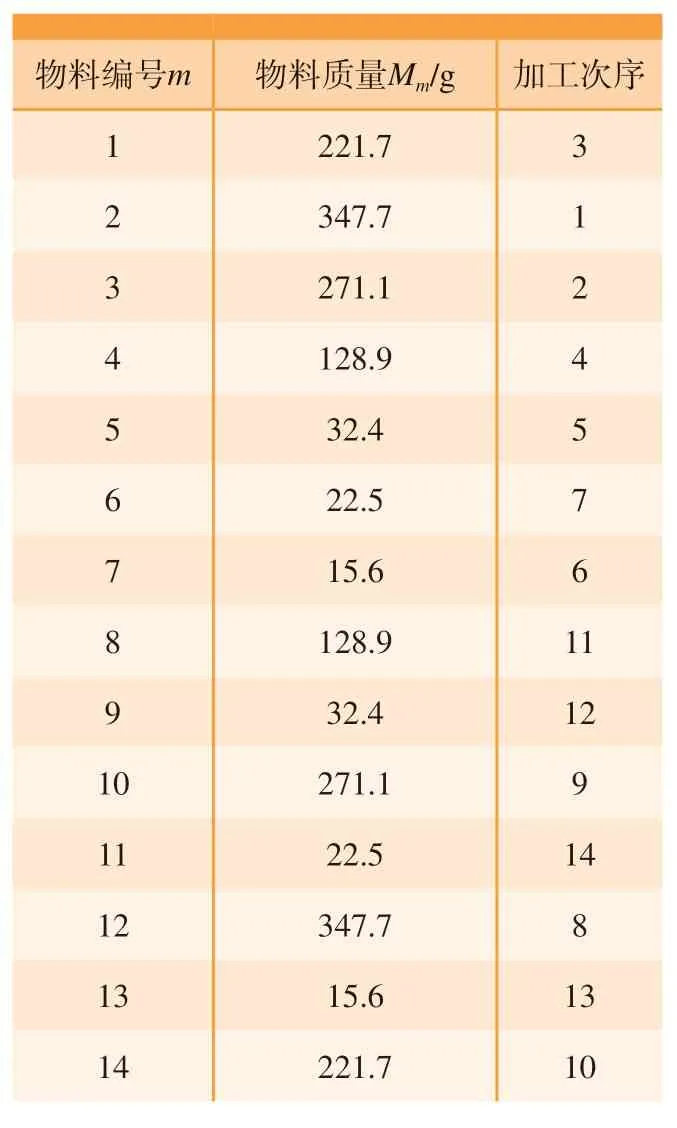
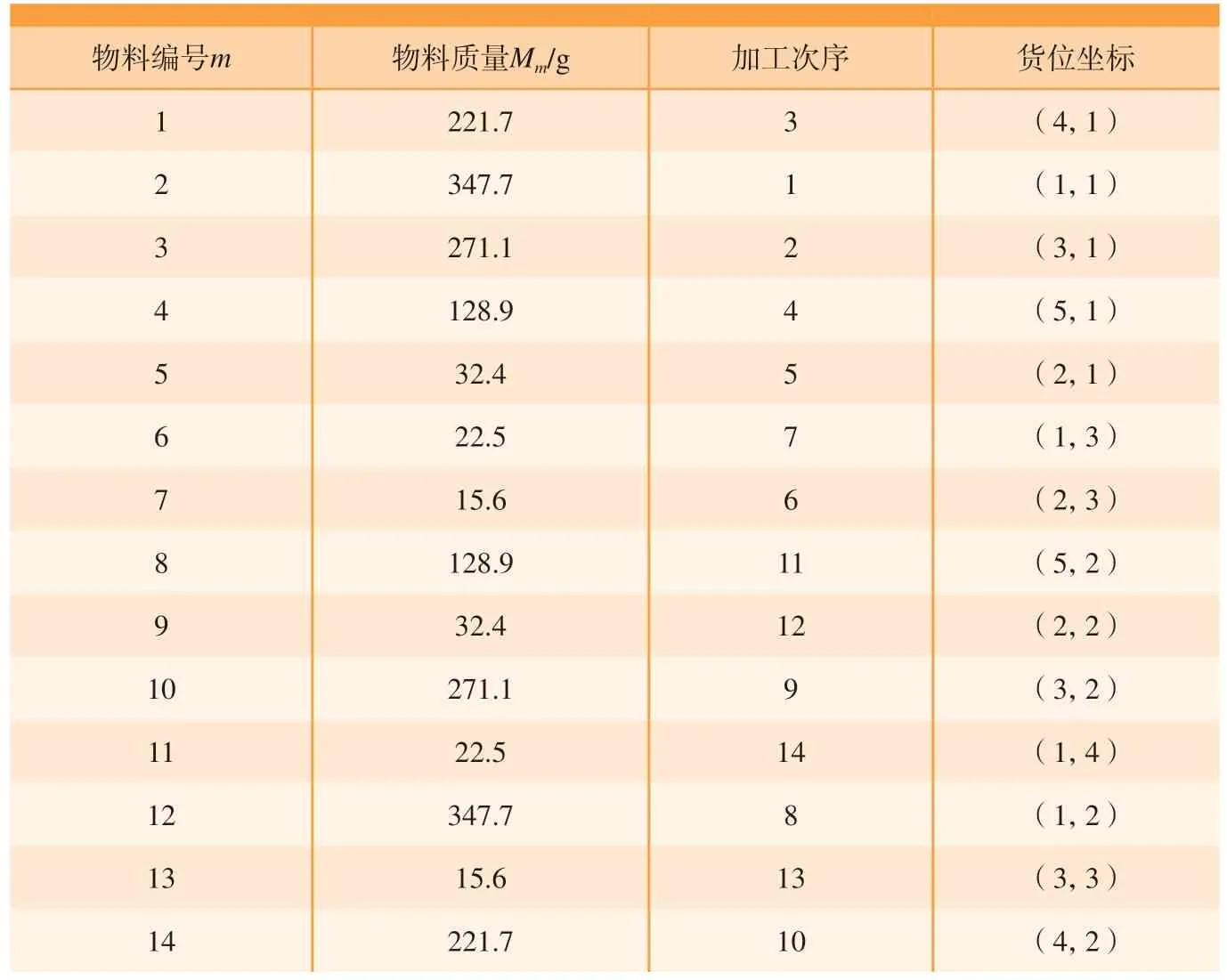
（1）定义（x，y，z，Tm，Mm）为某一待入库货物的信息，为了便于研究，仅考虑一组货架，假设两排货架有a排、b层、c列，且a= 2，b≤100，c≤100，定义左排货架左下角货位的左下角点为坐标原点，则货架的第x列、y排、z层的货位坐标表示为 （x，y，z），其中x≤100，1≤y≤2，z≤100，且均为整数。Tm为某种物料对应的加工次序；Mm为对应物料的质量；m为货品编号。

（2）假设每个货位的大小都相同且只能储存一件货品，并且货位长宽高都相等，设为L。

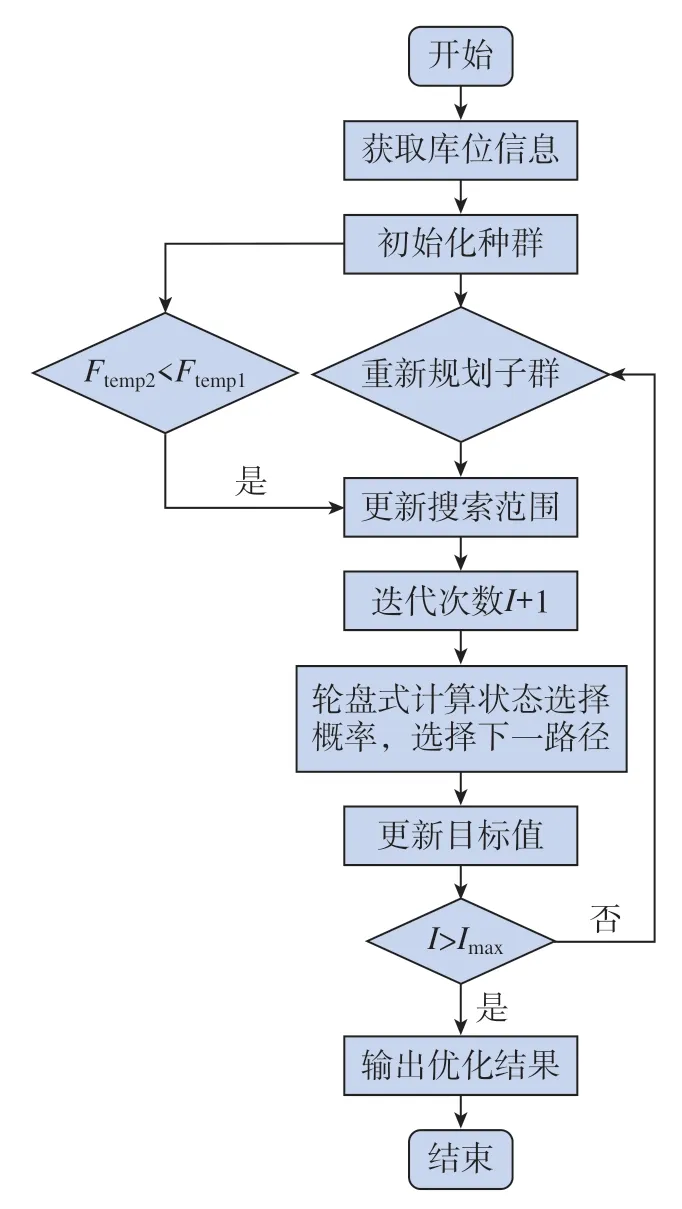
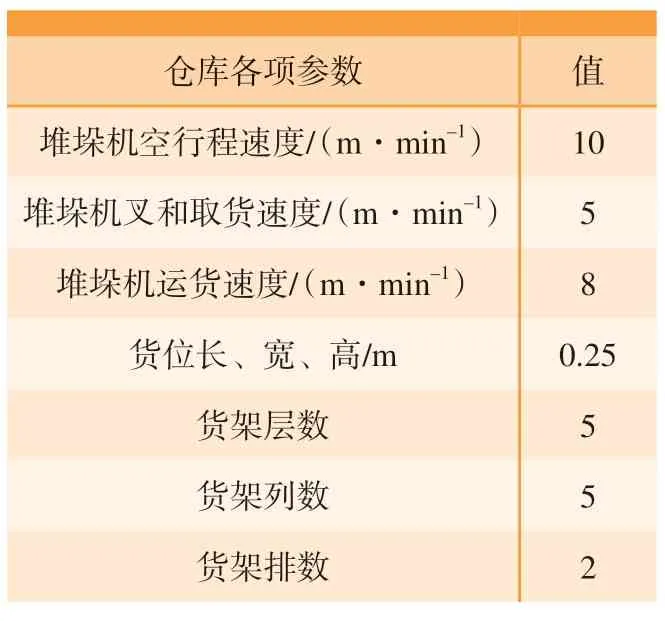
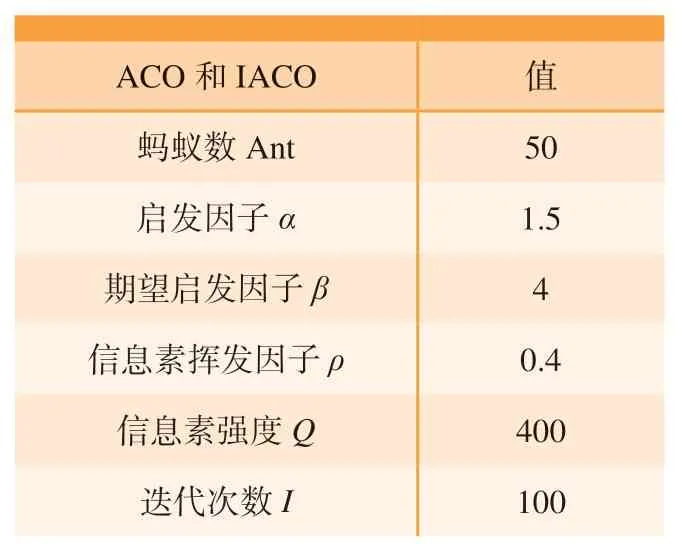
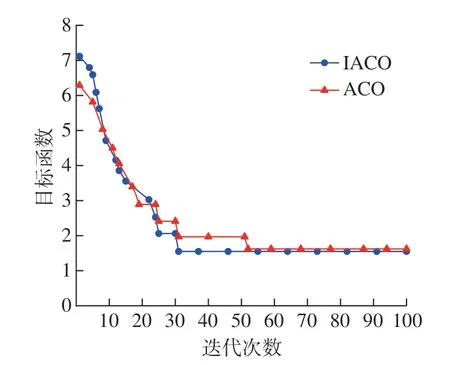
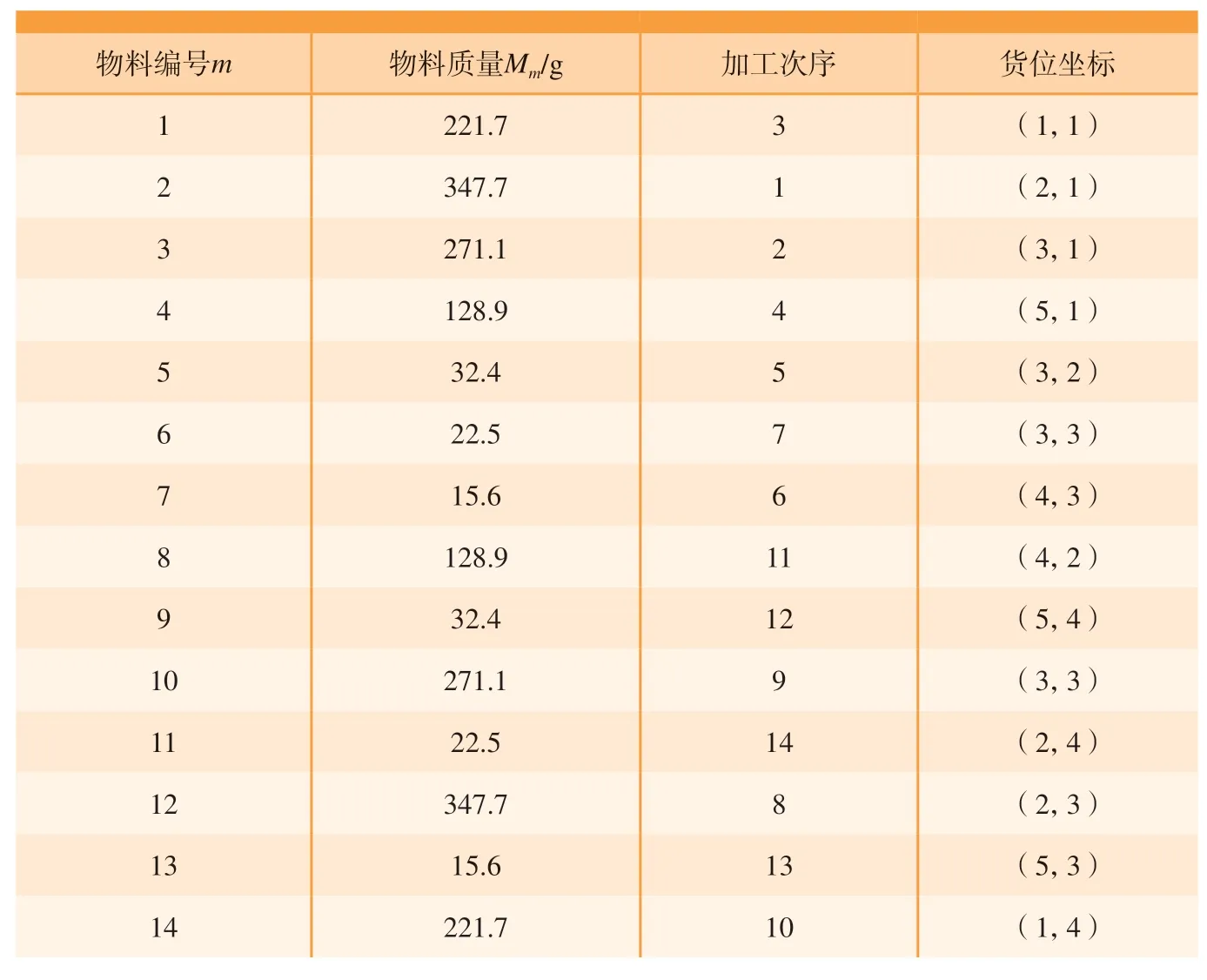
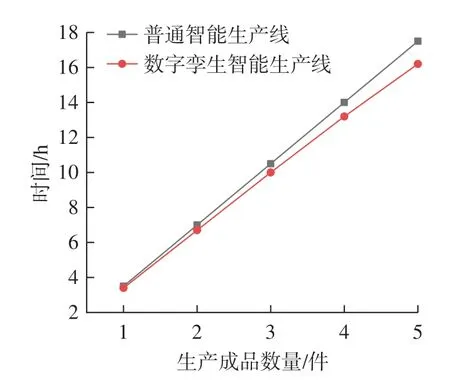
（3）假设堆垛起重机速度恒定，设其空行程、叉/放货、运货速度分别为Vk、Vc、Vy，且Vc

2.2 加工作业优化目标的定义

按工件加工工艺流程将堆垛机的调度问题归纳为：堆垛机由起点出发，拖取存在于m个不同货格的物料，堆垛机运动到一个货格，取出货位托盘及其托盘上的物料，再将托盘及其物料送到待加工物料存储的货格，然后再返回出发点，等到物料加工到规定工艺节点，堆垛机再去往下一个待加工物料货位点，且每个货格在存取过程中仅去一次，依次拣取完n个货物，再依次把加工完成的工件送回到储存位置，最后回到站台起点。

（1）以工艺排产次序为优化目标建立目标函数Q。

根据货区分配原则，智能制造过程中，排产计算和调度问题是影响货区分配的一个重要指标，最先加工的物料应该放在离出口最近的地方，待加工的毛坯物料应该按照具体情况尽量分配到出入库时间小的货位，有利于提升生产效率，减轻堆垛机工作压力。设某货位区编号为i，其中某种物料的加工次序数为Fi，时间评估系数按照计算公式Ii=s/Fi（s为货位中毛坯总数量）得出，其中s在具体工艺流程下为常数，且s≥1，时间评估系数越大，则应离出入口越近。要满足该原则，则分配优化目标就是使堆垛机运行时间最小，该策略的优化目标函数可描述为

（2）以相关货品聚集度为优化目标建立目标函数D。

根据货品相关性原则，同一种或同一种类型货品应按照具体情况尽量分配到相邻或相近的货位，能够减少堆垛机的行驶距离，其相关货品信息由载具定义标签决定，在货位分配过程中，RFID读写器发出标签芯片中的编码数据信息，然后通过无线网络将编码数据信息接入PC应用程序中进行数据解析、封装和传输，信息管理系统通过集成信息对货位进行初步规划。

若信息读取后货位要求存储某类产品时，定义此类货品分配存储区中心坐标为 （xi，yi，zi），要使该类待入库货品距离此货位最近，同类物料或者成品入库时必须为相邻货架，故两者之间的距离要尽量小。故该策略的优化目标函数可描述为

（3）以货架稳定性为优化目标建立目标函数S。

根据上轻下重原则，尽量将较重的货品放在货架的下面，降低货架重心以确保仓库货架的稳定性，即堆垛机在垂直方向上克服货物重力所做的功最小，其优化目标函数为

式中，g为重力加速度。

显然，3个目标函数各个参数互相影响，是典型的非多项式 （NP）难题，为方便后期处理，将其转换为单目标函数，并根据实际自动化立体仓库确定相关系数。总的优化目标函数为

2.3 启发式蚁群优化算法

除了数字化模拟引擎，数字孪生系统还包括一个联合优化模型。面向双目标的数字优化算法具有两个特点： （1）在短时间内快速识别最优或近似最优解，以适应生产系统和随机交付需求的高频率动态调整要求；（2）耦合优化问题的多个目标的协调，考虑到货位分配能力的稳定性，提出改进的启发式蚁群算法来提高货位分配运营效率。

20世纪90年代初期，受蚁群集体寻径行为的启发，意大利学者Dorigo等[11]提出了一种基于种群进化的启发式随机搜索算法——蚁群系统（Ant system，AS），并用于解决旅行商问题 （Traveling salesman problem，TSP），AS的初步试验取得了较好的结果，但无法与当时最好的TSP 求解算法竞争。经过演变后的蚁群算法（Ant colony optimization，ACO）获得了更好的计算性能[12–13]，可以解决更多的组合优化问题[14]。从人工智能 （Artificial intelligence，AI）角度来说，ACO是群智能算法的一个成功开端[15]。

蚁群算法是一种模拟蚁群智能行为的仿生优化算法，没有视觉的蚁群运动时会在通过的道路上释放出一种特殊的信息素[16]。堆垛机进行货位选择类似于蚁群觅食过程，碰到要选择的岔口时，就会根据信息素随机挑选一条路径，每只蚁群在所走过的路径上均会释放出等量的信息素，蚁群每次经过该路径均会释放信息素使得该路径上的信息素浓度增加；同时每条路径上的信息素随时间推移会逐渐挥发。因此，在初始点跟目标点之间，用目标函数代替初始信息素，按照约束条件进行迭代选择后，符合分配策略的路径信息素浓度较高，则下次迭代选择的概率更高，每次完整迭代一次后再采用新的信息素遗留信息，经过数次迭代后，则会根据约束条件得出最优分配货位。结合货位分配蚁群算法是指用来描述这一过程所组成的群体所表现出的极其复杂的行为特征的方法。传统蚁群算法的基本规则为

蚁群算法具有很强的正反馈能力，在算法后期能够加快算法的进化速度，促使算法迅速收敛，但在算法初期信息素匮乏，进化速度较慢。算法初期迭代循环一次更新下一代信息素过程若能增强信息素增量，则能避免前期信息素匮乏而导致进化速度慢的问题，因此，设计出以正弦函数为基础的信息素定量因子来解决这个问题。信息素更新公式修改为

式中，ωi（t+1）为下一时刻信息素总量；Q为常数，表示蚁群迭代循环一次释放的信息素总量；φ（t）是信息素定量因子。

式中，t为当前蚁群迭代次数，内函数1– e（1–t）在[1，+∞）上的值域为[0，1），则φ（t）在定义域内单调递减且值域为[1，2]，利用余弦复合函数的特点，在蚁群算法初期，φ（t）的值趋近于2，则初始信息素在算法初期就增长了一倍，即在算法初期增加了信息素总量，弥补了蚁群算法前期信息素匮乏而导致进化速度慢的问题；由于信息素定量因子φ（t）是关于迭代次数的函数，随着迭代次数的增加，函数值逐渐减小，最后趋近于1，即在算法中后期信息素迭代一次释放的信息总量趋于正常量，这就可以在算法后期确保算法的优势不随信息素定量因子而发生变化。这种信息素更新方式可以使算法初期迭代信息素增量更大，随着迭代次数的增加，信息素增量趋于稳定值，这就弥补了算法初期信息素匮乏的缺点，加快前期搜索速度，后期又保持了算法的准确性。

2.4 IACO算法求解步骤

针对建立的自动化立体仓库模型，采用启发式蚁群算法 （IACO算法）进行优化，流程如图3所示，算法的求解步骤如下。

图3 启发式蚁群算法流程图Fig.3 Flow chart of improved ant colony optimization algorithm

（1）获取自动化立体仓库当前的货位信息（空货位、已存货位和货品信息等）。

（2）初始化种群参数设置，即初始化蚁群位置，在可行范围内生成蚁群群总数为Ant、最大迭代次数Imax、当前迭代次数I、初始信息素T0、全局转移选择因子P0和信息素挥发系数P等。

（3）重新规划子群。若生成第一代子群，则根据状态转移概率让蚁群确定搜索方式，即全局转移概率Prob小于P0时进行局部搜索，Prob大于P0时进行全局搜索，再判断新位置函数值Ftemp2是否小于Ftemp1，是则更新搜索范围。

（4）信息素更新。在信息素更新中引入信息素定量因子，对蚁群留下的信息素进行更新。然后进行下一步迭代，迭代次数I=I+ 1。

（5）更新目标值。根据已经迭代后的结果信息判断状态信息，用最新一次迭代后生成的结果信息替换对应存储中的信息。将全局最优解存入目标矩阵中。

（6）判定终止条件。判断I>Imax，是则算法结束，输出全局最优解，否则返回步骤（3）重新规划子群，继续迭代。

（7）输出优化结果。画出蚁群最终位置分布图和最优函数值变化图像，输出最优的位置坐标。

3 实例验证

3.1 算法实例仿真验证

由于货位分配的侧重点不同会导致分配结果的不同，因此，通过层次分析法 （AHP）的计算并综合考虑立体仓库的实际情况[10]，取μ1=0.432，μ2=0.292，μ3=0.276。以某高校减速箱加工小产线的自动化立体仓库货位分配任务为例。采用Python语言进行仿真验证，立体仓库的各项参数如表1所示。

表1 自动化立体仓库基本参数Table 1 Basic parameters of automatic stereo warehouse

现有14件加工的物料，已知各个物料的质量以及加工次序，如表2所示。

表2 货物实例信息Table 2 Goods instance information

针对此次货位分配任务，采用ACO算法和IACO算法分别进行优化。研究参数的初始设置对蚁群算法性能的影响，并且分析了如何就参数的初始设置可以进一步改善其性能。算法的参数如表3所示。

表3 算法参数Table 3 Algorithm parameters

根据建立的自动化立体仓库货位分配模型并结合 ACO及 IACO 算法对该货位分配任务进行优化求解，其目标函数随迭代次数的变化如图4所示。

目标函数优化是求解其最小值问题，从图4可以看出，随着迭代次数的不断增加，目标函数值在不断逼近函数的最小值，说明其解是逐步趋近最优解的。相比ACO算法，IACO算法明显收敛速度更快，在31代达到最优，此时函数值为1.5484，ACO算法在52代左右达到最优，函数值为1.6215。可见 IACO相比ACO 算法效率明显提高，并且经过多次试验，IACO比ACO算法稳定性更高，证明了IACO算法的有效性和优越性。

图4 目标函数随迭代次数的变化Fig.4 Variations of objective function with number of iterations

ACO算法和IACO算法优化后的货位坐标分别如表4和5所示。根据试验设定要求和具体情况可知，按照货位分配优化原则，IACO优化结果更符合规则设定，证明了IACO算法的可行性。

表4 ACO算法优化后的货位分配信息Table 4 Location allocation information optimized by ACO algorithm

表5 IACO算法优化后的货位分配信息Table 5 Location allocation information optimized by IACO algorithm

3.2 数字孪生系统验证

基于可适应性规划仿真平台构建数字孪生系统原型 （图5）。原型包括7个模块，即基本数字地面系统、3D半物理建模、半物理示教程序、二维图纸规划、开源化软件助手、信号连通性和可适应规划。基于提出的关键技术，性能模块分析采用Python编程架构开发，并与联合优化模型集成。一旦演示程序接收到货物信息，将调动对应模块快速执行优化，然后将优化结果传输到半物理仿真模块进行编码并计算出各个运动轴的具体移动距离。3D半物理建模模块可以给模型建立真实的物理属性来描述实际的物流和库存过程。仿真运行过程中将来自物理系统的原始数据反馈到多视图同步模块，用于与其他系统协调。

图5 基于可适应性规划仿真平台的数字孪生系统原型Fig.5 Digital twin system prototype based on adaptive planning and simulation platform

利用产线网络布局、计算机信息技术搭建试验布局，运用数字孪生技术构建虚实同步的仿真平台，使得设备与其数字孪生仿真模型实现实时通信与动作同步。 建立立体仓库数字孪生仿真模型的Python脚本与自动化立体仓库数控系统之间的虚实同步通信通道，实现自动化立体仓库物理模型实时数据与数字孪生仿真模型数据的实时同步，进而实现自动化立体仓库数字化模型、立体仓库实物系统之间的动作同步，相比普通产线，集成数据化管理与控制的智能化生产线能有效依托数据化应用能力，提高产品加工效率。由图6可知，普通智能生产线每加工一件成品需要3.5 h，则生产5件成品需要17.5 h，结合数字孪生的智能生产线生产成品所用时间逐件减少，生产5件成品需要16.2 h，较普通智能生产线提高7.4%。证明了该方法能够满足立体仓库基于工艺的物料出入库智能选择货位需求，在智能生产线上的应用对提高航空航天设备生产模式的智能化程度具有重要意义。

图6 两种生产线生产成品数量与所用时间对比Fig.6 Comparison of number of finished products between two production lines

4 结论

本文针对智能生产线中的自动化立体仓库货位分配智能化低的问题，研究了一种快速稳定的改进启发式蚁群算法。采用数字孪生体多维度融合建模方法构建自动化立体仓库数字孪生多维模型，搭建智能生产线数字孪生系统架构，建立了以工艺排产次序、货品相关性、货架稳定性为目标的数学模型，得出了改进的启发式蚁群算法的收敛迭代次数和优化后的货位坐标，结果表明，改进的启发式蚁群算法适合求解智能生产线自动化立体仓库货位分配目标优化问题。将优化后的货位分配信息集成到数字孪生系统中加以验证，得出智能生产线较普通智能生产线的生产效率提高7.4%。由此可见，该方法能够满足自动化立体仓库货位智能分配需求，对航空航天产品实现智能制造、提质增效具有重要意义。