冷弯薄壁型钢-OSB双向板组合楼盖试验研究
2023-03-15章宇川曹宝珠王洗凡游智越
章宇川, 曹宝珠, 王洗凡, 游智越
(海南大学土木建筑工程学院,海口 570228)
木材作为一种可再生的建筑材料,具有保温隔热、轻质高强、抗震耐久等诸多优点,是中国建筑业中使用较早的建筑材料之一[1-2]。但是木材属于各向异性材料并存在木节、斜纹理以及因生长应力或自然损伤而形成的缺陷,且在组合形式的建筑中,不借助其他材料的情况下不能很好地传递拉力[3]。在20世纪末期,定向结构刨花板(oriented strand board,OSB)作为一种新型建筑材料因其具有更良好的握钉能力,更高的抗弯强度且线膨胀系数更小,同时也具有保温隔热、生命周期能耗低等环保特性[4-5]得到迅速发展应用。同时钢结构具有质量轻强度高、延展性好、材质均匀、符合力学假定等优点,在建筑中被广泛应用,但是与其他建筑材料相比,在承载能力相同的情况下钢结构的截面积更小,更容易发生失稳破坏[6]。如果将传统钢结构与传统木结构通过某种组合方式使其形成一个钢木组合结构,此组合结构在一定程度上能够克服钢结构与木结构的缺点,并且还能够发挥钢结构与木结构各自的优点;木材能够为组合结构提供侧向支撑,防止钢材因屈曲变形而过早导致失稳破坏,使得组合结构承载力相较于纯钢或纯木结构有着大幅提高[7-9]。将冷弯薄壁型钢和OSB板组合形成一种新型的钢木组合结构体系,其具有轻质高强,绿色环保等优点,具有较大的实际意义[10]。
目前,冷弯薄壁型钢住宅结构体系已基本完善[11]。管宇等[12]已对多层冷弯薄壁型钢结构住宅水平荷载分配进行研究,并对不同构造组合楼盖刚性的判定方法提供了科学依据。许操[13]研究了拼合大截面冷弯薄壁型钢梁受弯性能。姚宇航等[14]对冷弯薄壁型钢-胶合木组合梁受弯性能进行了有限元分析。但是对于冷弯薄壁型钢-OSB板组合双向板楼盖结构的试验研究却鲜有报道。楼盖作为楼层分隔构件不仅传递各种竖向荷载,而且起到连接各个承重结构的作用[15]。为此,研究冷弯薄壁型钢-OSB板组合双向板楼盖在均布荷载作用下的受力情况以及它的抗弯承载能力。为能更好地将冷弯薄壁型钢-OSB双向板组合楼盖应用到实际工程提供了科学依据。
1 试验概况
1.1 试件设计
为了研究冷弯薄壁型钢-OSB组合双向楼盖的抗弯承载能力,试验设计制作了一块尺寸为3 700 mm×3 700 mm的足尺试件,对其进行单调静力堆载实验。作为一种新型的双向受力组合楼盖,其主要组成部分包括:楼面板(OSB板)、组合承重梁(OSB板、冷弯薄壁型钢)、肋板(OSB板)、角钢和螺钉等。图1为试件示意图。图2为试件大样图。

图1 试件示意图
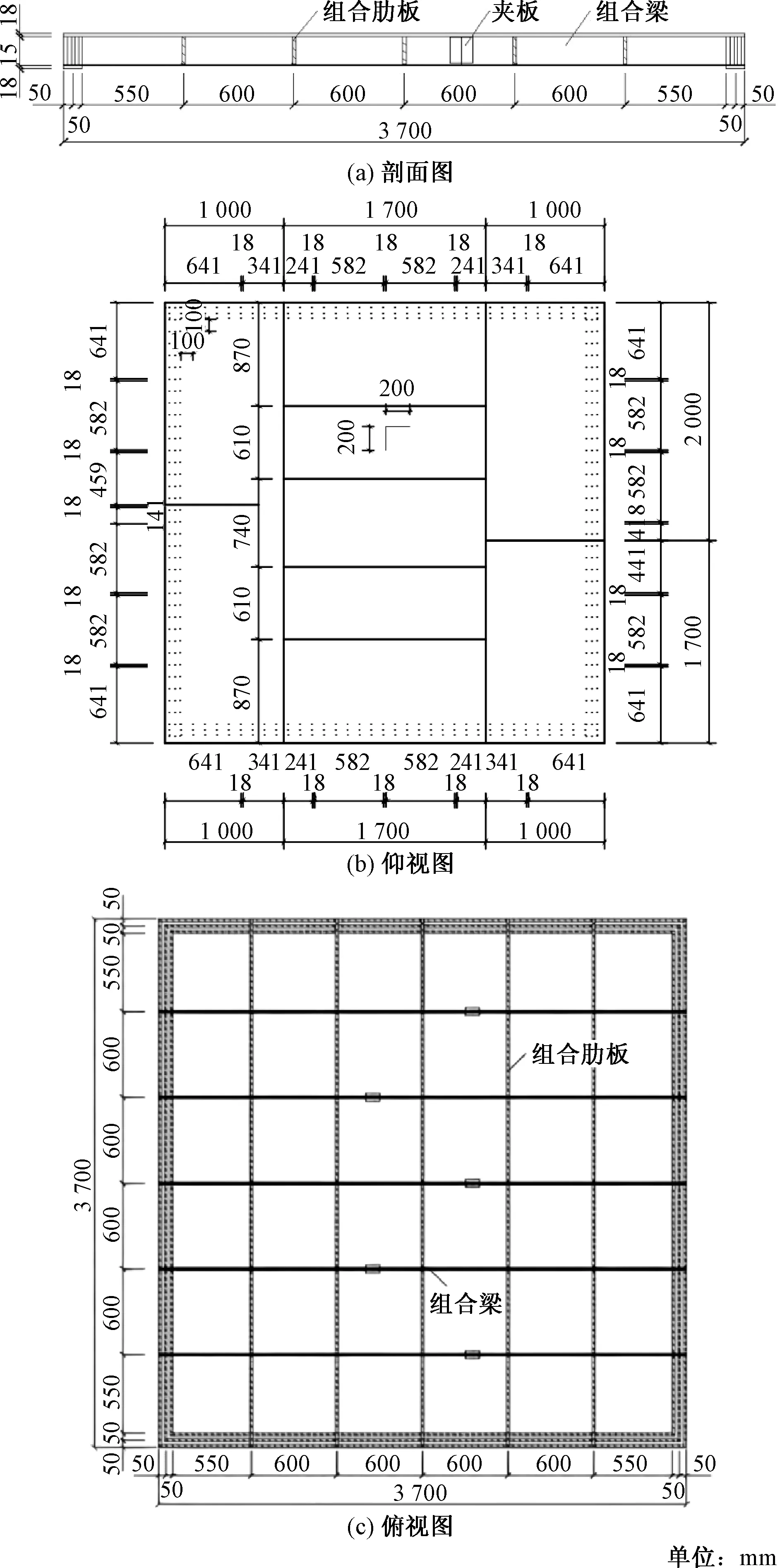
图2 试件大样图
(1)楼面板。使用9块厚度为18 mm的OSB板组合而成,每根组合梁间距都为600 mm,经拼接组合后的楼面尺寸为3 700 mm×3 700 mm,并在边缘肋板的凸起位置预留凹槽。
(2)组合承重梁。由5组长度分别为2 200、1 500 mm,高度150 mm,厚度18 mm的OSB定向结刨花板通过夹板与T型直钉连接形成,组合后的承重梁长度为3 700 mm。夹板的尺寸为140 mm(高)×120 mm(宽)×18 mm(厚),每根OSB板梁下部采用1 mm厚的冷弯薄壁型钢通过自攻螺钉连接与其形成组合梁,并且为了减小钢板的初始弯曲,将钢板沿宽度方向弯曲成腹板高度为18 mm、翼缘宽度为5 mm的U型钢条。
(3)组合肋板。为了保证组合楼盖的整体性并使其能够双向受力,将肋板沿承重梁垂直方向布置,使用T型直钉进行连接,肋板间距为600 mm。在肋板底部组合有厚度为1 mm,长度为3 700 mm的U型冷弯薄壁型钢以增强其整体性。
(4)角钢。为了加强肋板与承重梁的连接,在每个肋板与承重梁的连接处设置4个角钢进行连接。并且为了防止钢板在梁端部的滑移,在端部设置槽型钢板,加强钢板与梁端的联结性。试验中采用的自攻螺钉直径均为5 mm,但在不同位置的螺钉间距与长度有所不同,具体数据如表1所示。
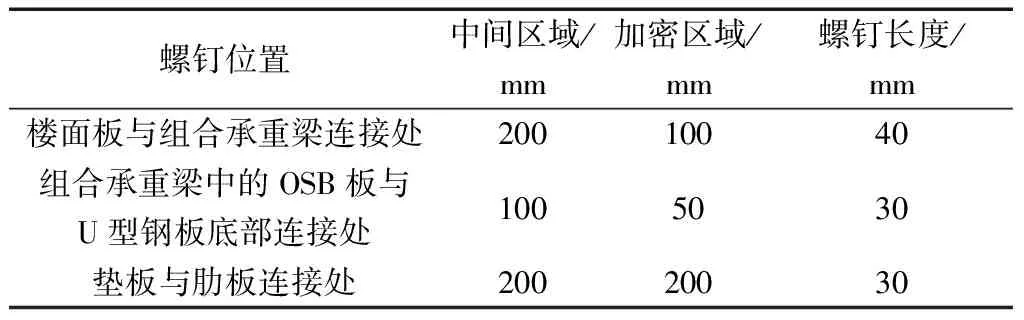
表1 螺钉间距和螺钉长度
1.2 材料性能
本试验构件中使用的冷弯薄壁型钢均采用厚度为1 mm的优质国产高强度奥氏体不锈钢,型号为s30408,材性试验所用的3块试件与组合楼盖构件中使用的钢材为同一批次。钢材的材性试验根据《金属材料拉伸试验 第1部分:室温试验方法》(GB/T 228.1—2010)[16]与《金属材料弹性模量和泊松比试验方法》(GB/T 22315—2008)[17]进行试件设计。经实测,钢材的屈服强度为267 N/mm2,抗拉强度为702 N/mm2,弹性模量为135 410 MPa,泊松比为0.3。OSB板静曲强度平均值为34.1 MPa(平行方向)、21.5 MPa(垂直方向)。
1.3 试验装置
本组合楼盖静力试验在土木结构试验室完成,试件制作完成后用吊车将其吊运至实验室内的砖墙上。试验装置包括方形砖墙、圆钢滚轴、钢垫板等,试验装置如图3所示。方形砖墙四边尺寸为3 700 mm×3 700 mm,厚度为100 mm,墙体高度为1 000 mm,方墙中部留有门洞,主要用于完成粘贴应变片、焊接导线、安装百分表、试验加载过程中观察试件变形、试验结束后分析试件破坏特征等工作。该组合楼盖边界条件为四边简支,楼盖支座处放置钢垫板与圆钢,圆钢置于上下钢垫板中轴处并采用木楔进行固定,使其形成四边简支结构。
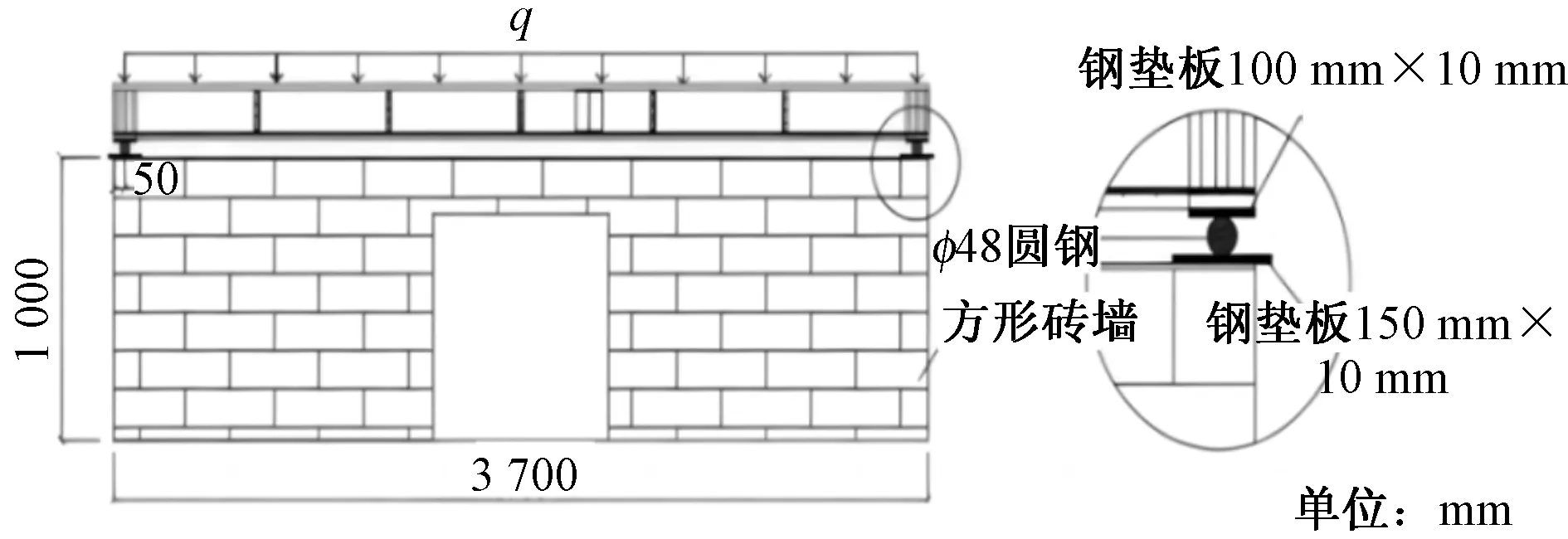
q为均布荷载
1.4 测点布置
在钢板底部(1~10号)四端支座处对应的OSB楼面板(11~18号)与组合楼盖跨中处(19~22号)布置位移传感器,以测得试件在均布荷载作用下各特征点的位移。测点位置如图4所示。
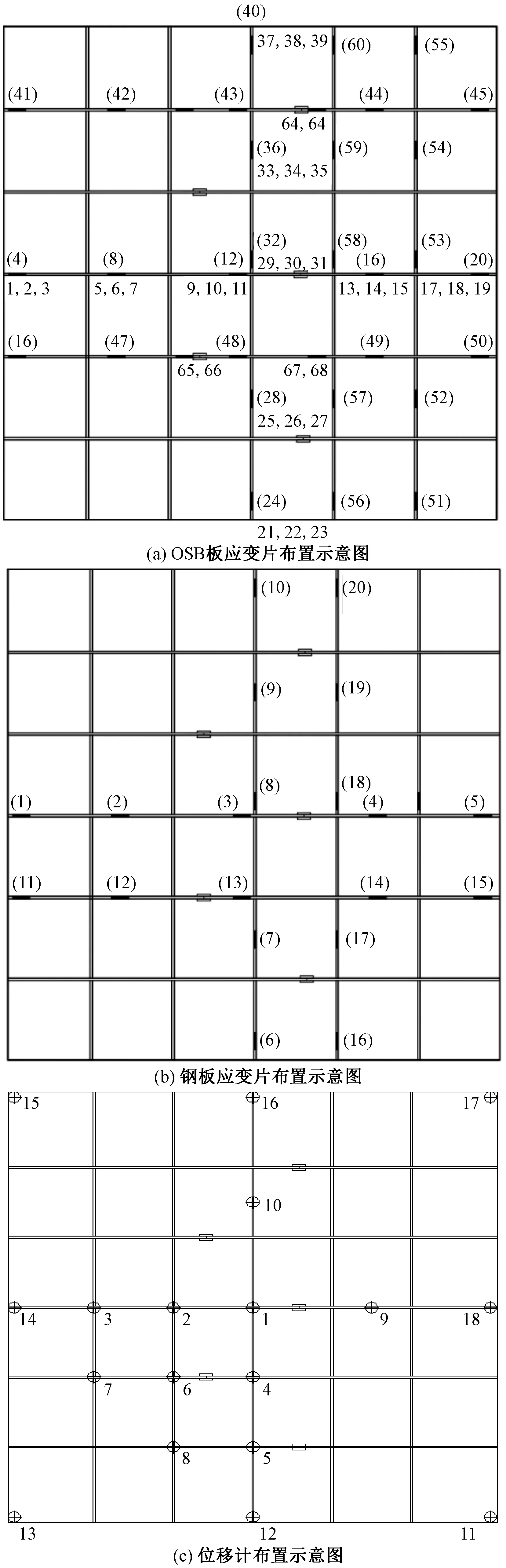
带()的数学为应变片,其他数字为位移计编号
1.5 加载制度
试验正式加载前,对组合楼盖试件进行预加载,预加载时将荷载预加至0.81 kN/m,即加载物重为1.08 t。因为构件制作安装时各部件连接不够紧密,存在缝隙等情况,所以通过预加载使各部件有更好的结合状态,并且在预加载过程中,楼盖无明显变形,各仪器工作状态良好,卸载后平衡归零,随后进行正式加载。
正式加载采用分级加载,每级为0.27 kN/m2,即每级加载物重量为0.36 t,并且当楼盖跨中挠度达到l0/200时,即位移达到18 mm时,将每级荷载降低至0.14 kN/m,即每级加载物重量为0.18 t,其中l0为跨度。
2 试验结果及其分析
2.1 试验过程及实验现象
当试件跨中挠度达到l0/50,即跨中位移达72 mm时,组合楼盖达到承载能力极限状态,试件视为破坏。试件达到破坏时,试件累计加载值为3.94 kN/m2,试件累计加载荷载值为51.16 kN(图5)。加载时,由人工将重物吊运至楼盖之上,并由从中间到四周的顺序放置,试件达到破坏时,楼盖上所施加荷载近似为均布荷载。

图5 试件加载图
当结构达到承载力极限状态时,观察各测点位移荷载数据,可以看出组合楼盖变形依旧呈线弹性状态。在对组合楼盖试件进行静力加载至破坏的全过程中,试件无明显破坏,组合承重梁未出现裂缝,楼面板与组合梁间未出现相对滑移,说明楼面板与组合梁连接紧密,能够实现共同工作,组合楼盖试件表现良好。
2.2 荷载-位移曲线
图6为组合楼盖试件的荷载-挠度(P-Δ)曲线,可以看出,加载初期各测点的P-Δ曲线均呈线性增长。当试件加载至31.75 kN,即楼面荷载达到2.43 kN/m2时,曲线出现拐点,斜率减小,位移增长速率变大,呈现非线性变化,此时组合楼盖进入弹塑性状态。由于组合楼盖各部分采用螺钉连接,螺钉在挤压下易发生变形,因此曲线出现非线性主要是由于楼盖拼接处发生相对变形所致;沿x轴方向与沿y轴方向的曲线斜率基本相同,当竖向位移达到72 mm,此时楼面荷载为3.94 kN/m2,认为此时的组合楼盖试件达到承载能力极限状态,视为构件已经破坏,冷弯薄壁型钢-OSB组合楼板承载能力由挠度控制。
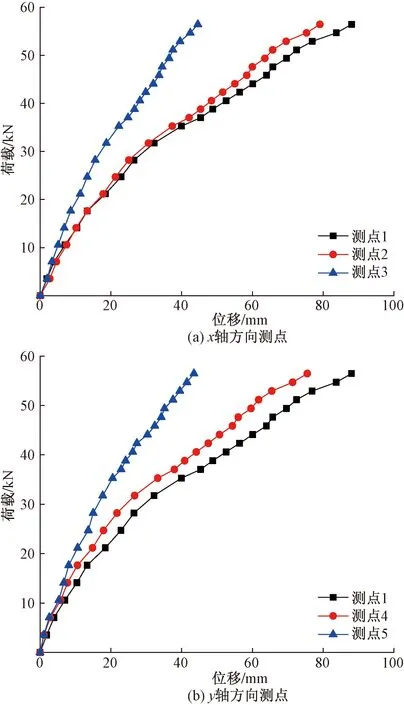
图6 荷载-位移曲线
2.3 荷载-应变曲线
图7、图8为组合楼盖的荷载-应变曲线。其中x为OSB梁腹板下部应变与钢板下部表面应变。可以看出,在楼板跨中处随着荷载增加OSB梁腹板与钢板应变增速最快,且向两端递减。并且沿x轴与沿y轴方向曲线变化情况基本一致,说明该冷弯薄壁型钢-OSB组合楼盖双向受力性能良好。
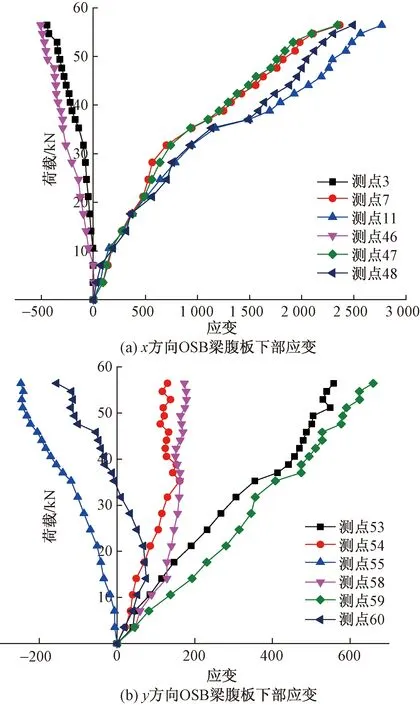
图7 OSB梁腹板荷载-应变曲线
从图8中可以看出,钢板变形主要集中在中间区域,楼盖试件在达到破坏条件时底部钢板已达到屈服,并且钢板下表面沿y轴方向应变值略大于沿x轴方向的应变,由于沿y方向的钢板是通过自攻螺钉固定在轴钢板下侧,因此y轴方向应变会大于x轴方向的应变。
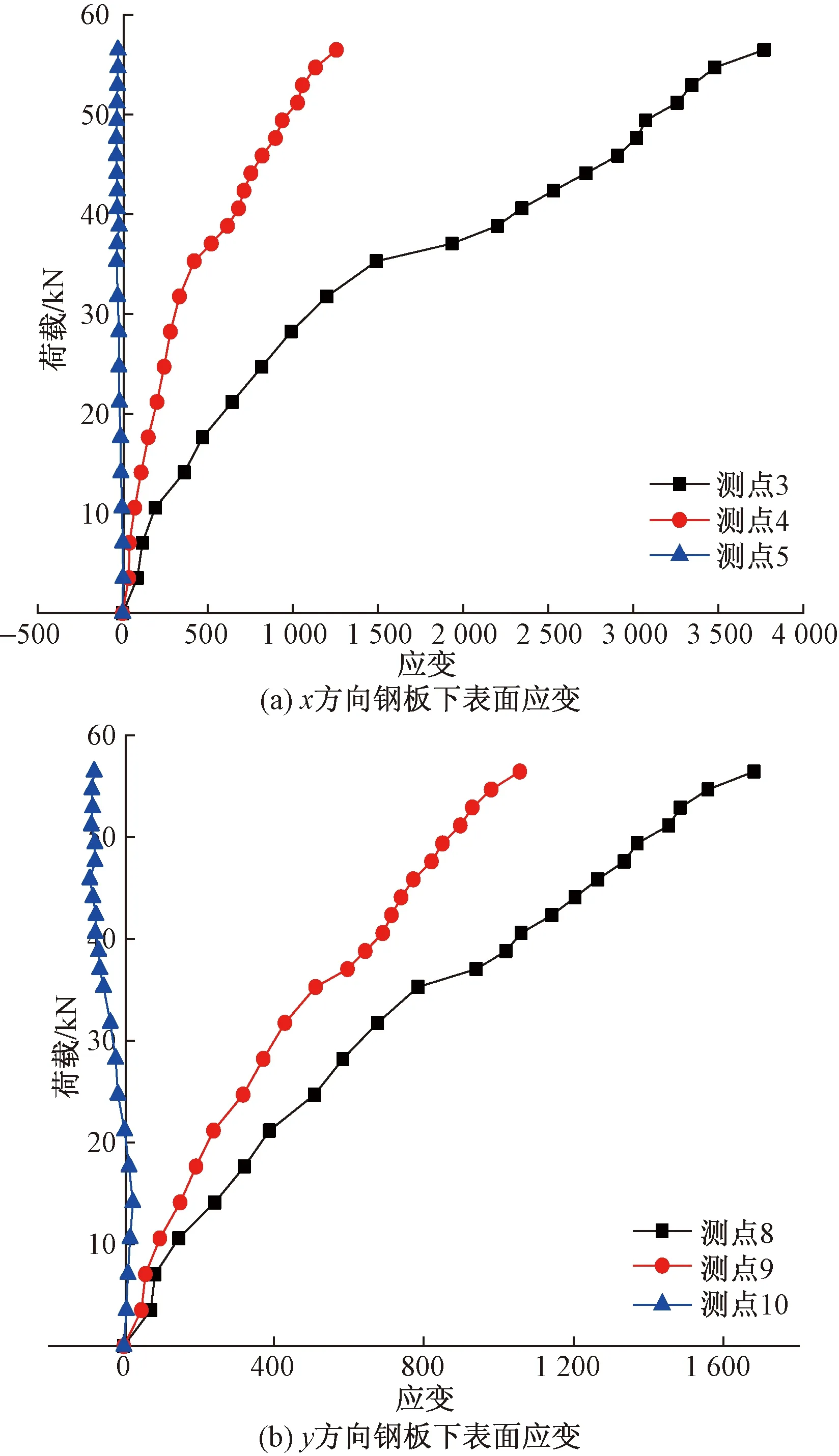
图8 钢板荷载-应变曲线
2.4 平截面假定验证
图9为组合楼盖跨中截面纵向应变在不同荷载下沿截面高度的分布情况,截面包括5个测点,分别位于楼面板上表面、OSB梁上、中、下部与钢板下表面。将材料受压时所得的应变记为负值,受拉时所得的应变记作正值;纵坐标表示测点距底部钢板下表面间的距离。可以看出,在试件加载初期荷载较小时,楼盖的纵向应变沿截面高度的分布呈线性关系,此时符合平截面假定原理。但随着荷载的增加,由于x轴方向承重梁为非贯通梁,导致了梁拼接处出现了相对偏移,变形增大。且OSB楼面板在支座处虽未产生滑移,但在跨中处与组合梁发生了相对滑移,故当荷载较大时构件各截面将不符合平截面假定。从图9中还可以看出,下部钢板应变相比于OSB梁腹板更大。
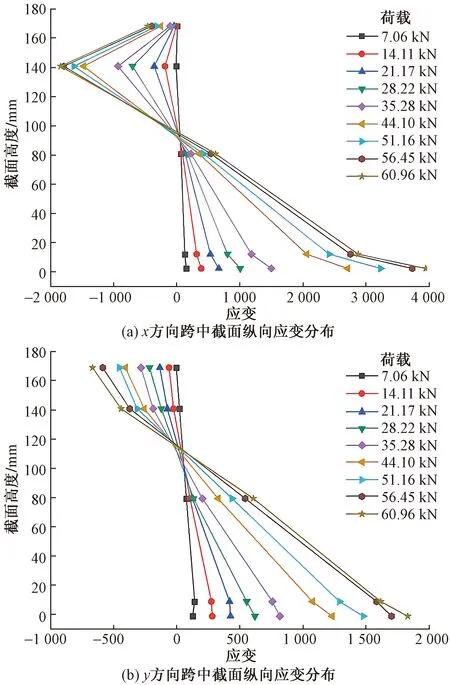
图9 跨中截面应变分布
3 有限元分析
3.1 有限元模型建立与验证
基于ABAQUS有限元软件建立了冷弯薄壁型钢-OSB板双向组合楼盖的有限元分析模型,分别采用S4R5薄壳单元和C3D8R实体单元模拟冷弯薄壁型钢与OSB板。为了使组合楼盖的受力情况更加贴合实验值,对模型所施加荷载及边界条件进行定义。首先本试验采用沙袋堆载的方式对试件施加均布荷载,在有限元分析时,在OSB楼板上方施加垂直与楼面板的均布荷载;根据组合楼盖试验的实际安装过程,组合楼盖模型的边界条件定义为简支边界,约束其x、y、z方向的平动自由度,但不限制平面内的转动自由度。在试验加载过程中,试件与钢垫板、OSB垫板间处于静摩擦状态,故楼盖试件与钢垫板,OSB垫板间采用绑定约束;自攻螺钉采用嵌入约束与模型连接;楼面板、梁与肋板间的连接采用摩擦接触单元。
试件的有限元模拟分析与试验的P-Δ曲线比较如图10所示。有限元模型在前期荷载作用下,位移随着荷载的增大而增大,当荷载达到31.57 kN时,荷载-位移曲线出现拐点,曲线斜率略微降低,荷载增长速率逐渐减小,试件进入弹塑性阶段。从图10中可以看出,当荷载值均达到51.16 kN时,有限元分析结果比试验结果的跨中竖向位移低20.35%;在跨中挠度均达到72 mm时有限元模拟得出的结果相较于试验的极限荷载更大。可见,通过有限元模拟得出的极限荷载相较于试验得出的更大。由于试件切割组装时不可避免存在误差,且螺钉在钻入钢板与OSB板等的过程中无法保证完全垂直,故有限元模拟结果与试验结果存在一定误差,但二者的P-Δ曲线基本吻合,极限承载能力接近,总的来说模拟结果与试验结果吻合较好。
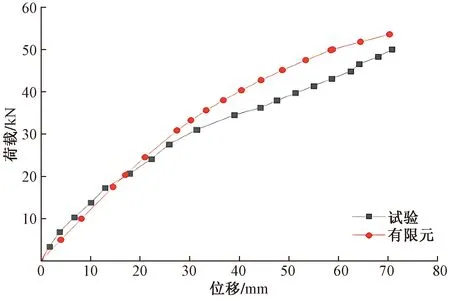
图10 模拟与试验P-Δ曲线对比
3.2 有限元变参数分析
为分析各种参数对冷弯薄壁型钢-OSB板组合楼盖的影响,采用上述有限元模型通过单一变量法分别改变OSB梁腹板高度、冷弯薄壁型钢板厚度与螺钉间距,以此来分析这几种参数对组合楼盖承载力的影响。
3.3 OSB梁腹板高度对组合楼盖承载力影响
图11为在不同梁腹板高度情况下,楼盖试件跨中的P-Δ图,可以看出,增加梁腹板高度能够明显提高楼盖承载能力,当高度由130 mm增加至150、180 mm时,组合楼盖的极限承载力从47.40 kN分别提升至54.79、64.83 kN,荷载增加幅值为15.6%与33.6%。说明增加梁腹板高度能够有效地提升楼盖的极限承载能力。

图11 不同OSB梁腹板高度下的荷载-位移曲线
3.4 冷弯薄壁型钢板厚度对组合楼盖承载力影响
图12为在不同钢板厚度条件下楼盖试件跨中的P-Δ图,钢板厚度分别为0.5、1、2 mm。可以看出,在加载前期随着钢板厚度的增加,荷载-位移曲线的斜率也在增加。随着钢板厚度从0.5 mm增加到1 mm与2 mm时,组合楼盖的承载能力分别提高了7.5%、21.8%,相应的跨中挠度略有增加,但承载能力有较好的改善。由此可见,在保证钢板与楼盖结构协同工作的情况下,增加钢板的厚度能够有效提高组合楼盖的承载能力。
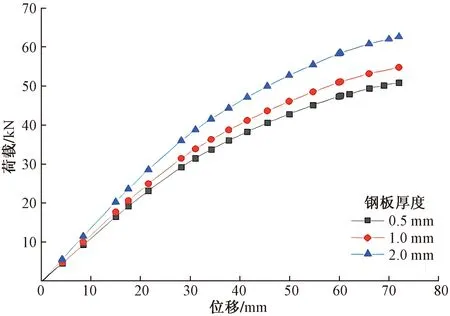
图12 不同钢板厚度下的荷载-位移曲线
3.5 螺钉间距对组合楼盖承载力影响
为分析螺钉间距对组合楼盖承载能力的影响,模型中分别采用100/200(表示组合梁端部螺钉间距100 mm非端部的螺钉间距200 mm)与50/100两种组合,所得的跨中的P-Δ曲线如图13所示。可以看出,两个模型的曲线几乎重合,随着螺钉间距的减小,组合楼盖的承载力并没有明显提高,当螺钉间距从100/200缩小至50/100时,楼盖跨中竖向位移仅仅减少了1.82 mm(3%),承载力只提升了1.55 kN(2.9%)。说明较小螺钉间距并不能对较好的改善梁的受力性能,提高其承载能力。

图13 不同螺钉间距下的荷载-位移曲线
4 结论
通过对足尺冷弯薄壁型钢-OSB板双向楼盖进行单调静力堆载试验,研究冷弯薄壁型钢与OSB板通过自攻螺钉连接组合成的双向楼盖在荷载作用下的力学性能,研究双向组合楼盖各材料的协同工作能力,并通过ABAQUS建立有限元模型,改变构件参数来分析OSB梁腹板高度、冷弯薄壁型钢板厚度与螺钉间距对楼盖承载能力的影响。得出如下结论。
(1)该冷弯薄壁型钢-OSB板双向楼盖具有良好的承载能力,能够满足普通住宅对于楼盖承载力的需求。
(2)组合楼盖的破坏均表现为跨中挠度达到了破坏标准,OSB承重梁并没有出现较大裂缝,该楼盖延性较好。
(3)在加载过程中,组合承重梁OSB腹板与钢板的纵向应变基本成线性分布,冷弯薄壁型钢与OSB两种材料能够很好地协同工作,共同受力。组合承重梁各截面上纵向应变和截面高度基本呈线性变化,符合平截面假定原理。
(4)在组合楼盖加载全过程中,试件并未出现明显破坏现象,组合承重梁未出现裂缝,OSB楼面板与组合梁端也为出现相对偏移。在X轴与Y轴方向P-Δ曲线基本一致,说明该组合楼盖双向受力性能良好。
(5)通过ABAQUS进行有限元分析,并将分析结果与试验结果进行对照,有限元结果与试验结果吻合较好,研究不同影响因素对组合楼盖跨中挠度和抗弯承载力的影响,结果表明增大OSB梁腹板高度、增大钢板厚度、减小螺钉间距均可以提高组合楼盖的抗弯承载能力。
