含球形相变胶囊的混合储能水箱特性模拟研究
2023-03-15王凌皓刘方
王凌皓,刘方
(上海电力大学能源与机械工程学院,上海 201306)
随着氢能、海洋能、生物能等绿色能源的发展与使用,全球对煤炭等对环境造成污染的能源的需求每一年都在降低,空气质量得到一定的改善[1]。近年来,氢能,生物能等可再生绿色能源对资源短缺以及环境污染的问题解决有很大帮助,而绿色能源的储存手段是提高这些绿色能源利用率的关键[2-4]。为了提高绿色能源的使用率,降低碳化合物的排放量,保护环境。相变储能技术作为有效的储能手段,受到中外学者的广泛重视[5-7]。人们越来越致力于储热方面的研究,在不同的能源利用和转换系统中,蓄热装置的蓄热和放热特性可用于解决时间和空间上的供需矛盾,因此开发一种新型蓄热装置很有必要[8-9]。
吴璠等[10]分析了相变水箱在不同相变墙体厚度下蓄放热过程以及相变墙体对其的影响。余妍等[11]对相变储热罐内换热管的结构进行了优化,设计了含相变储热罐的CO2喷射式热泵系统。丁志雄等[12]将相变材料(phase change meterial,PCM)-水联合储能应用到太阳能热水系统中,得知PCM相变温度及体积比的选择对水箱的性 能有很大的影响。陈亚飞[13]采用圆柱型相变材料,空气为换热流体并使用了3种熔点为317、326、337的商业石蜡,结果表明相变性能的提升与PCM种类的多少成正比。Talmatsky等[14]使用熔融温度为50 ℃ PCM可使所需的备用电热减少2倍。PCM的加入可提高收集器的效率。华维三等[15]研究发现,在太阳能集成器的相变储能系统中,由于圆柱型相变材料与水箱内相变流体的温度差,在圆柱型相变单元外增加金属肋条可增加有效传热面积,有利于整个相变储能系统效率的提高。Wright等[16]研究了将PCM放置在热分层储罐顶部的效果,除罐顶层冷却时间的大幅延迟外,还可显著提高储存容量,结果表明:只要仔细优化PCM的设计参数,如熔化温度范围和熔化潜热,排放水的冷却时间可以缩短2倍。Reddy等[17]研究了充电时质量流量对球形容器中封装不同PCM的太阳能热存储系统充电速率的影响,发现质量流量增加3倍可使熔化时间缩短约23%,这是由于质量流量对传热流体(heat transfer fluids,HTF)和PCM之间的传热系数的影响。以上研究对储能水箱内部加热过程中的热分层特性影响机理的研究仍有一些空缺,因此需要对此展开更进一步的研究。
为此,通过对蓄热水箱的模拟研究,研究蓄热水箱在不同入口流量、不同相变单元尺寸以及相变单元距离水箱底部高度的不同工况下的热分层模拟情况,并对其内部的影响机理进行研究。利用平均蓄热率、蓄热密度、理查德森数等储能指标分析模拟储能水箱的储能效果,通过与前人研究的模拟结果对比验证所建立模型的准确性,为后续的蓄热水箱的相变模拟研究提供理论依据。
1 数值模拟
1.1 物理模型
所建立的储能水箱模型为上进下出的进出口模式,传热流体从水箱上部流入装置内,与水箱内球形相变胶囊进行传热后由水箱底部流出。在 ANSYS workbench中进行模型的创建以及网格划分,采用非结构化网格,并对水箱的出入口以及PCM区域网格进行加密处理。建立物理模型如图1所示。为了简化模型,假设球形相变胶囊之间没有接触,并且假设球形壁面具有足够的弹性不会在相变材料熔化体积膨胀时发生破坏。在理想模型上对相变球形胶囊的单元尺寸,摆放高度以及入口流速进行了数值模拟分析。PCM的物性参数如表1所示。

L为水箱高度;D为水箱直径;x为流体随时间流动的长度变化;h为胶囊随时间的高度变化

表1 相变蓄热胶囊的物性参数
1.2 数学模型
所建立的数学模型分为两个区域:一个是传热流体的流动区域,另一个是相变胶囊的封装PCM区域,基本控制方程分为能量守恒方程、质量守恒方程和动量守恒方程。
传热流体流动区域控制方程如下。
(1)能量守恒方程。

(1)
式(1)中:t为流体流动传热时间;cp为比热容;k为热传导率;ST为热源强度。
(2)动量守恒方程。

ρrefβ(T-Tref)g
(2)
式(2)中:∇为梯度算子;τ为黏性应力张量;g为重力加速度;ρ为流体密度;ρref为流体参考温度;T为流体温度;Tref为流体参考温度;β为液化率。
(3)质量守恒方程。
∇u=0
(3)
式(3)中:u为某一任意点的速度。
相变材料在水箱内的蓄热过程可分为3个阶段,PCM各阶段的能量方程如下。
固态显热储能过程可表示为

(4)
式(4)中:Cp,s为相变胶囊的比热容。
储热阶段过程可表示为

(5)
式(5)中:Hm为融化焓。
液化率β在0~1变化,可表示为
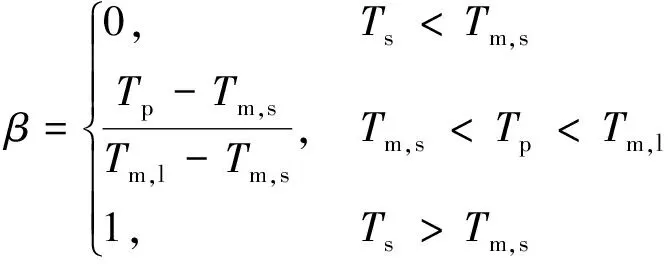
(6)
式中:Tm,s为相变材料维持固体温度;Tm,l为相变材料液化温度;Tf为传热流体温度;Tp为PCM胶囊温度;hv为相变胶囊的传热系数;ks为PCM固相热导率;kl为PCM液相热导率;ρs为PCM固相密度;ρl为PCM液相密度。
液态显热热能储存阶段可表示为
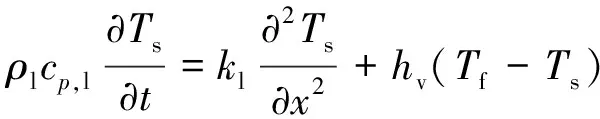
(7)
式(7)中:cp,l为PCM液相比热容。
采用水作为传热流体,水的物性参数很大程度影响了其在水箱内部与相变材料的换热,因此需要引入更正公式对水的物性参数进行更正。
密度的计算公式为
ρ=(999.839 52+16.945 17t-
7.987 040 1×10-3t2-46.170 461×10-6t3+
105.563 02×10-9t4+
280.542 53×10-12t5)/(1+
16.879 85×10-3t)
(8)
比热的计算公式为
Cp=4.185 5×[0.996 185+
0.011 16×10-0.036t]
(9)
1.3 求解参数设置
建立储能水箱结构参数由表2所示。将网格划分完成的模型导入FLUENT进行模拟,模拟在无量纲时间达到1时水箱内的变化,此时水箱内完全充满换热流体,并且发生了相变的过程,模型内的水箱竖直放置,竖直向下的重力加速度为9.8 m2/s,边界条件如表3所示,采用湍流模型进行模拟计算,采用等效热容法对数值模型进行求解,使用 SIMPLE 算法对速度和压力进行耦合求解,采用PRESTO!格式离散压力项的差值,迭代收敛残差均设置为小于10-6。

表2 水箱装置结构参数

表3 边界条件设置
2 水箱热特性计算模型
2.1 无量纲时间
通过定义无量纲时间[18]可以对不同工况下的水箱在其分别对应的时间内的蓄热能力进行比较,无量纲时间τ定义为

(10)

(11)
式中:t为传热流体流动的时间;t0为水箱内部完全被传热流体换热所需时间;VT为水箱的有效体积;q为流入水箱的质量流量。
2.2 平均蓄热率与蓄热密度
储能水箱的实际储能水平是通过其相变材料吸收传热流体内部热能的能力进行评价的,选择储热密度与平均蓄热率两个指标进行评价[19],储热密度ρcharge与平均蓄热率Pcharge计算公式分别为

(12)
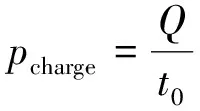
(13)
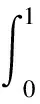
(14)
式中:Q为水箱蓄热总量;VT为水箱有效体积;cp,f为传热流体比热容;q为质量流量;Ttop为水箱入口温度;Tbottom为水箱出口温度。
2.3 理查德森数
理查德森数Ri表示浮力和流剪切力的比值的无量纲数[20-21],可以用来表征储能水箱内热分层的效果,理查德森数越大,水箱内热分层效果越明显。

(15)
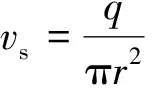
(16)
式中:g为重力加速度;ε为膨胀系数;H为水箱高度;vs为进入水箱平均流速;r为水箱入口当量半径。
3 实验结果与分析
3.1 网格无关性验证
网格数量对于模拟精度起到一定作用,采用非结构化网格,所建立网格数量为42×104、82×104、120×104。图2为不同网格数量的情况下水箱出口温度随无量纲时间的变化趋势,结果表明:网格数为42×104时与网格数为82×104、120×104相差为0.02%与0.06%,计算精度并未随着网格数增加而增加,但随着网格数增加,计算所需要的条件更加烦琐,因此选用42×104的模型来计算。
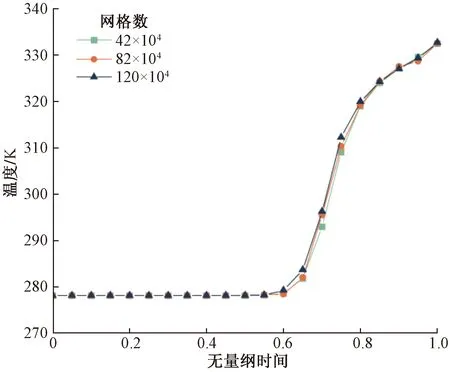
图2 网格数量无关性验证
3.2 时间步长无关性验证
测试了时间步长分别为0.1、0.2、0.3 s时水箱出口温度在相变换热过程中的变化情况,如图3所示,结果表明:时间步长为0.1 s时与时间步长为0.2 s和0.3 s时相差0.16%与0.2%,考虑到计算中所节省时间,选用时间步长为0.1 s作为本模型的模拟。
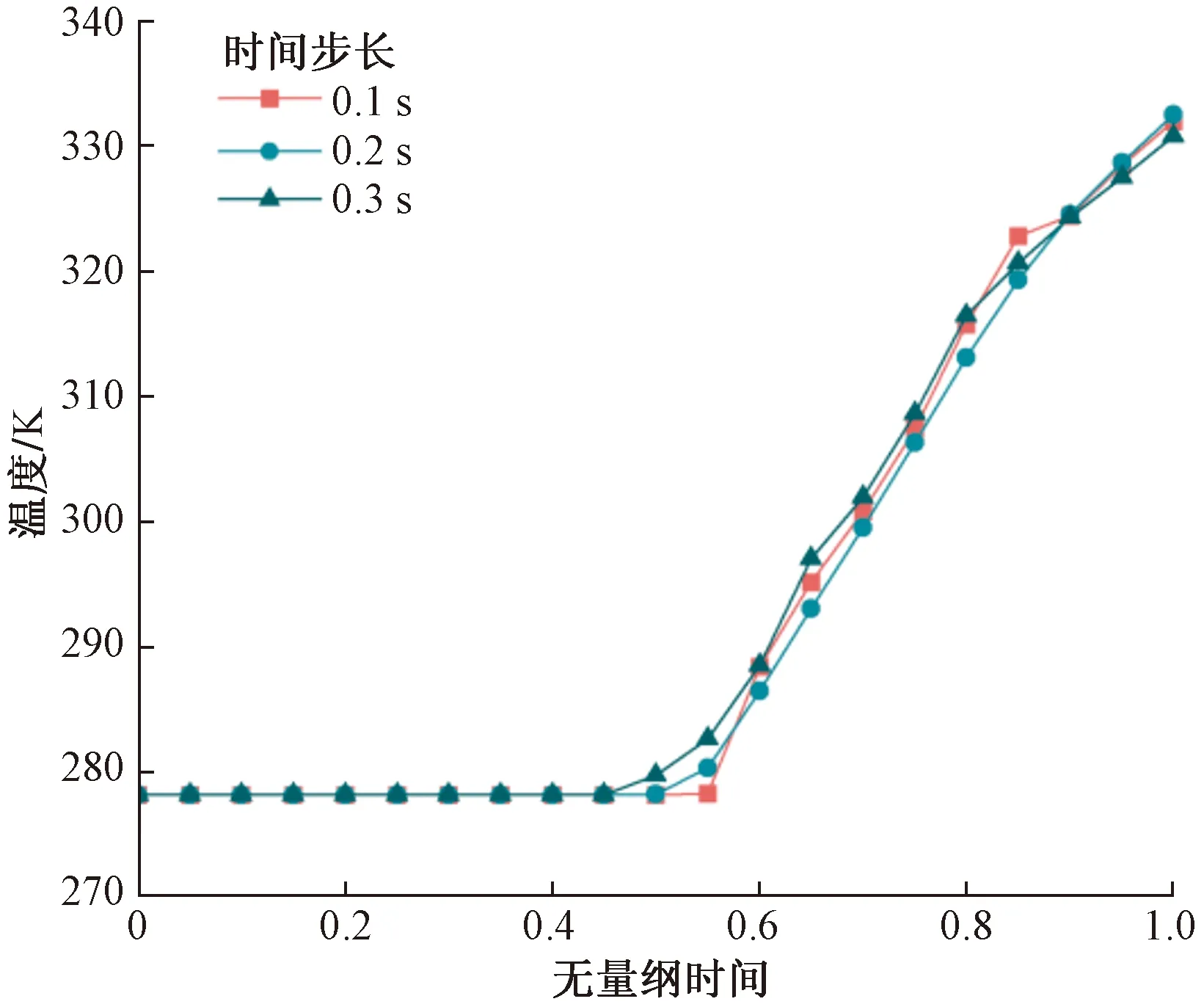
图3 时间步长无关性验证
3.3 实验模型准确性验证
将本文模型模拟结果与文献[20]的模拟结果进行对比,以验证本文模型的准确性。如图4所示,在相同边界条件下,对水箱出口温度随着无量纲时间变化的分布进行比较,结果表明:本文模拟结果与文献[20]模拟结果最大误差为0.89%,考虑到所建立物理模型之间的差别,本文数值模拟结果与文献[20]模拟结果的误差在允许范围内,表明数学模型的准确性。
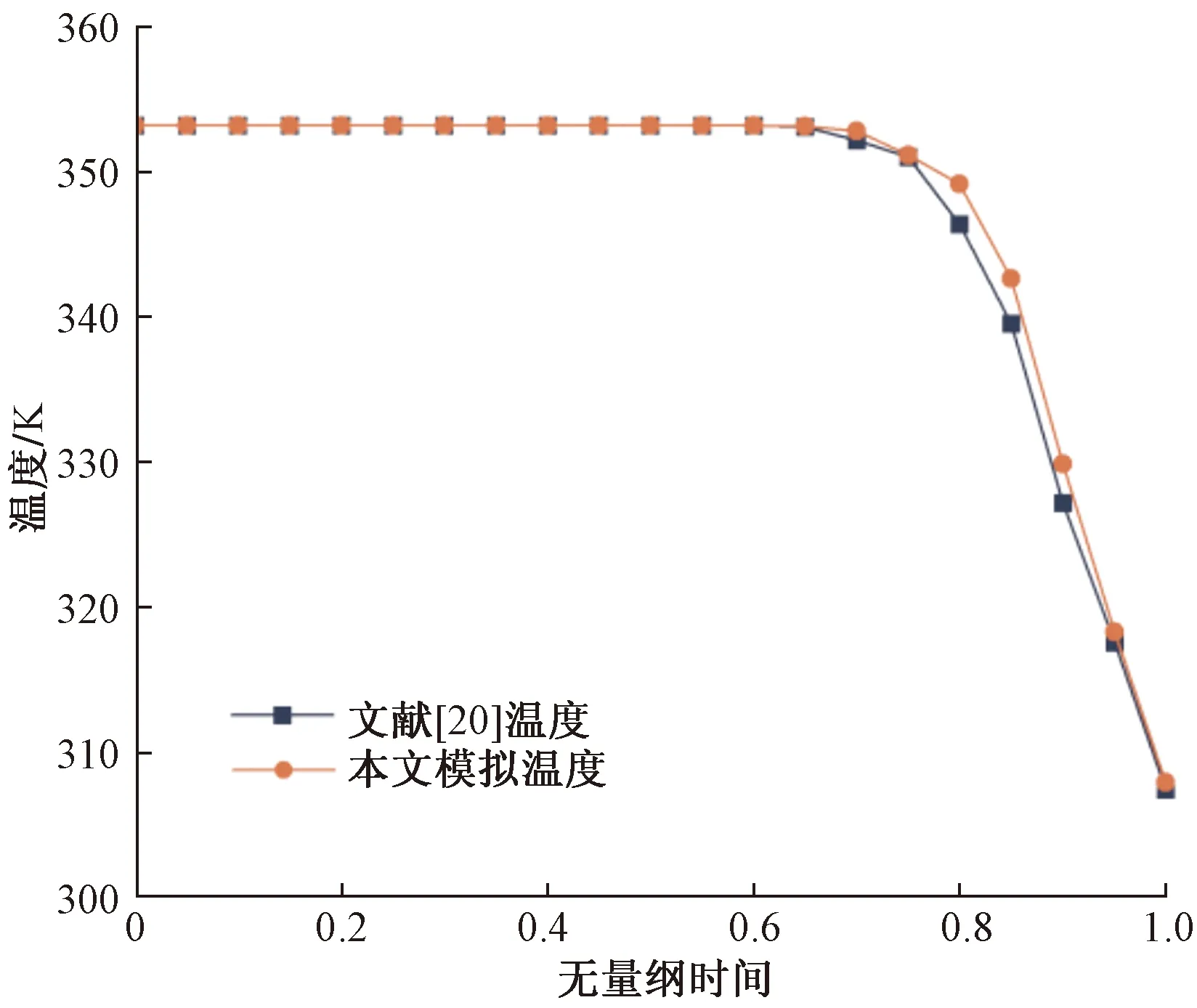
图4 模型准确性验证
3.4 相变蓄热胶囊液化率
进口流量4 L/min时,蓄热胶囊内部相变材料液化率变化如图5所示,蓄热胶囊分别在水箱高度为700、400、100 mm处。可以看出,在传热流体未与相变材料进行换热时,蓄热胶囊的液化率未发生变化,某一时刻后,蓄热胶囊的中心液化率发生了改变,由0开始上升,此时相变胶囊内的相变材料由固体变成液体,表明水箱内相变胶囊开始与流入水箱的热流体开始进行热交换并开始通过熔化的相变过程储存能量。在图中可以看出,距离水箱进水口处越近的相变胶囊其达到半衰期(液化率β=0.5)的时间就越短,即水箱内蓄热胶囊的半衰期随着水箱内相变胶囊位置的提高而缩短。距水箱底部700、400、100 mm处的相变材料开始相变的时间t*=0.2、0.4、0.65,而t*=1时,距水箱底部700、400、100 mm处的相变材料的液化率分别为0.77、0.73、0.36,结果表明:当相变胶囊距离入口越近时,其与流入水箱的热流体交换的热量就越多,相变的程度就越大,水箱内温度的热分层越明显。t*=1时,相变蓄热胶囊内相变材料液化率随相变胶囊距离水箱底部的高度增加而减小。
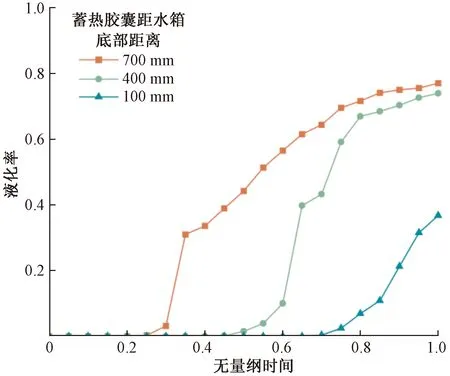
图5 相变蓄热胶囊液化率随位置变化
如图6所示,通过对3种尺寸半径分别为20、25、30 mm的蓄热胶囊测试,分析相变胶囊半径对于蓄热胶囊液化率的影响。进口流量为4 L/min时,3种尺寸的蓄热胶囊都在t*=0.4时开始相变,当相变胶囊尺寸为20 mm时,达到半衰期的时间为t*=0.7,中断时刻的液化率为0.73,随着相变胶囊半径增加到30 mm时,达到半衰期的时间延长至t*=0.8,中断时刻的液化率为0.55。结果表明:随着相变胶囊半径的增加,达到半衰期的时间增加,相变蓄热胶囊的熔化程度减小,所吸收的热量也随着减小,这主要是因为相变蓄热胶囊半径增加后,减缓了水箱内热流体的流动,降低了水箱内蓄热胶囊的液化率,使相变的过程进行的更加缓慢。
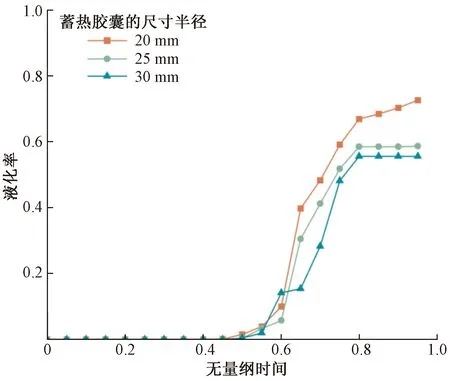
图6 相变蓄热胶囊液化率随尺寸变化
相变材料位于水箱高度为400 mm时,蓄热胶囊内相变材料液化率在相变传热过程中的变化如图7所示,当进口流量为2 L/min时,初始相变时间为t*=0.35,而当进口流量为8 L/min时,初始相变时间为t*=0.5。中断时刻时,进口为2 L/min液化率为0.88,进口流量为8 L/min时液化率为0.65。结果表明:相变胶囊中心液化率随着水箱入口流量的增长而降低,液化率达到50%所需的时间随着传热流体流速增加而增长,其原因主要是随着进口流量增加,虽然一定程度上加强了水箱内部的传热流动,但由于相变胶囊所能吸收热量的能力有限,且流动时间降低,水箱内热水置换循环较快,相变蓄热胶囊内部的相变材料还未来得及完全熔化就结束了换热过程。

图7 相变蓄热胶囊液化率随流量变化
3.5 相变蓄热胶囊理查德森数
储能水箱的利用效率受温度分层的影响,随着水箱内温度分层程度增加,储能水箱内的利用效率也会增加。理查德森数作为一种表征了浮升力与掺混力比值的无量纲数,其数值大小可以用来衡量水箱储能水箱内部的热分层情况,理查德森数越大,水箱内热分层程度就越高。
当水箱入口流量为4 L/min时,相变材料位于不同位置的Ri数在水箱内部换热过程的变化如图8所示。蓄热完成后,蓄热胶囊位于700 mm处的Ri数大于蓄热胶囊位于100 mm处的Ri数,表明当蓄热胶囊距离水箱底部的高度越高时,水箱内部的热分层效果越好。
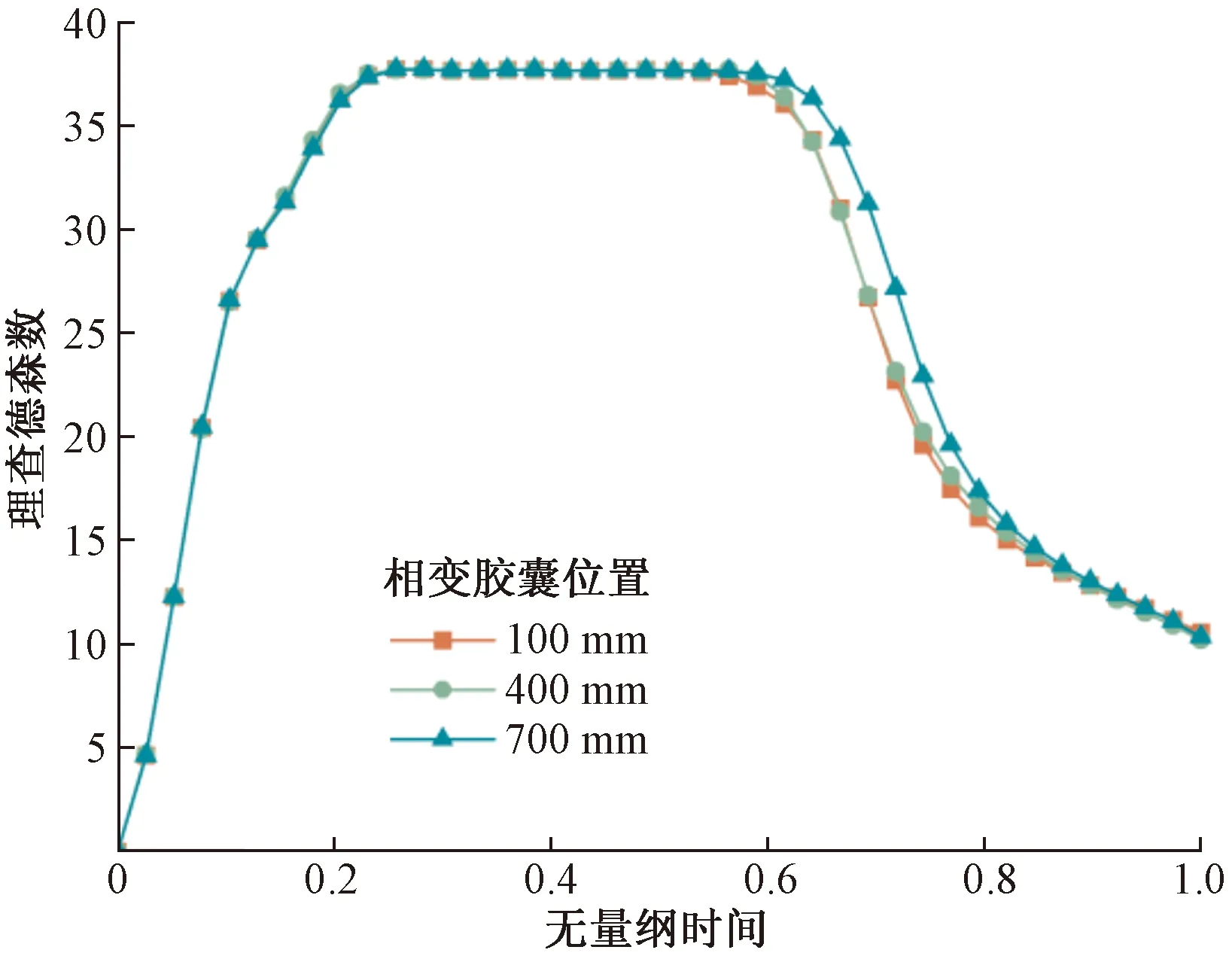
图8 理查德森数随相变胶囊位置的变化
图9为流量为4 L/min时,不同尺寸相变胶囊的Ri数在蓄热过程中的变化,可以看出,相变胶囊尺寸为20 mm时的Ri数大于相变胶囊尺寸为 30 mm 的Ri数,这说明了水箱热分层程度随着相变胶囊半径增加而减小。
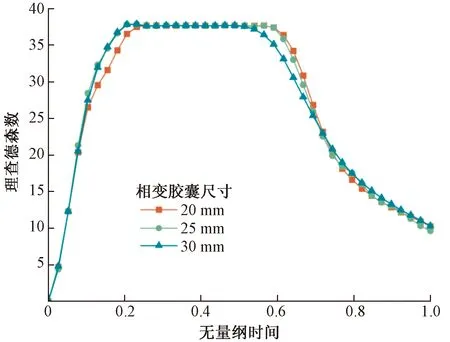
图9 理查德森数随相变胶囊尺寸变化
当蓄热胶囊位于高度为400 mm时,水箱不同入口流量的Ri在储热过程中的变化如图10所示,当流量为2 L/min时,水箱内Ri数为150,而当流量为8 L/min时,水箱内Ri数为9。这是因为随着流入水箱内部的传热流体速度越快,水箱内部的冷热流体混合变化也随之变快,随着热流体流入水箱越来越多,冷热流体之间的分层效果越来越模糊,Ri数越来越小,各层温度趋于一致,水箱内热分层程度也随之减小。通过Ri数的公式可以得知,影响Ri数的主要因素为水箱的入口流量与水箱顶部与底部的温差,因此水箱入口流量的变化水箱对Ri数变化的影响要比相变胶囊高度与相变胶囊尺寸对Ri数变化的影响要大,Ri数的变化也就更加明显。

图10 理查德森数随入口流量变化
3.6 平均蓄热率与蓄热密度
混合储能水箱的性能可以主要从传热特性与储热能力两个方面来进行评价。储能水箱的实际储能能力可以利用蓄热密度与平均蓄热率两个指标对其进行评价。
图11为当入口流量为4 L/min时,蓄热胶囊位于不同位置时对蓄热密度与平均蓄热率的影响。当相变胶囊处于高度为100 mm时,水箱内蓄热密度为39.04 kJ/m3,平均蓄热率为174.75 kJ/min,当相变胶囊的高度增加到700 mm时,水箱内蓄热密度为41.3 kJ/m3,平均蓄热率为184.91 kJ/min。蓄热密度增加了6%,平均蓄热率增加了5.8%。这是由于在储热能力和传热条件变化不大的条件下,相变胶囊高度的增加,增加相变胶囊与传热流体的接触时间,位于700 mm处的相变胶囊与流动热流体进行了更为充分的热交换,储存了更多的热量,由结果可知,水箱内平均蓄热密度与平均蓄热率随着相变胶囊高度的升高而升高。

图11 不同位置的蓄热密度与平均蓄热率
不同尺寸蓄热胶囊对于蓄热密度与平均蓄热率的影响如图12所示,当入口流量为4 L/min时,分别对相变胶囊半径为20、25、30 mm这3种尺寸进行了模拟测量,当相变胶囊半径从20 mm增加到30 mm时,蓄热密度由41.39 kJ/m3降低到 36.66 kJ/m3,降低了11.4%。蓄热率由184.90 kJ/min降低到164.13 kJ/min,降低了11.2%。主要原因是:由于蓄热胶囊直径增加,使得孔隙度增加,传热流体与PCM之间的传热面积减小,胶囊热阻增加,传热性能降低,所需蓄热时间增加。由于空隙的增大与传热面积的降低,使得水箱内的对流换热效果降低,因此水箱内蓄热密度与平均蓄热率随着相变胶囊半径的增大而减小。

图12 不同相变胶囊尺寸的蓄热密度与平均蓄热率
水箱入口流量分别为2、4、8 L/min时对水箱内蓄热密度与平均蓄热率的影响如图13所示。当水箱入口流量由2 L/min增加到8 L/min时,蓄热密度由19.05 kJ/m3增加到84.90 kJ/m3,平均蓄热率由85.27 kJ/min增加到380.05 kJ/min。结果表明:水箱内的蓄热密度与平均蓄热率随着水箱入口流量的增加而显著提升,这是因为在水箱内部结构与换热特性改变不大的情况下,入口流量的增加使水箱内对流换热的强度增加,对流热阻减小,有效蓄热所需时间减小,与此同时,由于入口流量增加所导致的较小的热力学损失,即摩擦力与流动引起的环境热力学损失对平均蓄热率与蓄热密度的影响远不及其总量的增加,因此可以得出结论:水箱内蓄热密度与平均蓄热率随着水箱入口流量的增加而增加。
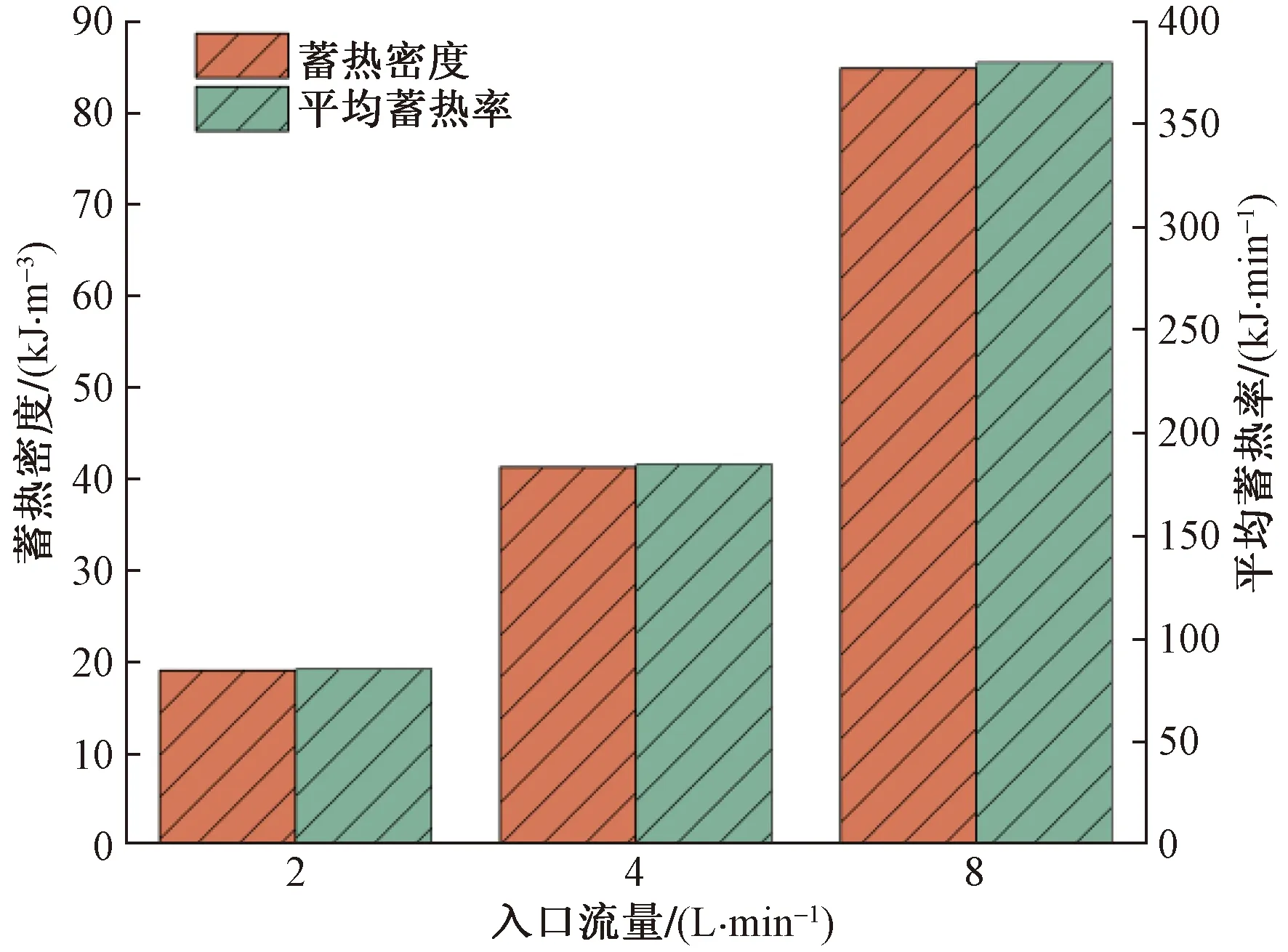
图13 不同入口流量的蓄热密度与平均蓄热率
4 结论
通过数值模拟研究了储能水箱内球形蓄热材料的熔化和凝固过程,建立了PCM区域的能量方程,数值模型包括:球形蓄热单元尺寸、球形蓄热单元位置以及水箱入口流速。得出以下结论。
(1)入口流量相同时,球形蓄热单元尺寸越小、越靠近水箱顶部时,储能水箱热分层效果越好。在尺寸相同、位置相同的情况下,相变胶囊入口流量越小,储能水箱的热分层效果越好。
(2)相变蓄热胶囊的液化率随着入口流量的增加而降低,在位置相同与相变蓄热胶囊尺寸相同的情况下,入口流量为2 L/min时,中断时刻的相变蓄热胶囊的液化率为0.88。当入口流量为8 L/min时,中断时刻相变蓄热胶囊的液化率为0.65。
(3)入口流量相同时,蓄热密度与平均蓄热率随着相变蓄热胶囊位置的升高而增加,随着相变蓄热胶囊尺寸的减小而增加。在相变蓄热胶囊位置与尺寸相同的条件下,蓄热密度与平均蓄热率随着入口流量的增加而增加。
