基于2-PCR_2-UPS并联机构的运动学分析与工作空间
2023-03-15贺阳涛马春生文杰刘建国李瑞琴
贺阳涛,马春生,文杰,刘建国,李瑞琴
(中北大学机械工程学院,太原 030051)
相比于串联机构,并联机构具有刚度高、精度好、承载能力强和动态响应快等优势[1-2]。在一些精度要求较高的场合,串联机构因某些精度限制不能满足要求,并联机构则可以广泛应用到各种场合。
近年来,并联机构相关领域的理论研究取得相当程度的发展,并且在生活生产中的应用也越来越广泛。张俊辕等[3]通过对2-RPU/UPR并联机构的相关分析验证了其在应用方面的合理性。李特奇等[4]应用Adams软件分析验证了2RRS/2UPS机构的驱动选取的合理性问题。胡健等[5]提出了一种2-RPU/UPS并联机构并对其展开了运动学分析。史宝周等[6]结合Adams与MATLAB软件对3-UPS机构关节约束反力的计算方法进行了分析验证。袁成志等[7]利用MATLAB编程计算分析对码垛机器人进行了连杆参数优化。董海涛等[8]通过SolidWorks和MATLAB以及Simulink对建立的码垛机器人进行了动力学仿真分析。但上述研究多是基于理论研究,缺少工程实践运用。
为此,提出一种2-PCR_2-UPS非对称并联机构,同时可运用于其他行业产品的码垛与分拣。利用SolidWorks软件中对2-PCR_2-UPS并联机构进行建模;根据螺旋理论对2-PCR_2-UPS机构的自由度进行分析,并结合修正的G-K(Grübler-Kutzbach)公式验证其正确性;在求解机构的运动学逆解过程中主要运用闭环矢量法,使用MATLAB程序语言绘制得出机构工作空间;在Adams软件中建立虚拟样机进行仿真分析以证实机构设计的可行性,为下一步的实践提供了理论基础。
1 2-PCR_2-UPS机构构型及自由度分析
如图1所示,2-PCR_2-UPS并联机构由2条PCR支链、2条UPS支链、静平台以及动平台组成。相同的运动支链呈现相对分布,PCR支链的移动副(P)沿X轴方向排布,圆柱副(C)可以同时实现Z轴方向上的移动和转动,以及绕Z轴转动的转动副(R)。UPS支链的虎克铰(U)可同时完成X与Y方向的转动,球副(S)位于动平台上,二者中间通过移动副相连。
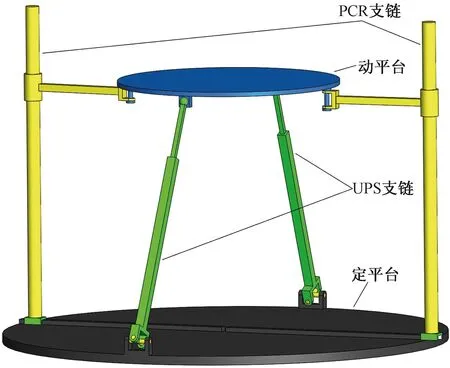
图1 2-PCR_2-UPS并联机构
如图2所示,定平台在下方、动平台在上方,并且二者的外形轮廓都是圆形,A1A3与A2A4互相垂直、B1B3与B2B4互相垂直,C2B2杆和C1B4杆两杆杆长相等且与动平台水平。定平台圆心O到A1、A2、A3、A4点的距离都是R,动平台圆心O0到B1、B2、B3、B4点的距离都是r。固定坐标系O-XYZ和动坐标系O0-X0Y0Z0如图2所示。
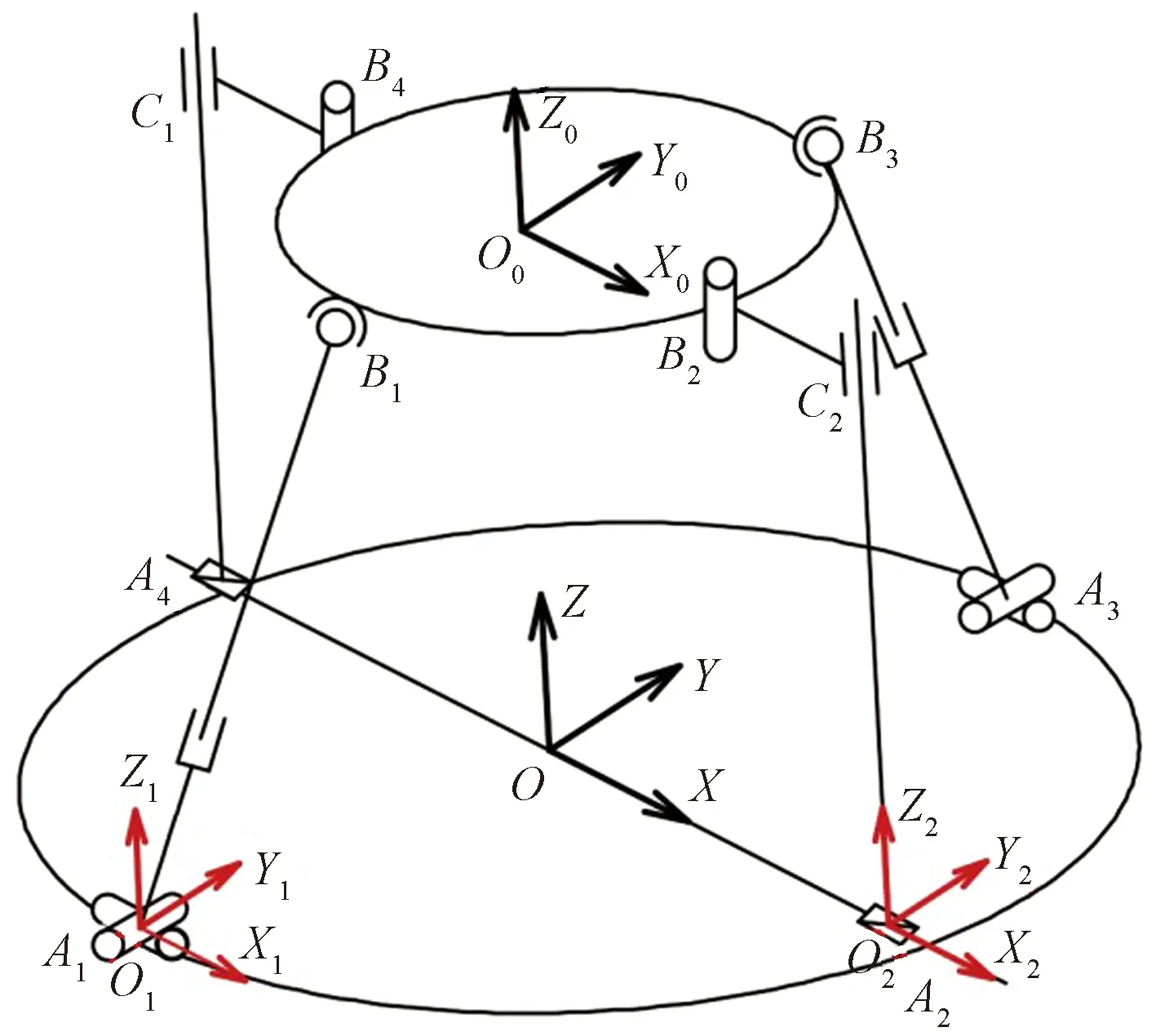
图2 2-PCR_2-UPS机构简图
依据螺旋理论[9-10],求解得出机构自由度。
首先对UPS支链展开分析,并以虎克铰U副的中心为原点建立图2所示的局部坐标系A1-X1Y1Z1,得到运动螺旋系为
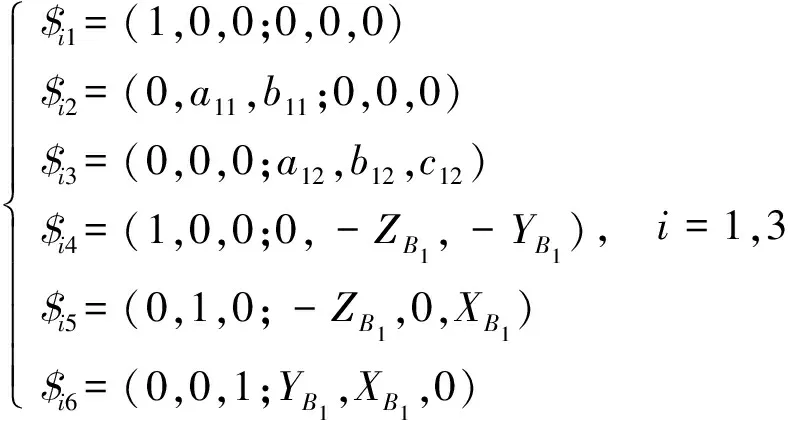
(1)
式(1)中:$i1~$i6为UPS支链的运动螺旋;a11、b11为U副中一个转轴轴线坐标分量;(a12,b12,c12)为P副的方向余弦;(XB1,YB1,ZB1)为B1点坐标。
由式(1)可知,上述所求的6个运动螺旋互相之间是线性无关的,即对动平台无任何的约束。
对支链PCR而言,以移动副的移动中心为原点建立局部坐标系A2-X2Y2Z2,如图2所示。求得运动螺旋系为
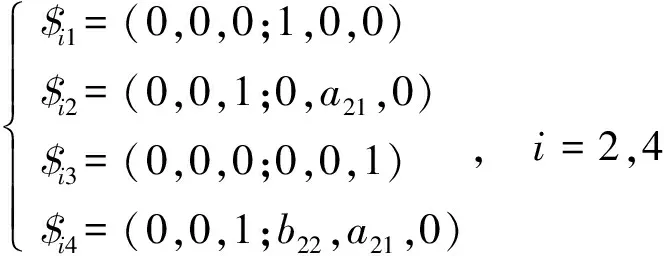
(2)
式(2)中:a21为A2点在X方向上的分量;b22为B2点在Y方向上的分量。
对式(2)求反螺旋,求得其约束螺旋系为
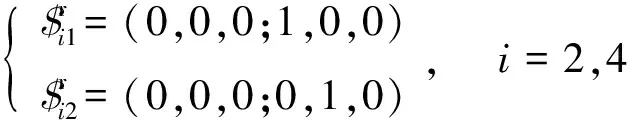
(3)
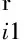
通过上述的分析,对式(3)进行反螺旋的求解,继而可知机构的运动螺旋系为

(4)
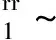
综上所述,2-PCR_2-UPS并联机构拥有的自由度数目是4,分别为沿X、Y、Z三轴的移动以及绕Z轴的转动。修正的G-K公式为
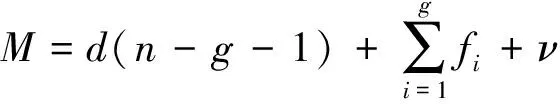
(5)
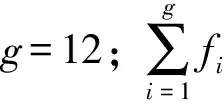
求得M=4,即机构有4个自由度,与螺旋理论所求结果一致。
2 2-PCR_2-UPS机构位置逆解分析
采用封闭矢量法[12]对2-PCR_2-UPS机构的每个支链进行逆解分析。
2.1 对UPS支链进行运动学逆解
对于UPS支链进行运动学逆解分析,在计算过程中,已知动平台O0在定坐标系O-XYZ下的空间坐标为O0=(x,y,z)、姿态角为(α,β,γ),即动坐标系分别绕定坐标系x、y、z轴转动的角度,li(i=1,3)为UPS支链中P副的长度量,即AiBi(i=1,3)的长度量。
在O-XYZ下A1点的坐标为
A1=(0,-R,0)
(6)
在O0-X0Y0Z0下B1点的坐标为
B1=(0,-r,0)
(7)
动平台的旋转矩阵为
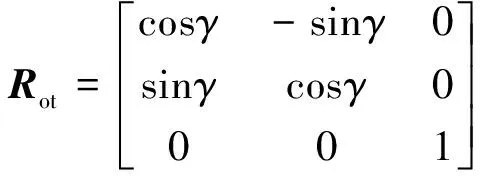
(8)
点B1在定系下的表达式为
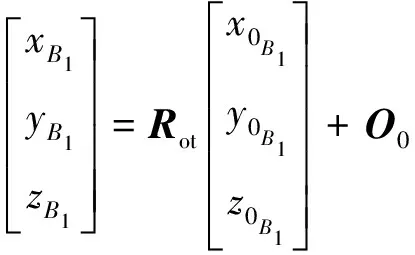
(9)
求得B1的绝对坐标为
B1=(x+rsinγ,y-rcosγ,z)
(10)
运用几何关系,可得
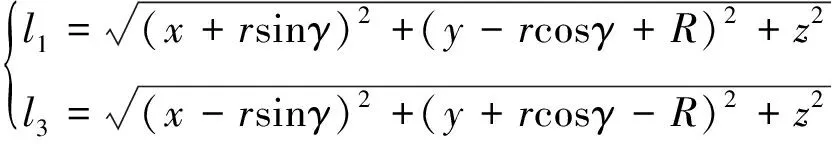
(11)
2.2 对PCR支链进行运动学逆解
对于PCR支链,设C1B4杆和B2C2杆的杆长皆为l5,li(i=2,4)为PCR支链中P副的长度量,即OAi(i=2,4)的长度,在求解过程中,(x,y,z,α,β,γ)均为已知参数。
在O-XYZ下C2点的坐标为
C2=(l2,0,z)
(12)
在O0-X0Y0Z0下B2点的坐标为
B2=(r,0,0)
(13)
动平台的旋转矩阵如式(8)所示。点B1在定系下的表达式如式(9)所示。
求得B2的绝对坐标为
B2=(x+rcosγ,y+rsinγ,z)
(14)
利用几何关系,可求得
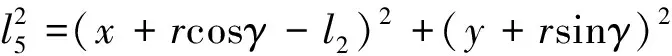
(15)
求得
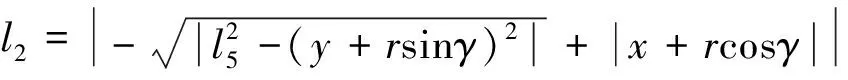
(16)
同理可得
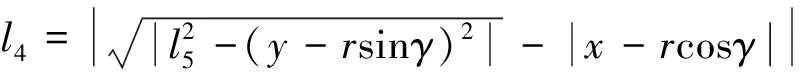
(17)
3 工作空间
通过工作空间分析便于更直观地了解机构的运动空间范围,工作空间的主要影响因素包括:移动副的活动范围、运动副的转角范围和机构奇异位型[13-15]。所设计的机构主要固定值为:定平台直径为400 mm,动平台直径为200 mm,l5的杆件长度是150 mm。限制的约束分为移动副的移动量约束和一定数量的转动约束,包括:移动杆l1和l3的最小值为70 mm、最大伸长量是500 mm,移动副A2与A4的位置(即杆l2与杆l4的长度)最小值距离到定平台圆心距离为5 mm、最大距离到定平台圆心距离为 300 mm;U副的X轴方向的转动限制为0°~90°、Y轴方向的转动限制为-90°~90°以及C副绕Z轴转动的限制为-90°到90°。然后通过MATLAB编程,同时限制移动副与转动轴的活动范围,求出机构的运动学逆解,进而得出机构所有的可达点位置并记录下来,最后利用函数关系绘制工作空间[16-17],最终的工作空间如图3所示。通过观察分析,2-PCR_2-UPS机构没有奇异位置,在X-Y平面内动平台绕Z轴转动的角度最大为90°,具有较大范围的工作空间。
4 2-PCR_2-UPS机构仿真分析
为机构的运行平稳,防止因突然抖动而导致运输产品的破坏,采用Adams软件对机构的逆向运动学过程进行仿真分析,对机构的实际运动性能进行科学的预测分析。.
在Adams中导入2-PCR_2-UPS并联机构的模型,对其中的各构件进行相应的运动副连接,建立图4所示的虚拟样机模型。在进行仿真分析之前,再次验证机构自由度的准确性。然后在动平台中心点施加式(18)所示的驱动函数,仿真时间10 s,步数2 000步,结果如图5~图7所示。
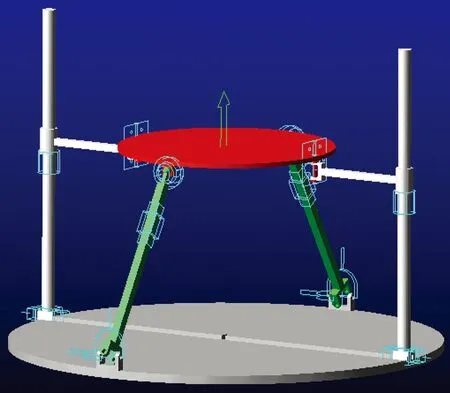
图4 虚拟样机模型
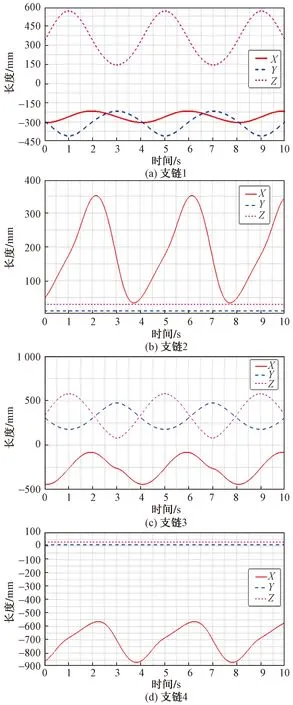
图5 各支链移动副的长度沿坐标轴分量变化曲线
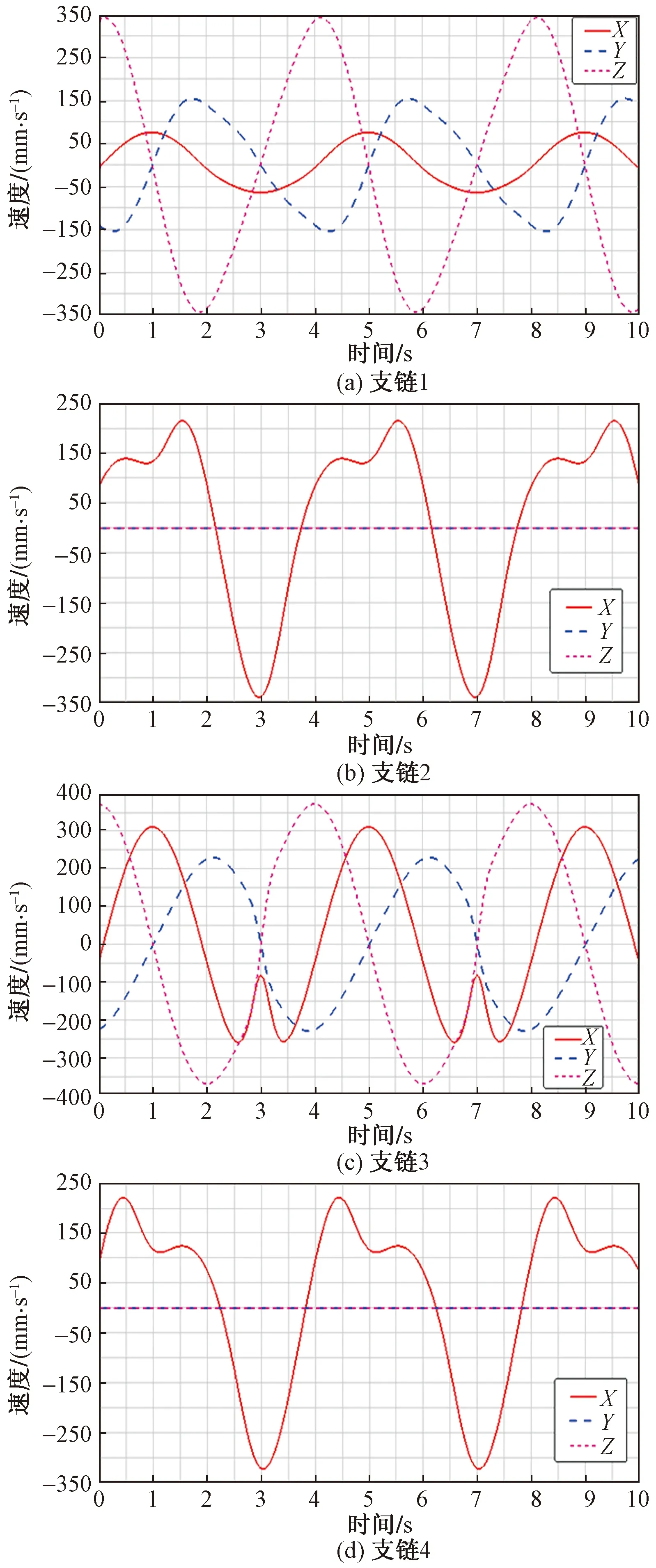
图6 各支链移动副的速度沿坐标系分量变化曲线
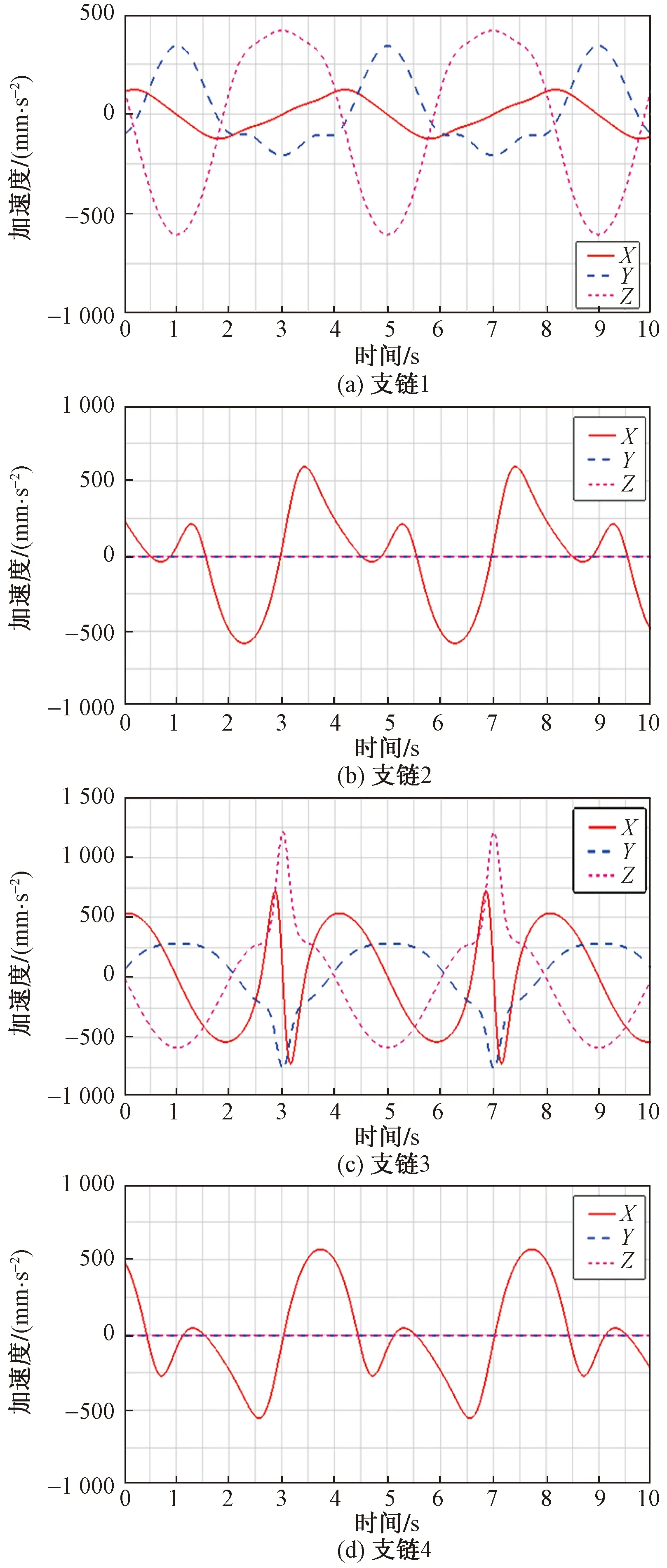
图7 各支链移动副的加速度沿坐标系分量变化曲线
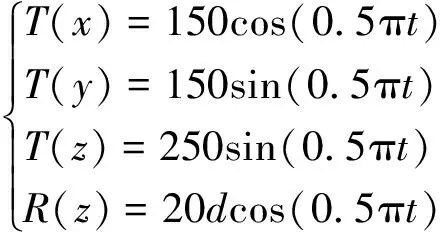
(18)
式(18)中:T为施加的移动方向驱动函数;R为施加的转角驱动函数;t为仿真时间。
从图5(a)和图5(b)可以看出,UPS支链中P副的移动规律呈现周期性变化,运动平稳,便于进行驱动控制。并且两个子图中的Z轴方向的长度分量是完全同步的,进一步证明了动平台在运动过程中的平稳性。从图5(c)、图5(d)可以看出,PCR支链中P副只能实现X方向的移动,对机构的构型分析进行了验证。
结合速度和加速度变化曲线,发现约3 s时各支链的波动幅度较大,尤其是支链3在X轴方向的加速度变化。并且通过相同时间段(图5)的位移曲线可以看出,此时动平台距离定平台较近。这就要求在实际的控制过程中,当动平台距离静平台较近时,需要降低各杆件移动副的运动速度,以保证机构运动的平稳性。
从图5~图7曲线的变化规律可以看出,各个驱动副在运动过程中无间断点和突然的跳动,运动过程平稳且连续,所以该并联机构完全可以适用于码垛、分拣的工作。
5 2-PCR_2-UPS机构的工程应用分析
2-PCR_2-UPS机构可以通过绕Z轴的旋转改变快递件的摆放角度,以达到规整产品的目的;同时可以通过X、Y、Z3个方向上的移动完成对不同高度快递件的要求将其摆放到相应位置。
在实际生活中,快递件的平均尺寸为290 mm×150 mm×190 mm,2-PCR_2-UPS机构的动平台是直径200 mm的圆,可以实现快递件的抓取工作;并且快递件重量不超过10 kg,2-PCR_2-UPS机构可以完成相应快递件的分拣工作;在快递分拣车间,传输带的宽度尺寸平均为400 mm,2-PCR_2-UPS机构的工作空间完全可以实现相邻或相接传输带间快递的分拣工作。
2-PCR_2-UPS机构对快递产品的分拣工程实例,如图8所示。在SolidWorks中完成对支架、吸盘的三维建模之后,在快递分拣流水线上对该并联机构进行仿真分析,位于动平台上的吸盘将目标快递件从一条传送带上取走[图8(a)];最后将快递产品运送到另外一条目标传送带上[图8(c)],完成整个分拣工作。整个运动过程平稳有序,在快递行业的流水线上具有很好的应用前景。
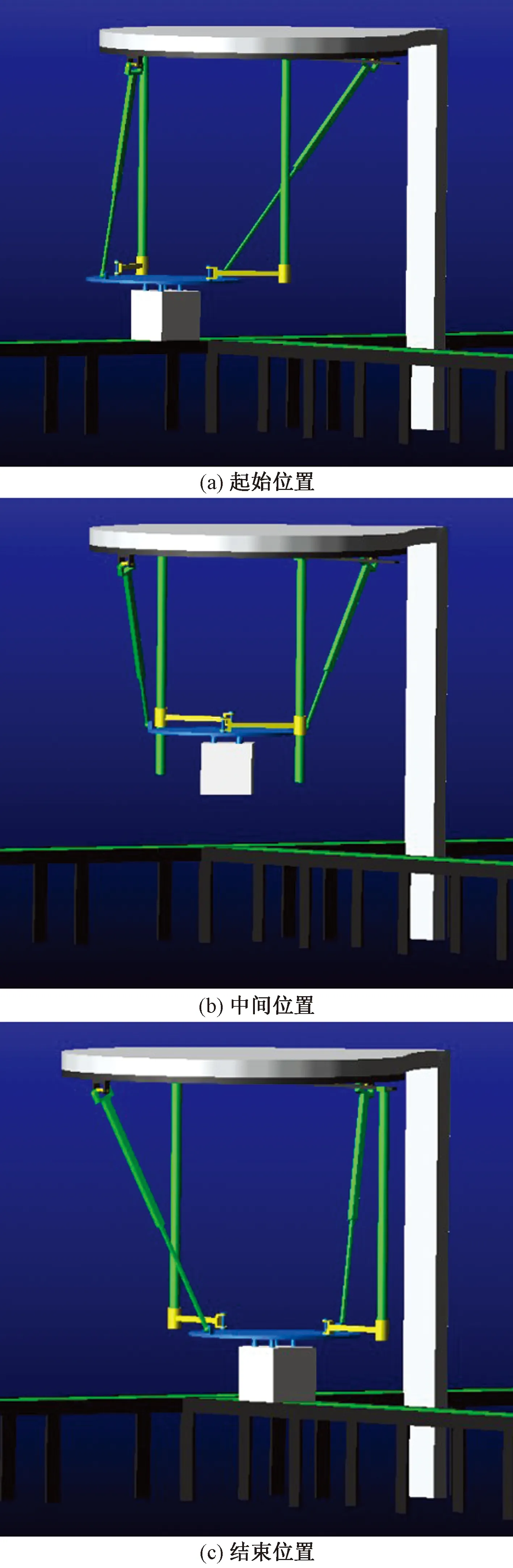
图8 2-PCR_2-UPS并联机构的分拣工程应用
6 结论
(1)通过2-PCR_2-UPS并联机构的建模以及螺旋理论的分析,得出机构自由度为4,即沿X、Y、Z轴方向上的移动与围绕Z轴的转动,结合修正的G-K公式验证其准确性。在求解运动学逆解过程中主要使用闭环矢量法,为机构的驱动副选取提供了基础。
(2)通过在MATLAB中绘制出机构的工作空间,经过观察得出,机构工作空间范围广、整体呈对称分布、空间性能良好,通过Adams仿真分析可以得出机构运动过程连续且平稳,可以满足各类快递件的码垛与分拣工作,同时在其他行业的码垛与分拣工作中也具有广泛的适用性。
