深层碳酸盐岩地层长水平段钻井井筒温度分布模型研究
2023-03-15欧彪董波严焱诚江波肖东
欧彪,董波,严焱诚,江波,肖东
(1.中石化西南油气分公司石油工程技术研究院,德阳 618000;2.中石化西南油气分公司彭州项目部,成都 610000;3.西南石油大学油气藏地质及开发工程国家重点实验室,成都 610500)
深层碳酸盐岩油气资源在四川盆地天然气生产中占有极为重要的地位,其层系资源量占四川盆地常规天然气资源量的85%,已经成为川西常规天然气增储上产的重要领域[1-3]。彭州地区位于川西平原腹地,人口密集,农田肥沃,旅游资源丰富,井位部署和井场选址受到一定限制。为了节约井场用地,保护环境,便于集中管理及后期施工,降低开发成本,“井工厂”丛式井是目前川西彭州地区钻探雷口坡海相气藏的施工模式。然而,深层碳酸盐岩储层的超深(垂深5 500~8 000 m),使得钻遇高温高压地层异常普遍;丛式井各分支井水平段超长,井眼轨迹控制难度大等问题给钻井工程带来了巨大的挑战[4]。旋转导向工具为其三开钻进的井眼轨迹控制提供了重要的技术支持,但由于井底循环温度高,旋转导向工具和近钻头仪器因耐温性差而频繁发生故障,钻井时效极低。据现有钻井资料统计,彭州7#、6#、4#平台在钻井过程使用旋转导向工具19趟次,故障16趟次,故障率高达84.21%。此外,过高的地层温度还造成了钻具腐蚀,钻井液失效及井壁失稳[5-6]等不利影响。Suryadi等[7]认为预测钻井工具在井下工作的环境温度是高温井钻井作业成功的关键因素[7]。因此,有必要对水平井井筒循环温度分布规律开展研究,以保障钻井施工顺利进行。
近10年来,因温度井筒压力控制、井壁稳定性预测、井下动力钻具与测量设备优选带来一系列的技术挑战,实时认清钻井过程中井下温度分布规律研究得到了进一步的发展。李梦博等[8]建立了非牛顿流体螺旋流动的钻井井筒温度分布模型,指出钻柱旋转对井底温度的影响很大。王宁等[9]以注入和返出温度为边界条件,推导得到了井筒温度场的解析解,可应用于变钻具尺寸、变井身结构及变温度梯度的温度分布。王江帅等[10]充分考虑钻井过程中岩屑进入环空后对流体热学性能的影响,建立了循环钻进过程中井筒温度场的计算新模型。Li等[11]建立了水平井钻井综合循环温度模型,发现水平段长度、旋转钻井中机械能和钻井液水力能的传热是水平井井底温度高于静态地层温度的主要原因。付建红等[12]建立了深层页岩气水平井井筒瞬态温度场模型,并提出了降低井筒循环温度的具体措施。Wang等[13]建立了井筒传热模型,用以预测井筒在井漏条件下的温度分布,模型充分考虑了井漏、复杂套管程序和热源等因素对井漏条件下井筒温度的影响,提高了模拟结果的准确性。王磊等[14]考虑钻柱与井壁、套管直接的摩擦生热效应建立了海域天然气水合物水平井钻井过程的井筒温度剖面计算模型。
上述研究为准确预测井筒温度奠定了基础。然而,针对海相碳酸盐岩气藏水平段钻进特征,以上模型还存在一些不足,主要表现在以下三个方面:①所采用的白油基钻井液物性受温度及压力影响更大;②水平段钻进过程中钻柱的偏心,增加了钻柱与井壁间的摩阻生热源项;③碳酸盐岩地层的破碎性,增加了释热源项。因此,现针对海相碳酸盐岩储层水平段钻井过程特征,综合考虑白油基钻井液物性参数随温度变化、钻柱与井壁摩擦及非牛顿流体螺旋流动的传热机理,建立一种新的井筒传热模型,以此预测深层碳酸盐岩地层长水平段钻进过程的井筒温度分布,进而为克服深层碳酸盐岩地层长水平段钻井的高温问题提供必要的理论基础。
1 井筒传热模型
1.1 水平井钻井过程物理模型
深层海相碳酸盐岩水平井的结构和钻井液循环如图1所示。白油基钻井液从钻杆注入并从钻头喷嘴喷出,从环空携带岩屑返至地面完成循环。整个传热过程可描述如下。
(1)钻杆内的钻井液与从环空返回的钻井液进行热交换。同时,钻杆内由于钻井液流动摩阻等原因产生了一部分热量。
(2)从环空返回的钻井液与钻杆内的钻井液进行热交换的同时从地层中吸收热量。此外,由于钻井液在环空中的流动摩阻、钻柱旋转、环空中钻杆与井筒之间的接触摩擦、岩石破碎等原因,会产生另一部分热量。
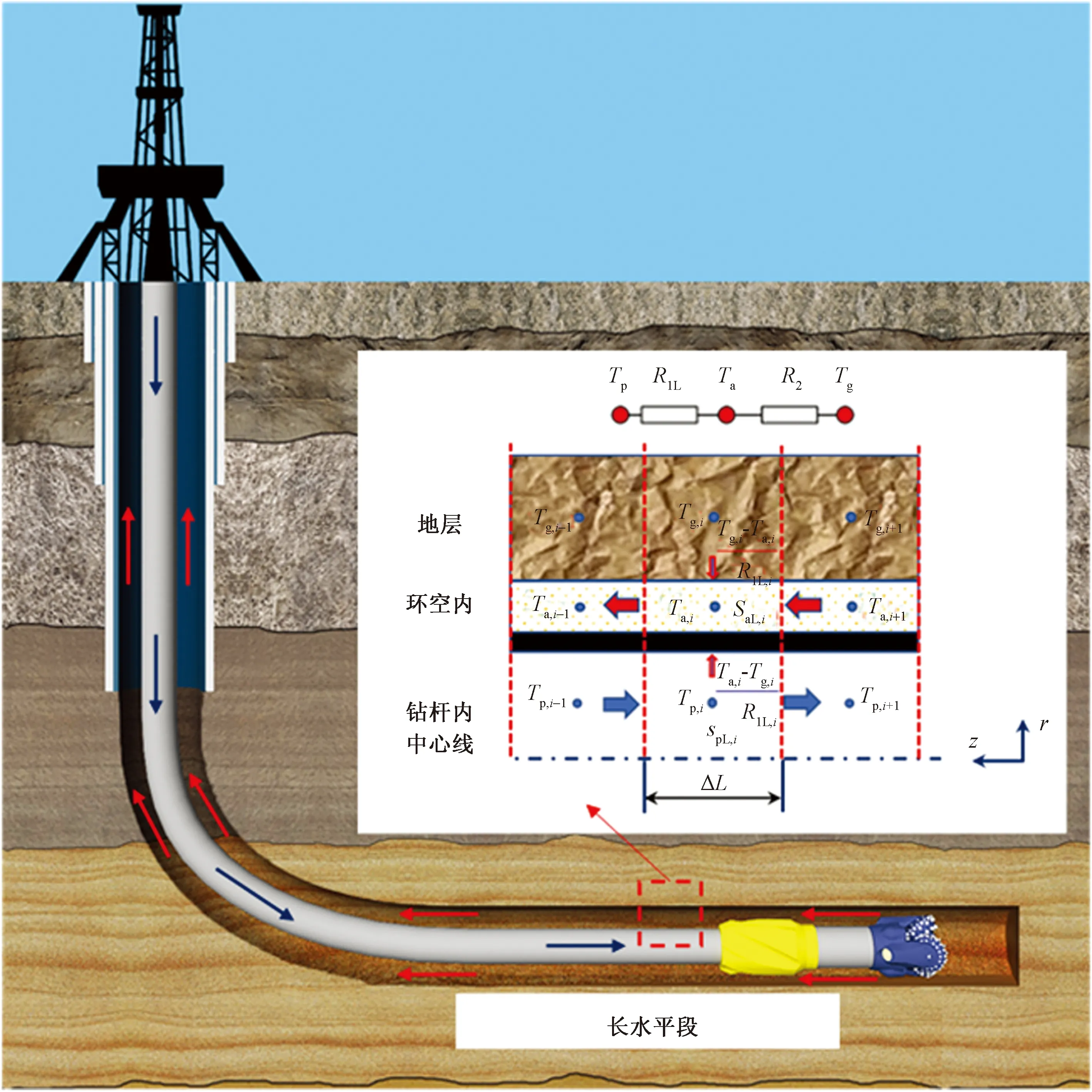
Tp、Ta分别为钻杆内和环空内的流体温度,℃;Tg为地层温度,℃;R1L为钻杆导热热阻、钻杆内外壁面与钻井液的对流换热热阻之和,(K·m)/℃;R2L为环空内钻井液与井壁的对流换热热阻、套管与水泥环的导热热阻(固井段有,裸眼段无)、地层热阻之和,(K·m)/℃;SaL为单位长度环空内由于各种原因产生的热量,W/m;SpL为单位长度钻杆内的生热量,W/m图1 水平井水钻井过程中井筒模型图Fig.1 Schematic of the horizontal well and heat transfer process
1.2 水平井钻井过程中传热数学模型
1.2.1 控制方程
1)钻柱内控制方程
(1)钻柱内钻井液温度分布模型为
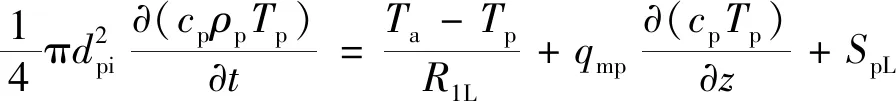
(1)
式(1)中:cp为钻杆内微元体中钻井液的热容,J/(kg·℃);ρp为钻杆内微元体中钻井液的密度,kg/m3;qmp为钻杆内中钻井液的质量流量,kg/s;dpi为钻杆内径,m。
(2)钻柱内钻井液压力分布模型为

(2)
式(2)中:pp为钻杆内钻井液的压力,Pa;vp为钻杆中钻井液流速,m/s;g为重力加速度,9.81 m/s2;θ为井斜角,(°);fp为钻杆内循环摩擦系数。
2)环空内控制方程
(1)环空内钻井液温度分布模型为
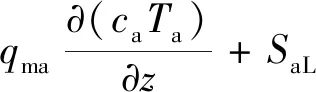
(3)
式(3)中:ca为环空内钻井液的热容,J/(kg·℃);ρa为环空内钻井液的密度,kg/m3;qma为环空内钻井液的质量流量,kg/s;dai、dpo为套管内径和钻杆外径,m。
(2)环空内钻井液压力分布模型为
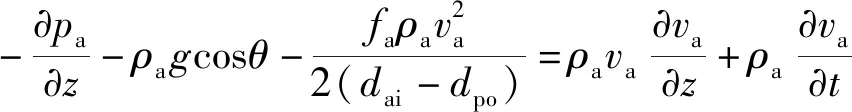
(4)
式(4)中:pa为环空内钻井液的压力,Pa;va为环空中钻井液流速,m/s;fa为环空内循环摩擦系数。
1.2.2 辅助方程
为了进一步使得方程封闭,需要引入相关的辅助方程。
1)热物性参数
在钻井过程中,随着井筒温度的变化,钻井液的热物性也随之变化。为了提高温度模型的准确性,本模型将钻井液的密度、导热系数、比热容和黏度随温压变化纳入考虑。
(1)密度。白油基钻井液的密度利用Furbish等[15]推荐的方程形式进行拟合
ρp=ρ0[1-βT(T-T0)+βp(p-p0)]
(5)
式(5)中:ρ0为参考温度压力下钻井液的密度,kg/m3;T0为参考温度,℃;p0为参考压力,Pa;βp、βT为经验常数,根据实验数据拟合后,取βp=4.094 4×10-10,βT=4.558 28×10-4。
(2)黏度。白油基钻井液的表观黏度利用Hermoso等[16]推荐的方程形式进行拟合,该方程为
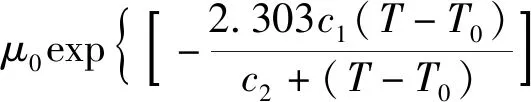
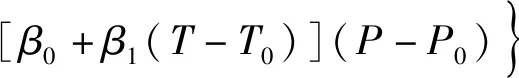
(6)
式(6)中:μ0为参考温度和压力下的表观黏度,Pa·s;c1、c2、β0、β1为经验常数,根据实验数据拟合后,取μ0=0.060 Pa·s,c1=1.58,c2=138.7 ℃,β0=2.04×10-8Pa-1,β1=-2.1×10-10Pa-1·℃-1。
(3)导热系数与比热。文献[17]中给出了经验公式用于描述水的导热系数及比热与温度的关系,也可将其推广至钻井液类似性质的表述中,即
λp=a1+a2T+a3T1.5+a4T2+a5T0.5
(7)
cp=b1+b2T+b3T1.5+b4T2+b5T0.5
(8)
式中:λp为钻井液导热系数,W/(m·℃);cp为钻井液比热,J/(kg·℃);a1、a2、a3、a4、a5、b1、b2、b3、b4、b5为经验常数,根据实验数据拟合后确定,利用彭州区块所用钻井液测试后,可得a1=0.845 567,a2=0.015 49,a3=-0.001 54,a4=5.66×10-5,a5=-0.064 84,b1=1 583.133,b2=-7.203 63,b3=2.939 88,b4=-0.363 3,b5=0.014 559。
考虑钻井过程中岩屑的影响,混入岩屑的钻井液密度为
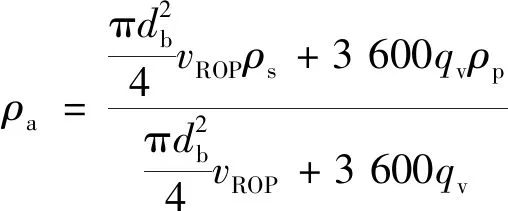
(9)
式(9)中:db为钻头直径,m;vROP为机械转钻速,m/h;ρs为岩屑密度,kg/m3;qv为循环排量,m3/s;ρp为钻井液密度,kg/m3。
岩屑的混入也影响到了环空钻井液的导热系数和比热容,可采用质量分数加权平均法计算钻屑侵入后的混合导热系数和比热容,即
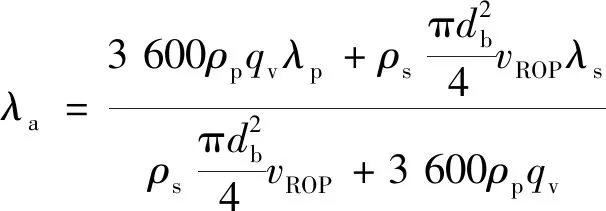
(10)
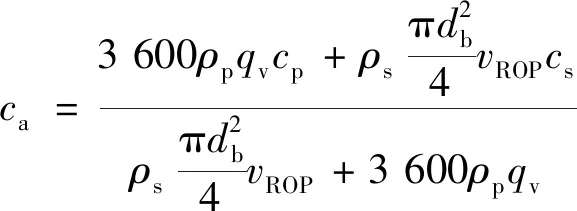
(11)
式中:λs为岩屑的导热系数,W/(m·℃);cs为岩屑的比热,J/(kg·℃)。
2)传热热阻
根据热电比拟思想,式(1)与式(3)中的热阻R1L和R2L分别为
R1L=RhL1+RλLp+RhL2
(12)
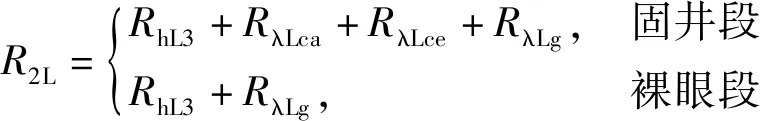
(13)
式中:RhL1为单位长度钻杆内壁与钻杆内钻井液之间的对流换热热阻,℃·m/W;RλLp为单位长度钻杆的导热热阻,℃·m/W;RhL2为单位长度钻杆外壁与环空钻井液之间的对流换热热阻,℃·m/W;RhL3为单位长度套管或裸眼井壁与环空钻井液之间的对流换热热阻,℃·m/W;RλLca为单位长度套管的导热热阻,℃·m/W;RλLce为单位长度水泥环的导热热阻,℃·m/W;RλLg为单位长度的地层热阻,℃·m/W。
其中对流换热热阻(包括RhL1、RhL2、RhL3)为
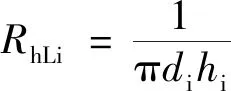
(14)
式(14)中:hi为对流热系数,W/(m2·℃),是确定对流换热热阻的关键。可用努塞尔数的定义式反解,即
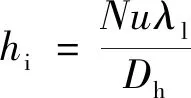
(15)
式(15)中:Nu为努塞尔数;Dh为管道的水力直径,m;λl为流体的导热系数,W/(m·℃)。
对于钻杆中的强迫对流,当流体在绕其轴线旋转的管道中流动时,旋转对传热的影响在层流和湍流状态下可以忽略不计。因此,可认为钻杆中的传热与静止管中的传热没有差别。对于环空中的强迫对流,由钻柱旋转产生的螺旋流动使其计算更加复杂,利用Fenot等[18]提出的等效雷诺数来校正环空流体的传热系数
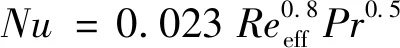
(16)
式(16)中:Pr为普朗特数;Reeff为等效雷诺数,其定义公式为
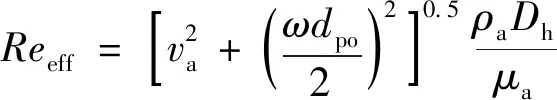
(17)
式(17)中:μa为环空钻井液表观黏度,Pa·s;ω为钻杆旋转的角速度,rad/s;dpo为钻杆外径,m。
导热热阻(包括RλLp、RλLca、RλLce)为
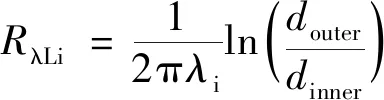
(18)
式(18)中:λi为该层材料的热导率,W/(m·℃);dinner和douter分别为该层材料的内径和外径,m。
地层热阻(Rλg)[19]为
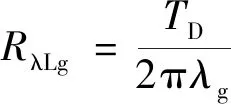
(19)
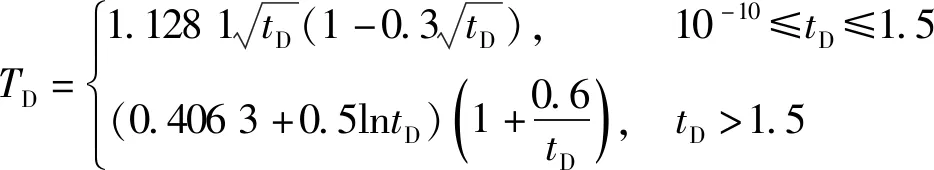
(20)
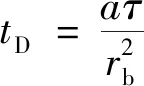
(21)
式中:TD表示无量纲温度;tD是无量纲时间;λg为地层的热导率,W/(m·℃);a为地层的热扩散系数,m2/s;τ为钻井液与地层的累积接触时间,s;rb为井筒结构与地层界面的同心圆半径,m。
3)热源项的计算
根据钻井过程中的能量传递过程,式(1)与式(3)中的热源项SpL和SaL,包括流动摩阻生热、钻头节流压降生热、钻头破碎岩石生热及钻杆与井壁的机械摩擦生热等。
(1)流动摩阻生热源项。钻井液在流道内流动过程中,因其黏性导致部分机械能损失,最终转化为热能,根据流体力学基本原理,钻杆内的摩阻生热源项为
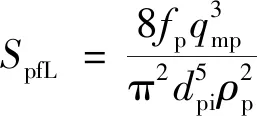
(22)
环空内的摩阻生热源项为
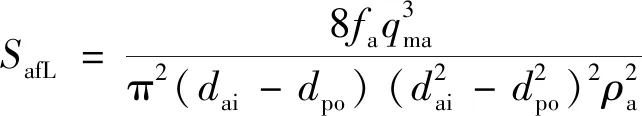
(23)
(2)钻头节流压降生热源项。钻井液通过钻头喷嘴产生较大的节流压降,这部分节流压降也将转化为热能,成为钻头节流压降生热源项,可用Xiao模型[20]计算,即
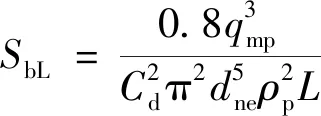
(24)
(3)机械摩擦生热源项。钻柱在钻井过程中,钻杆发生偏心并与井壁产生机械摩擦,机械摩擦转化为热能是环空钻井液的热源之一。在彭州海相碳酸盐岩水平段的钻进过程中,通常采用旋转钻进和滑动这两种钻进方式。两种钻进方式的技术原理具有明显区别,其产生的摩擦热源项计算也不同。
针对旋转钻进时钻杆与井壁之间的机械摩擦生热可用Kumar公式[21]计算,即
SamL=Tpipeω
(25)
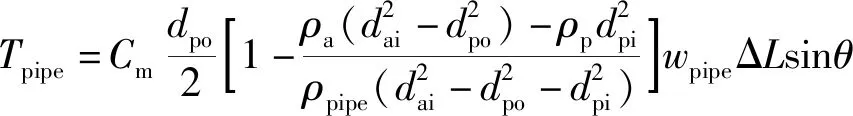
(26)
式中:SamL为机械摩擦生热源项,W/m;Tpipe为钻杆扭矩,kN/m;Cm为机械摩擦系数,根据彭州4-4D井井深7 113 m附近起下钻实际反演,并附加一定安全系数可得套管内为0.26,裸眼内为0.4;wpipe为空气中单位长度钻杆重量,kN/m;ΔL为钻杆长度,m。
针对滑动钻进,当不考虑钻杆屈曲变形等因素,滑动钻井的摩擦生热源项为
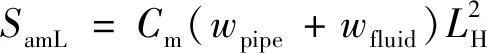
(27)
式(27)中:wfluid为单位长度井眼内钻井液的重量,kN/m;LH为水平段长度,m。
(4)钻头破碎地层生热源项。碳酸盐岩地层为典型的破碎性地层,岩体破碎过程实质上是一种内能耗散现象,钻头破碎地层生热源项[22]为
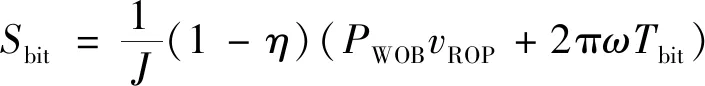
(28)
式(28)中:J为焦耳常数,与所做的功和发热有关;η为钻头效率,在本研究中取0.15;PWOB为钻压,kN;Tbit为钻头上的扭矩,kN/m。
1.2.3 边界条件与初始条件
1)边界条件
(1)钻杆入口温度。进入钻杆的钻井液温度始终保持不变,即
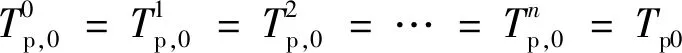
(29)
(2)环空出口压力。由于环空出口与大气直接接触,其出口压力始终为大气压,即
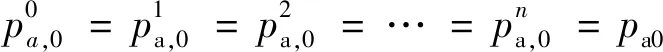
(30)
(3)井底温度和井底压力。钻杆内钻井液的温度和压力与环空钻井液的温度和压力相同,即
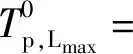
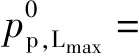
(31)
2)初始条件
钻井开始时井筒内的温度和压力分布称为初始条件。因此,地层温度可作为初始井筒温度,而静液柱压力可作为初始井筒压力,即
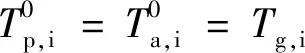
(32)
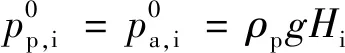
(33)
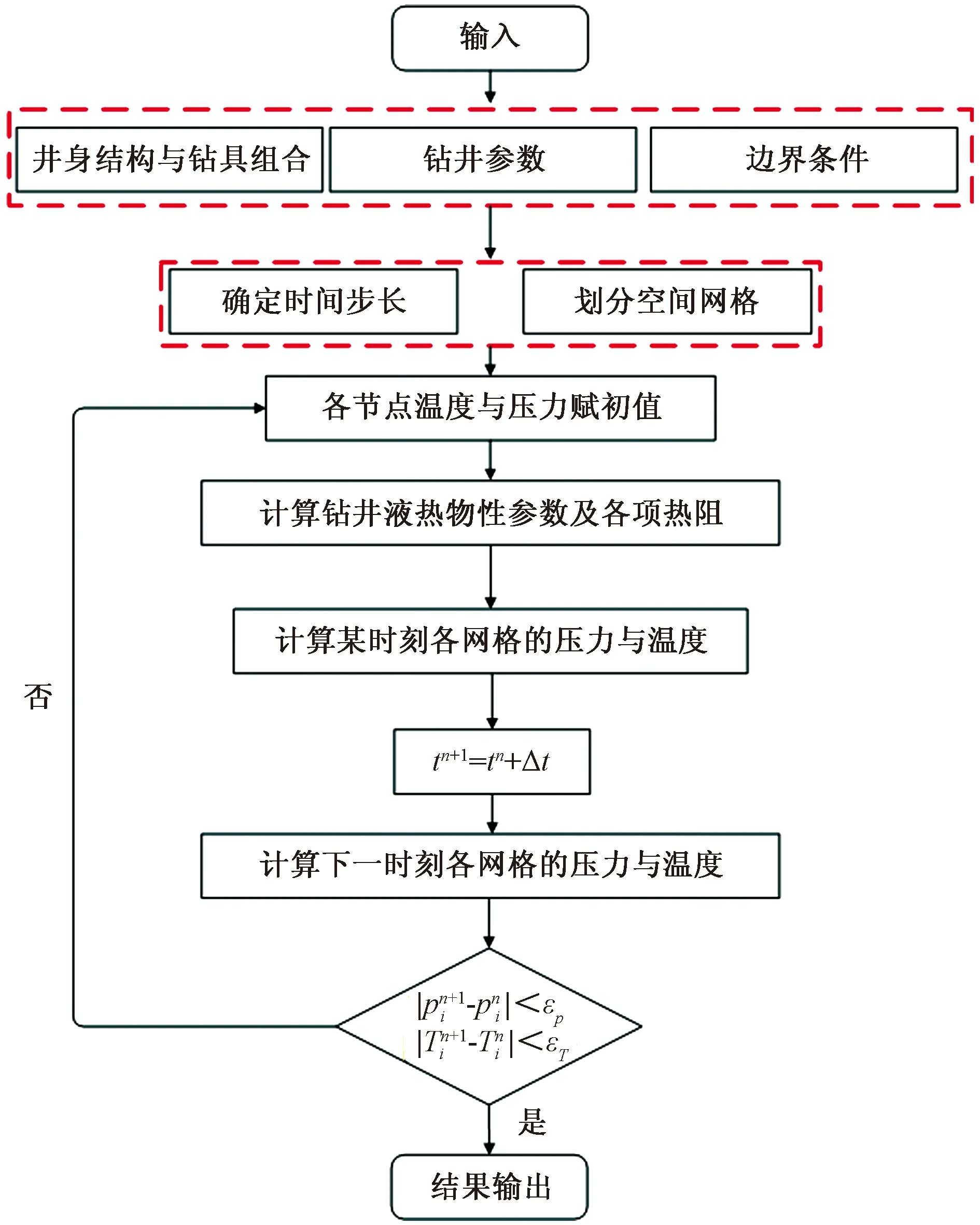
分别为计算的各网格压力及温度分布;分别为假设的各网格压力及温度分布;εp为压力计算精度,本文中取1 Pa;εT为温度计算精度,本文中取0.01 ℃图2 计算流程图Fig.2 Flow chart of the model solution process
2 模型求解及验证
2.1 模型求解流程
采用全隐式有限差分法对上述数值模型进行离散,网格划分示意图可见图1。其计算流程如图2所示,计算步骤如下:①输入井身结构、钻具组合、钻井参数及边界条件;②确定网格尺寸及时间步长;③假设温度及压力的初始分布;④利用物性参数定量描述模型确定初始时刻各网格的物性参数并求出各项热阻;⑤计算各网格新时刻的温度与压力分布,此温度作为下一步的初始条件;⑥重复步骤③~⑤,直至收敛或计算至要求时间为止。
2.2 模型验证
为了验证井筒瞬态传热模型的可靠性,以彭州6-3D水平井实测循环温度对模型进行验证。在彭州6-3D水平井钻井过程中,利用旋转导向系统的井底MWD实测了井深5 700~6 707 m的循环温度。彭州6-3D水平井井身结构见表1所示。该井设计垂深5 725 m,斜深7 363 m。地表温度为16 ℃,平均地温梯度0.023 ℃/m。三开采用强封堵白油基钻井液滑动钻进,钻井液密度1.55 g/cm3,塑性黏度52 mPa·s,动切力11 Pa,钻井液排量20 L/s。
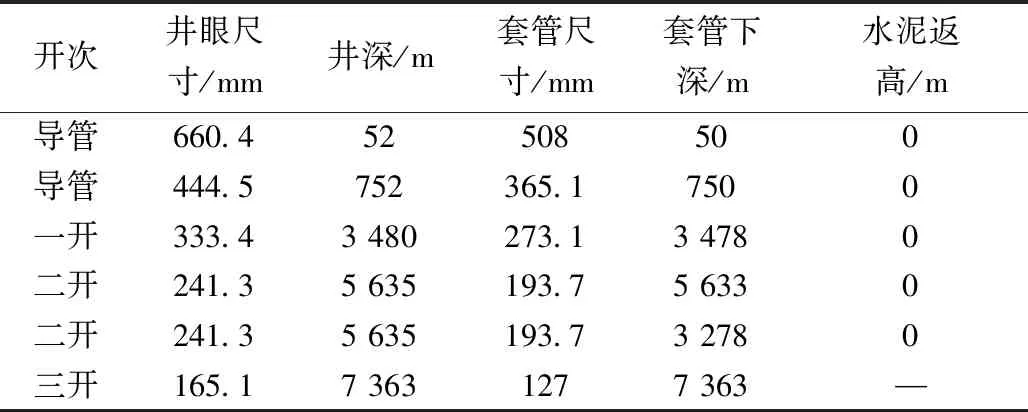
表1 彭州6-3D水平井井身结构Table 1 Basic parameters of the drill string assembly and casing program of Pengzhou 6-3D well
三开采用的钻具组合为:Φ165.1 mm聚晶金刚石复合片钻头+旋转导向工具+钻具回压阀×2个+Φ101.6 mm无磁承压钻杆×1根+Φ101.6 mm钻杆+Φ101.6 mm加重钻杆×30根+Φ121 mm随钻震击器×1个+Φ101.6 mm加重钻杆×15根+钻具旁通阀×1个+Φ101.6 mm钻杆+Φ139.7 mm钻杆×3 200 m。
以地面温度为基准,查得除钻井液以外的相关物性参数见表2所示。

表2 计算所用物性参数Table 2 Thermal physical parameters of different media
该井在井段5 700~6 707 m正常钻进过程的钻井液实测循环温度与计算温度如图3所示。
从图3可知,除随钻测量工具刚投入使用的初期外,所有实测值均在计算值±5%的误差范围内,客观上证实了本研究建立模型的精确度和有效性。

图3 现场测试结果与计算结果的对比Fig.3 Well bottom circulation temperature and field test value comparison
2.3 典型曲线分析
本文所建模型比先前模型的优势在于考虑了各种热源项对钻井过程中的井下温度分布的影响。图4展示了不考虑热源、仅考虑流动摩阻及考虑多热源3种情况下的环空钻井液温度随井深分布的典型曲线。
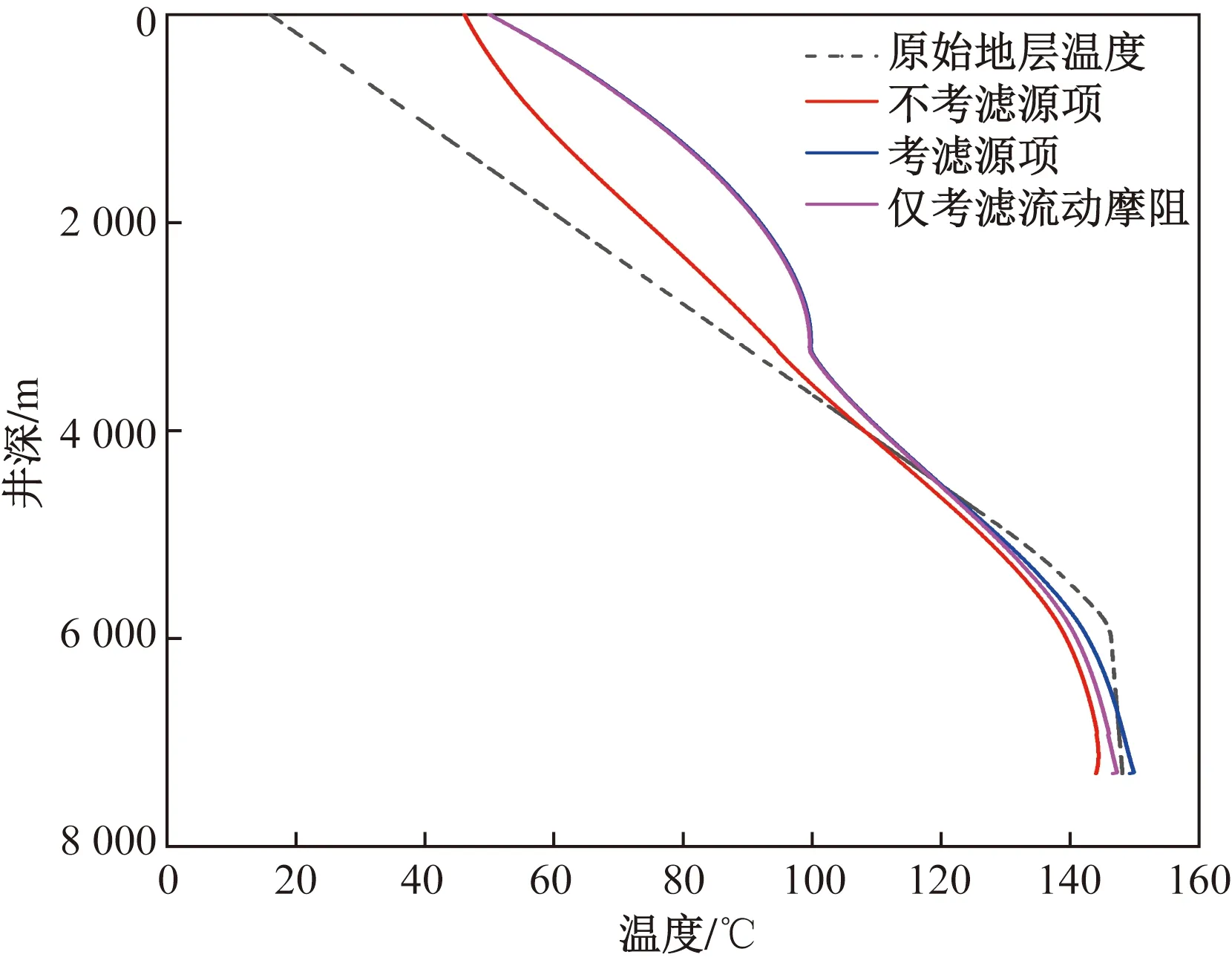
图4 热源对环空钻井液温度分布的影响Fig.4 Effect of the heat source of the drilling fluid on the annulus temperature distribution
从图4可知,考虑多热源影响的井底温度为149.27 ℃,而不考虑源项影响的井底温度为146.66 ℃,两者有2.6 ℃的差距。若仅考虑流动摩阻生热,井底温度为148.14 ℃,与考虑多热源相比也有1.1 ℃的差距。这说明岩石破碎、钻柱旋转、钻头节流及钻杆与井筒之间摩擦产生的热量,同流动摩阻生热一样均不容忽视。
此外,图4中可以观察到洋红色曲线和蓝色曲线均有一明显拐点,而红色曲线却无拐点。这是钻具组合发生变化的缘故,在彭州6-3D三开水平段钻进过程中,上部采用Φ139.7 mm钻具,而下部采用Φ101.6 mm钻具。上部井筒钻杆尺寸大,环空面积小,流速快。因此,无论是仅考虑流动摩阻还是考虑多源项,生热量均会随着流速的增大而增大;而若不考虑源项,则与流速关系不大。
3 井底循环温度影响因素分析
同样以彭州6-3D水平井的基本参数为依据,各种因素对环空钻井液温度分布影响如下。
3.1 水平段长度
根据井眼轨迹设计,此井A靶点井深5 923.48 m,此后开始水平段钻进。图5显示了循环1 h后,不同水平段长度对应的环空钻井液温度分布曲线。
从图5可知,对于6 100 m(水平段长度约200 m)、6 500(水平段长度约600 m)、6 900(水平段长度约1 000 m)及7 300 m(水平段长度约1 400 m)井深,计算得出的井底温度分别为140.49、144.96、147.44、149.27 ℃。水平段长度对下部井筒的影响远大于对上井筒的影响。在相同的垂深处,水平段长度越长,对应的水平段的温度越高,水平段的增加明显增大了井底温度,但是这种增长幅度会随着水平段长度的增加逐渐减小。出现这种现象的原因在于水平段长度越长,钻井液在水平段井筒稳定的高温环境中流动的时间越长,与周围地层的热量交换越充分,从周围地层吸收的热量越多,因此温度越高。以上分析结果表明,在水平井建井过程中更要密切关注井下高温带来的问题。
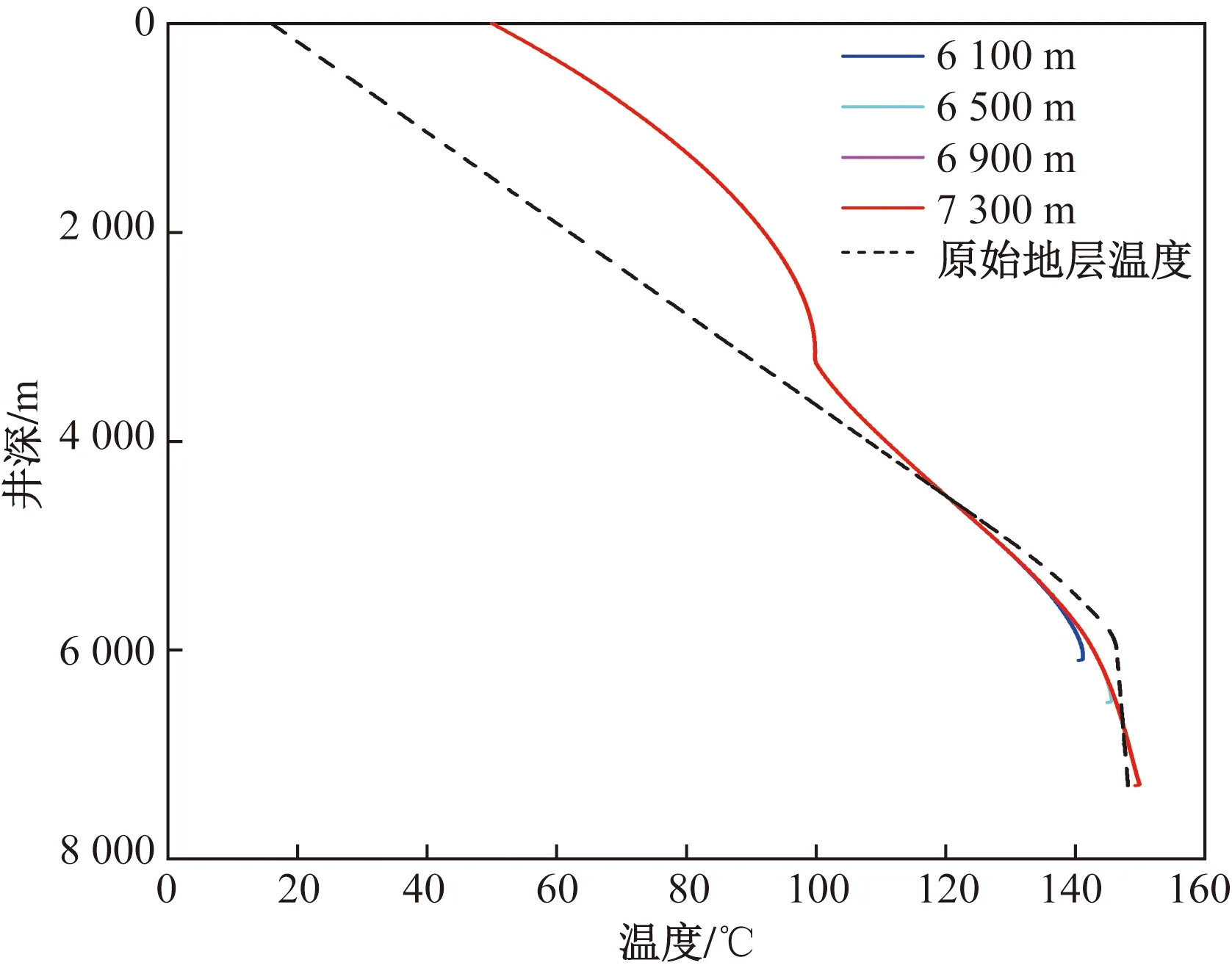
图5 水平段长度对环空钻井液温度分布的影响Fig.5 Effects of horizontal section length on the annulus temperatures distribution
3.2 循环时间
图6显示了钻井液循环时间对环空钻井液温度分布的影响。
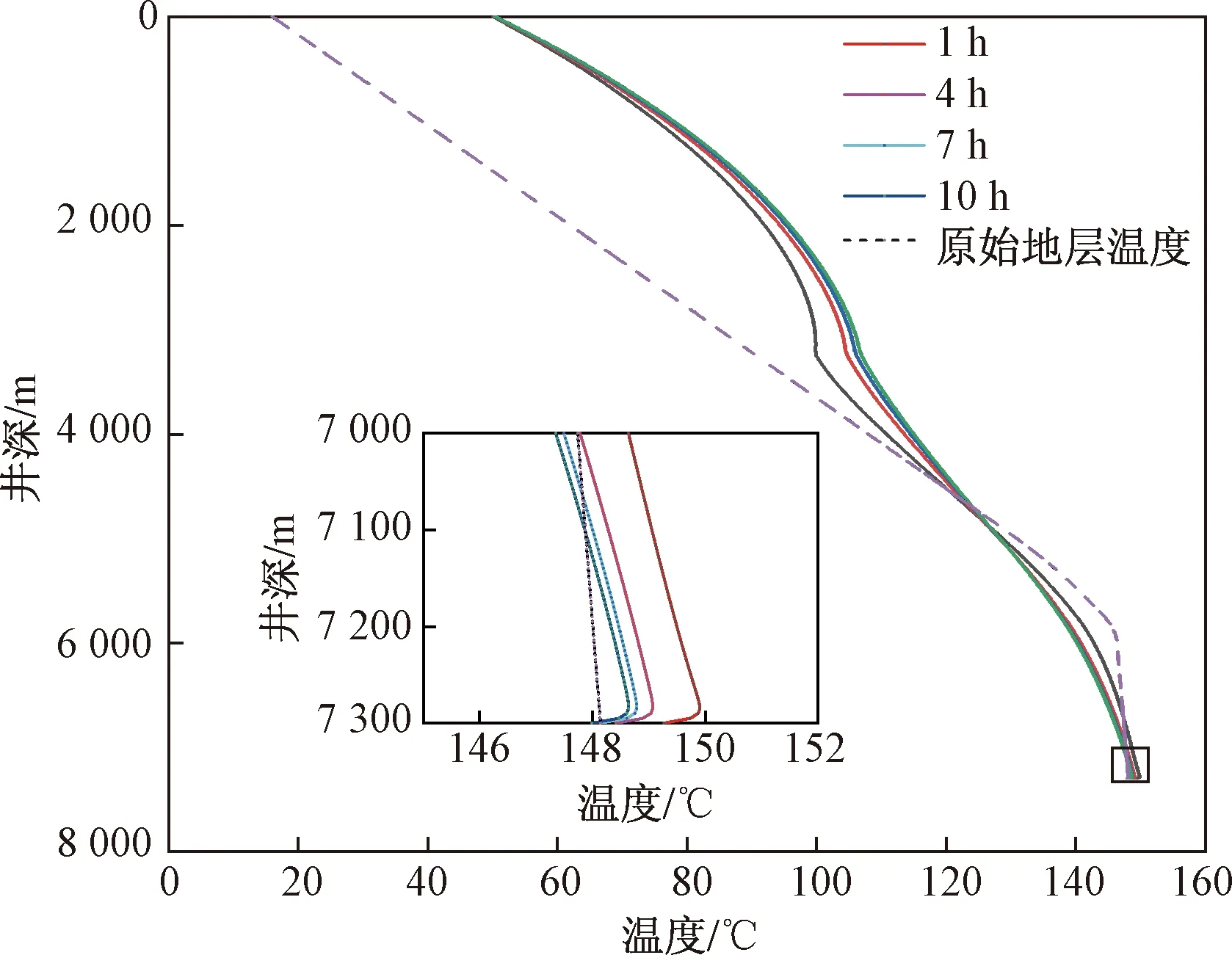
图6 循环时间对环空钻井液温度分布的影响Fig.6 Effects of circulation time on the annulus temperatures distribution
图6表明,井底温度随循环时间的增加而降低;然而,井底温度降低的幅度越来越小。与循环1 h相比,循环4 h时,井底温度从149.27 ℃降至148.42 ℃,井底温度降低0.8 ℃;循环7 h,井底温度再降低约0.3 ℃,循环10 h,井底温度虽继续降低,但仅降低了0.1 ℃。这是因为随着循环时间的延长,地层热阻逐渐增大,钻井液与地层温差减小。因此,从地层到井筒的传热量减少了。根据前述规律,长时间循环对井筒温度分布影响不大。
3.3 循环排量
图7显示了钻井液循环排量对环空钻井液温度分布的影响,可知对于循环排量为10、15、20、25 L/s时,计算得出的井底温度分别为150.54、149.64、149.27、149.49 ℃。这说明在一定的循环排量范围内,随着循环排量的增加,井底温度降低,但下降的速度减小;当流量达到一定阈值时,井底温度不降反升。这是因为本文所建立的模型考虑了多个热源项对井筒温度分布的影响。随着循环排量的增加,虽然单位时间内环空钻井液从地层中带走的热量增加,但各种热源项也相应增加。
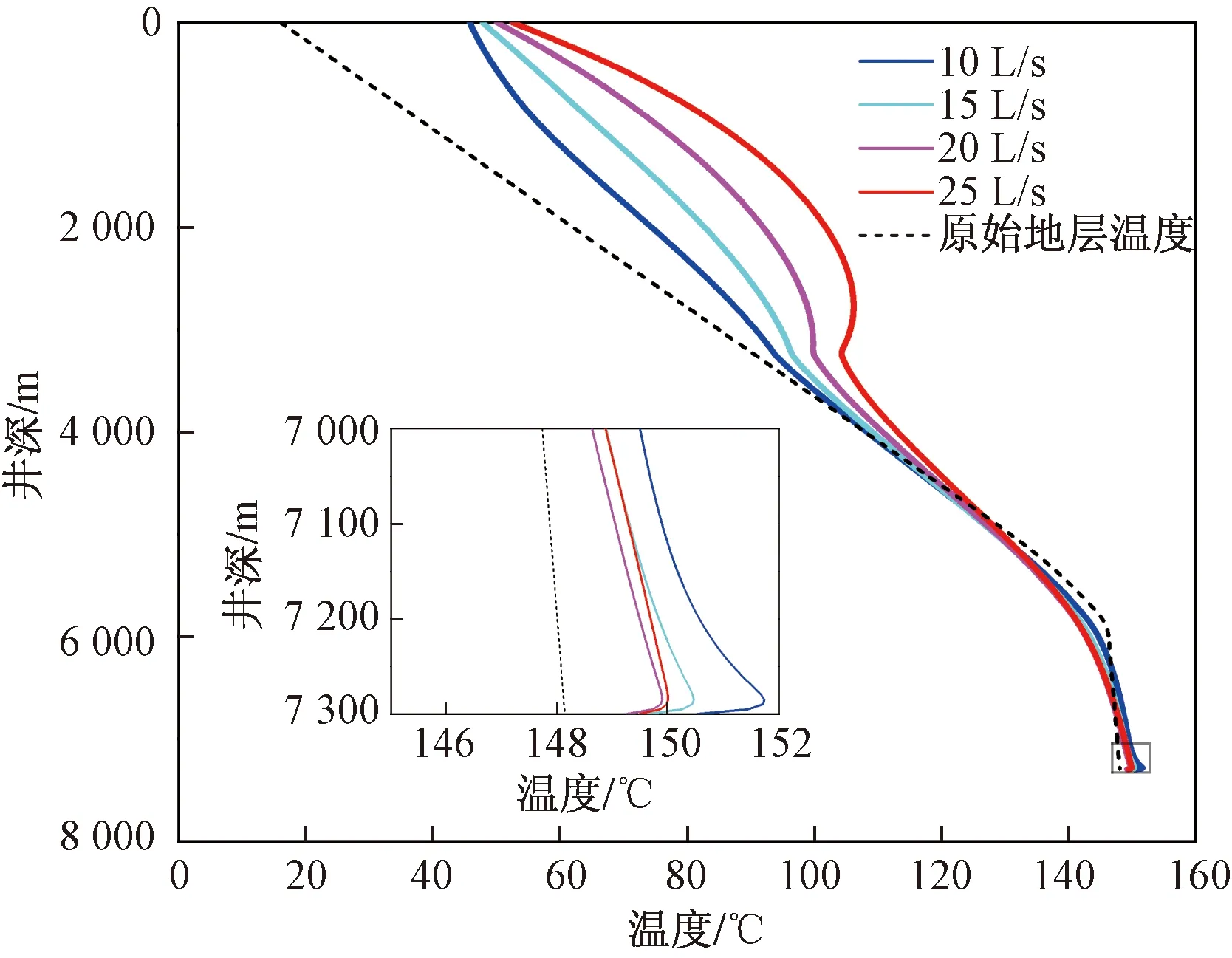
图7 循环排量对环空钻井液温度分布的影响Fig.7 Effects of circulation flow rate on the annulus temperatures distribution
3.4 入口温度
图8显示了钻井液入口温度对环空温度分布的影响。
从图8可知,钻井液的入口温度对上部井筒的影响远大于对下部井筒的影响。当钻井液入口温度为0、15、30、45 ℃时,计算得到的井底温度均在149.30 ℃左右,对应的出口温度分别为9.41、22.75、36.38、50.04 ℃。这是因为在井筒上部,环空中钻井液在向地层传热的同时,也向钻杆内的钻井液传热,钻井液入口温度增加,环空钻井液与钻杆内钻井液温差减小,环空钻井液的热损失量减少,因此,上部井筒环空内钻井液的温度随钻井液入口温度的升高而升高。对于下部井筒,地层持续对环空内钻井液加热,井筒循环温度逐渐升高,地层和环空钻井液、环空钻井液与钻杆内钻井液之间的温差均减小。根据热力学第二定律,三者不会无限制的热交换,其温度将逐渐趋近,这种趋近会随着循环钻井液在井筒中的流动时间的增加而更加明显。因此,下部环空内钻井液温度几乎相同。所以,在深层长水平段钻进过程中使用地面降温系统对降低井底温度作用有限。
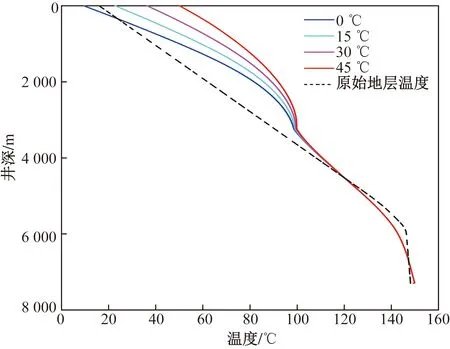
图8 入口温度对环空钻井液温度分布的影响Fig.8 Effects of inlet temperature on the annulus temperatures distribution
4 结论
(1)本文建立的深层碳酸盐岩地层长水平段钻井井筒温度分布模型充分考虑了井身结构、多热源项、钻井液物性随温压变化等多种因素,与现场实测温度误差小于5%,可进行深层碳酸盐岩地层长水平段钻进过程中的井底温度预测。
(2)水平段长度越长,井底温度越高。在水平井建井过程中须密切关注井下高温带来的问题。
(3)增加循环时间、增加循环排量、降低钻井液入口温度等措施对降低井底温度的作用有限。为保障深层碳酸盐岩油气资源开发的顺利进行,需选择满足温限要求的旋转导向工具。
