安装高度及角度偏差对应答器作用距离影响研究
2023-03-14张鑫奎李建国薛千树
张鑫奎,李建国,薛千树
(1.兰州交通大学自动化与电气工程学院,兰州 730070;2.四电BIM工程与智能应用铁路行业重点实验室,兰州 730070)
引言
应答器作为实现车-地通信的点式数据传输设备,具有效率高、信息量大等优点,广泛应用于我国CTCS(Chinese Train Control System)-2、CTCS-3线路和城市轨道交通,为列车运行控制和调度指挥提供及时必要的信息,但应答器安装于室外开阔环境,空间电磁干扰、列车运行中振动与冲击等因素影响数据传输的可靠性与安全性[1-4]。
国内外学者针对应答器系统传输性能做了大量研究,GENG Q等[5]采用数字孪生技术分析了车载天线与应答器之间的能量和数据传输过程;李正交等[6]建立下行链路传输等效阻抗模型,提出阻抗测量与误差校正方法;王通、梁迪等[7-8]基于电磁感应原理,分析了应答器系统数据传输过程与旁瓣感应电压幅值包络问题;付连著、ZHAO L H等[9-11]对高速运行条件下信号系统的适应性及可靠性进行研究评估;李雪等[12-13]结合粒子群算法对应答器传输系统天线在不同周长下的长宽比进行了优化,对应答器角度偏差进行了一致性评估;赵会兵等[14]研究了空间介质对应答器传输系统“A”接口性能的影响;龚水清等[15]对冷、热备天线与BTM(Balise Transmission Module)天线间的最小安装距离进行了研究;张友鹏等[16]等提出基于EEMD的应答器上行链路信号处理方法;LÜ等[17]针对应答器信号噪声干扰,提出基于认知控制的应答器上行链路信号处理方法。
应答器系统传输性能易受安装高度及角度偏差的影响,有必要在不利安装高度与角度偏差同时存在时对应答器作用距离进行深入研究。本文基于电磁场基础理论,建立应答器天线空间磁场分布、BTM天线接收上行链路信号幅度模型,分析了应答器安装高度及角度偏差对应答器作用距离的影响,给出工程安装优化参数,为现场施工与维修提供借鉴,为电磁干扰、速度等影响其传输性能的研究提供基础。
1 应答器系统工作原理
应答器传输系统各设备间通过不同接口连接,车-地信息传输过程[18-20]包括下行激励和上行发送两个过程:BTM天线向地面连续发送27.095 MHz高频电磁能量,当列车经过应答器上方时,通过电磁耦合激活地面应答器,将存储在地面应答器中的数据报文发给BTM天线,通过BTM解码后将信息传给车载计算机,应答器传输系统结构如图1所示。
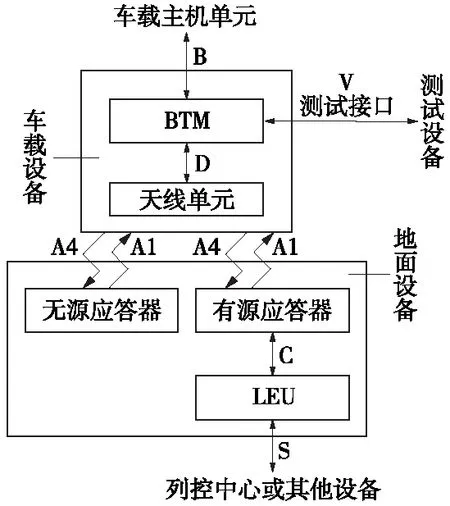
图1 应答器传输系统设备构成
接口“A1”是应答器向车载天线传输数据报文的接口,其信号采用频移键控2FSK(Frequency Shift Keying)调制,载波频率为(4.234±0.175)MHz,频偏为±282.24 kHz,传输速率为564.48 kbit/s,当接收到“0”时,发送载频为3.951 MHz的调制信号,接收到“1”时,发送载频为4.516 MHz的调制信号。
2 模型建立
2.1 应答器天线空间磁场分布模型
应答器参考区域是以Z轴为中心,与应答器X轴和Y轴在相同平面200 mm×390 mm的区域(以标准尺寸为例),应答器位置坐标轴如图2所示。

图2 应答器参考坐标轴(单位:mm)
参考场强是在自由空间中围绕参考区域的恒定电流产生的垂直分量,实际上行链路应答器磁场强度垂直分量与参考场强一致,应答器产生场强与参考场强差值构成上行链路的一致性偏差,根据差值范围将应答器磁场空间分为作用区、旁瓣区和串扰区,串扰区参考场强限制在不超过作用区最高场强衰减范围内,应答器系统磁场作用区定义为上下八角面的柱状型,如图3所示,z0为应答器与BTM天线间的垂直距离。

图3 磁场作用区
地面应答器与BTM天线均为矩形天线,天线周长l与信号波长λ关系为:l<0.159 155λ,应答器系统天线的尺寸与波长相比很小,为电小环天线,天线上电流呈均匀分布,各处电流等幅同相,将应答器天线等效为四段载流线圈,建立天线空间磁场分布模型,如图4所示。

图4 矩形天线磁场计算示意
磁场方向与电流方向形成右手螺旋关系,利用叠加原理求出其空间磁场分布,一段载流直导线在空间某点P(x,y,z)产生的磁感应强度为
(1)
式中,μ0为真空磁导率;I为通过线圈电流;d为P到导线的垂直距离;θ1为∠PDA,θ2为∠PAD(以DA段导线为例),利用公式(1)可精确求解其空间磁场分布。载流直导线AB、BC、CD和DA在Z轴方向的磁感应强度垂直分量分别表示为BABZ、BBCZ、BCDZ和BDAZ,总磁感应强度B在Z轴方向的分量为BZ,式中a=AB/2=CD/2,b=AD/2=BC/2。
BZ=BABZ+BBCZ+BCDZ+BDAZ
(2)
2.2 BTM天线接收上行链路信号幅度模型
建立BTM天线接收上行链路信号幅度模型,反映车-地天线间相对位置关系,如图5所示。建立对称坐标,方便仿真分析,设应答器天线ABCD的边长分别为2l1和2l2,BTM接收天线的边长为2l3和2l4,以应答器天线为激励天线,计算BTM天线接收到的磁通量。
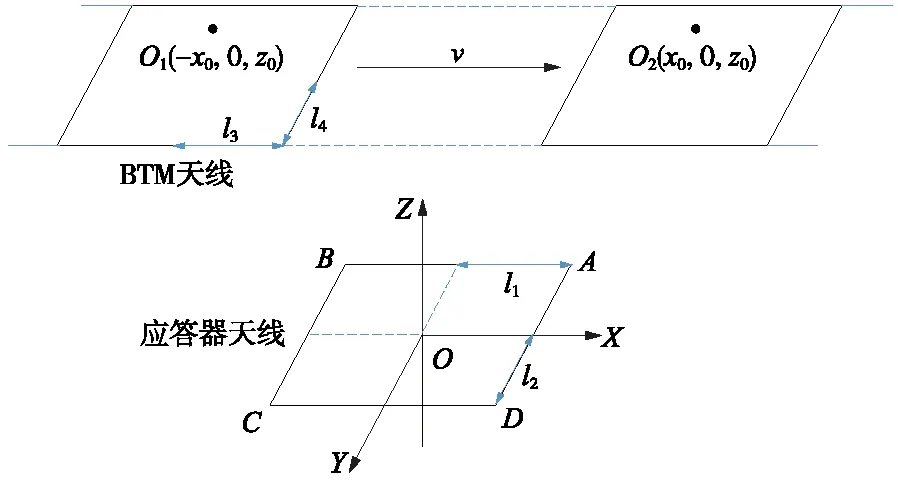
图5 BTM天线接收上行链路信号模型
BTM天线在Z=z0平面内沿着X轴从-x0平移到x0,计算每一位置穿过BTM天线的磁通量,磁通量Φ是磁感应强度在曲面面积上的积分,有

(3)
式中,Σ为BTM接收天线在Z=z0平面上所围的区域;a=l1,b=l2。
由电磁感应定律可得
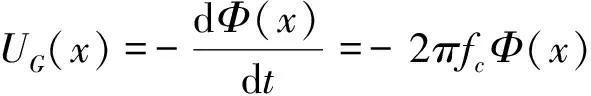
(4)
式中,UG(x)为BTM接收天线上的感应电动势;fc为4.23 MHz。
BTM天线通过谐振回路放大后实际接收到的信号是
U(x)=Q×UG(x)
(5)
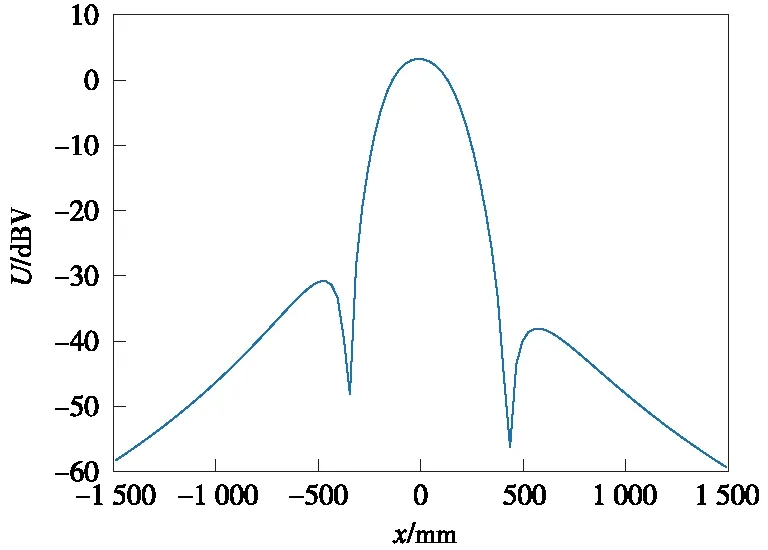
根据应答器现场实际使用情况,结合式(1)~式(5),代入相关参数:μ0=4π×107T·mm/mA,I=180 mA,z0=220 mm,x0=1 300 mm,a=195 mm,b=100 mm,l3=187 mm,l4=218 mm,fc=4.23 MHz,Q=40(纵向安装为例),得到BTM接收到的上行链路信号幅度曲线如图6所示。
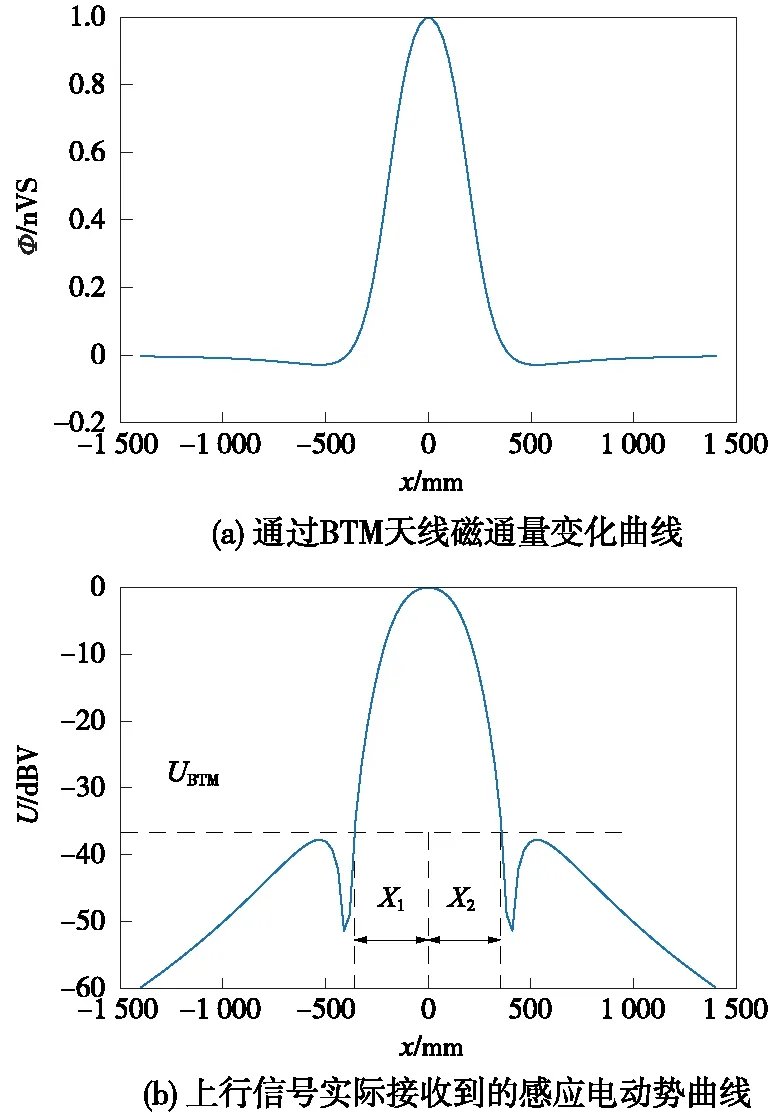
图6 BTM接收到的上行链路信号幅度曲线
UBTM为BTM阈值电压,以应答器中心为原点,将其作用区范围分为左右两段。
2.3 应答器角度偏差数学模型
建立应答器安装角度偏差数学模型,分析角度偏差对应答器作用距离的影响。
2.3.1 应答器倾斜
将应答器天线ABCD的X轴旋转α度得到A′B′C′D′如图7所示。电流ID′A′=ID′H+IHM+IME+IEA′,ID′H与IEA′在z轴方向产生的磁感应强度为0,故ID′A′=IHE,同理可得,IB′C′=IFG,应答器倾斜α角度后,在空间点P(x,y,z)处Z方向产生的磁感应强度为
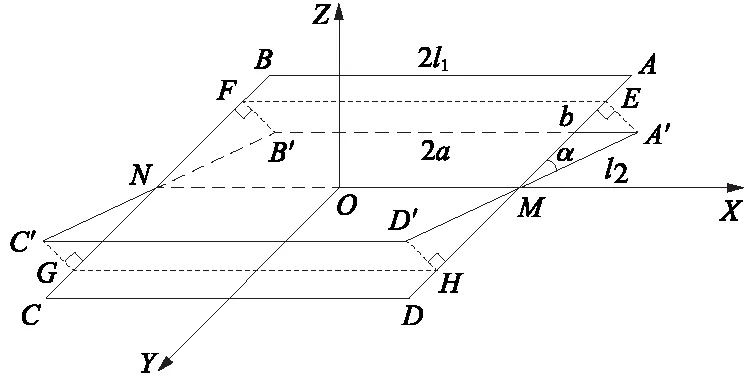
图7 应答器倾斜示意
BZ=BA′B′Z+BB′C′Z+BC′D′Z+BD′A′Z
BA′B′Z=BABZ(x,y,z-l2sinα)
BB′C′Z=BBCZ
BC′D′Z=BCDZ(x,y,z+l2sinα)
BD′A′Z=BDAZ
(6)
式中,a=l1,b=l2cosα。
故通过BTM接收天线的磁通量为
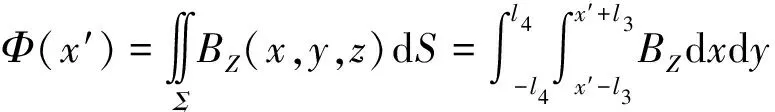
(7)
2.3.2 应答器俯仰
将应答器天线ABCD的Y轴旋转β度得到A′B′C′D′如图8所示。电流IA′B′=IA′E+IEM+IMF+IFB′,因为IA′E和IFB′在Z轴方向的磁感应强度分量为0,所以边A′B′产生的磁感应强度与边EF产生的磁感应强度相等。同理,边C′D′产生的磁感应强度与边GH产生的磁感应强度相等。应答器经过β角度的俯仰后,在空间点P(x,y,z)处Z方向产生的磁感应强度为
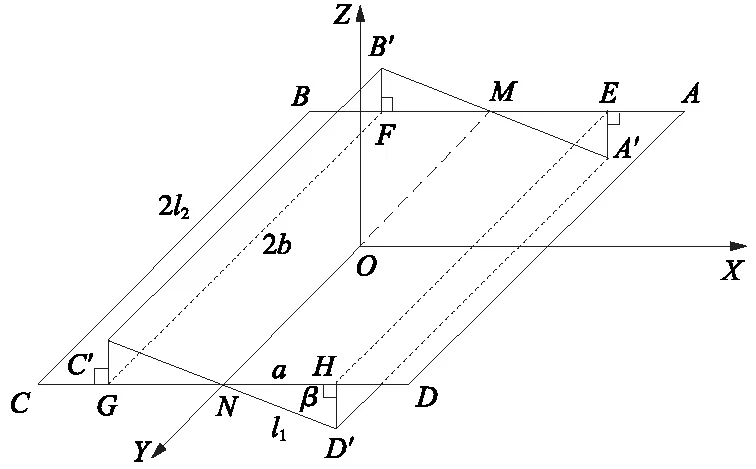
图8 应答器俯仰示意
BZ=BA′B′Z+BB′C′Z+BC′D′Z+BD′A′Z
BA′B′Z=BABZ
BB′C′Z=BBCZ(x,y,z+l1sinβ)
BC′D′Z=BCDZ
BD′A′Z=BDAZ(x,y,z-l1sinβ)
(8)
式中,a=l1cosβ,b=l2。
故通过上行链路接收天线的磁通量为
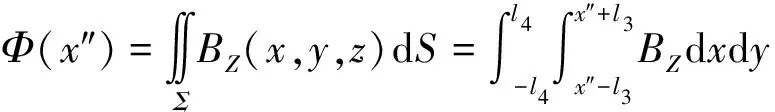
(9)
2.3.3 应答器偏转
将应答器天线ABCD的Z轴旋转γ角度得到A′B′C′D′,如图9所示。俯视应答器,二维直角坐标系中1点(x,y)顺时针旋转γ度后变为2点(x′,y′),1点与2点之间的映射关系为

图9 应答器偏转示意

(10)
应答器经过γ角度的偏转后,在空间点P(x,y,z)处Z方向产生的磁感应强度为
BZ=BA′B′Z+BB′C′Z+BC′D′Z+BD′A′Z
BA′B′Z=BABZ(cosγy′-sinγx′,sinγy′+cosγx′,z)
BB′C′Z=BBCZ(cosγy′-sinγx′,sinγy′+cosγx′,z)
BC′D′Z=BCDZ(cosγy′-sinγx′,sinγy′+cosγx′,z)
BD′A′Z=BDAZ(cosγy′-sinγx′,sinγy′+cosγx′,z)
(11)
故通过上行链路接收天线的磁通量为

(12)
3 仿真实验与结果分析
3.1 不同安装高度仿真
结合式(1)~式(5),代入相关参数,仿真z0=220~460 mm之间BTM收到上行链路信号幅度曲线如图10所示,分析不同高度下应答器作用距离变化情况。
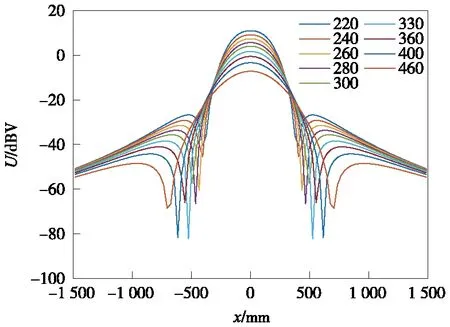
图10 不同z0下BTM收到上行链路信号幅度曲线
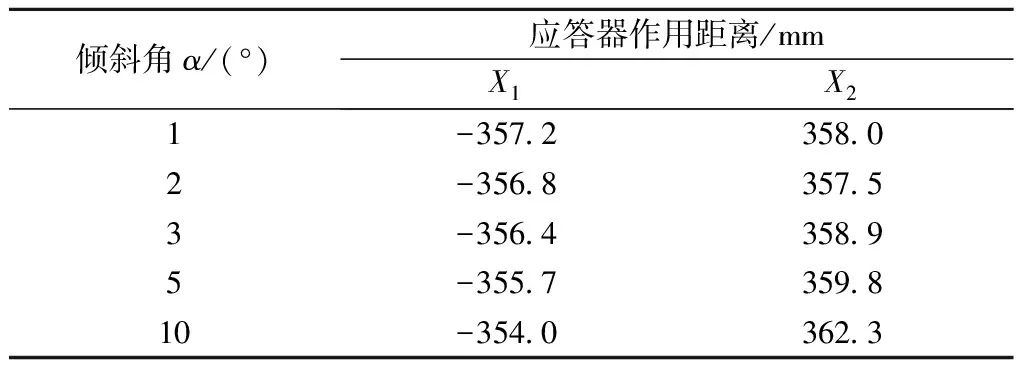
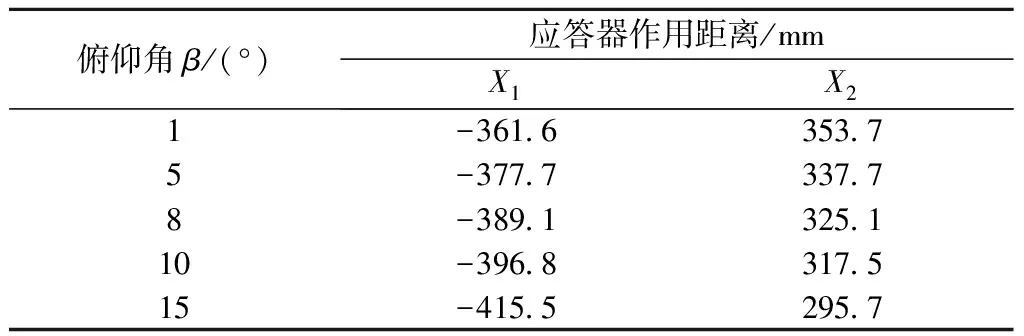
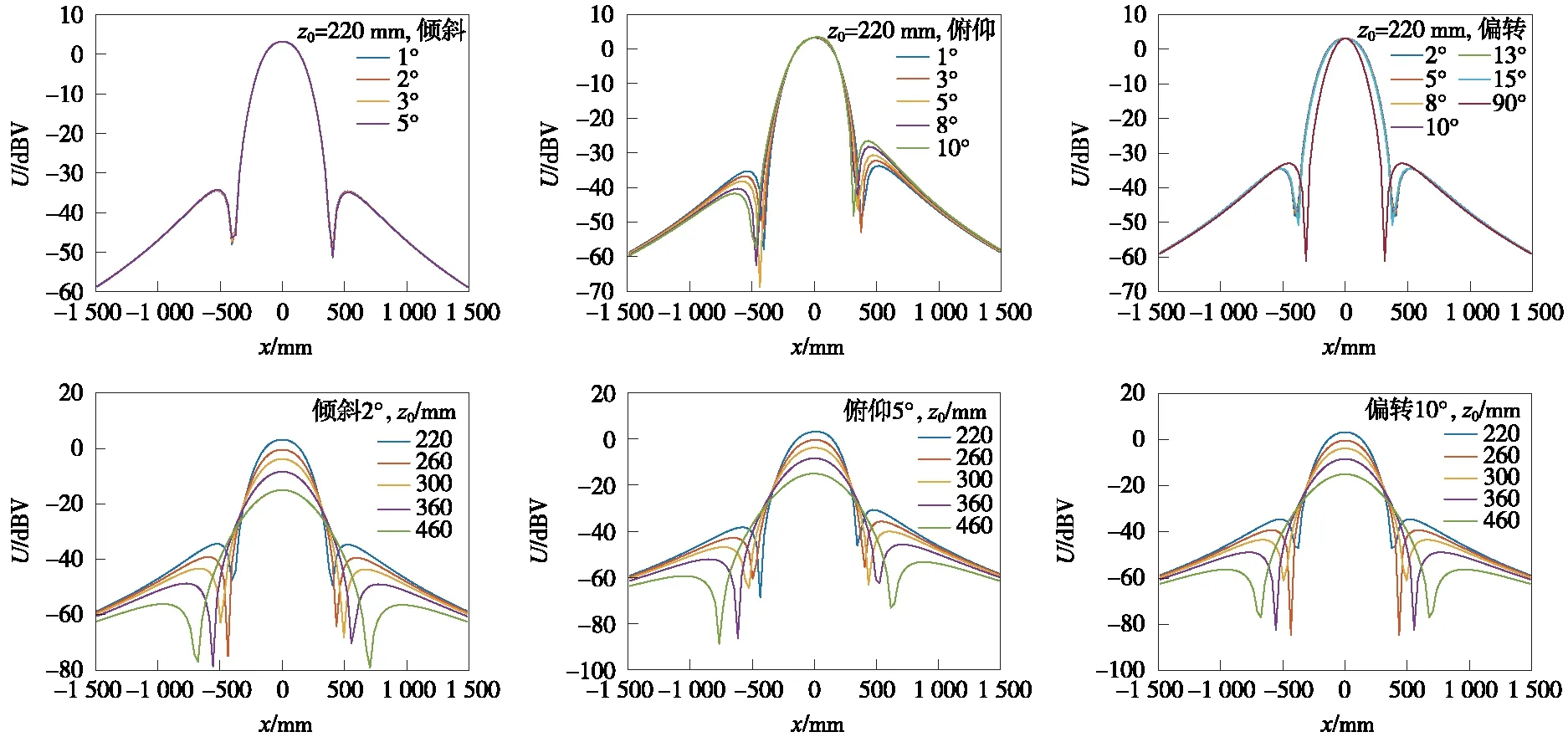
BTM天线与应答器之间的垂直距离z0满足:+220 mm 为抑制旁瓣区、串扰区和其他信号源带来的干扰信号,BTM需设置阈值电压UBTM(由设备厂商设定),当UBTM一定时(以北信公司为例,UBTM对应电流IBTM=51 mA),应答器作用距离随z0的增大先增大后减小,在z0=360 mm附近达到最大值为737.6 mm,不同z0下应答器作用距离变化见表1。 表1 不同z0下应答器作用距离 mm 3.2.1 倾斜角偏差 结合式(1)~式(7),代入相关参数仿真z0=280 mm时,不同倾斜角α下BTM收到的上行链路信号幅度曲线如图11所示,应答器作用距离变化如表2所示。 由图11与表2可得,当应答器发生倾斜(1°~10°)时,应答器作用距离X1从-357.2 mm递增到-354.0 mm,X2从358.0 mm递增到362.3 mm,应答器作用距离变化范围在5 mm以内。 图11 不同α下BTM收到上行链路信号幅度曲线 表2 不同α下应答器作用距离 3.2.2 俯仰角偏差 结合式(1)~式(5)、式(8)、式(9),代入相关参数,仿真z0=280 mm,俯仰角β在0°~15°间BTM收到上行链路信号幅度曲线如图12所示,应答器作用距离变化如表3所示。 图12 不同β下BTM收到上行链路信号幅度曲线 表3 不同β下应答器作用距离 由图12与表3可得,当应答器发生俯仰(1°~15°)时,应答器作用距离X1从-361.6 mm递减到-415.5 mm,X2从353.7 mm递减到295.7 mm,X1与X2受影响程度分别超过50 mm和58 mm,对应答器数据传输产生影响。 3.2.3 偏转角偏差 结合式(1)~式(5),式(10)~式(12),代入相关参数仿真z0=280 mm,γ在0°~90°间BTM收到上行链路信号幅度曲线如图13所示,应答器作用距离变化如表4所示。 图13 不同γ下BTM收到上行链路信号幅度曲线 由图13、表4可得,应答器未发生角度偏差时作用距离为715.2 mm,发生偏转(1°~90°)时,应答器作用距离从714.8 mm递减到600.8 mm,偏转90°时为横向安装,可得纵向安装时应答器平均作用距离比横向安装大114.4 mm。 表4 不同γ下应答器作用距离 3.2.4 高度与角度偏差同时存在仿真分析 结合式(1)~式(12),代入相关参数仿真z0=220 mm,不同倾斜角、俯仰角、偏转角下与偏差角度一定时,不同安装高度下BTM收到上行链路信号幅度曲线如图14所示,应答器平均作用距离变化如表5所示。 表5 高度与角度偏差同时存在应答器作用距离 图14 不同安装高度与角度偏差下BTM收到上行链路信号幅度曲线 应答器发生倾斜1°~3°,俯仰1°~8°,偏转1°~15°,z0=220 mm比z0=280 mm应答器平均作用距离分别减小44.7,45.1,45.9 mm,倾斜2°,俯仰5°相比无角度偏差在不同z0下平均作用距离变化在0.1 mm范围内,偏转10°相比无偏转作用距离减小7.0 mm。 仿真z0=220 mm,倾斜2°,俯仰5°,偏转10°时BTM收到上行链路信号幅度曲线如图15所示。 图15 高度角度偏差同时存在时上行链路信号幅度曲线 通过计算得到z0=220 mm,倾斜2°,俯仰5°,偏转10°时应答器作用距离为663.2 mm,比z0=280 mm平均作用距离减小49.8 mm,相比无角度偏差时减小45.1 mm。在静态条件下,应答器发生倾斜、俯仰比无偏差时应答器作用距离变化幅度微小,发生偏转时不同z0与其关系如表6所示。 表6 不同z0与偏转角偏差基本要求 BTM天线与应答器垂直距离z0越小,所容许偏转角偏差越小,应答器发生反方向角度偏差与其相同。在实际运行环境下,应答器作用距离不得小于0.6 m,由于空间电磁干扰等因素的影响,严格控制应答器安装条件将风险降到最低。 通过分析应答器传输系统天线间的耦合原理,建立矩形天线磁场分布、角度偏差理论模型,仿真BTM接收上行链路信号幅度曲线,计算分析得出以下结论。 (1)BTM天线与应答器间垂直距离z0越大,作用区、旁瓣区磁场强度越小,BTM阈值电压一定,作用距离随z0的增大先增大后减小,当z0=360 mm时作用距离最大为737.6 mm。 (2)在静态条件下倾斜角偏差对应答器作用距离影响不大,应答器俯仰角偏差越大,X1区作用距离越大,旁瓣区磁场强度越小,干扰越小;X2区作用距离越小,旁瓣区干扰越大,偏转角偏差越大,应答器作用距离越小,相比纵向安装,横向安装应答器平均作用距离减小114.4 mm。 (3)安装高度与角度偏差同时存在时,应答器发生倾斜、俯仰对其作用距离影响甚微,发生偏转时比无偏差平均作用距离减小7.0 mm,静态条件下,安装高度比角度偏差对应答器作用距离影响程度大。z0越大,所容许偏转角偏差越大,偏转角偏差在(-11.41°,11.41°)范围内时应答器作用距离受影响较小。 本文得出的结论对现场作业具有指导意义,但在文中研究只考虑安装高度角度偏差,未考虑其他风险因素,今后将对列车运行速度、电磁干扰等因素影响应答器传输性能进行研究分析。
3.2 不同角度偏差仿真






4 结论
