高铁CPⅡ控制网BDS/GPS快速测量对比试验分析
2023-03-14潘佩芬黄丁发
李 进,冯 威,潘佩芬,黄丁发
(1.西南交通大学地球科学与环境工程学院,成都 611756;2.中国铁道科学研究院集团有限公司电子计算技术研究所,北京 100081)
引言
近年来,我国铁路的改革与发展已取得举世瞩目的成就,高速铁路成为了我国的亮丽名片。随着“八纵八横”高铁网建设的全面展开,截至2021年底,我国高速铁路运营里程已超过4万km[1]。TB 10601—2009《高速铁路工程测量规范》[2](以下简称“《规范》”)是高铁建设、维护、运营的保障,当前GNSS技术已在高速铁路控制测量中被广泛应用。2020年7月31日,新一代北斗卫星导航系统(BeiDou Navigation Satellite System,BDS)开始正式服务于全球[3-4],丰富了GNSS多星座的组成,为高速铁路控制测量提供了更好的观测基础[5-6]。因此,有必要通过缩短《规范》中所要求的观测时长来提高GNSS高速铁路控制测量的作业效率,而将观测时长缩短为多长能满足《规范》中GPS要求时长所达到的精度,成为当前亟待研究与探索的课题。
目前,已有学者对BDS/GPS解算模型进行了研究,ODOLINSKI等[7-10]利用GNSS观测数据研究了GPS/BDS短基线相对定位,结果表明短距离情况下BDS定位精度及可靠性与GPS相当,融合GPS+BDS定位精度优于任一单系统;吕金浩等[11-13]对BDS和GPS相对定位精度分析发现,BDS卫星几何分布强度不如GPS,定位精度稍逊于GPS,BDS/GPS组合系统的定位精度和稳定性要比单一系统更优;王阳[14]等定量分析了观测时长对短基线解算精度的影响,4 h观测时长下的解算精度优于10 mm;周乐韬[15]等分别通过实测数据对BDS-2和仿真数据对BDS-3相对定位精度分析发现,BDS-2在其服务区内精度总体上与GPS相当,BDS-3在亚太地区定位精度高于GPS;严丽[16]等利用单BDS观测数据进行了CPⅠ控制网数据处理试验,结果表明精度能够达到与GPS相当的水平,满足高铁CPⅠ控制网的建设要求,能够在高铁CPⅠ控制网的建立方面得到广泛应用。
上述研究大多基于BDS-2进行,随着BDS-3的建成开通,以包含BDS-3的GNSS多星座为主建立控制网成为必然趋势,以往针对控制测量观测时长对其精度影响的研究甚少。首先,基于GPS、GPS+BDS卫星可用性分析了全球PDOP值的变化情况;利用某高铁线路CPⅡ控制网的观测数据,根据基线解算模型估算出GPS、GPS+BDS短基线相对定位精度随观测历元的变化趋势;利用自编软件根据GPS、BDS、GPS+BDS不同组合解算模式分析自BDS-3正式运行后在控制测量中的贡献;为提高控制测量效率,针对缩短《规范》要求的观测时长能否满足高速铁路控制测量中的应用,对控制网观测时长从60 min缩短到5 min进行基线解算及无约束网平差,并依据《规范》对控制网成果的各项评定指标进行分析。
1 GPS/BDS可用性与解算模型
1.1 GPS/BDS可用性分析
位置精度因子(Position Dilution of Precision,PDOP)是衡量卫星定位精度的一个重要指标,不仅与卫星在空间的几何构型有关,还与所观测到的卫星数目相关。设有未知参数的协因数阵为

(1)
易求得PDOP=qxx+qyy+qzz[17-19]。
利用全球卫星的可见性,计算GPS与GPS+BDS的全球1°×1°格网点的PDOP值。图1显示了GPS卫星全球的星座瞬时PDOP值变化情况,对于中国区域而言,PDOP值存在明显的变化幅度,分布在1.7~2.9内。融合BDS后的星座瞬时PDOP值如图2所示。

图1 GPS卫星星座瞬时PDOP值(高度角≥15° 2021/07/02/01:00 GPST)

图2 GPS+BDS卫星星座瞬时PDOP值(高度角≥15° 2021/07/02/01:00 GPST)
可以看出,在BDS加入后PDOP值明显降低,在中国区域内降低到1.0~1.3,变化幅度小,趋于稳定。综上可知,融合 BDS 后多星座观测条件得到了改善,观测卫星数增多,星座间空间异构性变好,进而PDOP值降低,说明在GNSS控制测量时采用多星座的观测数据质量将高于单GPS的数据质量。可认为在GNSS控制测量中,当相对定位精度一定,采用GPS+BDS多星座的观测时长将优于单GPS测量。
1.2 GPS/BDS解算模型
基线解算中常采用双差模型,该模型不仅能消除接收机与卫星钟差,还能削弱其传播路径的影响[20]。其观测方程为

(2)
式中,Δ∇为双差运算算子;φ为载波相位观测量;j、k为卫星号;m为基准站;n为流动站;ρ为站星间距离;I为电离层延迟;T为对流层延迟;λ为波长;N为整周模糊度;P为伪距观测量;ε和e分别为载波相位与伪距观测量噪声。在短基线处理时,双差可使两测站受到的对流层与电离层折射误差消除,其余传播路径误差可认为近似相同。由于BDS与GPS存在系统间偏差,当同步观测到BDS和GPS卫星颗数分别为m、n时,可组成m+n-2个观测方程,简化为
V(m+n-2)×1=AX-L
(3)
其中

(4)
式中,a为流动站坐标改正数系数矩阵;b=diag(-λ),转换为只含X的法方程
ATPAX=ATPL
(5)

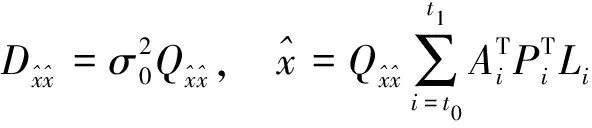
(6)

1.3 观测时长对基线解算的影响
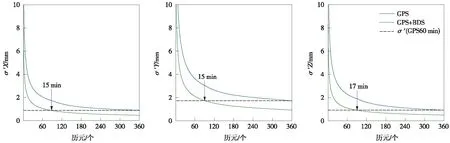
图3 相对定位精度与观测历元个数的关系
2 实验分析
2.1 数据介绍
本次实验数据采用某高铁CPⅡ控制网中由Trimble R12接收机,天线为TRMR12 NONE采集的GNSS实测数据,选取3个观测点组成的3条基线,2个时段的数据进行分析。其CPⅡ控制网对应的精度和技术指标如表1所示,观测时间为2021年7月2日的2个时段,采样间隔为10 s。

表1 CPⅡ控制网精度和技术指标
3条基线第1个时段的共视卫星数量如图4所示,可以看出3条基线GPS共视卫星为4~7颗,由于BDS-3卫星的出现,BDS卫星数高于GPS卫星为16~21颗,GPS+BDS共视卫星可高达27颗。图5统计了3条基线的卫星PDOP值,可以看出GPS的PDOP值最不稳定,其均值为3;BDS的PDOP值相较于GPS有明显下降,其均值为1.8,两个系统融合的PDOP则进一步降低到了1.2,星座几何构型进一步增强,进而提高定位精度。

图4 基线共视卫星数量统计

图5 基线共视卫星的PDOP值统计
2.2 3种解算模式试验
为分析融合BDS后对多星座GNSS控制测量的影响,利用自编软件根据解算模型按照3种不同解算模式(GPS、BDS、GPS+BDS)进行相对定位的数据处理,统计了第1个时段3条基线向量的N、E、U各方向的偏差,为更直观地表述不同解算系统的差别,图6给出了3种解算组合下平面方向95%的置信度椭圆以及U方向偏差时间序列图。由图6可以看出,GPS+BDS组合的相对定位精度要优于单系统。GPS系统平面方向的定位误差在7.9 mm左右,融合BDS后,定位误差分布在4.3 mm左右,因此,融合BDS可使以往的单系统平面定位精度提升约54%。在高程方向上可以看出,单GPS定位误差分布在18.9 mm左右,融合后误差减少到10.9 mm,其精度提升了57%。不管从平面方向还是高程方向,在GNSS控制测量中加入BDS系统进行相对定位时,基线共视卫星数目得到提高,卫星几何构型得到改善,进而减小了相对定位各方向的误差。
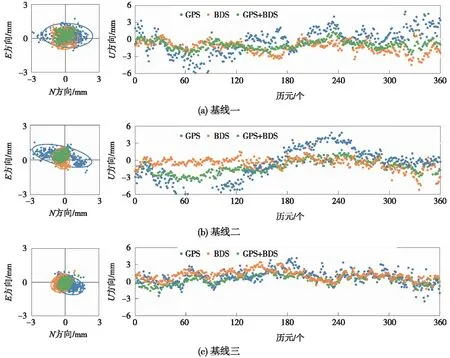
图6 3条基线N、E、U方向定位误差分布
为进一步分析不同组合的相对定位精度,统计了3条基线2个时段3个方向定位误差的RMSE(均方根误差),结果如表2所示。

表2 基线不同组合下N、E、U方向定位误差的RMSE mm
由图2统计结果可知,GPS+BDS在GNSS控制测量中,N、E、U方向的精度较单GPS有大幅度提升,在N方向的RMSE上有50%以上提升幅度,在E方向的RMSE有30%以上提升幅度,在U方向的RMSE有40%以上提升幅度。
2.3 GPS+BDS观测时长分析
由表1可知,在GNSS测量时利用GPS观测时长需观测60 min以上,根据式(5)进行GPS+BDS多星座不同观测时长控制测量试验,分析X、Y、Z方向的中误差σX、σY、σZ、重复基线较差、同步环闭合差是否满足《规范》中的指标。由图3可以看出,在0~15 min内其3个方向精度趋势变化明显,随着时长增加,精度逐渐趋于稳定。以《规范》中要求观测时长60 min的基础上,按5 min间隔逐渐缩短观测时长对该GNSS控制网进行数据处理,得到6条基线的点位精度随着观测时长变化如图7所示。

图7 GPS+BDS不同观测时长基线解算精度
其横坐标为不同的观测时长,纵坐标表示点位精度,水平实线表示《规范》中所要求的最低观测时长60 min采用GPS进行处理得到的点位精度阈值,以此作为评判标准。可以看出,各基线随着观测时长的逐渐缩短,精度逐渐降低,在5~15 min内精度变化明显,综合6条基线而言,分析可知,将GPS+BDS的观测时长缩短为20 min同样能够达到与GPS相同的精度。
另外,统计不同时长的重复基线较差、同步步环闭合差、异步环闭合差合格率为100%,均满足其《规范》中的指标,并且不影响基线解算质量。在基线解算完成后,对构成的基线网进行网平差得到不同时长的无约束平差基线分量的改正数绝对值(VΔX、VΔY、VΔZ)均小于《规范》中要求的VΔ≤3σ。因此,在GNSS控制测量过程中利用多星座进行数据处理时,缩短观测时长为《规范》中的34%同样能够解算全部基线,达到《规范》中要求的精度。
3 结论
针对新一代北斗卫星导航系统对缩短《规范》中要求的观测时长、提高作业效率性能评估开展理论分析与试验研究,结论如下。
(1)根据GPS、GPS+BDS卫星可见性分析了全球PDOP值的变化情况,在我国区域内GPS的PDOP值分布在1.7~2.9,融合BDS后降低到1.0~1.3。推导了基线解算精度随观测时长变化的先验模型,模型表明GPS+BDS采用约16 min的观测时长得到的相对定位精度与单GPS采用60 min的精度相当。
(2)采用某高铁CPⅡ控制网实测数据,分析了构成基线的共视卫星数量、PDOP值变化情况,使用BDS、GPS、GPS+BDS 3种解算模式分析了基线平面和高程方向的定位误差分布情况以及N、E、U方向定位误差的RMSE值,结果表明,GPS+BDS组合解算模式定位精度优于单GPS,在平面和高程方向的定位精度分别有54%、57%的提升幅度。
(3)利用GPS+BDS不同观测时长的数据进行基线解算、网平差,结果表明,融合BDS后在GNSS控制测量中可将观测时长缩短为原来的34%,其定位精度同样能够满足《规范》中CPⅡ控制网的各项精度指标。
随着BDS-3的全球开通,BDS卫星数量的增加丰富了多星座GNSS观测数据,在进行GNSS控制测量时,可以适当缩短观测时长,实现快速测量,提高观测效率。研究成果对《规范》的修订具有一定参考价值。
