城际铁路橡胶浮置板轨道动力特性理论试验研究
2023-03-14李大成
李大成
(中国铁路设计集团有限公司, 天津 300308)
引言
为满足区域经济和城市群内部客运流量日益增长的需求,在城市群中心城市之间、中心城市与其他主要城市间建设快捷融合的城际铁路网十分必要。然而,城际铁路带来的振动和噪声问题,也日益引起人们的重视和关注[1]。
针对轨道交通减振降噪相关问题,诸多学者进行过研究,CAI等[2]通过建立车-轨耦合动力学有限元模型,研究了弹性长枕轨道结构的减振特性,并在北京地铁开展了测试试验[3];李平、朱志辉等[4-5]研究了现浇钢弹簧浮置板轨道的动力特性及随机振动特征;郝晓成等[6]通过试验和数值模拟对地铁减振板式轨道动力和减振特性进行了研究;赵才友等[7-8]通过现场测试试验,研究了橡胶减振垫的减振效果;周鸿[9]提出地铁被动式橡胶垫减振轨道动力特性及设计参数的影响规律;何鉴辞[10]对比分析了聚氨酯减振垫与橡胶减振垫浮置板轨道的动力特性及减振效果;马蒙[11]基于现场测试和定点锤击试验研究了不同激励荷载作用下浮置板轨道的减振效果;刘卫丰[12]通过在北京地铁开展现场测试研究了调频式钢轨减振器的减振降噪效果;战家旺、江万红等[13-14]研究了梯形轨枕轨道的动力特性和降噪效果。既有研究多集中于城市轨道交通及市域轨道交通,对城际铁路研究相对较少。
为研究橡胶浮置板轨道在城际铁路中的适用性,基于理论计算研究了城际铁路橡胶浮置板的动力特性及其减振特性,同时通过落轴冲击测试对橡胶浮置板轨道的减振性能进行试验研究,以期为城际铁路减振轨道结构研究及设计提供参考。
1 车辆-轨道耦合动力学模型
1.1 主要计算参数
以某城际铁路快速轨道交通系统CRH动车组列车[15]为例,设计时速为200 km,轴重17 t。
橡胶浮置板轨道结构主要由钢轨、扣件、轨道板、橡胶减振垫、底座板、回填层组成。钢轨采用60 kg/m钢轨;扣件垂直静刚度为35 kN/mm,动静刚度比取1.4;轨道板为C40混凝土,长4.962 m、宽2.4 m、厚0.19 m,板缝70 mm;底座板为C40混凝土,长5.032 m、宽2.8 m、厚0.2 m;轨道板与底座板间铺设厚30 mm的弹性橡胶垫;橡胶垫刚度有0.019,0.033,0.042,0.1 N/mm3四种。主要材料计算参数如表1所示。
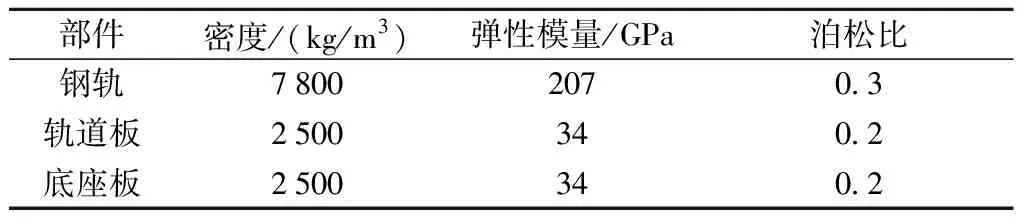
表1 轨道结构材料属性
1.2 模型建立
运用耦合动力学理论,建立城际铁路车辆-橡胶浮置板减振轨道系统动力分析模型,由车辆、橡胶浮置板轨道和轮轨接触模型组成。
车辆模型部分,根据车辆的结构形式、悬挂特性,将车体、转向架、轮对视为刚体,彼此之间通过弹簧阻尼连接组成多刚体系统。模型中,车体和转向架各有5个自由度,每个轮对具有4个自由度,共31个自由度。车辆模型示意如图1所示。
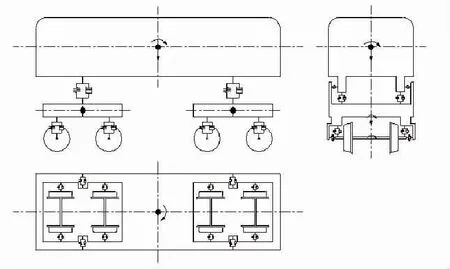
图1 车辆模型示意
轨道结构部分,钢轨采用Euler梁单元模拟,扣件采用线性弹簧模拟,轨道板、弹性垫板、底座板均为实体单元,有限元模型如图2所示。
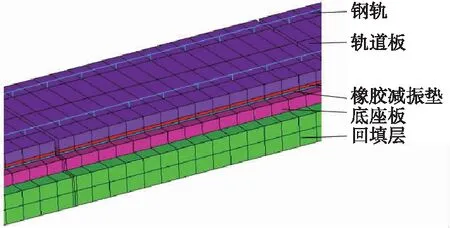
图2 橡胶浮置板轨道有限元模型
将车辆和轨道作为一个联合动力体系,以轮轨接触为界面,分别建立车辆和轨道的运动方程,通过轮轨的几何相容条件和相互作用力平衡条件建立联系。
将车辆和轨道的运动方程联立,得到车辆-轨道耦合系统的运动方程
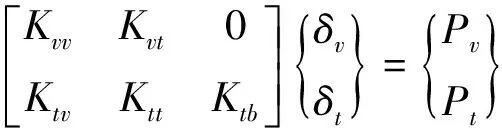
(1)
式中,下标v、t、b分别为车辆、轨道和基础。
求解方程组,可以得到系统各部分的动力响应。车辆和轨道通过轮轨相互作用耦合[16],轮轨法向相互作用采用赫兹非线性接触模型,切向相互作用采用非线性摩擦因数模拟。轨道不平顺如图3所示。
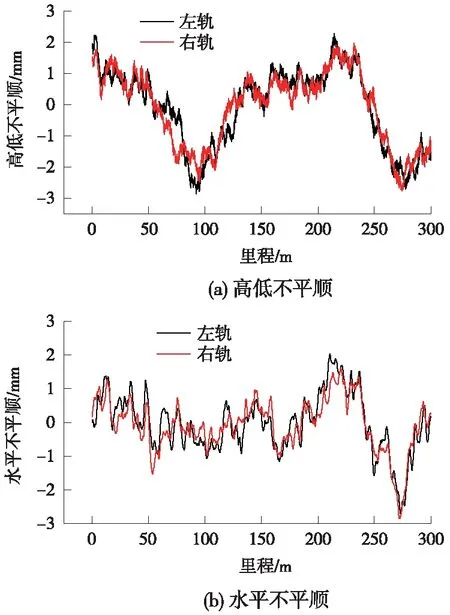
图3 模型中轨道高低及水平不平顺
1.3 模型验证
为验证分析模型的正确性,将本文计算结果与文献[17]进行对比验证。与文献[17]相比,车辆轴重均为17 t,橡胶垫刚度为0.02 N/mm3(文中取0.019 N/mm3≈0.02 N/mm3)。对比行车速度均为160 km/h条件下,钢轨位移、轨道板位移、轨道板加速度等主要计算结果如表2所示。

表2 本文模型计算结果与文献[17]对比
由表2可知,本文与文献[17]的计算结果相近。钢轨位移存在差异的主要原因是扣件刚度不同,而浮置板动力响应主要与浮置板厚度、参振质量相关。总体来看,本文仿真分析结果反映的主要规律与文献计算结果相同,因此,本文所建立的动力学分析模型可用于进一步研究。
2 动力特性分析
2.1 评价指标
CJJ/T 191—2012《浮置板轨道技术规范》[18]规定列车荷载作用下钢轨垂向位移不应大于4.0 mm,轨道板垂向位移不应大于3.0 mm。但对于钢轨、轨道板振动加速度限值目前尚无明确规定。参考TB10761—2013《高速铁路工程动态验收技术规范》[19],确定城际铁路橡胶浮置板减振轨道结构动力学评价指标如表3所示。

表3 轨道结构动力性能评价指标
2.2 结构动位移分析
为研究橡胶浮置板轨道结构动位移能否满足城际铁路轨道几何形位及运行安全要求,以城际铁路设计速度分别为120,160,200 km/h为例,分别计算橡胶垫浮置板轨道钢轨、轨道板动位移,时程曲线如图4所示。
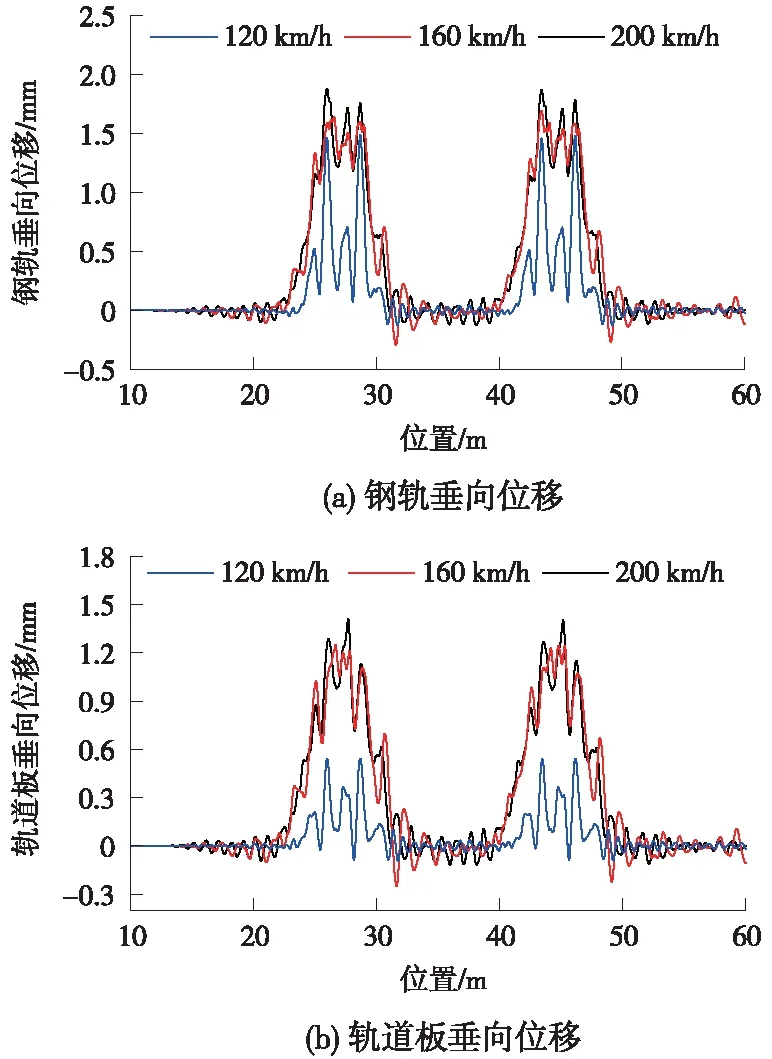
图4 浮置板轨道结构动位移时程曲线
由图4可以看出,在列车动荷载作用下,钢轨、轨道板会产生较为明显的垂向位移。随着车速增大,轨道板垂向动位移增大明显。车速从120 km/h增大到160 km/h,再增大到200 km/h,钢轨垂向位移从1.49 mm增大到1.69 mm,再到1.88 mm,轨道板垂向位移从0.54 mm增大到1.25 mm,再到1.41 mm。可见,设计速度为200 km/h时,钢轨、轨道板动位移均小于允许限值。
对比高速铁路轨道结构位移限值,橡胶浮置板轨道由于铺设了刚度较小的减振垫,轨道结构位移比一般无砟轨道大,但钢轨最大垂向位移仍小于高速铁路一般无砟轨道限值2.0 mm[19],说明橡胶浮置板轨道对城际铁路线路平顺性影响小,满足高速行车条件下线路平顺性要求。
2.3 结构振动分析
以车速160 km/h,减振垫刚度0.019 N/mm3工况为例,从时域和频域两方面对城际铁路橡胶浮置板轨道的结构振动进行分析。轨道结构各部分垂向加速度时程曲线和频谱曲线分别如图5、图6所示。
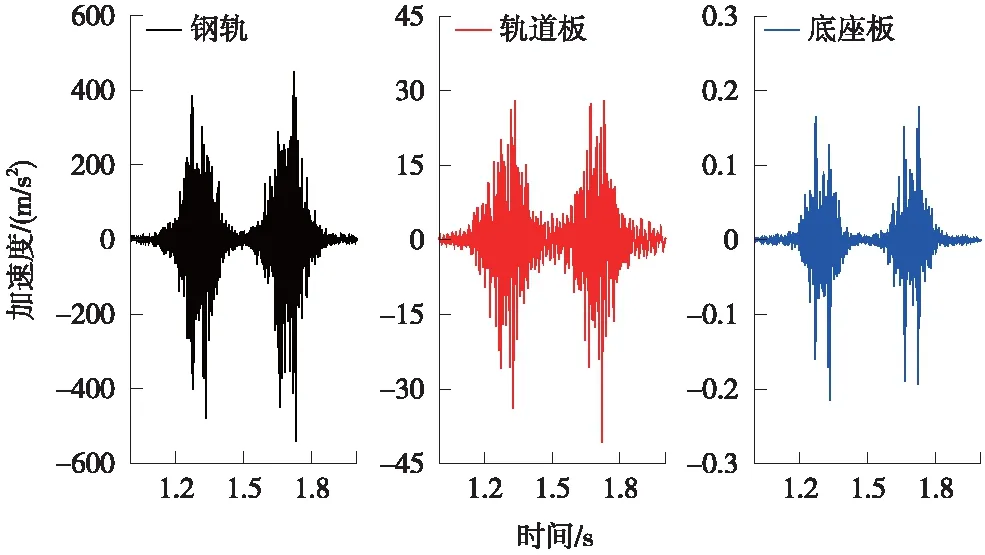
图5 钢轨、轨道板、底座板加速度时程曲线
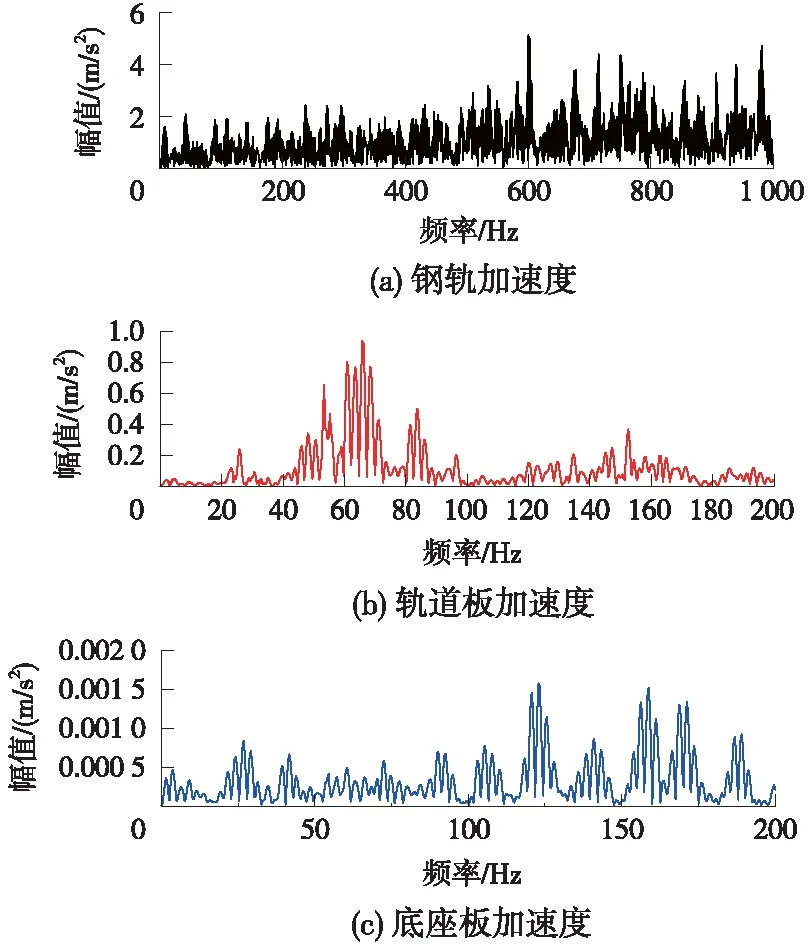
图6 钢轨、轨道板、底座板加速度频谱
根据图5可知,钢轨、轨道板、底座板加速度在一节车通过时出现2次峰值,钢轨、轨道板、底座板加速度峰值依次为542.61,40.81,0.22 m/s2。由轨道板到底座板,结构振动减小明显,说明橡胶浮置板轨道结构在时域上减振效果明显。
进一步分析轨道各位置频谱,如图6所示,行车荷载激励下,车轮与钢轨相互作用剧烈,钢轨处产生的振动为高频振动,频域峰值出现在600 Hz附近。振动传递到轨道板时,200 Hz以下频率振动占主导,轨道板主频峰值出现在64 Hz附近,与轨道结构固有属性有关。振动经橡胶减振垫传递到底座板时再次衰减,有效降低了64 Hz附近频域峰值,底座板频谱最大幅值仅为轨道板的1/60。
3 振动特性影响因素分析
3.1 行车速度影响
为确定不同设计速度对城际铁路橡胶浮置板轨道动力特性与减振效果影响,计算列车分别以速度120,160,200 km/h运营时,轨道结构各部分加速度峰值统计见表4。由表4可见,随着行车速度提高,轨道结构各部分加速度峰值均有所增大。列车速度由120 km/h到160 km/h,钢轨、轨道板、底座板加速度增幅分别为22.8%、18.9%、31.8%;由160 km/h到200 km/h,钢轨、轨道板、底座板垂向加速度增幅分别为28.2%、7.0%、47.6%。
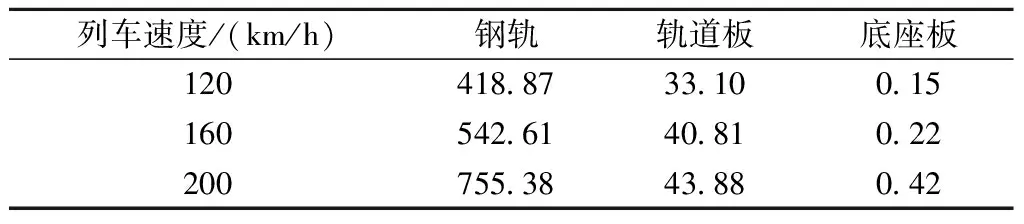
表4 轨道结构各部分垂向加速度峰值统计 m/s2
进一步分析不同设计速度下底座板垂向加速度1/3倍频程分频振级,并计算速度120 km/h与200 km/h振级之差,如图7所示。
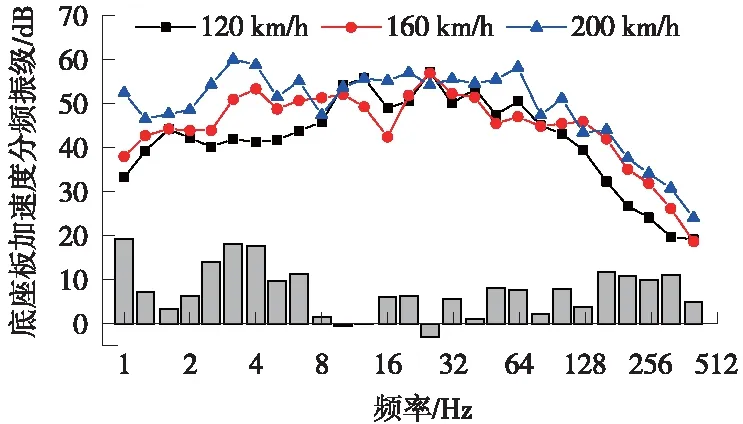
图7 底座板垂向加速度分频振级
由图7可知,随着列车运行速度的提高,底座板1~8 Hz及80 Hz以上振动均有所增加,最大差值可达19.2 dB。由于8~80 Hz处于橡胶浮置板基频影响频段内,底座振动与车速相关性小,因此,不同速度下振级相差较小。当列车运行速度为120,160,200 km/h时,底座板垂向加速度Z振级[20]分别为63.2,63.5,68.2 dB,120 km/h和200 km/h车速下底座板振级之差为5 dB。说明轨道结构振动随车速增加而增大,而城际铁路相比于城市轨道交通运营速度较高,因此,在减振地段,有必要采用减振效果更优的橡胶浮置板轨道。
3.2 减振垫刚度影响
减振垫刚度是影响减振效果以及轨道结构动力响应的关键参数,为分析减振垫刚度对轨道动力特性的影响规律,计算不同减振垫刚度下轨道各位置的振动响应,振动加速度峰值见表5。其中,底座板加速度时程曲线如图8所示。
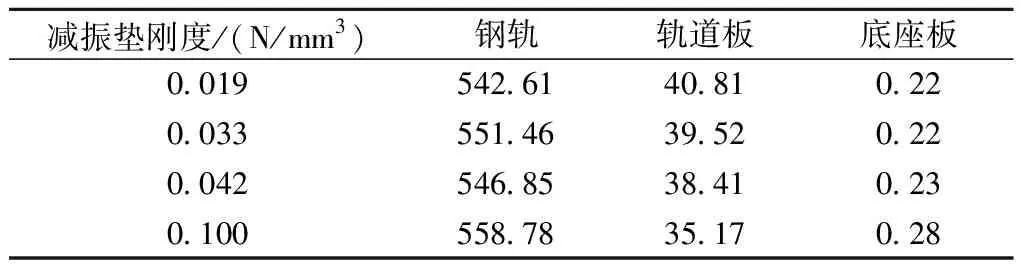
表5 不同减振垫刚度下轨道结构加速度峰值统计 m/s2
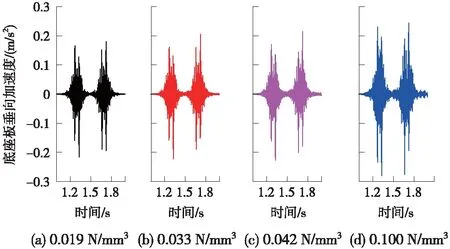
图8 不同减振垫刚度下底座板加速度时程曲线
由图8可见,随减振垫刚度由0.019 N/mm3增加至0.1 N/mm3时,钢轨加速度有降低趋势,轨道板加速度明显降低。底座板加速度随着减振垫刚度增大逐渐增大,减振垫刚度从0.019 N/mm3增大到0.1 N/mm3,底座板振动加速度峰峰值从0.22 m/s2增大至0.28 m/s2。说明减振垫刚度越小,越有利于底座及环境振动的控制,因此,采用刚度较小的减振垫可以提高橡胶浮置板轨道的减振效果。
计算不同减振垫刚度下底座板加速度分频振级如图9所示。对比可知,64 Hz频率的相应振级在减振垫刚度增大时明显增加,减振垫刚度0.1 N/mm3工况下50~80 Hz振动均有明显增大;在其他频域范围内,对于不同垫层刚度工况,分频振级基本一致,在10 Hz以下分频振级甚至略有减小。
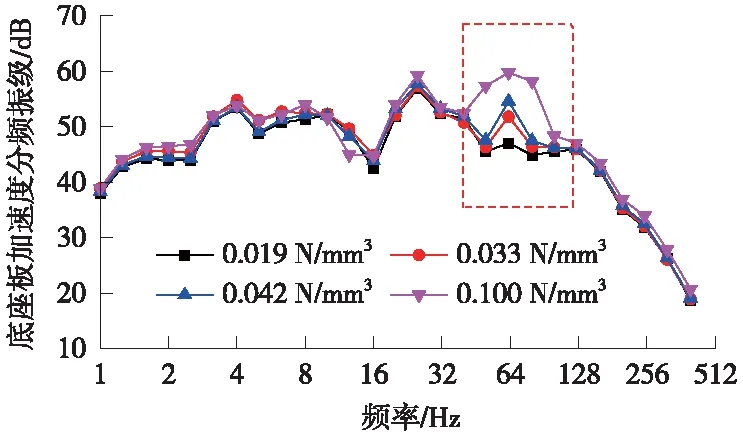
图9 不同减振垫刚度下底座板垂向加速度分频振级
4 落轴试验验证
4.1 试验平台及测点布置
为进一步研究橡胶浮置板轨道的动力响应特性及减振效果,开展足尺模型落轴冲击试验[21]。建立的橡胶浮置板轨道试验平台如图10所示,试验平台由6块轨道板组成,长30 m。测试指标为轨道各结构的加速度以及钢轨垂向力。钢轨加速度测点设置在钢轨轨底上表面,轨道板加速度测点设置于轨道板表面,底座加速度测点设置在离轨道中心线一定距离的底座板上。钢轨、轨道板、底座板加速度测点设置于同一截面,钢轨垂向力测点在轨腰处。各测点布置如图11所示。

图10 板式减振轨道厂内试验平台
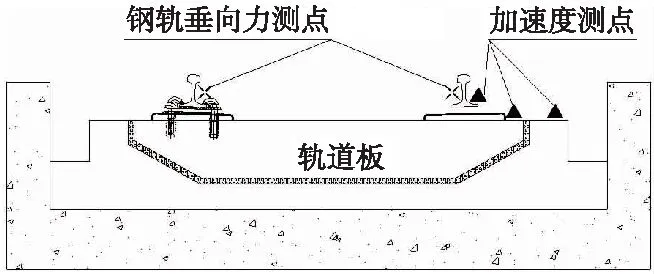
图11 落轴试验测点布置
4.2 试验结果分析
落轴高度的选择与车辆质量系数、车轮扁疤、车轮半径等参数有关[22]。根据《铁路技术管理规程》,假设列车车轮存在30 mm扁疤,可计算得出落轴高度为19.76 mm≈20 mm,因此,取落轴高度20 mm作为基本工况,在该落轴高度下,测试设置橡胶减振垫(垫层刚度0.019 N/mm3)、不设置橡胶减振垫2种工况下动态响应。同时,考虑到落轴高度在10~30 mm范围内的轮轨冲击力也在实测轮轨力峰值的范围内[23],因此,增加10 mm和30 mm落轴高度进行对比试验。
图12为20 mm落轴高度工况下橡胶浮置板轨道结构动态响应时程曲线,可以看出,轮轨力、钢轨加速度、轨道板加速度均出现明显冲击峰值,钢轨垂向力峰值136 kN,钢轨加速度128.3g,轨道板、底座板加速度峰值分别为1.60g、0.72g。
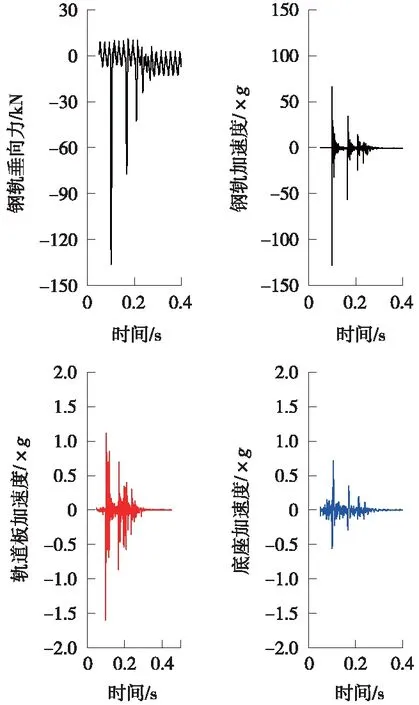
图12 20 mm落轴高度轨道结构动态响应时程曲线
进一步分析橡胶浮置板轨道各部分振动的频域分布,与不设置橡胶减振垫时的底座振动进行对比。图13所示为落轴高度20 mm工况轨道各部分振动1/3倍频程Z振级,其中,无减振垫工况仅提取底座板分频振级以方便对比。由图13可知,结构振动由钢轨、轨道板至底座逐渐衰减,各频段振动均有所减小,10 Hz附近振动衰减最慢。
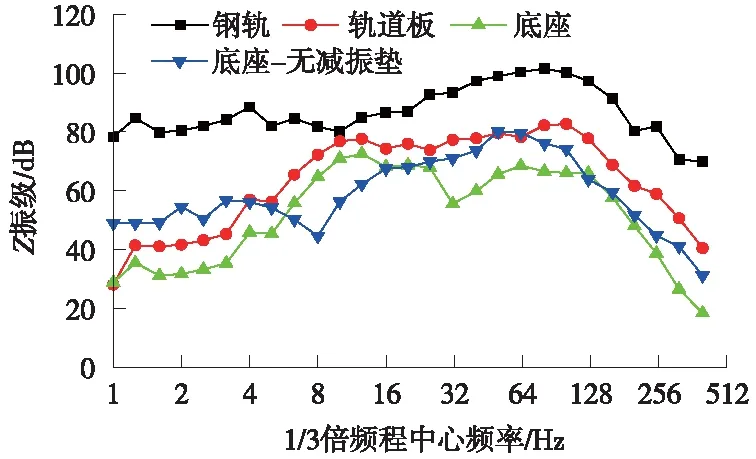
图13 落轴冲击下轨道结构各部分1/3倍频程分频振级
对比有、无橡胶减振垫工况的底座板振动,有橡胶垫时底座板振动在6~16 Hz范围内大于无橡胶垫工况,其他频域范围内均小于无橡胶垫工况,尤其在32~100 Hz频段内减振效果明显。分析其原因,橡胶浮置板轨道控制轨道振动是通过减振垫隔离高频振动,故在基频附近频域区段减振效果良好,而对低频振动过滤效果不明显。
由于落轴试验为瞬时冲击试验,轨道响应离散性大,统计不同工况多次试验得到的轨道结构加速度响应峰值及振级最大值、平均值,如表6所示。
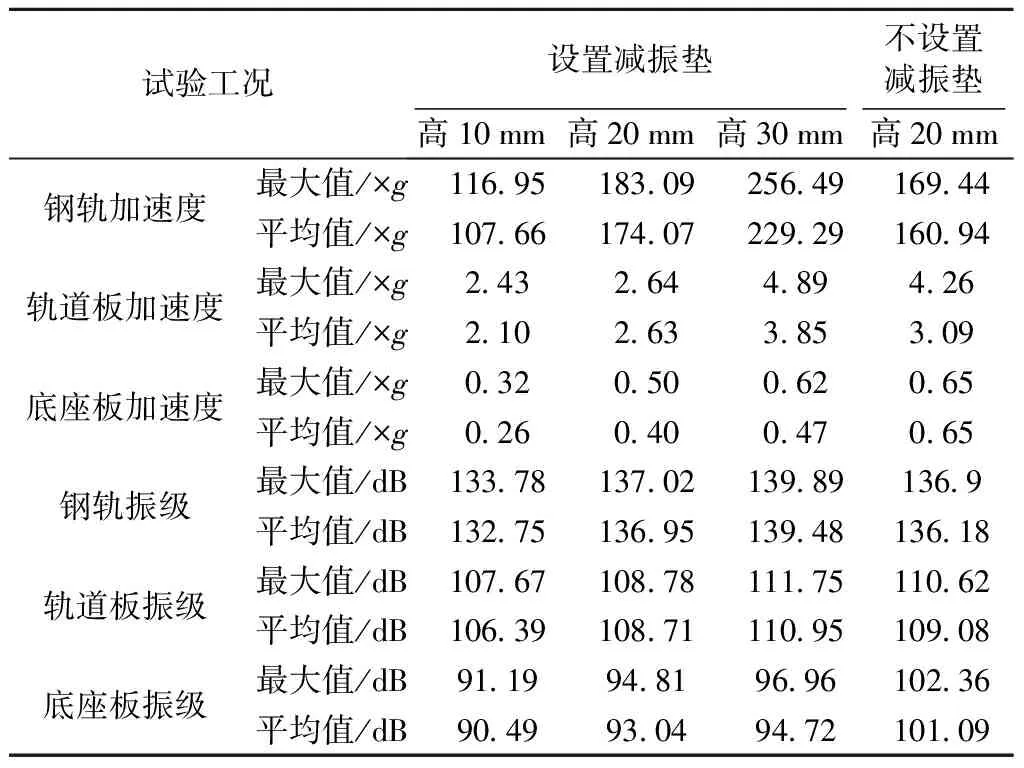
表6 不同工况下轨道结构加速度响应峰值及振级统计
根据表6可知,对于设置减振垫工况,随着落轴高度增大,激振作用力增大,钢轨、轨道板、底座的振动加速度及振级逐渐增大。落轴高度从10 mm依次增大到20,30 mm,钢轨加速度平均值增大61.7%、113.0%,轨道板加速度平均值增大25.2%、83.3%,底座最大加速度平均值增大53.8%、80.8%。从振级角度看,从钢轨到轨道板再到底座板,振动分别减小约28,15 dB,且平均振级随落轴高度略有增大。对于落轴高度20 mm工况,相比于无减振垫,有减振垫工况钢轨加速度略有增大,而轨道板和底座加速度明显减小,底座加速度平均值减小38.5%。从振级角度分析,钢轨、轨道板振级相当,而底座振级降低8 dB,说明橡胶浮置板轨道具有良好减振效果。
5 结论
从理论及试验角度对橡胶浮置板轨道动力特性进行了研究,主要结论如下。
(1)城际铁路橡胶浮置板轨道各动力指标能够满足要求,轨道振动基频为64 Hz左右,与车速、线路不平顺、轨道结构有关。
(2)随着减振垫刚度增大,底座板64 Hz处振动峰值增大明显。橡胶浮置板轨道可有效降低底座板以下结构振动,减振垫刚度建议取0.019~0.042 N/mm3。
(3)轨道振动随车速提高呈线性增大,1~8 Hz及80 Hz以上频段对车速敏感,速度由120 km/h增至200 km/h时,底座板总振级提高5 dB,而橡胶浮置板基频影响频段(8~80 Hz)的分频振级相差较小。
(4)通过落轴试验测试,橡胶浮置板轨道在32~100 Hz频段内减振效果明显,设置橡胶垫可降低底座板总振级8 dB。
本研究可为城际铁路橡胶浮置板轨道研究及设计提供理论指导。
